采用自适应无迹卡尔曼滤波器的车速和路面附着系数估计

张家旭,李静

(1.吉林大学汽车仿真与控制国家重点实验室,130022,长春;2.中国第一汽车集团技术中心,130011,长春)



采用自适应无迹卡尔曼滤波器的车速和路面附着系数估计

张家旭1,2,李静1

(1.吉林大学汽车仿真与控制国家重点实验室,130022,长春;2.中国第一汽车集团技术中心,130011,长春)

针对车辆主动安全控制中的车速和路面附着系数这一关键信息,提出了一种实时估计该信息的滤波算法,同时建立了将包含时变噪声统计特性的七自由度非线性车辆动力学模型作为滤波算法的标称模型,以及一种自适应无迹卡尔曼滤波算法。该算法采用传统的无迹卡尔曼滤波器来估计车速和路面附着系数,同时利用次优Sage-Husa噪声估计器对系统的噪声统计特性进行实时更新,其中采用遗忘因子限制噪声估计器的记忆长度,使新近数据发挥重要作用,使陈旧数据逐渐被遗忘,从而解决了因系统标称模型误差、外界扰动等因素引起的噪声时变的问题。在不同路面条件下进行了多种工况的实验验证,并与无迹卡尔曼滤波器的估计结果进行对比分析,结果表明,该算法具有良好的鲁棒性,其估计精度高于无迹卡尔曼滤波器,且满足车辆主动安全控制系统的要求。

车辆动力学;自适应滤波;无迹卡尔曼滤波;次优Sage-Husa噪声估计器

准确实时获取车辆的行驶状态与路面附着条件是实现车辆主动安全控制的必要前提,而这些信息通常无法直接测量,由此衍生出的基于车载传感器获得的车辆状态信息进行汽车状态参数估计成为近年来研究的热点[1-5]。

文献[6]基于滚动时域算法估计了车速和路面附着系数,文献[7]应用无迹卡尔曼滤波器(unscented Kalman filter, UKF)对汽车状态进行了估计,文献[8]采用扩展卡尔曼滤波器(extended Kalman filter, EKF)对汽车纵向车速和侧向车速进行了估计,文献[9]采用交互式多模型算法估计了车速和路面附着系数。

UKF与传统EKF相比,具有估计精度高和实时性强的特点[10],但二者均需要较精确的系数数学模型与噪声统计特性,否则会导致预测和滤波精度降低,甚至产生滤波发散的现象。为此,本文通过将UKF与次优Sage-Husa噪声估计器结合形成了一种自适应无迹卡尔曼滤波器(adaptive unscented Kalman filter, AUKF)算法,并在利用UKF估计车速和路面附着系数的同时,采用次优Sage-Husa噪声估计器同步估计系统的过程噪声。

1 车辆动力学模型

本文采用了如图1所示的七自由度车辆动力学模型作为车速和路面附着系数估计算法设计的标称模型,该模型包括车辆的纵向、侧向、横摆3个方向的运动以及4个车轮的回转运动。

图1 七自由度车辆动力学模型示意图

对于图1所示的模型,规定了车辆的车体坐标系:车辆的质心为车体坐标系原点;x轴为车辆纵向对称轴,向前为正;y轴通过质心,向左为正;所有回转角和水平面内力矩以逆时针方向为正,所有的矢量与坐标轴同向为正。基于此,建立车辆运动的微分方程如下。

纵向运动

(1)

Fx3+Fx4]

(2)

式中:vx为纵向速度;vy为侧向速度;ax为纵向加速度;m为整车质量;α为前轮转角;Fy1、Fy2分别为2个前轮上的侧向力;Fx1、Fx2、Fx3、Fx4分别为4个车轮上的纵向力。

侧向运动

(3)

Fy3+Fy4]

(4)

式中:ay为侧向加速度;Fy3、Fy4分别为2个后轮上的侧向力。

横摆运动

(5)

式中:r为横摆角速度;Iz为整车绕垂直轴的转动惯量;tf、tr分别为前轮距宽和后轮距宽;A、B分别为整车质心到前轴和后轴的距离。

为描述轮胎所受的纵向力Fxi和侧向力Fyi,i=[1,2,3,4],引入修正的Dugoff轮胎模型,其Fxi和Fyi分别表示为

(6)

(7)

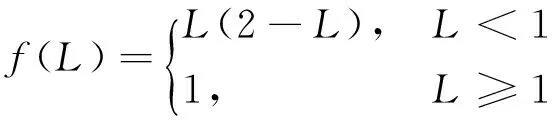
(8)

(9)

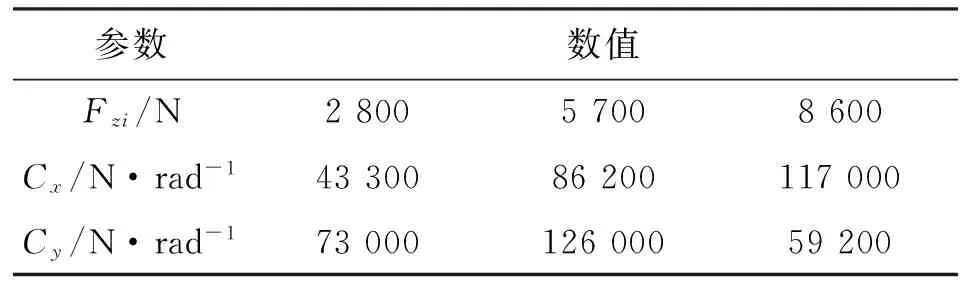
式中:μ为路面附着系数;Fzi为轮胎垂向载荷;λi为轮胎纵向滑移率;Cx为轮胎纵向刚度;Cy为轮胎侧偏刚度;βi为轮胎侧偏角;ε为速度影响因子。

修正的Dugoff轮胎模型的输入参数Fzi、βi和λi可以表示为参量α、vx、vy、ax、ay的函数形式,详见文献[11]。

根据车载传感器测量得到的ax、ay、r、α和轮速[w1w2w3w4]T,估计车辆的vx、vy、r、μ,其中将r作为被估计状态是为了充分利用测量信息,将μ作为被估计状态是为了使算法设计的标称模型适应不同的路面条件。因此,根据图1所示七自由度车辆动力学模型,设状态向量为x=[vxvyrμ]T,系统输入为u=[δw1w2w3w4]T,观测向量为y=[axayr]T。这样,由式(1)～(9)可得车辆系统的连续状态方程和观测方程为

(10)

定义采样时间为T,且在采样时间间隔内系统输入u保持不变。对式(10)的连续状态方程进行泰勒展开得

(11)

式中:k表示第k个采样时刻。

考虑系统的状态噪声和观测噪声,同时采用前向欧拉算法简化式(11)的运算(N=1),得到车辆系统的离散化状态方程和观测方程为

(12)

式中:wk、vk为相互独立的白噪声。其中,噪声统计特性为

E[wk]=qk

E[vk]=rk

E{[wk-qk][wj-qk]T}=Qkδkj

E{[vk-rk][vj-rk]T}=Rkδkj

式中:qk、Qk为过程噪声的均值和协方差阵;rk、Rk为观测噪声的均值和协方差阵;δkj为克罗内克函数。

2 自适应AUKF算法

本文在估计车速和路面附着系数时,采用次优Sage-Husa噪声估计器对系统过程噪声的均值和协方差阵进行实时估计,同时根据车载传感器的特性预先校准观测噪声的均值和协方差阵。将次优Sage-Husa噪声估计器引入到UKF算法[12]中得到的AUKF算法的设计步骤如下。

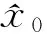
(13)

(14)

χi,k|k=

(15)

式中:(((n+ξ)Pk|k)1/2)i为矩阵平方根第i列[13]。

(16)

(17)

(18)

式中:ξ=τ2(n+κ)-n,为尺度调节因子;τ为尺度参数,决定Sigma点的分散度,通常取为较小的正值,本文取τ=0.01;κ为次级尺度调节因子,对于状态估计通常设定为0;γ为包含先验分布的高阶矩知识,对于高斯分布,γ=2最优。

步骤3时间更新过程为

(19)

(20)

Pk+1|k=

(21)

φi,k+1|k=h(χi,k+1|k)+r

(22)

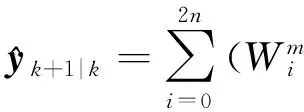
(23)

步骤4量测更新过程为

Pyk+1yk+1=

(24)

Pxk+1yk+1=

(25)

(26)

(27)

(28)

步骤5过程噪声统计特性更新过程为[14]

(29)

(30)

(31)

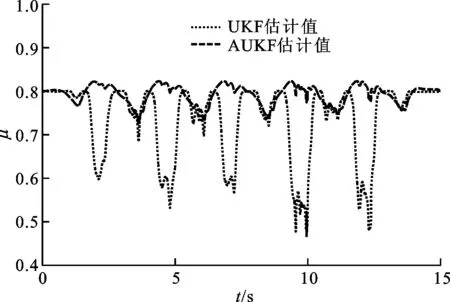
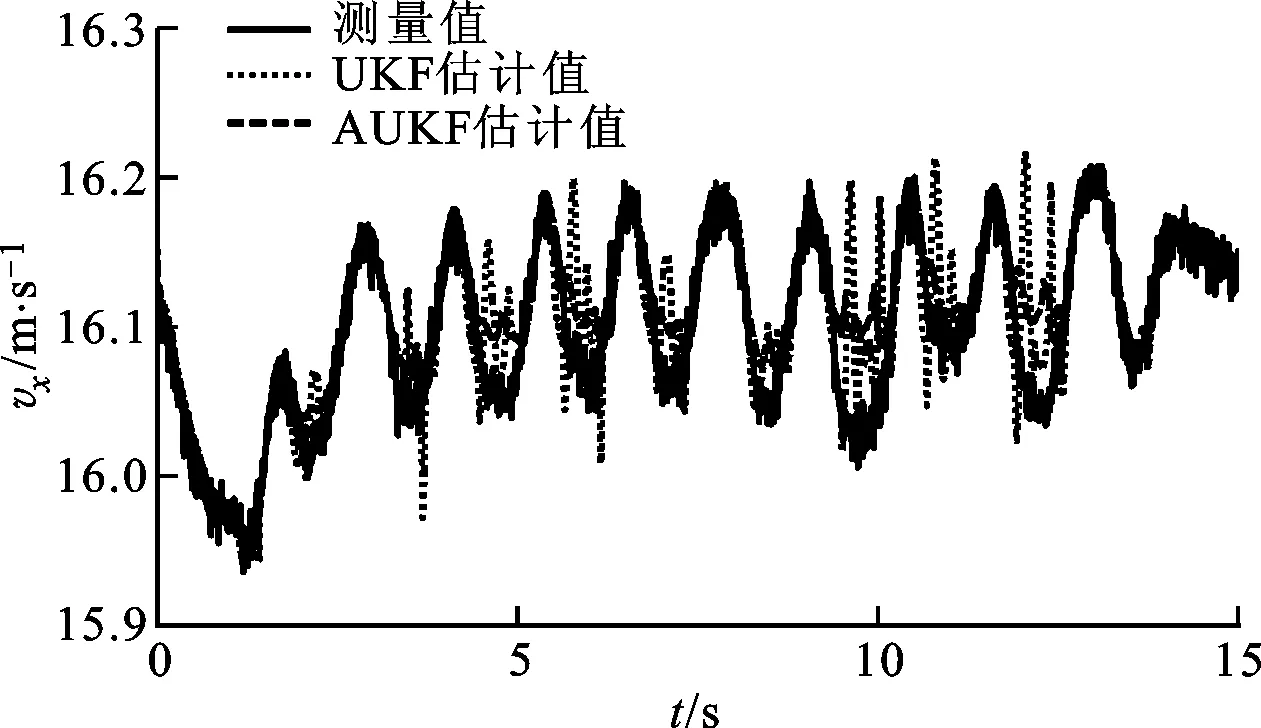
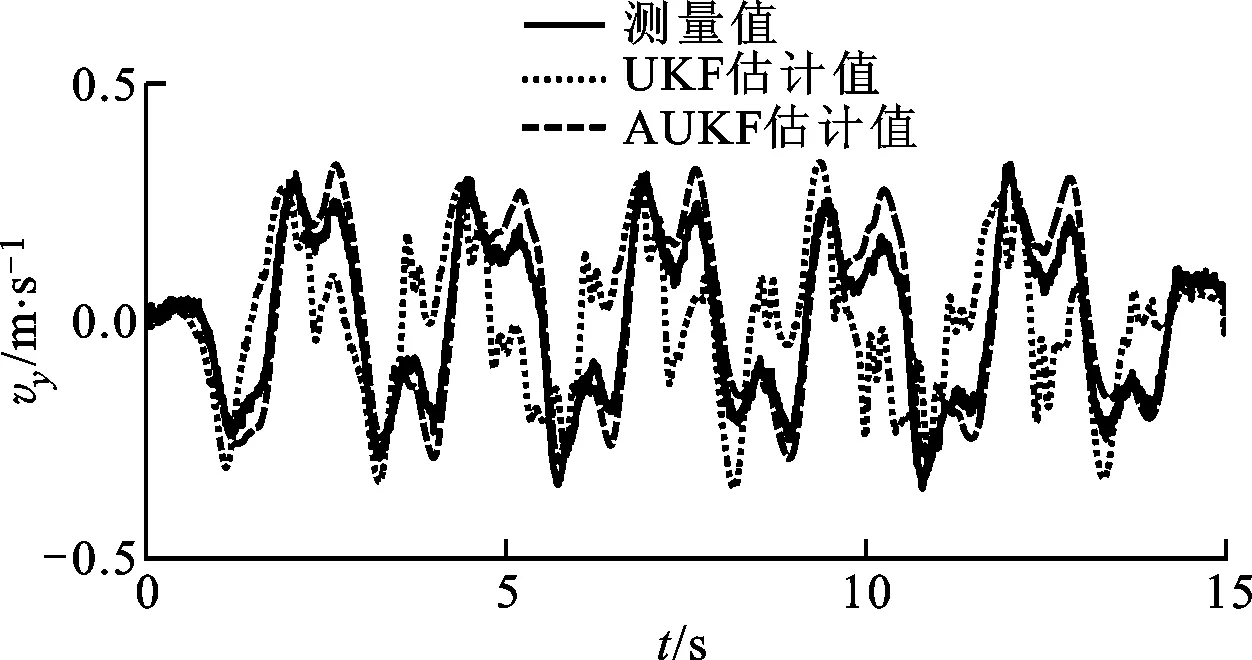
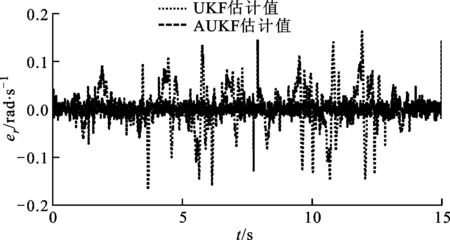
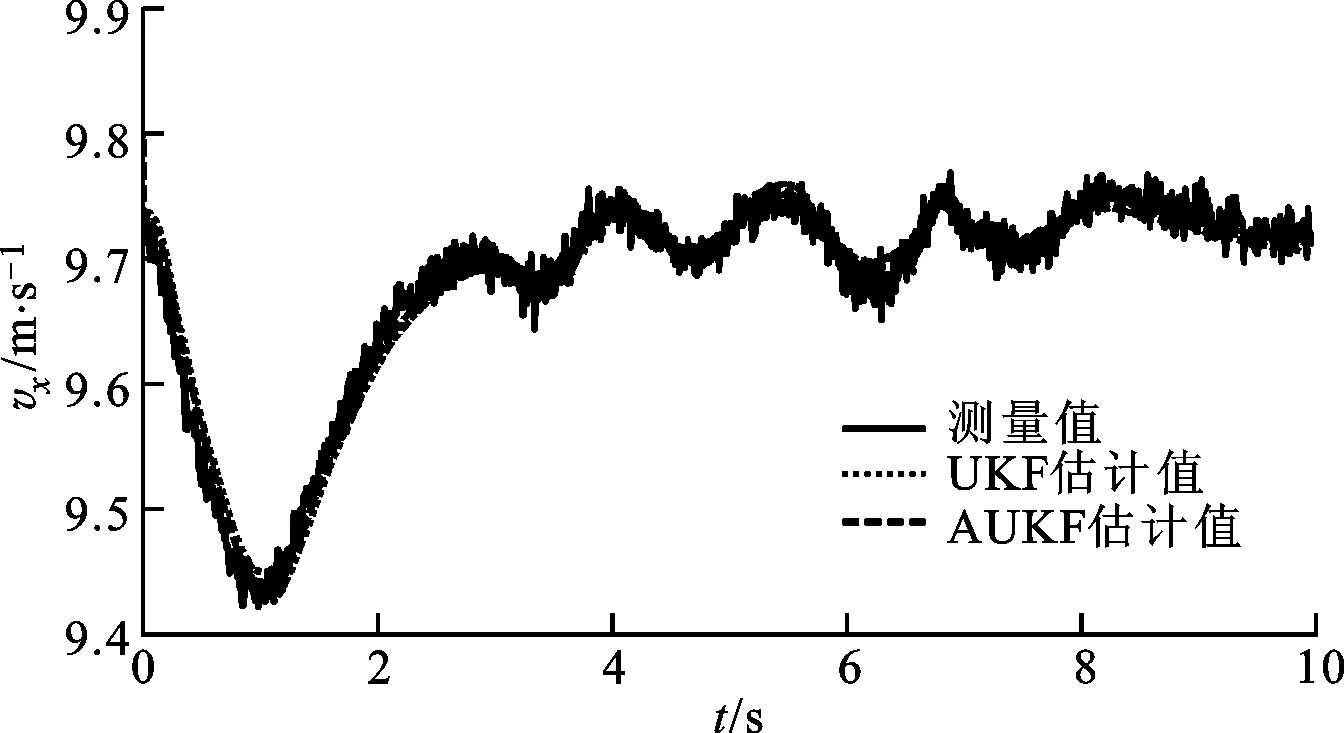
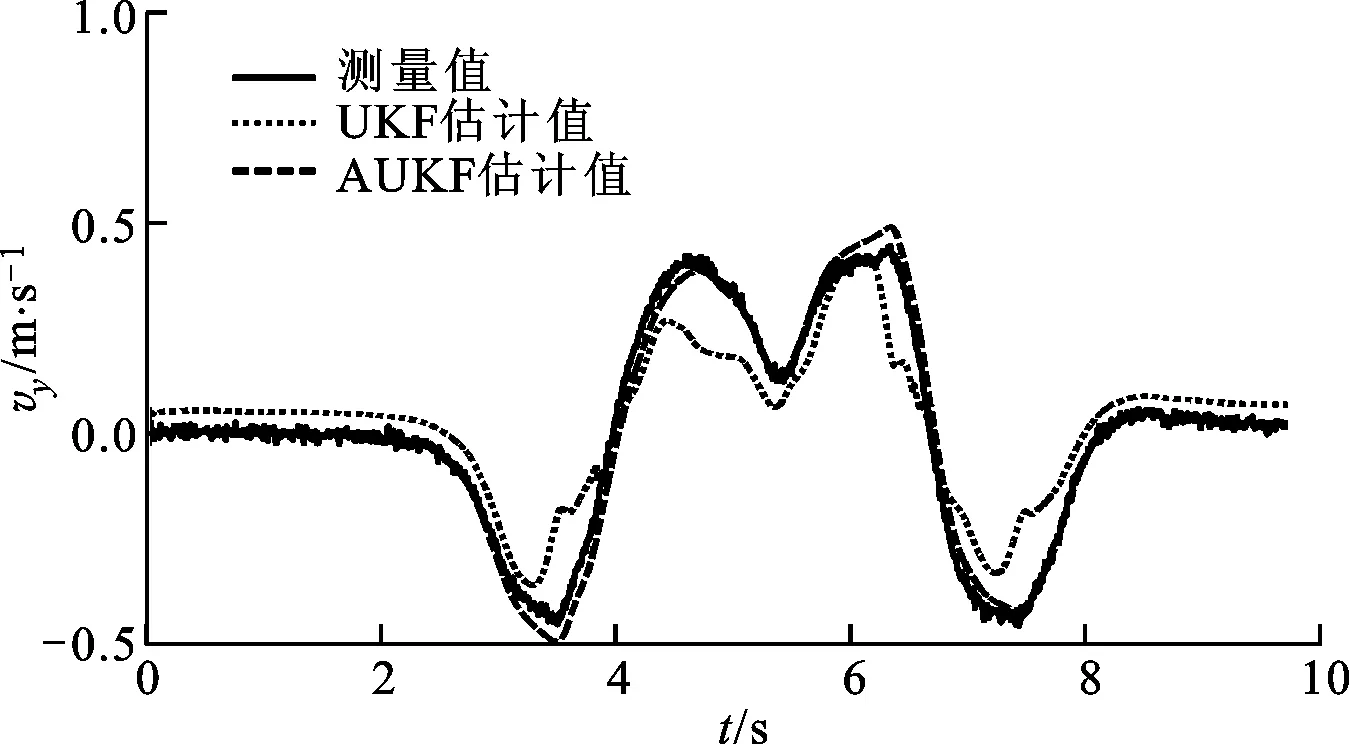
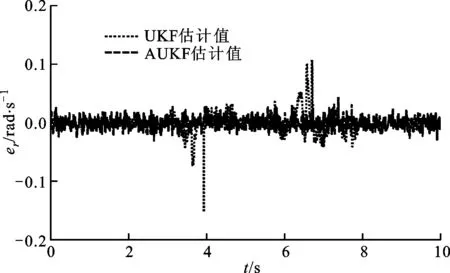
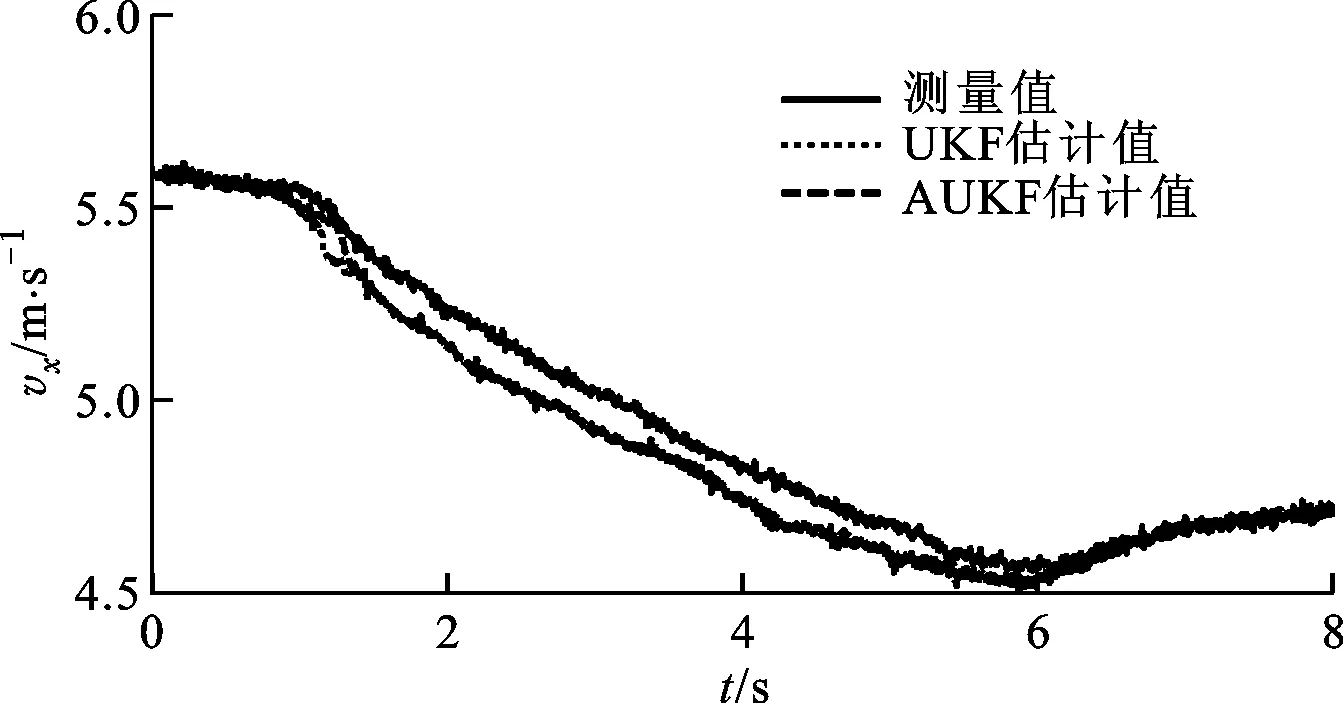
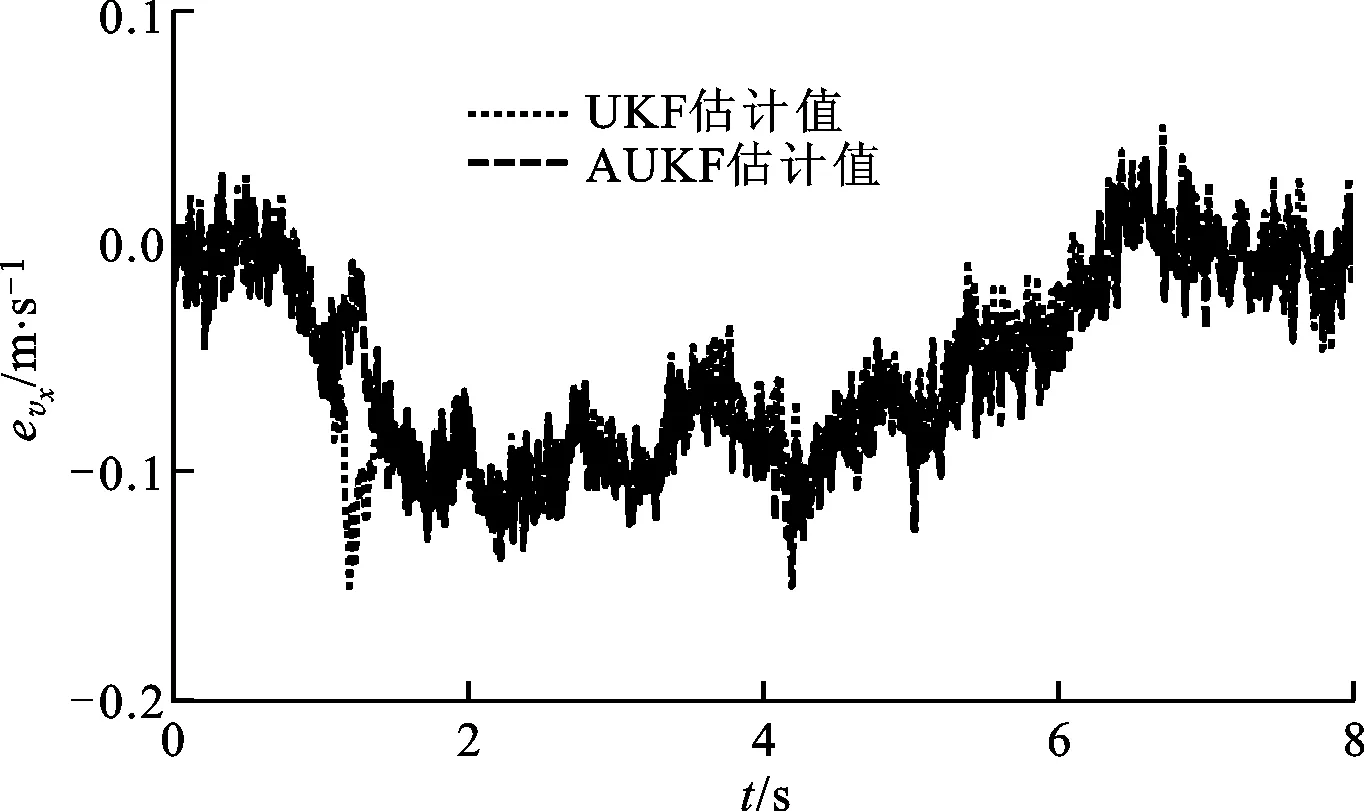
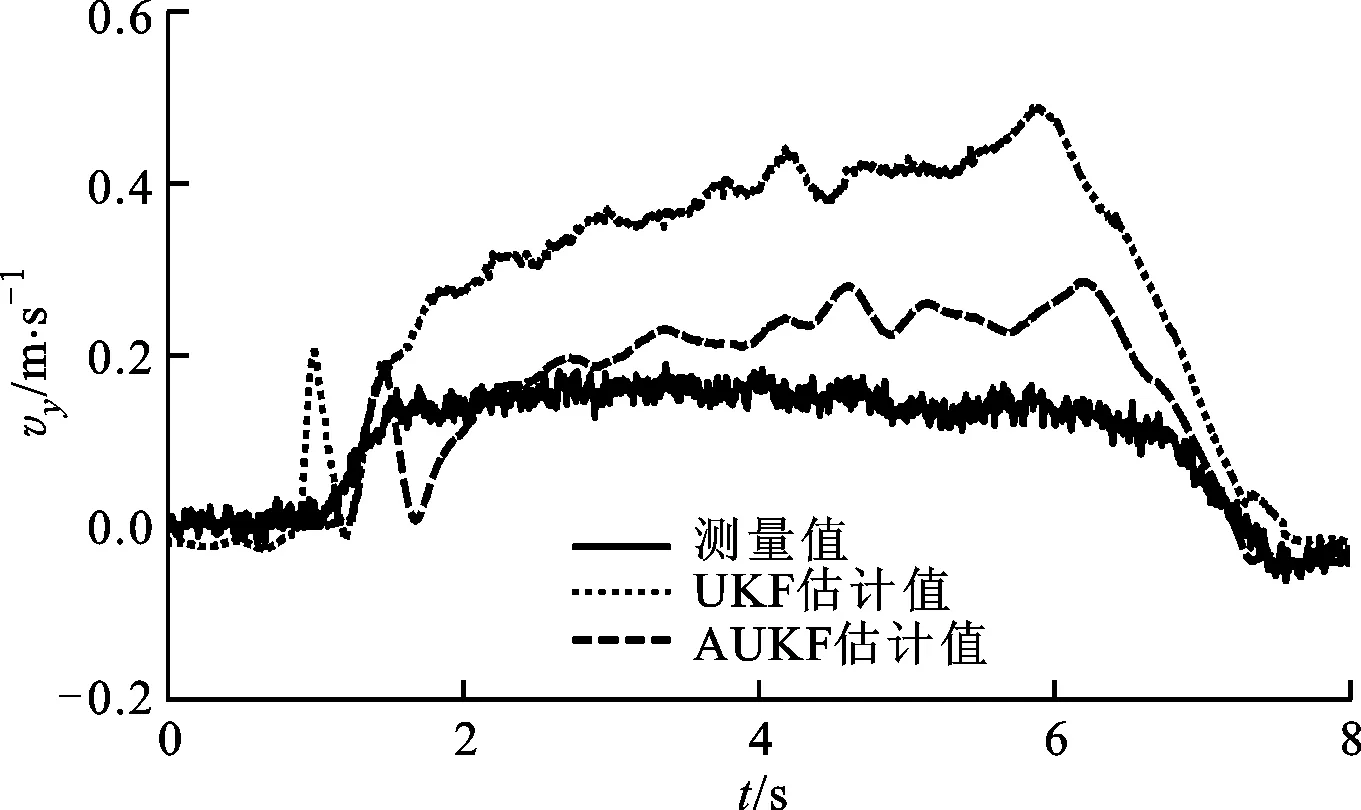
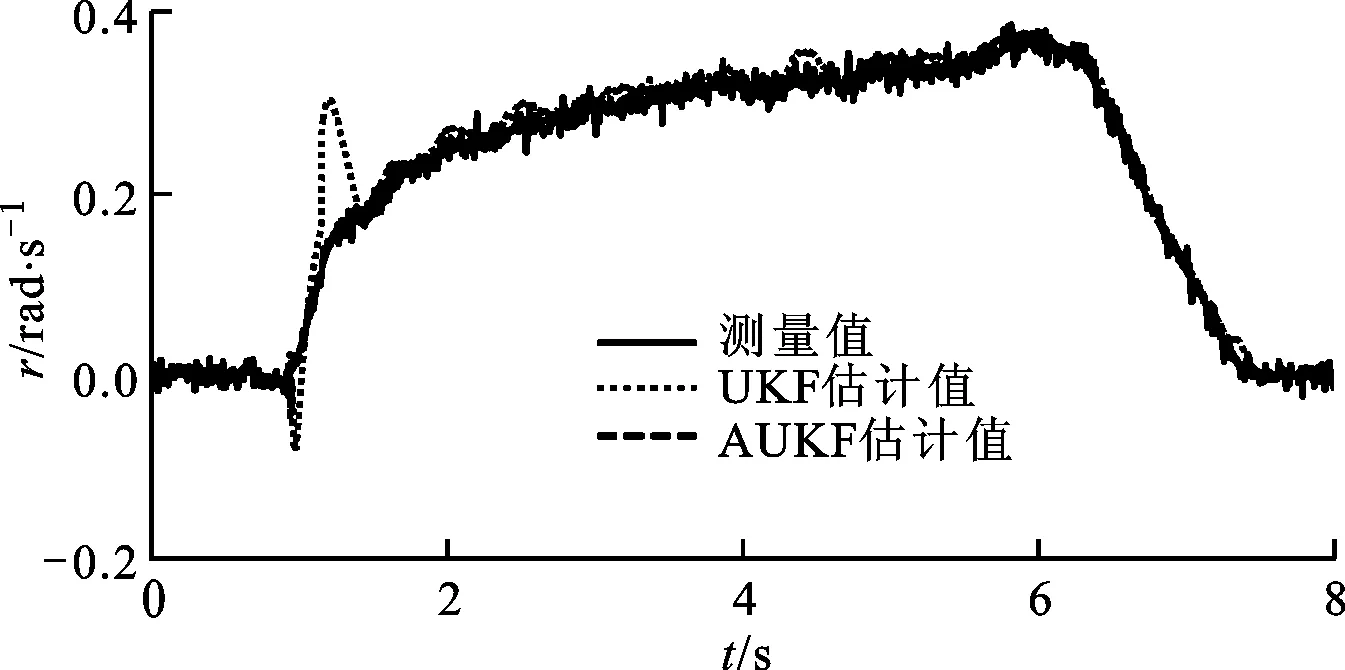
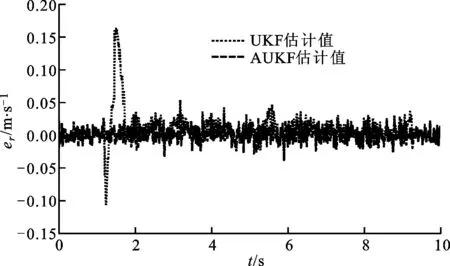
式中:c为遗忘因子,通常取0.95

采用遗忘因子可以限制滤波器的记忆长度,加重新近观测数据对现时估计的作用,使得新近数据在估计中发挥重要作用,使陈旧数据逐渐被遗忘。

在系统标称模型的噪声统计特性与实际模型的噪声统计特性完全匹配的前提下,UKF算法稳定收敛,且系统状态的估计误差协方差Pk+1|k+1趋于一个极小值[15-17]。次优Sage-Husa噪声估计器可对系统的噪声统计特性进行有效跟踪,进而提高AUKF算法的收敛性和滤波精度。

3 实车试验验证

为验证AUKF算法对车速和路面附着系数估计的有效性,利用某三厢轿车在干沥青路面、压实积雪路面和冰路面进行场地试验,该车安装有轮速传感器、方向盘转角传感器、GPS/INS惯性组合导航系统RT3000和转向机器人等,数据采集仪的采样频率为1 000 Hz。车辆及试验数据处理流程分别如图2和图3所示。

图2 实际车辆

图3 试验数据处理流程

车辆的试验参数如表1所示,车辆轮胎模型的纵向刚度和侧偏刚度在不同垂直载荷下的取值如表2所示。

表1 车辆试验参数

表2 车辆轮胎模型参数

设定AUKF算法的估计初始值为

P=diag[1,1,1]

R=diag[0.017 5,0.016 4,0.043 6]

Q=diag[0.001,0.001,0.001]

q=[0,0,0]T;r=[0,0,0]T

其中,纵向速度、侧向速度和横摆角速度的估计初始值取为GPS/INS惯性组合导航系统RT3000记录的试验初始值,干沥青路面附着系数的估计初始值为0.8,压实积雪路面附着系数的估计初始值为0.46,冰路面附着系数的估计初始值为0.23。在Matlab/Simulink环境下实现AUKF算法,并通过离线仿真将实车试验数据与AUKF算法的估计结果进行了对比分析。

3.1 蛇行试验

在干沥青路面上,依据标准[18]进行蛇行试验。驾驶员保持车辆以58 km/h稳定速度蛇行通过试验路段,利用数据采集仪记录试验过程中车辆的行驶状态。其中,试验测量值、AUKF算法和UKF算法的估计结果以及2种算法估计结果的偏差e如图4～图10所示。结果表明:对于路面附着系数,AUKF算法和UKF算法的估计结果均随着车辆的转向波动,但UKF算法的估计结果波动较大;对于纵向速度和横摆角速度,2种算法均取得了较好的估计效果;对于侧向速度,AUKF算法的估计结果与试验测量值之间存在一定偏差,而UKF算法的估计结果与试验测量值之间的偏差较大。

图4 蛇行工况下的路面附着系数估计

图5 蛇行工况下的纵向速度估计

图6 蛇行工况下的纵向速度估计偏差

图7 蛇行工况下的侧向速度估计

图8 蛇行工况下的侧向速度估计偏差

图9 蛇行工况下的横摆角速度估计

图10 蛇行工况下的横摆角速度估计偏差

3.2 双移线试验

在压实积雪面上,依据标准[19]进行双移线试验。车辆初始速度为35 km/h,驾驶员保持加速踏板稳定,利用数据采集仪记录试验过程中车辆的行驶状态。其中,测量值、AUKF算法和UKF算法的估计结果以及2种算法估计结果的偏差如图11～图17所示。结果表明,对于路面附着系数,AUKF算法的估计结果较平稳,而UKF算法的估计结果存在较大的波动;AUKF算法对纵向速度、侧向速度和横摆角速度均取得了较好的估计效果,而UKF算法对纵向速度的估计结果与测量值之间存在一定的偏差。

图11 双移线工况下的路面附着系数估计

图12 双移线工况下的纵向速度估计

图13 双移线工况下的纵向速度估计偏差

图14 双移线工况下的侧向速度估计

图15 双移线工况下的侧向速度估计偏差

图16 双移线工况下的横摆角速度估计

图17 双移线工况下的横摆角速度估计偏差

3.3 J-Turn试验

在冰路面上,依据文献[20]进行了J-Turn试验。车辆直线行驶,初始车速为20 km/h,驾驶员松开加速踏板并且触发转向机器人,转向机器人以1 000 (°)/s的速度将方向盘转角增大到350°,并且保持4 s,然后用2 s的时间将方向盘转角以匀速回到0°。试验数据、AUKF算法和UKF算法的估计结果以及2种算法估计结果的偏差如图18～图24所示。结果表明:UKF算法对路面附着系数的估计结果随着车辆的转向动作有一定程度的波动,在车辆转向保持不动阶段AUKF算法与UKF算法估计的路面附着系数基本一致;对于纵向速度和侧向速度,2种算法的估计效果与测量值之间均存在一定的偏差,但UKF算法对侧向速度估计结果的偏差更大;对于横摆角速度,AUKF算法取得了较好的估计效果,而UKF算法的估计结果在J-Turn试验开始阶段出现波动。

图18 J-Turn工况下的路面附着系数估计

图19 J-Turn工况下的纵向速度估计

图20 J-Turn工况下的纵向速度估计偏差

图21 J-Turn工况下的侧向速度估计

图22 J-Turn工况下的侧向速度估计偏差

图23 J-Turn工况下的横摆角速度估计

图24 J-Turn工况下的横摆角速度估计偏差

对3种工况下UKF算法和AUKF算法的估计结果进行了定量分析,计算每个状态估计量的eMSE如表3所示。

3种试验工况下,在车辆快速转向过程中较大的车辆侧倾运动以及轮胎进入非线性工作区域会导致车辆参数摄动、增加模型误差。这些扰动可折算到系统的过程噪声中,相对于UKF算法,AUKF算法可实时估计系统过程噪声的均值和协方差,有效抑制扰动对车速和路面附着系数估计结果的影响,提高系统状态量的估计精度,增加系统的鲁棒性。

表3 状态估计量的均方误差

4 结 论

本文结合无迹卡尔曼滤波器与次优Sage-Husa噪声估计器,提出了一种自适应无迹卡尔曼滤波器算法,并采用该算法估计了车速和路面附着系数。经试验验证,得出如下结果。

(1)基于七自由度车辆动力学模型的AUKF算法可以较为准确地估计车辆纵向速度、侧向速度、横摆角速度和路面附着系数。特别是存在车辆参数摄动、模型误差时,该算法的估计精度依然较高,具有较强的鲁棒性。

(2)在同等条件下,AUKF算法的估计精度高于UKF算法,且简单、可靠、易于实现。通过对路面附着系数的估计表明,该算法能够适应不同的路面条件。

[1] 郭洪艳, 陈虹, 赵海燕, 等. 汽车行驶状态参数估计研究进展与展望 [J]. 控制理论与应用, 2013, 30(6): 661-672. GUO Hongyan, CHEN Hong, ZHAO Haiyan, et al. State and parameter estimation for running vehicle: recent developments and perspective [J]. Control Theory & Applications, 2013, 30(6): 661-672.

[2] AYYOUB R, REZA Z, SABER F, et al. Cascaded dual extend Kalman filter for combined vehicle state estimation and parameter identification, SAE 2013-01-0691 [R]. Washington, DC, USA: SAE, 2013.

[3] 林程, 周逢军, 徐志峰, 等. 基于补偿自适应控制算法的车辆状态参数估计 [J]. 农业机械学报, 2014, 45(11): 1-8. LIN Cheng, ZHOU Fengjun, XU Zhifeng, et al. Estimation of vehicle status parameters based on compensation adaptive control algorithm [J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(11): 1-8.

[4] XIAOSHUAI X, JINXI C, JIANXIAO Z. Vehicle state estimation using cubature Kalman filter [J]. International Journal of Vehicle Mechanics and Mobility, 2014, 49(9): 1497-1520.

[5] 包瑞新, 贾敏, EDOARDO S, 等. 基于扩展Kalman粒子滤波的汽车行驶状态和参数估计 [J]. 农业机械学报, 2015, 46(2): 301-306. BAO Ruixin, JIA Min, EDOARDO S, et al. Vehicle state and parameter estimation under driving situation based on extended Kalman particle filter method [J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(2): 301-306.

[6] 赵林辉, 刘志远, 陈虹. 车速和路面附着系数的滚动时域估计 [J]. 汽车工程, 2009, 32(6): 520-525. ZHAO Linhui, LIU Zhiyuan, CHEN Hong. The estimation of vehicle speed and tire-road adhesion coefficient using moving horizon strategy [J]. Automotive Engineering, 2009, 32(6): 520-525.

[7] ANTONOV S, FEHN A, KUGI A. Unscented Kalman filter for vehicle state estimation [J]. International Journal of Vehicle Mechanics and Mobility, 2011, 49(9): 1497-1520.

[8] HRGETIC M, DEUR J, IVANOVIC V, et al. Vehicle sideslip angle EKF estimator based on nonlinear vehicle dynamics model and stochastic tire forces modeling, SAE 2014-01-0144 [R]. Washington, DC, USA: SAE, 2014.

[9] TSUNASHIMA H, MURAKAMI M, MIATA J. Vehicle and road state estimation using interacting multiple model approach [J]. Vehicle System Dynamics, 2006, 44(S): 750-758.

[10]万莉, 刘焰春, 皮亦鸣. EKF、UKF、PF目标跟踪性能的比较 [J]. 雷达科学与技术, 2007, 5(1): 13-16. WAN Li, LIU Yanchun, PI Yiming. Comparing of target tracking performances of EKF, UKF and PF [J]. Radar Science and Technology, 2007, 5(1): 13-16.

[11]MASATO A. Vehicle handling dynamics theory and application [M]. Amsterdam, Netherlands: Elsevier, 2009.

[12]WAN E A, VANDER M R. The unscented Kalman filter for nonlinear estimation [C]∥Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing Communications, and Control Symposium. Piscataway, NJ, USA: IEEE, 2000: 153-158.

[13]JULIER S J, UHLMANN J K. Unscented filtering and nonlinear estimation [J]. Proceedings of the IEEE, 2004, 92(30): 401-422.

[14]SAGE A P, HUSA G W. Adaptive filtering with unknown prior statistics [C]∥Proceedings of Joint Automatic Control Conference. New York, USA: ASME, 1969: 760-769.

[15]XIONG K, ZHANG H Y, CHAN C W. Performance evaluation of UKF-based nonlinear filtering [J]. Automatica, 2006, 42(2): 261-270.

[16]WU Y X, HU D W, HU X P. Comments on performance evaluation of UKF-based nonlinear filtering [J]. Automatica, 2007, 43(3): 567-568.

[17]XIONG K, ZHANG H Y, CHAN C W. Author’s reply to “comments on ‘performance evaluation of UKF-Based nonlinear filtering’” [J]. Automatica, 2007, 43(3): 569-570.

[18]全国汽车标准化技术委员会. GB/T 6323.1—1994 汽车操纵稳定性试验方法: 蛇行试验 [S]. 北京: 中国标准出版社, 1994.

[19]British Standards Institution. ISO 3888-1—1999 Passenger cars-test track for a severe lane-change manoeuvre: part 1 Double-lane change [S]. New York, USA: American National Standards Institute, 1999.

[20]National Highway Traffic Safety Administration. A comprehensive experimental examination of test maneuvers that may induce on-road, untripped, light vehicle rollover-phase IV of NHTSA’s light vehicle rollover research program [R]. Washington, DC, USA: National Highway Traffic Safety Administration, 2002.

(编辑 苗凌)

Estimation of Vehicle Speed and Tire-Road Adhesion Coefficient by Adaptive Unscented Kalman Filter

ZHANG Jiaxu1,2,LI Jing1

(1. State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China;2. Research and Development Center, China FAW Group Corporation, Changchun 130011, China)

An adaptive unscented Kalman filter (AUKF) algorithm for estimating vehicle speed and tire-road adhesion coefficient, the essential information for the active safety systems, is proposed. 7-DoF nonlinear vehicle dynamics model containing varying statistical noise characteristics is established as the nominal model. To solve the effects from varying statistical noise characteristics on the estimation accuracy and stability, the proposed algorithm adopts the traditional unscented Kalman filter to estimate vehicle speed and tire-road adhesion coefficient, and the suboptimal Sage-Husa noise estimator is used to update the statistical noise characteristics of the system simultaneously, where the forgetting factor limits the memory length of noise estimator to enhance the role of the new data and to forget the old data gradually. In the real vehicle experiment environment, the performance of the proposed algorithm is verified and compared with that of unscented Kalman filter for a variety of maneuvers and road conditions. The tests indicate the better robustness and estimation accuracy of this AUKF algorithm, which meets the requirements of the active safety systems.

vehicle dynamics; adaptive filter; unscented Kalman filter; suboptimal Sage-Husa noise estimator

10.7652/xjtuxb201603011

2015-09-10。 作者简介:张家旭(1985—),男,博士生;李静(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51275206)。

时间:2015-12-10

http:∥www.cnki.net/kcms/detail/61.1069.T.20151210.1130.008.html

U461.1

:A

:0253-987X(2016)03-0068-08