广义逐次定数截尾下Pareto分布的统计分析

马永传，武 东，朱雅敏

(1.皖西学院 金融与数学学院，安徽 六安 237009；2.安徽农业大学 理学院，安徽 合肥 230036；3.华中科技大学 数学与统计学院，湖北 武汉 430074)



广义逐次定数截尾下Pareto分布的统计分析

马永传1，武 东2，朱雅敏3

(1.皖西学院 金融与数学学院，安徽 六安 237009；2.安徽农业大学 理学院，安徽 合肥 230036；3.华中科技大学 数学与统计学院，湖北 武汉 430074)

基于广义逐次定数截尾样本,对Pareto分布寿命产品进行贝叶斯统计分析,利用吉布斯抽样给出该模型的近似Bayes估计,最后通过模拟例子表明Bayes估计是有效的.

广义逐次定数截尾;Pareto分布;Bayes估计;吉布斯抽样

大量文献研究了经典的定时截尾和定数截尾及其统计分析[1]．Balakrishnan和Aggarwala(2000)将经典的定时截尾和定数截尾推广到广义逐次定时截尾和广义逐次定数截尾[2]．广义逐次定数截尾试验在可靠性分析中经常会遇见，拥有巨大价值，可广泛应用于医学、电子技术、机械和航空等领域．在Pareto分布产品的可靠性研究中，王亮等[3]提出了逐步首失效样本，并就Pareto分布进行了Bayes分析，侯华蕾等[4]考虑双边定数截尾寿命试验，该试验的优点就是允许左截尾和右截尾，主要利用Bayes方法对双边定数截尾下Pareto分布参数进行了估计．卫超等[5]研究了逐步增加II型截尾与定时截尾的融合称为逐步II型混合截尾，也对Pareto分布进行了Bayes分析．李凤[6-8]解决了逐步增加II型截尾下Pareto分布参数的逆矩估计、区间估计和Bayes估计．李琼等[9]也研究了逐步增加II型截尾下Pareto分布的Bayes估计，讨论参数先验两种方法：共轭先验与无信息先验法，并利用吉布斯抽样法解决Bayes计算问题．但以上均未对广义逐次定数截尾下Pareto分布的参数估计展开研究，本文就此问题进行讨论，主要分为3个部分：①给出广义逐次定数截尾下的模型进行描述 ；②解决广义逐次定数截尾下Pareto分布参数的最大似然估计；③讨论广义逐次定数截尾下Pareto分布参数的Bayes估计，结合吉布斯抽样法给出算法步骤；④利用Monte Carlo方法产生Pareto分布广义逐次定数截尾样本，并对Bayes估计与最大似然估计进行精度分析，结果表明Bayes估计有效而实用．

1 模型描述

广义逐次定数截尾试验是在定数截尾基础上的拓展，其模型描述和安排如下：首先依据随机原则选择n个测试产品进行试验，观察到第一个测试产品失效时刻xr+1:m:n时，已经有r个测试产品失效，然后从所剩的n-r-1个测试产品里随机移走Rr+1个产品，将余下的n-r-Rr+1-1个测试产品进行试验；观测到第二个测试产品失效时刻xr+1:m:n时，从所剩的n-r-Rr+1-2个测试产品里随机移走Rr+2个产品，将余下的n-r-Rr+1-Rr+2-2个测试产品进行试验；一直这样进行下去，直至观察到预定的m-r个测试产品失效时刻xm:m:n时结束试验．最后将所剩的Rm=n-r-Rr+1-Rr+2-…-Rm-1-(m-r-1)个测试产品移走．容易知道m-r个产品的失效时间为xr+1:m:n≤xr+2:m:n≤…≤xm:m:n.依据文献[2]知道似然函数如下：

(1)

2 最大似然估计

假设1 假设测试产品的寿命服从Pareto分布P(μ,α)，其概率密度和分布函数分别为

(2)

和

(3)

其中μ为分布的门限参数，α为分布的刻度参数．

设xr+1:m:n≤xr+2:m:n≤…≤xm:m:n是来自Pareto分布样本容量为n的广义逐次定数截尾样本，Rr+1,Rr+2,…,Rm-1,Rm是试验中依次被移开的产品个数．将(2)和(3)式代入(1)式，可得广义逐次定数截尾下Pareto分布的似然函数为

(4)

这里data={xr+i:m:n|i=1,2,…,m-r}．

于是，基于Pareto分布的广义逐次定数截尾样本的对数似然函数为

(5)

通过求解上述似然方程组，可得参数μ和α的最大似然估计分别为

和

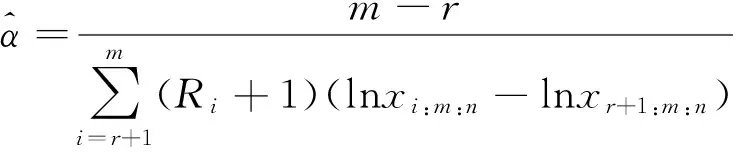
3 Bayes估计

从而得到参数μ的满条件后验密度为

而参数α的满条件后验密度为

下面采用吉布斯抽样(Gibbs Sampler)，对参数进行模拟和估计．它们随机数的产生都可以采用舍选抽样法．下面给出了广义逐次定数截尾下Pareto分布的Bayes估计的步骤：

Step1：选取参数(μ.α)的起始点(μ(0),α(0))，一般采用先验分布产生；

Step2：依据参数α的满条件后验密度π(α|μ(i-1))，并从中抽取随机数α(i)；

Step3：依据参数μ的满条件后验密度π(μ|α0(i))，并从中抽取随机数μ(i)；

Step4：令i=i+1，然后返回Step2，直至达到给定的迭代次数便结束迭代．

则α0(i)，μ(i)，i=1,2,…,N为参数(μ，α)的一个吉布斯迭代样本，通常将前N0(N>N0)个吉布斯迭代样本去掉，用剩余的N-N0个迭代样本的期望值作为参数(μ，α)的Bayes估计，即(μ,α)的Bayes估计分别为:

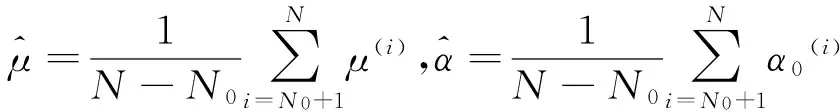
4 Monte Carlo模拟

以上对广义逐次定数截尾下Pareto分布进行了Bayes分析，利用Monte Carlo方法可得到该模型的随机数，具体步骤如下：

(1)从标准指数分布产生r+1个相互独立的随机数W1,W2,…,Wr+1；

(3)从标准指数分布产生m-r-1个相互独立的随机数Zr+2,Zr+3,…,Zm；

(4)令

i=2,3,…，m-r,则得到的广义逐次定数截尾下标准指数分布样本；其中n为试验的产品总个数，Rr+1,Rr+2,…,Rm-1为试验中依次被撤离的测试产品个数．

为了考察最大似然估计(MLE)与Bayes估计(Bayes)的精度，现取Pareto分布参数为α=1.5,σ=300，从该分布产生m-r个广义逐次定数截尾样本xr+1,xr+2,…,xm．每种方案产生100组模拟样本并分别计算估计的相对偏差与均方误差，这里Bayes估计迭代步数N=11000,舍弃迭代步数为N0=1000，迭代初始值为α=3,σ=200，具体试验安排与估计结果如表1所示．

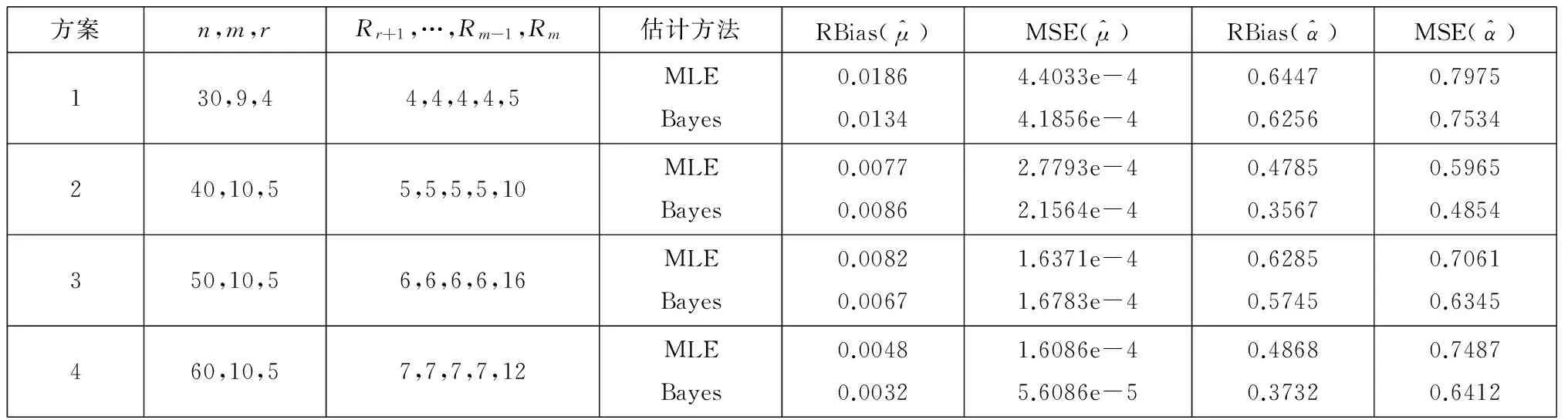
表1 广义逐次定数截尾下Pareto分布的试验方案与估计结果

从表1可以看出，该模型Bayes估计的精度较高，说明估计更加有效．

5 结语

利用吉布斯抽样法获得了广义逐次定数截尾下Pareto分布场合的一种近似Bayes估计．关于先验分布的选取，Pareto分布的门限参数和形状参数的先验取为无信息先验分布，而吉布斯抽样迭代过程的随机数产生采用了舍选抽样法．在基于吉布斯抽样法的Bayes计算过程，需要产生大量随机数，这样会造成计算效率低下,可考虑采用基于Lindley公式的积分近似法计算后验期望．

[1]茆诗松,汤银才,王玲玲.可靠性统计[M].北京:高等教育出版社,2008.

[2]BALAKRISHNAN N,AGGARWALA R.Progressive censoring:Theory,methods and applications[M].Boston: Birkhguser,2000.

[3]王亮,师义民,孙天宇.两参数Pareto分布逐步首失效样本的Bayes估计[J].系统工程理论与实践,2012,32(11): 2498-2503.

[4]侯华蕾,师义民,李豪亮.双边定数截尾下Pareto分布的可靠性分析[J].数理统计与管理,2009,28(5):826-830.

[5]卫超,师义民.逐步II型混合截尾下Pareto分布的统计分析[J].火力与指挥控制,2014,39(4):27-30.

[6]李凤.逐次定数截尾下Pareto分布参数的逆矩估计[J].统计与决策,2010(24):156-157.

[7]李凤.逐步增加II型截尾下Pareto分布参数的区间估计[J]. 科学技术与工程,2011,11(11):2554-2557.

[8]李凤,师义民.逐步增加II型截尾下Pareto分布的Bayes估计[J].数学的实践与认识,42(13):137-142.

[9]李琼,武东.逐步增加定数截尾下Pareto分布的贝叶斯分析[J].上海第二工业大学学报,2012,29(2):135-138.

(责任编辑:陈衍峰)

2016-05-06

国家自然科学基金项目“面板数据的最优设计”(11401056)

马永传,安徽六安人,副教授；武东,安徽六安人,副教授；朱雅敏,女,安徽安庆人．

O213.2

A

1008-7974(2016)05-0022-03

10.13877/j.cnki.cn22-1284.2016.10.007