电影首映日后票房预测模型研究

罗晓芃，齐佳音，田春华

(1.北京邮电大学 经济管理学院 北京 100876; 2.上海对外经贸大学工商管理学院 上海 201620; 3.清华大学 软件学院 北京 100084)



【统计调查与分析】

电影首映日后票房预测模型研究

罗晓芃1，齐佳音2，田春华3

(1.北京邮电大学 经济管理学院 北京 100876; 2.上海对外经贸大学工商管理学院 上海 201620; 3.清华大学 软件学院 北京 100084)

利用285部电影的截面数据进行单样本t检验，发现票房过亿电影的首映日票房都不少于200万元。抽取138部首映日票房超过200万元的电影的21天数据构建动态面板模型，采用两步系统GMM估计建立票房预测模型。研究表明：前一日票房对后一日票房具有显著正向影响，即在一段时间内前一日票房增加将提升后一日票房。票价较高和较低都会对票房产生积极影响，因此将票价纳入票房预测模型中。电影类型、上映日期、上映档期、出品国别、续集、网络评分、点映活动均被证明对票房具有正向影响。相较其他研究，包含上述指标的预测模型准确率得到了大幅提高。

首映日；票房预测；动态面板；广义矩估计方法

一、引 言

作为电影短暂产品生命周期中最主要的回报，票房不仅直接反映了一部电影给投资公司所创造的经济价值，而且从侧面反映了电影的艺术质量和商业策略，是衡量电影成功与否的重要指标，自然而然地体现出电影作品的市场需求度和投资吸引力。此外，电影是天然的体验型商品，消费者只有消费并体验之后才能了解电影的价值，所以消费者会寻求更多关于电影价值的信息进行消费决策，而代表大多数人消费决策的电影票房也自然而然成为判断电影价值的质量信号之一[1]。因此，电影票房不仅影响到电影产业从业者的经营决策，同时也影响到电影观众的消费决策，如果能够提前预知电影产品在市场中的接受程度和盈利能力，将对电影产业链各环节的决策产生巨大影响。因此，对电影票房进行准确预测，无疑对风险控制和决策具有重要的现实意义。

然而由于电影票房的特殊作用，在市场的多方博弈下，影响电影票房的因素无疑是复杂的。以往研究表明，电影类型、主创号召、获奖提名、上映档期、营销手段等都会影响到电影票房成绩[2-3]，且近年来随着互联网的发展，在线评论、网络评分等因素也被纳入票房预测的考察范围[4]。然而，大多数研究忽视了对票房、排片、上座率等市场信息的理解和运用。上述市场信息每日均在发生变动，相比于其他的电影信息能够更为直接、快速、敏锐、动态地响应电影市场的需求变化。尽管目前已有研究发现了动态市场信息的价值，并利用周票房进行总票房的预测研究[4-6]，但是未能充分挖掘电影市场信息的动态性和直观性，尤其缺乏基于日票房进行短期滚动票房预测的相关研究。本文尝试以质量信号传递理论为基本理论框架，构建基于首映日后的电影前一日票房、票价等动态市场信息对后一日票房短期滚动预测的票房预测模型。通过两步系统GMM估计动态面板数据发现，基于前一日票房的预测模型的平均绝对百分比误差仅为8.54%，相较其他的研究，本研究中的模型预测准确率获得大幅提高。

二、文献综述

(一)基于静态电影信息的票房预测研究

早期的票房预测研究中，学者们重点关注的是主创影响力、电影类型、MPAA评级、发行档期、是否为续集、影评人评论、获奖及提名、制作预算、广告成本等与电影票房的因果关系[7]。上述因素基本在电影上映前就已被固定并不再改变，因此，可以认为是静态的电影信息。从这一角度来看，电影票房可以看作是各静态因素综合作用效果的财务呈现，只要总结和建立一套票房成功电影的标准，并基于该标准对票房进行比对，就能获得准确的票房预测结果。

由于样本数量、预测技术、计量误差等限制，每个因素对票房影响的研究结论都不尽相同，但总结大量文献发现，电影类型、上映档期、电影续集等电影产品特征信息对票房的影响被一致认为是显著的。因此，应当将证实有影响的静态电影信息纳入票房预测模型中。

(二)基于动态电影信息的票房预测研究

伴随信息时代的来临，在线评论、网络评分、网络搜索逐渐成为了影响票房的巨大力量，这些信息能够在电影上映后不断变动，并能对应上映周期中的不同时间段对电影产生全方位的作用，因此可以认为是动态的电影质量评价信息。研究表明，在线评论数与电影票房收入密切相关，且上映初期的在线评论数可以较为准确地预测上映初期的票房[5，7]。网络评分作为在线评论的综合体现，被证实在广告的推波助澜下可以帮助高评分的电影大幅提高票房收入[4]，整合了网络搜索的票房预测模型也能够显著提高首映周和后续周票房的预测精度[6]。此外，票房、排片、上座率、票价等反映电影市场表现的信息同样能够在电影上映后不断变动并在上映周期中的不同时间段产生不同作用，因此可以认为是动态的电影市场信息。研究发现，科学的排片决策对票房成绩具有显著提升作用[2，8]。李波、董纪昌和汪寿阳对电影票价的调研则显示，电影票价偏高仍是制约国内电影市场发展的重要因素，但票价的制定也并不是越低越好[9]。

不论是数量变动还是内容的变动，动态电影信息都可能由于网络空间的放大效应对票房形成冲击，且这一效应在电影短暂的生命周期中更为显著，因此，票房预测应该更多地考察动态信息的作用。

(三)质量信号理论与票房预测研究

作为体验性商品的电影产品，相较于其他普通商品具有如下特点：一次性消费，即电影消费者在观看过一次电影后，一般不会再购买第二次。信息不对称，即电影消费者只有在消费并体验之后才能知晓电影的价值。因此，观众选择电影产品时始终处于信息不对称的情境中，只能通过搜寻和电影有关的信息作为质量信号推测和评估电影真实质量[10]。与此同时，质量信号的数量和质量信号的可靠性都会影响观众对电影质量的评估，电影的质量信号越多、可靠性越高，观众越能准确估计电影的质量，产生的疑虑和可能承担的风险也越低，从而提高电影被选中的几率[11]。从质量信号理论角度出发的票房预测研究大多考察了续集这一质量信号的作用。Basuroy、Desai和Talukdar等学者认为续集电影基于已有的品牌，为观众提供了更多与电影故事背景、人物角色有关的质量信号，而广告则加速了这一质量信号传递过程，证实了电影产品中的质量信号传递现象，并发现续集和广告费用对票房收入产生了积极作用[10]。

从质量信号理论角度建立的票房预测模型以清晰的目的性从错综复杂的影响因素中甄选预测票房的指标，不仅使模型变量的选择更为准确，同时也简化了模型设计的步骤，提高了模型建立和应用的效率。

三、票房预测模型理论建模

如前所述，根据质量信号理论，在信息不对称的情景下，缺少信息的一方会通过质量信号推测真实信息。由于观众在电影上映前并不知道电影的真实质量，因此只能通过表征电影价值的质量信号推测电影的质量。基于此，本文试图探索准确且有效传递电影价值的质量信号因素，构建基于首映日后票房的预测模型。

(一)解释变量的选择

前一日票房。在消费市场中，消费者的每次购买都是独立的决策过程[12]，产品的销量意味着选择产品的人数，也意味着其他消费者对该产品质量的认可，因此产品的销量是重要的质量信号。就电影产品而言，消费者同样会假设多数人是正确的，并参考他人的决策结果做选择，因此反映多数人决策结果的电影票房即为电影价值的质量信号。此外，诸多研究表明，电影票房在时间维度上存在显著的自相关性和滞后效应，不仅上周票房的增加极有可能促使下周票房的增长[2]，前一日票房的增加也极有可能促使后一日票房的增长，这意味着前一期的票房成为了电影质量信号，不断影响着后一期的票房。

排片。电影在影院的排片在一定程度上影响了电影的票房，一方面是由于排片量越高，电影占用的屏幕数、放映时间等资源越多，观众对其他影片的选择性也就越低，因此更有可能获得票房的成功；另一方面，排片也反映了影院对电影的市场预期，一定程度上也成为了传递电影价值的质量信号。

观影人数。观众对电影需求的一个直观表现就是观看电影人数的多少，具体又表现为观影人数和上座率。从观众需求角度出发的电影票房研究表明，观众的观影行为与票房密切相关，甚至可通过研究观众的需求变化进行票房的预测[13]。然而，上座率不仅与观众需求有关，也与影院排片密切相关，不合理的超量排片可能反而导致上座率下降。因此，本文采用直接反映观众需求的观影人数作为模型的解释变量。

票价。尽管电影票价在短期内不会有大幅波动[14]，但片方往往会根据对电影的市场预期设置不同档次的票价，电商、会员等售票渠道也会根据电影的市场预期采用不同的票价补贴，此外，低廉的观影票价也可能在一定程度上吸引更多观众，因此，本文采用电影票价作为模型的解释变量。

(二)控制变量的选择

控制变量的选择参考了现有电影票房预测研究。然而，由于本文希望依据上映后数据进行预测，因此排除了在电影上映前属性未知的变量。基于上述考虑，最终选择的控制变量包括：电影类型、上映日星期数、是否在档期内、出品国别、是否是续集、网络评分和是否有点映。

电影类型。电影票房的影响因素众多，而电影类型与个人观影偏好紧密相关，往往成为影响观众观影意愿的重要因素。参照以往研究，将电影类型分为七类，即爱情、动作、剧情、喜剧、动画、惊悚以及科幻。

上映日期。国内电影市场上普遍存在周二特惠、周四首映等情况，因此上映当日在一周中的星期数往往可能影响消费者的观影选择。

档期。诸多研究发现，暑期档等特别的上映档期对电影票房的影响显著。本文中的档期定义为如下三个时段：贺岁档，指从11月20日左右开始直到春节长假结束，以影片大规模上映为开端；暑期档，指每年6月1日至8月31日的时段内，主要受众为4～24岁的学生观众；国庆档，指每年国庆节7天长假期间。

出品国别。由于院线每年合法引进的电影数量仅有60部左右，出于商业目的，院线往往选择引进大制作商业片，而观众往往因为精良质量和演员阵容选择观看进口大片，因而进口电影与国产电影表现出明显的票房差别。

续集。续集电影借助原有品牌(包括原电影、歌曲、漫画、电视节目甚至游戏)的形象和影响，在人物形象、故事情节、场景设置等环节上都有了基础，较为容易获得市场认可，同时也是明显的质量传递信号。

评分。发达的网络促使观影口碑成为影响票房的因素之一，但对于网络评论而言，非结构化数据的处理和中文文本分析相对困难，而网络评分可以认为是主流口碑的反映，能够代表大部分评论的情感倾向。

点映。点映是电影正式上映前的小规模放映，旨在酝酿观影口碑，并提前锁定一部分票房，已经成为很多电影的发行营销策略之一。在口碑效应日益放大的今天，点映的作用也不容忽视。

(三)理论模型

前一日票房影响电影票房的机理主要体现为质量信号的传递作用和电影市场中供需要素间的动态相关性。首先，某电影前一日分配的银幕数量对当日票房产生影响，而前一日票房是重要的质量信号，反映了观众对影片的质量认可和观影选择。其次，当日实际实现的观影需求情况更新了院线对其后一日票房表现的期望，反映了观众的需求(表现为观影人次、)与市场的供给(表现为放映场次)是否达到最优，从而对后一日的银幕分配(表现为计划排片)决定产生影响，而该决定和后一日的票价又再次影响了后一日的票房，如此类推。

此外，影片类型、上映日期、档期、出品国别、续集、评分、点映等作为外生变量被设置为控制变量。票房预测模型的建立理论框架如图1所示。

图1 模型理论框架

在模型形式方面，对数线性模型中自变量的系数估计能直接反映其对因变量的弹性，并且对数形式不仅与多阶段消费者决策过程的相关理论模型相符合，还可以平滑模型中变量的分布，使变量间关系趋于线性化。因此，模型将采用对数线性模型形式。为清晰地考察控制变量与票房的关系，控制变量以乘法形式进入模型。

综上所述，结合文献研究及变量设定，构建理论模型如式(1)所示，其中ui和εit分别为电影i的固定效应和扰动项。

lnbox-officeit=β0+β1lnbox-officeit-1+β2lnscreenit+β3lnaudienceit+β4lnpriceit+β5lnprice2it+β6lnbox-officeit*genre+β7lnbox-officeit*weekday+β8lnbox-officeit*season+β9lnbox-officeit*country+β10lnbox-officeit*sequal+β11lnbox-officeit*score+β12lnbox-officeit*dianying+ui+εit

(1)

模型中各变量含义见表1。

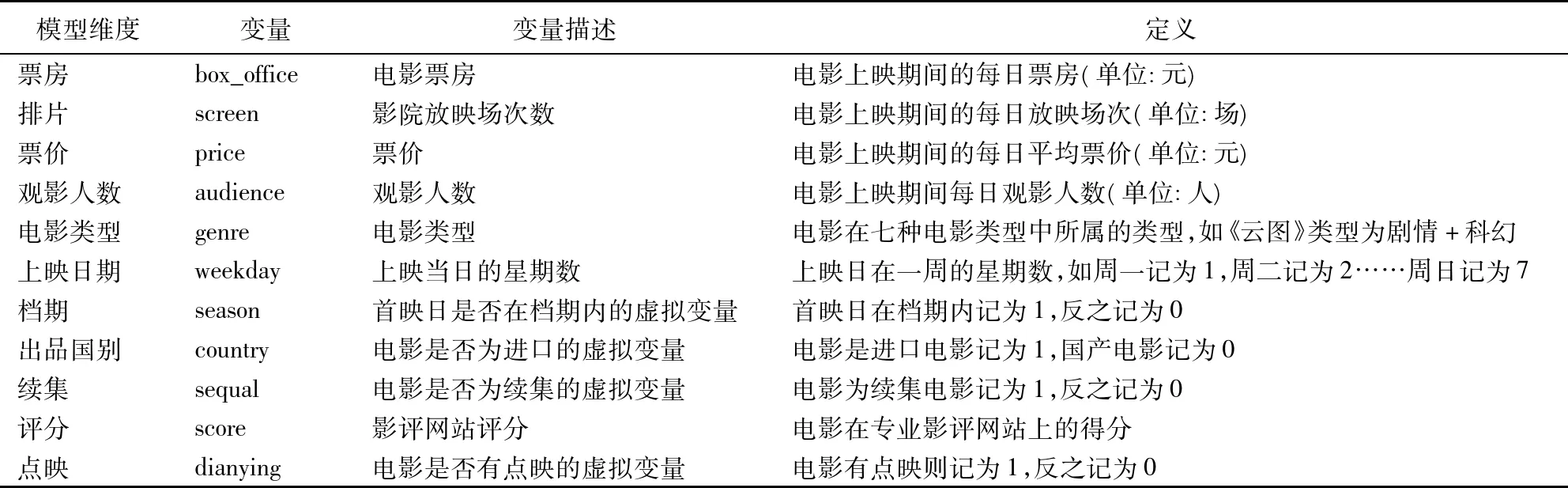
表1 模型变量表

四、实证研究

(一)数据与变量

本文以2012年5月至2015年8月在中国内地上映的285部影片作为研究对象，分别收集每部影片的日票房、排片数、观影人数、上映日期、是否在档期内、平均票价、电影类型、国别、是否为续集或翻拍电影等信息。票房、上座率、排片等经营数据来源于电影票房数据库网站(http://58921.com/)，评分、类型、国别等特征数据来源于豆瓣电影网站(https://movie.douban.com/)，其中为面向行业应用并保证准确性，经营数据选取当前全国市场份额第一的某院线数据。

从市场效益的角度看，考察有潜力获得票房成功的电影相比考察全部电影而言更为符合市场需求。从模型预测的角度看，以往考虑所有票房层次电影的票房预测模型的准确度都不高[6]。从业界实践的角度看，首映日票房高于200万元人民币的电影获得票房成功的可能性更大*笔者曾与产业界从事过票房预测研究的专家进行深入讨论并获悉这一经验结论。。因此，对影片进行分类研究是提高票房预测模型准确性的可行办法。本文以首映日票房的高低为分类依据对样本中的影片进行划分，将所有285部影片按照首映日票房大于等于200万人民币和小于200万人民币分为“高票房组”和“低票房组”。

经统计，“低票房组”共有137部影片，总票房均值为5 255 629.92元；“高票房组”共有148部影片，总票房均值为108 469 507.4元。设定总票房超过1亿元人民币为票房成功(不考虑影片成本情况和实际盈利)，分别对两组影片进行单样本t检验。如表2所示，低票房组的双侧Sig值为0.000<0.01，因此，我们认为在0.01的显著性水平下，低票房组影片的总票房与1亿元有显著性差异；而高票房组的双侧Sig值为0.839>0.01，因此，认为在0.01的显著性水平下，高票房组影片的总票房与1亿元没有显著性差异，表明当电影的映日票房大于等于200万元时，则其平均总票房将接近甚至高于1亿元。

表2 高低票房组t检验结果表

因此，为准确有效地进行电影票房预测，本文选择以首映日票房大于等于200万元的电影作为研究对象。经过数据收集整理，排除数据缺失等问题，共获得138部电影的面板数据作为票房预测样本，进行后续总票房预测研究。

(二)描述性统计

对票房预测样本的138部电影进行描述性统计分析，部分变量的描述性统计如表3所示。其中，总票房最大值超过7亿元人民币，最小值也超过了1.1亿元；平均上座率为22.79%，平均上映时间为32.65天，平均票价为72.02元；网络评分最低至3.4分，最高达9.1分，平均评分为6.556；总票房、首映日票房、放映总场次、观影总人数几个变量的标准差非常大，表明即使同样属于“高票房”组，不同电影之间的票房、排片和观影人数等仍存在较大差异。

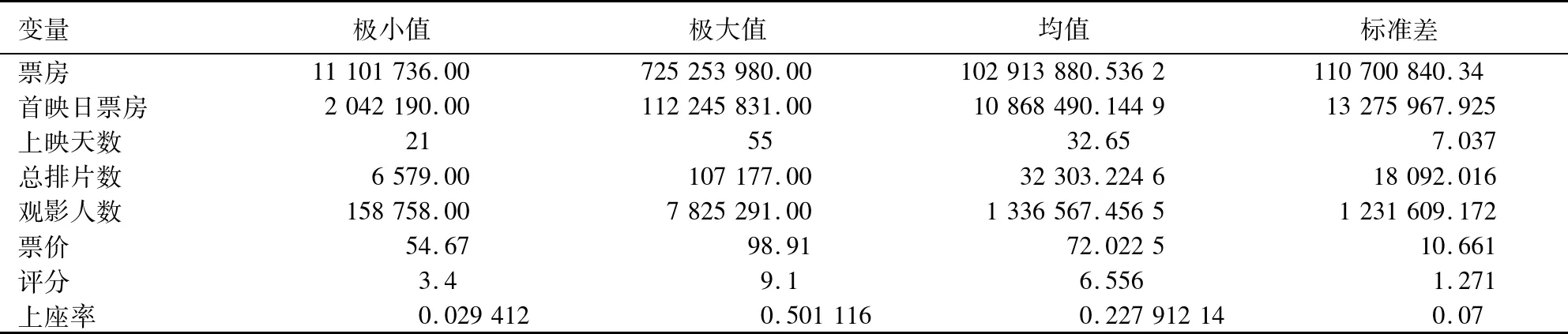
表3 变量描述统计表

此外，138部电影中，选择在周五首映的电影为55部，其次选择在周四首映的电影为40部，59.4%的电影选择在档期内上映；国外引进电影为54部，国产电影为84部；续作电影共44部，占比31.9%；电影类型中含有动作、剧情、喜剧元素的电影最多，占比超过30%；39.9%的电影选择小规模点映，以便制造口碑效应，提前锁定票房。

(三)变量说明及处理

1.自变量。如前所述，总票房、首映日票房、放映总场次、观影总人数的标准差非常大，呈现出极强的偏态性，因此以总票房为被解释变量的回归中随机干扰项通常具有异方差性。为了减弱异方差的不良影响，以往的研究中多将总票房的对数作为被解释变量[9]。本文中同样以票房对数化的形式进入模型，在数据预处理阶段，采用离差标准化方法对数据进行标准化，使各变量观察值的数值范围都在[0,1]之间。此外，由于对数形式须确保所有变量值为正值，因此将每个标准化后的数据都加上0.000 001。随后，作对数化票房变量与其他变量水平项和对数化形式的散点图，发现对数化票房与其滞后一阶、对数化放映场次、对数化观影人数呈现出明显的线性相关性。此外，根据电影票价的理论含义和散点图，发现对数化总票房与场均票价平方项以及票价水平项具有一定的线性相关性，因此，以对数化票价平方项和水平项进入模型。

2.控制变量。电影类型方面，由于同一部电影的类型可能同时包括两到三类，因此，分别以2012-2015年四个年度中国内地票房排名前25的电影的各类型占比为当年度题材得分*电影类型与票房排名的信息来源于中国票房网(http:∥www.cbooo.cn)。，并为样本中的电影赋予当年度的题材得分。表4为2012-2015年度的电影类型题材得分表，可以发现动作和剧情类别的电影在三年中的题材得分均超过20%，喜剧、科幻、爱情、惊悚类型电影的题材得分依次下降。由类型得分的定义可知，一部电影的类型得分越高，表明该部电影涉及的类别更可能涉及题材得分高的类型。

表4 电影类型题材得分表

上映日期方面，将138部电影上映三周的每日票房按照周一至周日的星期进行分类加总，计算每日票房占所有电影总票房的比例，将比例作为上映日的星期得分。星期得分计算表见表5。其他变量方面不做处理。

(四)相关性分析

为尽量避免多重共线性问题，首先对对数化票房一阶滞后项、对数化放映场次、对数化观影人次、对数化票价及其平方等自变量，以及出品国别、是否为续集、电影类型、网络评分、是否在档期内、是否提前点映等控制变量进行相关性分析。

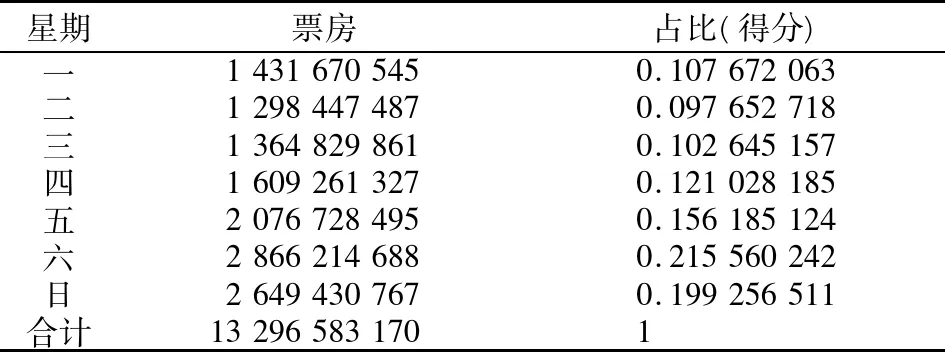
表5 星期得分表

表6 解释变量相关系数表

表7 控制变量相关系数表

由相关分析可以看出，对数化放映场次和对数化观影人数与对数化票房的滞后一阶相关系数超过0.90，故将上述两变量予以剔除。控制变量之间的相关系数的绝对值均未超过0.7，表明无严重线性相关，可以进入回归模型。

(五)模型估计与结果分析

根据前述研究设计，被解释变量的动态滞后项是模型的解释变量之一，因而该滞后被解释变量与随机误差组成部分中的个体效应相关，造成了估计的内生性，若采用其他估计方法如OLS估计等则可能导致“动态面板偏误”。为获得无偏的估计值，且考虑面板数据样本为“大N小T”形式，因此利用广义矩估计方法(Generalized Method of Moment，简称GMM)。GMM估计包括差分GMM估计和系统GMM估计，其中后者是前者的扩展，避免了前者的弱工具变量问题，且减少数据变换步骤，从而提高了估计的效率[15-16]，因此，本文选择系统GMM估计方法。进一步地，对模型进行两阶段估计，即第一阶段进行稳健性估计获得系数显著性的统计推断，第二阶段利用之前估计得到的残差构造方差-协方差矩阵重新估计，获得表征模型筛选结果的Sargan统计量。系统GMM两阶段法消除了第一阶段的异方差问题和第二阶段的向下偏误，从而得到了一致且有效的估计量。

在使用GMM方法估计动态面板数据模型时，采用平衡面板(即每个观测值的时间序列长度相等)的估计更为准确有效。由于电影上映时间不一，但大部分都能上映三周以上时间，因此以138部电影上映3周(21天)的每日数据构建动态面板数据样本进行模型估计。在估计过程中，为避免模型的估计受到各解释变量间可能存在的多重共线性影响，本文在建模中先单独输入各解释变量，在其单独效应显著的基础上，再采用逐步回归方法引入影响显著的解释变量，以确定最终模型。模型估计结果如表8所示。

表8 模型估计结果表

对模型的检验结果显示，AR(2)检验p值为0.112 0>0.1，Sargan检验p值为0.999 8>0.1，在0.1的显著性水平上通过检验，因此模型拟合效果良好。

估计结果中，主要的解释变量前一日票房(lnbox-officeit-1)的系数值为0.011 4，表明在其他条件不变的情况下，电影的前一日票房增加一倍，后一日票房将提高1.14%。系数为正值，证明了票房作为质量信号在传递电影价值信息时具有确定的正向积极作用，能够帮助提拉电影后续票房。显著的滞后一阶变量系数表明，前一日票房在票房预测中能够有效替代排片、观影人数变量的解释作用，对后一日票房形成直观、动态、综合的市场预期指标。另一解释变量票价的水平项(lnpriceit)系数为正，而其二次项(lnprice2it)系数为负，表明票价在低位和高位时的变动更容易引起票房的变化，即票房对低位票价和高位票价的变化更为敏感，可能的原因是低票价降低了观影门槛，刺激了观影热情，促使部分原本不属于目标消费群体的人群成为观影人群，从而快速、大量地积累票房。而高票价的电影在各类质量信号的保证下也能够捕获一定的销量，在高票价带来的高溢价下保证了电影票房的持续增长。

其他控制变量中，系数均为正且显著，表明电影类型、上映日期、上映档期、出品国别、续集、网络评分、点映活动均被证明对票房具有正向影响作用。总结上述影响因素，可以说明一部票房成功过亿的电影所具备的基本产品特征为：电影类型(genre)涉及动作、剧情、喜剧等元素，首映日在档期(season)内，是进口(country)的续集电影(sequal)且有点映活动(dianying)，还应当具有较好的质量，即网络评分(score)越高，票房表现越好。只要一部电影具有上述特征中的任意一项特征，都将在一定程度上提升票房。此外，电影上映当日在一周中的星期数(weekday)被证明对当日票房有一定的影响作用，即星期数越大，票房越高。因此，电影发行方在选择首映日时应当考虑尽可能地增加在大星期数日上映的机会，从而更多地捕获接近周末和周末的票房。

(六)模型检验

1.参数一致性检验。对面板数据模型而言，如不存在滞后项，则可选择混合回归估计。如仅存在被解释变量滞后项，则可进行固定效应回归。而对于既存在滞后项又存在固定效应的动态面板模型，上述两种估计都是有偏误的，但这两个估计的系数应该是真实系数的上限和下限，因此正确估计的GMM估计值应该介于混合回归和固定效应估计的系数之间。由表9可知，排除了滞后项的其他各变量系数中，混合回归估计量最大，固定效应估计量最小，系统GMM估计量介于两者之间，表明预测模型估计结果可靠。

表9 参数一致性检验表

2.预测效力检验。本文利用样本外预测分析方法对模型进行了预测效力检验。通过使用0.632自助法进行抽样，将样本分为训练集(约三分之二)和测试集(约三分之一)，其中测试集中共有46部样本电影，920对每日票房观测值和预测值。比对观测值和预测值的结果，可以发现票房的预测值与观测值基本重合，且数值波动趋于一致，显示出良好的预测效果。检验结果表明，本文中票房预测模型的平均绝对百分比误差MAPE为8.54%，比较相似的研究，Liu的首映周票房预测误差为38.0%，王炼、贾建民的周票房预测误差为28.0%，因此，基于前一日信息并以单日票房为预测目标的票房预测模型具有更高的准确性。

五、研究结论与讨论

本文尝试以质量信号传递为基本理论框架，结合经典研究中的票房影响因素，探究基于首映日后票房的预测模型。实证研究表明，首映日票房大于等于200万元与总票房过亿存在统计意义上的关联，因此以首映日票房是否大于200万元为标准对电影进行分类探讨符合实践和理论研究的要求。此外，从质量信号传递角度出发遴选的动态电影市场信息对电影票房具有很好的指示作用，以日为单位的滚动预测大幅提高了票房预测模型的准确率。

研究结果表明，票房是传递电影价值信息的重要信号。合适的上映时机、恰当的推广宣传以及影片本身良好的质量能够帮助电影捕获较高的首映日票房，形成积极的市场信号。具体而言，电影选择在合适的档期内上映，符合电影的需求波动特征及人们的观影消费习惯，从而更多地吸纳票房。选择在接近周末的时机首映，能够更多地捕获休息日激增的票房。合理安排小规模的点映活动帮助电影提前锁定部分票房，并酝酿口碑效应，在市场上形成更多的质量信号。具备动作、剧情、喜剧等广受欢迎的类型元素，且拥有续集熟悉框架的故事保证和进口精良制作的质量保证的电影，能够以较少的信号形成相对准确的观影预期，同样也帮助电影尽可能增加票房。

在上述决策的作用下，电影在上映伊始即收获较高的首映日票房，随即形成传递电影价值信息的重要信号，在电影上映初期直观地向市场释放利好信息，建立市场信心，初步形成对整个电影上映周期中票房成绩的市场预期。首映日后电影的前一日票房不断为后一日票房的市场预期补充信息，刺激短期的排片供给与观影需求相互转化，从而进一步提拉票房。在首映日票房传递的指向性信号和每日票房传递的补充性信号的共同作用下，具有较高首映日票房的电影更容易获得票房成功，以拥有较高首映日票房电影为研究对象的票房预测模型也取得了良好的预测准确性。

本文对票房预测研究领域有如下贡献：第一，本文从质量信号传递角度甄选预测模型指示变量，发现和证实了动态市场信息对票房预测的影响作用。第二，不同于以往研究，本文缩短了票房预测的时间周期单位，基于前一日信息对后一日票房进行滚动预测，将前一日票房对电影市场的供给(排片)和需求(上座率)进行关联，强调了电影市场中各要素的动态关系。第三，预测效力检验表明，相比于其他类似研究，基于前一日票房数据的票房预测模型能够提高票房预测的准确性。对行业应用层面而言，利用前一日票房进行票房预测提供了电影票房的合理预期，相比以往需综合考察排片、上座率、观影人次等多指标进行电影产品供给决策，利用票房信息进行票房预测的直观指标参考体系有效降低了决策复杂度，为电影投资方和发行院线在制定排片策略、选择上映时机、制造口碑效应等方面提供了科学客观的参考依据。

本文的研究局限及未来展望如下：由于数据可获得性的限制，尽管在动态电影信息方面有网络评分反映网络评论情感倾向，但难以全面囊括网络传播对电影票房造成的影响，因此得出的结论具有一定的局限性。因此，基于反映网络传播影响因素如网络评论、话题热度等的单日票房预测研究将成为今后的研究方向。

[1] ByengHee Chang, EyunJung Ki. Devising a Practical Model for Predicting Theatrical Movie Success: Focusing on the Experience Good Property[J]. Journal of Media Economics, 2005(4).

[2] Elberse A， Eliashberg J. Demand and Supply Dynamics for Sequentially Released Products in International Markets: The Case of Motion Pictures[J]. Marketing Science, 2003(3).

[3] Basuroy S, Chatterjee S,Ravid S A. How Critical are Critical Reviews? The Box Office Effects of Film Critics, Star Power, and Budgets[J]. Journal of Marketing, 2003(4).

[4] Moon S. Dynamic Effects Among Movie Ratings, Movie Revenues, and ViewerSatisfaction[J]. Journal of Marketing, 2010(1).

[5] Duan W, Gu B, Whinston A B. Do Online Reviews Matter? An Empirical Investigation of Panel Data[J]. Decision Support Systems, 2008(4).

[6] 王炼, 贾建民. 基于网络搜索的票房预测模型——来自中国电影市场的证据[J]. 系统工程理论与实践, 2014(12).

[7] Liu Y. Word of Mouth for Movies: Its Dynamics and Impact on Box Office Revenue[J]. Journal of Marketing, 2006(3).

[8] Swami，Eliashberg，Weinberg. Silver Screener A Modeling Approach to Movie Screens Management[J].Special Issue on Managerial Decision Making, 1999(3).

[9] 李波, 董纪昌, 汪寿阳. 中国电影票价与受众关系的实证研究[J]. 管理评论, 2009(4).

[10]Basuroy S, Desai K K, Talukdar D. An Empirical Investigation of Signaling in the Motion Picture Industry[J]. Journal of Marketing Research, 2006(2).

[11]Kirmani A． Advertising Repetition as a Signal of Quality: If It’s Advertised so Much，Something Must be Wrong[J]. Journal of Advertising, 1997(3).

[12]Hennig-Thurau T, Houston M B, Heitjans T.Conceptualizing and Measuring the Monetary Value of Brand Extensions: The Case of Motion Pictures[J].Journal of Marketing, 2009(11).

[13]Ainslie A,Ze X, Zufryden F. Modeling Movie Life Cycles and Market Share[J]. Marketing Science, 2005(3).

[14]Chance D M,Hillebrand E, Hilliard J E. Pricing an Option on Revenue from an Innovation: An Application to Movie Box Office Revenue[J]. Management Science, 2008(5).

[15]Roodman D. How to Do Xtabond2: An Introduction to "Difference" and "System" GMM in Stata[J]. Stata Journal, 2009(1).

[16]段元萍，王鑫鑫.中国电影贸易出口影响因素的实证分析[J].西安财经学院学报，2015(3).

(责任编辑：李 勤)

Box Office Forecasting after Premiere

LUO Xiao-peng1，QI Jia-yin2，TIAN Chun-hua3

(1.School of Economic and Management, Beijing University of Posts and Telecommunications,Beijing 100876;2.Management School, Shanghai University of International Business and Economics,Shanghai 201620;3.School of Software, Tsinghua University, Beijing 100084)

Based on the cross- sectional data of 285 films, we found that the movie whose premiere box office exceeds two million Yuan could often attains over one hundred million Yuan in total box office. Then we extracted 138 films whose premiere box office was over two million Yuan, and created a dynamic panel data sample with 21 release days' data, established a box office forecasting model by two-step system GMM estimation method. As a result, the previous day's box office has a significant and positive impact on the next day's box office, and ticket price will affect total box office when the price is relatively high and low. Genre, releasing weekday and season, produced country, sequel, rating score, and early small-scale releasing are proved to influence box office. Combined with these factors above, the box office forecasting model has achieved much higher accuracy than other research.

premiere; box office forecasting; dynamic panel; GMM

2016-05-06

国家自然科学基金重点项目《面向不确定性的Web2.0用户创作内容管理研究》(71231002)；国家自然科学基金重大研究计划培育项目《大数据驱动的三类典型工商市场主体风险识别决策研究》(91546121)

罗晓芃，女，云南昆明人，博士生，研究方向：大数据风险识别； 齐佳音，女，陕西洛南人，教授，管理学博士，研究方向：社会化客户关系管理，大数据驱动的管理决策； 田春华，男，山东济宁人，工学博士，研究方向：工业大数据分析。

J943∶O211.67

A

1007-3116(2016)11-0094-09