基于MapReduce的相似自连接新方法：过滤和内切圆算法

鲍广慧 张兆功 李建中,2 玄 萍

1(黑龙江大学计算机科学与技术学院 哈尔滨 150080)2(哈尔滨工业大学计算机科学与技术学院 哈尔滨 150001)(851890784@qq.com)



基于MapReduce的相似自连接新方法：过滤和内切圆算法

鲍广慧1张兆功1李建中1,2玄 萍1

1(黑龙江大学计算机科学与技术学院 哈尔滨 150080)2(哈尔滨工业大学计算机科学与技术学院 哈尔滨 150001)(851890784@qq.com)

相似自连接是一个在很多应用领域中很重要的问题.对于海量数据集，MapReduce可以提供一个有效的分布式计算框架，相似自连接操作也同样可以应用在MapReduce框架下.但已有研究工作仍然存在不足，如对于聚集数据区域采用加细划分方法，目的是负载平衡，但不易实现.现有的算法不能有效地完成海量数据集的相似自连接操作.为此提出了2个新颖的基于MapReduce的相似自连接算法，其思想是采用坐标过滤技术，形成有效候选集，以及针对聚集区域采用六边形划分的内切圆算法.过虑技术是在等宽网格划分基础上，利用同一维坐标间的距离差与相似性约束阈值ε进行比较，可以明显地减少候选集的数量，也证明了六边形划分是所有正多边形全覆盖中最优的划分方法.实验结果表明：新方法比其他算法有更高的效率，提高效率80%以上，它能够有效地解决有聚集区域的海量数据集的相似自连接问题.

海量数据集；过滤；相似自连接；数据划分；Hadoop平台；MapReduce编程模型

连接操作(join)是一个很重要的数据库操作，相似自连接是join的一种特殊类型，即对同一数据类型进行相似自连接操作.它在数据分析中扮演很重要的角色：数据清理[1]、相近的文本查重[2]、文件相似性分析[3]和数据挖掘等工作，特别在基于密度的聚类分析中也用到了相似自连接操作的结果.大规模的相似自连接的有效实现可以加速这些数据的分析过程.本文中，我们主要研究基于MapReduce的海量数据集的相似自连接操作.

关于集合R，S的θ-join的定义为

R▷◁θS=σθ(r,s)={(r,s)|d(r.A,s.A)≤ε}，

(1)

返回结果为所有的相似对(r,s)，它们的距离在属性A上不会超过一个最大阈值ε.ε叫作相似自连接的约束，一般由用户给定.文中的距离采用欧几里得距离.

对于海量数据的并行分析与处理，各种各样的编程模型相继被开发出来. 从基本的数据库操作到高水平的数据挖掘方法，像聚类、分类和离群点检测[4].由Google提出的MapReduce编程模型以及它在Hadoop上的开源实现受到了广泛的关注和使用.

在MapReduce框架下针对相似自连接的问题已有3种方法被提出来.在文献[4]中，MRDSJ算法被提出，主要利用等宽网格的方法来减少不必要的距离计算,可以有效地进行数据集的相似自连接操作.但是这个方法不能够处理聚集的数据，需要对等宽的网格划分实行进一步加细划分，目的是实现每一个计算节点的负载平衡.同时对于大规模的数据集合，会产生多余的候选集，严重的影响了算法的效率.为此提出了2个新的算法——过滤算法和内切圆算法.过虑算法是在等宽网格划分基础上，利用同一维坐标间的距离差与约束ε进行比较，可以进一步减少候选集的数量.内切圆算法是针对数据聚集区域利用距离的三角不等式，可以快速准确地计算出结果集，避免了每一对点之间的join运算.通过实验结果分析可以看出我们的算法可以减少不必要的计算，不需要加细划分，并且效率有80%的提高.

本文的主要贡献有3点:

1) 我们提出了一个新的过滤算法，它在Map-Reduce的框架下来处理海量数据集的相似自连接操作，利用过滤技术有效地减少了候选集的数量.提出了新的降低维数方法，维度从n维降到2维.

2) 我们提出了一个新颖的内切圆算法，它特别适用于聚集的数据集.我们还提出了新奇的正六边形区域划分方法，它使得相邻点的距离信息被充分的利用，进一步提高了内切圆算法的效率.我们还证明了正六边形区域划分方法是最优的.

3) 应用我们的新算法在真实的生物数据集上，实验结果显示随着数据量增加，算法执行时间呈现近于线性的增长.

1 相关工作

相似性连接是一种很重要的操作，目前被大量学者研究，其中庞俊等人[5]对相似性连接查询技术做了综合论述，提出了相似性连接的具体分类.针对数据类型的不同，可分为向量相似性连接、集合相似性连接、字符串相似性连接;按照返回结果分为所有对相似性连接、基于阈值的相似性连接、Top-k相似性连接和KNN相似性连接等.

大规模的海量数据的连接操作是一个计算代价很高的操作，随着数据规模的逐渐增大，如何在分布式的环境下利用MapReduce并行的执行相似性连接操作也引起了研究者们的关注.在文献[6]中，马友忠、孟小峰等人研究了在MapReduce框架下海量高维向量的并行Top-k连接查询，主要结合符号累计近似法和基于阈值估计法，提出了基于SAX的Top-k的连接查询算法，返回符合条件的前k个向量对;文献[7-8]主要研究在欧几里得空间上的KNN连接，文献[8]的作者提出了利用空间填充曲线转换KNN连接在一系列一维范围内搜索的想法，使问题转化在基于泰森多边形法分区允许一个有效地连接操作;文献[8-9]中提出数据分区方法，需要一个或多个join操作运行在数据集合上的连接算法;文献[10]概述了MapReduce下常见的连接策略;然而，绝大多数的现有工作关于并行的连接都采用的是等值连接；Afrati等人[11]提出了优化策略对于多维度的等值连接.但是他们并不能应用于相似性连接.广播的连接策略依赖于不同属性的数据集之间的操作.它也并不适用于自连接这种相同数据集的连接操作;文献[12]里提到一种有效地相似连接算法用于解决编辑距离约束，它把编辑距离约束转换为2个字符串间的匹配q-grams的数量上;文献[13]对KNN相似性连接已有方法进行了对比分析;文献[14]对多元连接进行优化，以降低IO代价为目标并针对MapReduce设计一个并行执行策略提高多元连接的性能.

文献[3]提出利用MapReduce的自连接操作处理稀疏的文件集，采用有效地剪枝策略通过分区策略可以克服内存的瓶颈，并且提高了效率；针对大规模的矢量数据的分析，文献[4]中作者提出在Map-Reduce框架下基于距离的相似自连接.利用数据分区，等宽网格划分的方法来减少通信和不必要的距离计算的数量，它比较适用于低维度到中维度；他们又继续改进算法，针对于高维度的矢量数据他们又提出了PHIDJ算法，可以适用于在MapReduce下的并行相似自连接操作[15]；PHIDJ算法主要是利用加细网格划分来处理聚集的数据，但不易实现.并且这种方法仍然存在不必要的计算，针对聚集区域的数据仍没有有效的方法进行处理.效率还有待提高，这正是我们要突破的地方，需要进一步研究.

1.1 MapReduce框架下的MR-DSJ算法

作为背景介绍，在文献[4]中，作者提出一个基于等宽网格划分的方法.网格中的区域Cell的宽度是ε正方形(或对于高维时Cell是多面体)，如图1所示，其中一点p的所有join操作的邻居都在相同的Cell里或者直接相邻的Cell里，仅规定相邻的一部分Cell.这样和其他Cell中距离的计算就可以被剪枝掉了.

这种方法很容易用MapReduce来实现.每个Reducer只负责主Cell中的点，并且计算主Cell中点的距离和主Cell中点与邻居Cell中点的距离.通过减少邻居Cell的数量来减少数据的重复计算.进而来代替所有的邻居Cell，每个Reducer只考虑Cell的id等于主Cell格子的id，如图1所示：只考虑深色(绿色)与浅色的Cell).其余的Reducer计算邻居Cell中点与点的距离(C01和C10).但这种方法仍然会计算不必要的计算,例如每个点只与以该点为中心，以2ε为边长的正方形有join结果，其他点的计算是多余的.

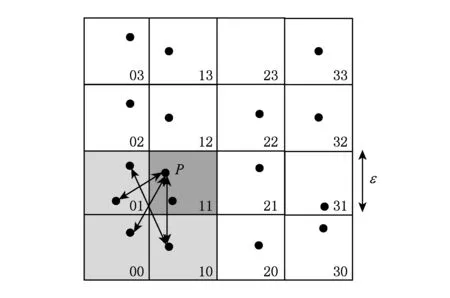
Fig. 1 The grid division.图1 等网格区域划分

可见MRDSJ算法由于存在大量的不必要的计算而降低了它的有效性.在本文中，我们通过采用有效的基于坐标过滤技术来解决这种问题，同时通过内切圆的方法也可以处理聚集的数据，提高了算法的效率.

2 基于MapReduce的坐标过滤和降维技术

2.1 基于MapReduce的坐标过滤技术

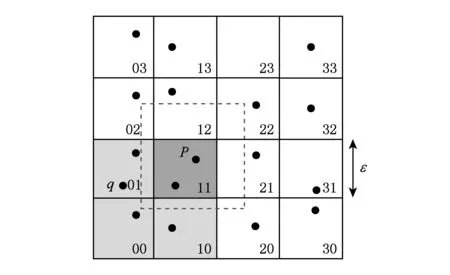
Fig. 2 Reducing the replication calculate.图2 减少重复计算

主要思想是利用滑动窗口的想法，以待处理数据点为中心，以2ε为边长的正方形形成一个滑动窗口，join结果在这个滑动窗口产生，其他点的计算是多余的.基于文献[4]的数据划分的方式，分割成等宽网格的区域Cell.每个Cell中分布着不同的点.主Cell与邻Cell间做相似自连接操作，仅计算id比主Cell的id小的相邻Cell的join操作[4].坐标过滤技术采取同时利用2点的同一维坐标间的距离差与约束ε进行比较，凡是任一维度的坐标差大于约束ε值时，都不再做进一步的join计算.因此减少了候选集对象的数量，如图2所示虚线框(红色)是滑动窗口，所有滑动窗口外的点都不需要与该点进行join计算.如果小于约束ε，则将这2点列入候选集中.

R与R的相似自连接操作定义的表达式见式(2)：

R▷◁εR={(idp,idq)∈R×R|d(datap,

dataq)≤ε}.

(2)

输出结果是集合笛卡儿积的子集，为outdsj∈R×R.idp代表点p所在的Cell的id，datap代表点p的坐标，d(datap,dataq)表示欧几里得距离.

例1. 假设图2中的C11中的点p坐标(3,3)，C01中的点q坐标为(2,2.5)约束ε=2.因为C11和C01在同一个Y维度上，不在同一个X维度上，所以只计算X的坐标差3-2=1<2，即选入候选集.C00中的点坐标为(1.4,1.4)，与点C11中p计算时，X，Y都不在同一个维度.因此都计算2-1.4=0.6, 3.5-1.4=2.1>2，不选入候选集中.

列入候选集后，再进行自连接操作.距离小于阈值的则列入结果集中，得到最终相似对.该方法起到了多重过滤的效果，提高了算法的运行效率，同时也避免了不必要的计算.

算法1. 基于坐标过滤技术.

首次操作，读取INPUT下的所有生成的数据点集，其中包括各个点的原始坐标.为了使数据结构更加清晰明确，输入的点文件格式为JSON格式，从速度性能维度上考虑，数据结构化工具采用业内领先的阿里巴巴的开源工程Fast-Json.

输入：输入文件目录INPUT，占硬盘大小为600 MB，文件数30个，文件内容皆为JSON格式的数据点信息；

输出：输出文件目录OUTPUT，包含所有相似对，其文件数为生成的点所占用的Cell的归档数据数.

mapjob:

①map(LongWritablekey, Textvalue)；

② Pointp=parse(json)；*将文件的数据反序列化成点p*

③ Cellc=getcellbyPoint(p)；*将点坐标转换成Cell坐标，2套坐标系并行处理*

④ 利用算法2根据该cell生成周围5个需要compare的cell集合;

⑤ for (cell:cellList)

⑥write(cell,key);

⑦ endfor

⑧ 利用算法3类似倒排索引，以各个集合为key,该点为value写入到reduce函数.

reducejob:

①reduce(Cellc, Iterable〈Point〉points)

② 通过map传递过来的遍历器去获取点并划分出主Cell和邻Cell这2个集合;

③pmainList=cell.getPoints();

④ for (i:size)

⑤potherList=cell.getOther() ;

⑥ 通过核心算法LessThanE去判别2个点是否距离小于ε;

⑦result.addAll(p1,p2);

⑧ endfor

⑨ boolb=LessThanE(p1,p2);

⑩writer.write(cell).*最后通过不同的Cell归档到不同的结果文件中*

结合整体流程，我们可以知道本算法主要是利用网格区域的划分、坐标的过滤计算及聚集区域的内切圆方法来实现相似自连接操作.

显然算法1的map步的计算复杂性为O(n)，其中n为map的输入;reduce步的计算复杂性为O(n×m)，其中n为reduce的主cell的输入大小，m为reduce的环绕式Cell输入大小加上主Cell的输入大小.

算法2.GenerateAroundcell.

完成网格划分和生成点坐标的二次生成坐标系即为Cell坐标系.通过点p的Cellp所在主Cell坐标系位置compare并generate方法生成邻近的Othercell.MaxX代表点坐标系最大X，而unit代表点坐标系转换Cell坐标系的单位，通过与这2个对比生成需要的围绕式的左侧Cell以及右侧Cell;然后根据步骤①生成的点数去判断是否存在左下Cell;最后分析Cell分布情况 .主Cell的左上也应该纳入对比GenerateAroundCell函数的伪代码如下：

①otherlist=gerateCell(p.x,p.unit);

②list.add(Cell′(p.x-1,p.y));

③list.add(Cell′l(p.x,p.y-1));

④ ifotherlist.size==2

⑤lowerleft=geratelowerleft(p.x,p.unit);

⑥ return;

⑦ endif

⑧list.add=Cell′(p.x-1,p.y-1);

⑨upperleft=gerateupperleft(p.x,p.unit)；

⑩ returnCell′(p.x-1,p.y+1).

通过以上算法生成了环绕式Cell分布集list用作对比主Cell.

将海量数据划分区域，确定Cell周边5个必算(C11和C11,C11和C10,C11和C01,C11和C00,C10和C01的计算)邻Cell后.利用算法3针对每个Cell采用坐标过滤技术进一步剪枝，尽可能少地选定候选集的数目.

容易看出算法2的计算复杂性为O(1).

算法3.lessThanE算法.

由于点的数据集随机分布的特点，对比数据可能出现2个点位于同一坐标的问题，在此视作同一个点不作对比.当主Cell与环绕Cell对比时，根据三角不等式，不在同一维度的，优先对比2点维度的坐标差的绝对值；再与ε做compare，若大于直接过滤掉.当前2步过滤出大部分集合后,继续做自连接操作后的结果与ε作比较，小于的则纳入result集中.lessThanE函数的伪分布代码如下：

① ifcompare(p1.x,p2.x) &&compare(p1.y,p2.y)

② return false；

③ endif

④ if abs(p1.x-p2.x)>ε‖abs(p1.y-p2.y)>ε

⑤ return false；

⑥ endif

⑦ ifpythagorean(p1,p2)<ε

⑨ endif

⑩pythagorean(p1,p2)；

通过以上lessThanE算法即可得出相邻的Cell的符合预期点集合.容易看出算法3的计算复杂性为O(1).

2.2 高维降维方法

对于高维数据，采用了我们提出的新降维技术将高维数据降为2维数据，并且保证相似自连接结果保持在新数据中.我们有下面一个定理.

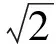
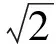
证毕.

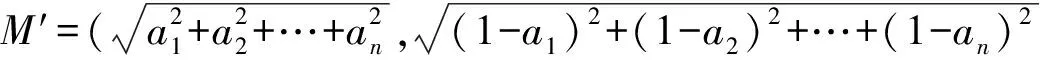
3 聚集区域内切圆算法

3.1 正方形区域划分中的内切圆算法

主要针对主Cell中的点和主Cell中的点之间的自连接操作.为了检测算法可以克服存在聚集数据的特殊情况，我们生成了正态分布的点集合，根据聚类方法找到中心点，以中心点为圆心并以ε2为半径画圆.根据三角形定理，圆内所有点之间的距离都会小于ε，利用算法4进行过滤减枝.如图3所示，利用三角不等式原理：ε2+ε2=ε.因此不必进行圆内的任意2点之间的距离运算，只计算圆外的点之间的距离、圆内点和圆外的点之间的距离.圆内的任意2点之间组成的结果对都在结果集中.

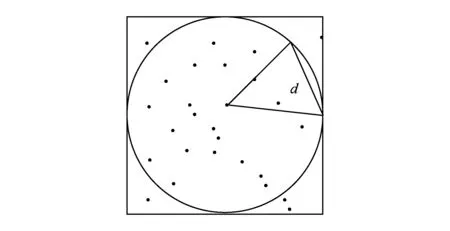
Fig. 3 Dividing gather area.图3 聚集区域划分

定义1. 聚集数据点.一个Cell被称为是聚集点，即Cell中所包含的数据点较多，即数据点个数n较大，例如n>10.

由于数据属于聚集型数据，每个Cell中符合小于ε的点会更加密集，所以单个Cell的优化更为必要.以Cell边长ε为最大直径的内切圆，圆内散布的任何一对点都可以视作距离小于ε.首先取到主Cell的点集,在Cell中寻找聚类中心点.通过compare算法遍历点集与中心点比较,符合条件的加入result集合.将mainlist的点与result点集进行隔离，mainlist剩余的点互相比较生成结果集合，最后主Cell结果集为result.

算法4. 内切圆算法.

输入：聚集分布的数据集；

输出：result1；*相似的结果对*

result2.*内切圆中的点*

①mainlist=cellpoint(c);

②point=cell.center();

③ for (i:mainlist)

④ ifcompare(i,point)<ε2

⑤result2.add(i)；

⑥ endif

⑦ endfor

⑧mainlist.remove(result2)；

⑨ for (i:mainlist)

⑩ for (j:mainlist)

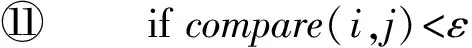
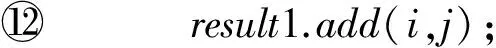
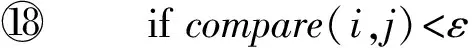
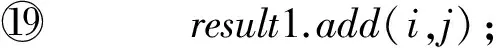
易计算得到内切圆算法的计算复杂性为O(n)+O(m×n+m×m)，其中n为输入的点数，m为Cell中内切圆外的点数.

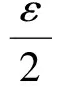
3.2 正六边形区域划分中的内切圆算法

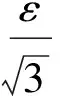
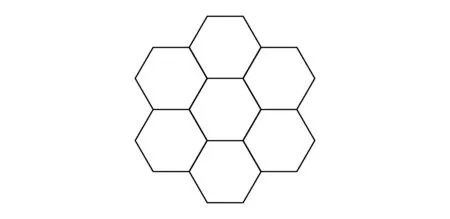
Fig. 4 Hexagonal area region.图4 正六边形区域划分

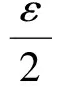
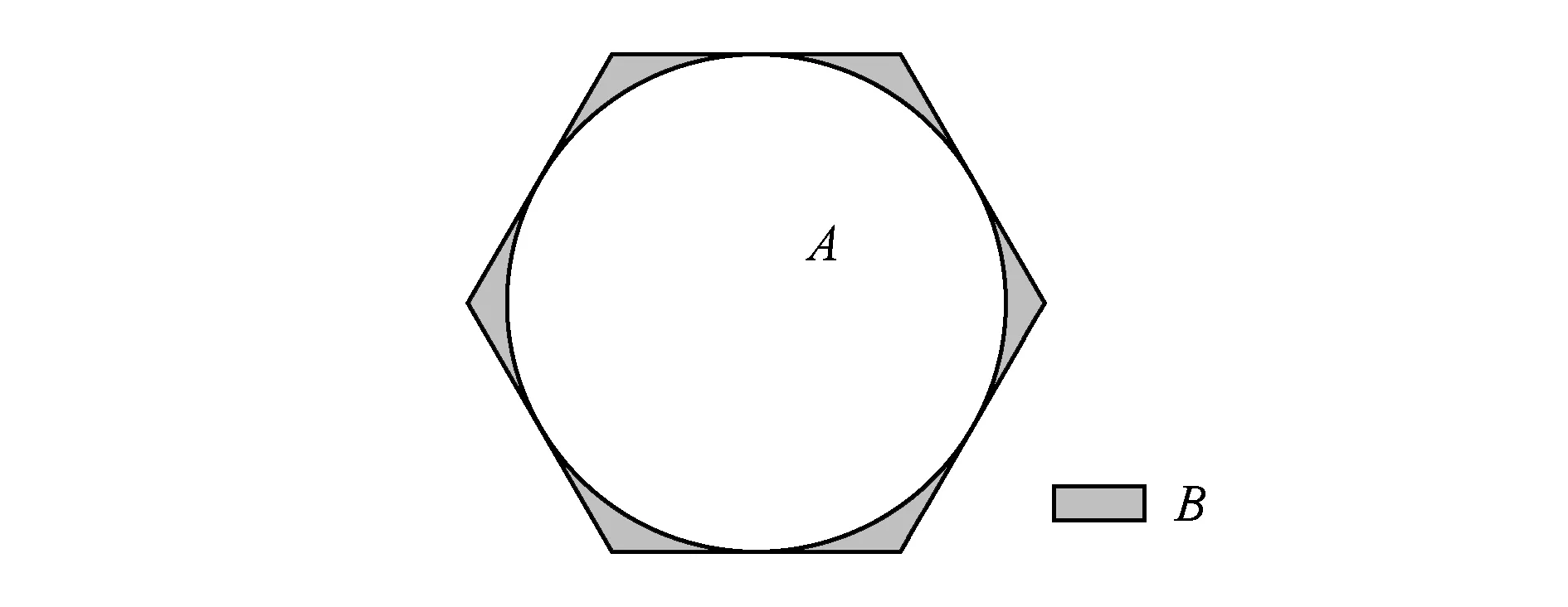
Fig. 5 Hexagon inscribed circle.图5 正六边形内切圆

为了证明正六边形的区域划分方法对于内切圆算法是最优的，我们需要先给出单一形状图形覆盖全平面的概念.单一形状覆盖全平面，是指以大小确定的单一形状图形通过拼接可以无限延伸，并且没有空隙的填满整个全平面，换句话说只有大小相等的一种图形存在,它可以是正多边形，也可以是非正多边形，例如菱形、平行四边形等.

定理2. 在所有单一形状图形覆盖平面的正n边形划分中正六边形是边数最多的.

证明. 正n边形的外角和为2π,我们有外角一定是2πn，所以内角就是π-2πn.由于单一形状图形覆盖平面所以知道都是由同一个形状图形拼接起来的，所以每个顶点一定是由几个正多边形构成，即顶点应该满足：

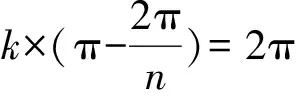
其中,k为自然数.当n=6时，k=3.当n>6时，k=2n(n-2)，上面的方程对于自然数集合无解，所以正六边形是所有单一形状图形覆盖平面的正n边形划分中边数最多的.

证毕.

对于内切圆算法，正n边形划分的算法效率随n的增加而提高,但是由定理2可知，正六边形区域划分是正n边形区域划分中最优的划分.

4 实 验

本节我们对所提出的新算法进行了实验验证，并与基准方案：基于距离的相似自连接(MRDSJ)进行性能对比，MRDSJ采用的基本算法是基于文献[4]提出的一种基于MapReduce框架的算法.我们同时测试了2种算法在并行环境下的性能对比，主要利用合成数据来测试不同数据集大小对执行时间的影响、不同节点数对执行时间的影响及聚集点在正方形划分和正六边形划分时内切圆算法的性能分析.真实生物数据下不同节点数对执行时间的影响.

1) 合成数据——随机产生的向量坐标，数据量为500万、1000万、2000万.坐落在100万个格子中，每个格子10×10，ε=10.用C++编写了正态分布产生函数生成的合成聚集数据为10万、20万、30万个点.

2) 真实数据——采用数据量为200万的DNA序列的生物数据，数据来源于1000 Genome国际项目Sequencing数据[16].

4.1 实验环境

实验是在Mac上实现，硬件环境由8台普通的PC机组成的一个集群，1台为Namenode的机器作为Master，7台为Datanode的机器.节点配置如下：CPU为Q9650 3.00 GHz，Memory为8 GB，Disk为500 GB OS64b Ubuntu12.03 sever.

4.2 实验结果及分析

4.2.1 数据量影响计算距离和执行时间

图6和图7是在节点数为4时3种算法在不同的数据集上的距离计算量和执行时间的结果.从实验数据上可以看出，距离计算量和执行时间都随着数据集的增大而增加.图6显示MRDSJ和PHIDJ算法的距离计算量要比坐标过滤算法距离计算的数量大，原因是坐标过滤算法使用了多种过滤技术如滑动窗口过滤和坐标过滤，剪枝掉了一部分不是结果集的向量对的距离计算.而MRDSJ和PHIDJ仅是网格划分时进行了少量的剪枝，所以正如实验结果所显示，坐标过滤算法产生的距离计算量少.图7显示了在节点数为4时，不同数据集的大小对执行时间的影响.当数据集为500万时，新算法用的时间为460 s，而MRDSJ算法的运行时间为680 s，PHIDJ算法的运行时间为570 s.本文是采用基于坐标过滤的方法，在已有算法的基础上进行优化，使得运行的效率提高.另外，随着数据集的增大，2种算法的运行时间呈增长趋势,并且数据集越大，新算法的效率提高的越多，越节省时间.

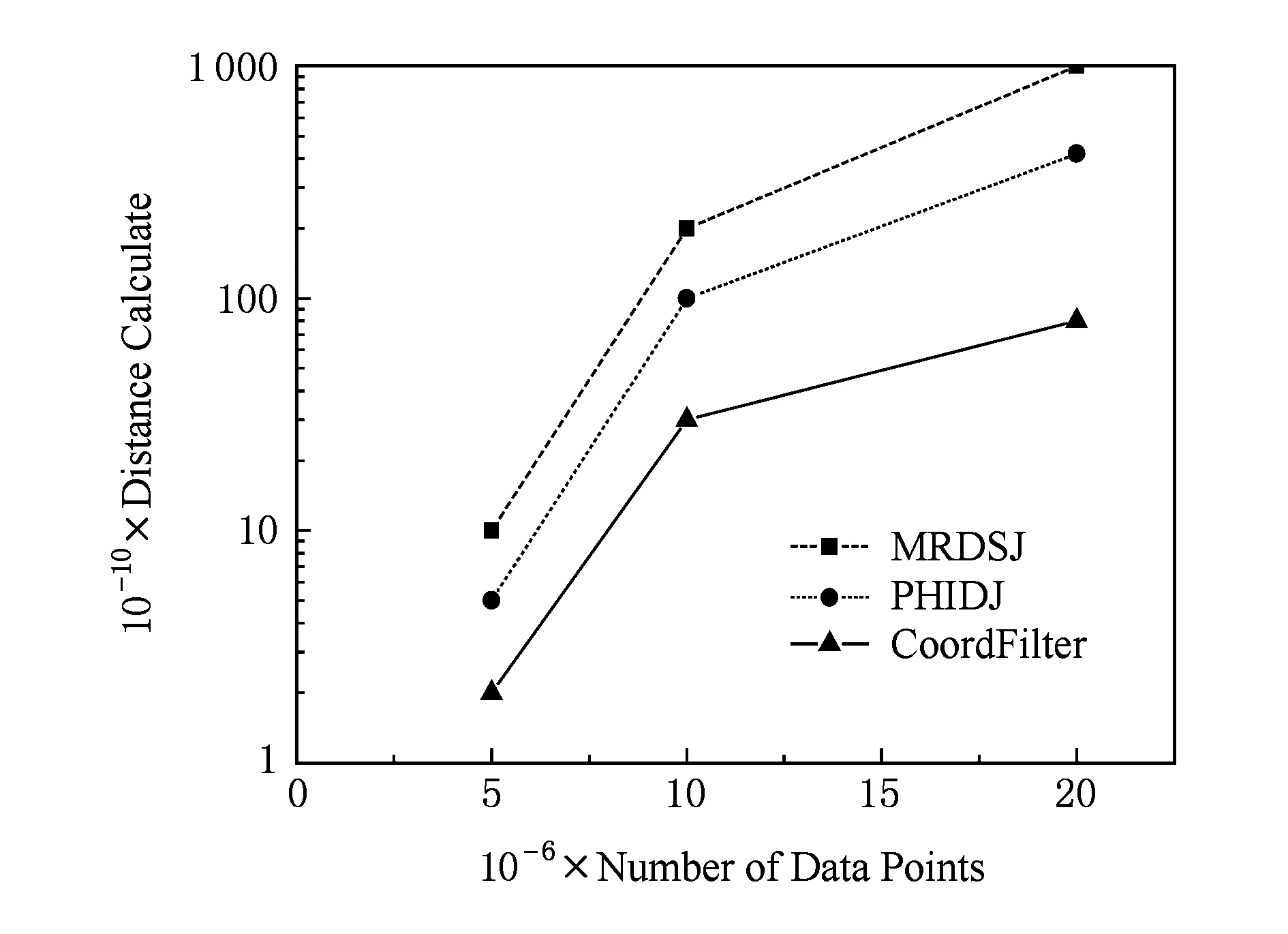
Fig. 6 Impact of different data set size on the distance calculate.图6 数据集大小对距离计算量的影响

Fig. 7 Impact of different data set size on the execution time.图7 数据集大小对执行时间的影响

4.2.2 不同的计算代价对性能的影响

坐标过滤算法整体的计算过程可以分成3个阶段：数据加载阶段(Cd-Load)、滑动窗口过滤阶段(Cd-Slide)和坐标过滤阶段(Cd-Filter).同时实验对比的MRDSJ算法也分为3个阶段：数据加载阶段(Md-Load)、点与Cell边界值过滤(Md-Cells)和点对之间过滤(Md-Pairs).实验结果如图8所示通过不同数据集合的大小，分别对比2种算法在不同计算环节上对算法时间的影响.可见数据加载阶段，2种算法基本相同,因为都是读取数据并进行划分；在滑动窗口过滤阶段坐标过滤阶段的执行时间比MRDSJ的Cell过滤和点对过滤阶段所用的时间短，主要原因是滑动窗口过滤有效地剪枝了周边3个Cell，而Cell边界过滤仅剪枝1个Cell，并且坐标过滤仅计算X或Y维上坐标的差值来过滤，而MRDSJ算法点对过滤是通过计算距离来实现过滤.可见通过对计算代价的分解，可以明显看到坐标过滤算法性能上的提高.

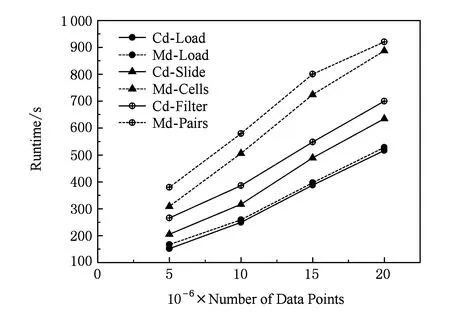
Fig. 8 Impact of different computation cost on performance.图8 不同的计算代价对性能的影响

4.2.3 不同节点数对执行时间的影响

图9(a)展示了针对500万数据集，不同节点数对执行时间的影响.在执行MR-DSJ时，1个节点的运行时间1 440 s，PHIDJ算法的运行时间为1 380 s.本文基于坐标过滤技术的算法，运行时间是1 260 s.说明在伪分布式环境下，该算法仍然可以提高执行速度.当节点数为4时，利用MapReduce强大的并行处理能力，该算法执行时间明显比原有算法少，更加说明该算法的过滤效果明显，减少了通讯代价及成本.

图9(b)则展示了针对1 000万数据集的变化情况.8个节点时MRDSJ算法用了620 s，PHIDJ算法的运行时间为580 s，而基于坐标过滤算法用440 s.8个节点时，由于串行时间的存在，因此并行的执行时间不会由于节点的增多而减少得过少，会有一个下限.但是相比较于更少的节点来说，执行时间还是很短，充分体现了其并行性.

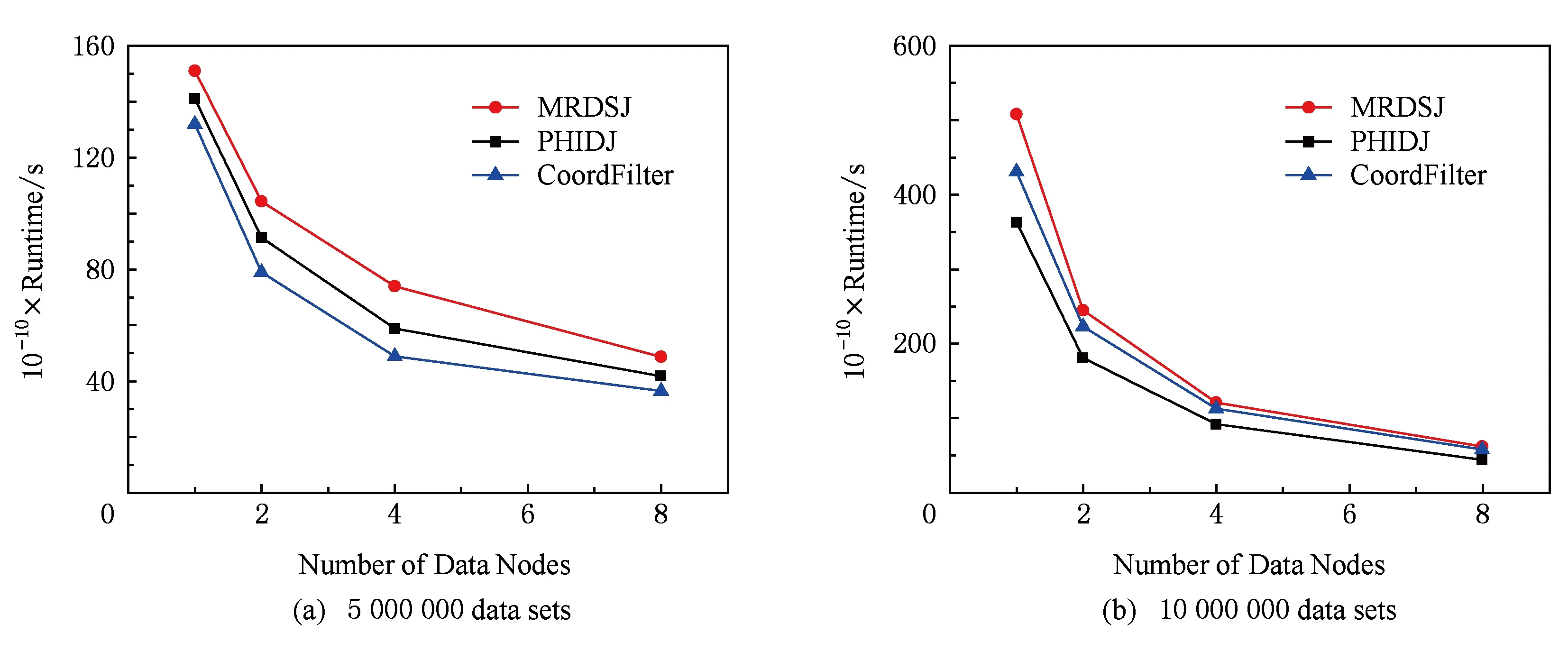
Fig. 9 Impact of different nodes on the execution time.图9 不同节点数下执行时间的对比

从图9(a)(b)对比还可以看出，数据集越大，虽然执行的时间越长，但是随着数据集的增加，算法速度要比数据集少得快，并且节点数越多，效率提高越明显，可能是存在数据高速缓存的原因.我们的算法比原算法的速度更快.

4.2.4 基于聚集区域的Cell性能分析

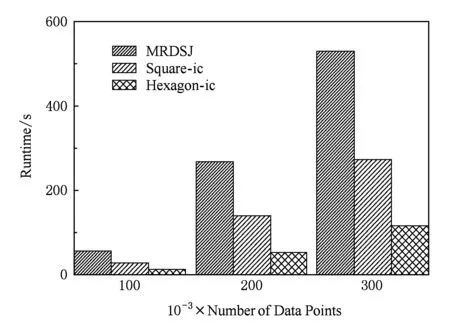
Fig. 10 Impact of different data set size on the execution time.图10 不同数据集大小对执行时间的影响

根据正态分布产生函数生成合成数据为10万、20万、30万个密集点，分布在主Cell中.正方形的内切圆算法利用内切圆算法把区域划分为圆内A部分和圆外B部分.省去B部分的计算，只有A部分及AB部分的运算，因此可以达到如图10所示的结果.在单个Cell中利用正方形内切圆算法(Square-ic)，随着数据量的增加，运行时间也随着增加.但是我们的新算法要比原有算法节省时间，而且数据量越大，算法提高的效率越明显.与原有MRDSJ算法相比较，平均提高了60%以上.而采用六边形区域划分(Hexagonal-ic)的方式，进一步较少了候选集计算的数量，使得内切圆算法比原有MRDSJ算法平均提高了80%以上.

本文采用的是散列存储(Hash storage)结构，为了更全面地对性能进行分析，分别对不同的数据存储方式通过控制变量来验证不同的存储数据结构对性能的影响，通过验证线性存储(liner storage)、随机存储(random storage)以及树状存储(B+tree)的不同存储结构对整体性能的影响，得出实验结果如图11所示.可见，不同的存储结构之间的差异不大，对性能的影响不大.

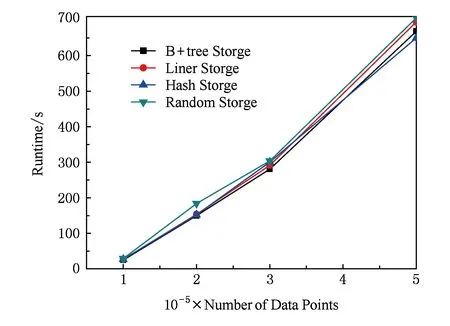
Fig. 11 Impact of different storage structure on performance.图11 不同存储结构对性能影响

4.2.5 真实数据的性能分析

本文采用200万的生物DNA序列，将碱基序列转化成二进制数，每20个碱基字符串为一组，利用滑动窗口得到200万组字符串，进行相似自连接操作获得相近的碱基序列.设A=00，T=01，G=10，U=11，一组字符串平均划分前后2个部分作为坐标参数.相似度设为ε=2，比较不同节点下的运行时间.如图12可以看出同，随着节点数的增加，运行的时间随之减少，但是我们的算法要比MRDSJ算法快.

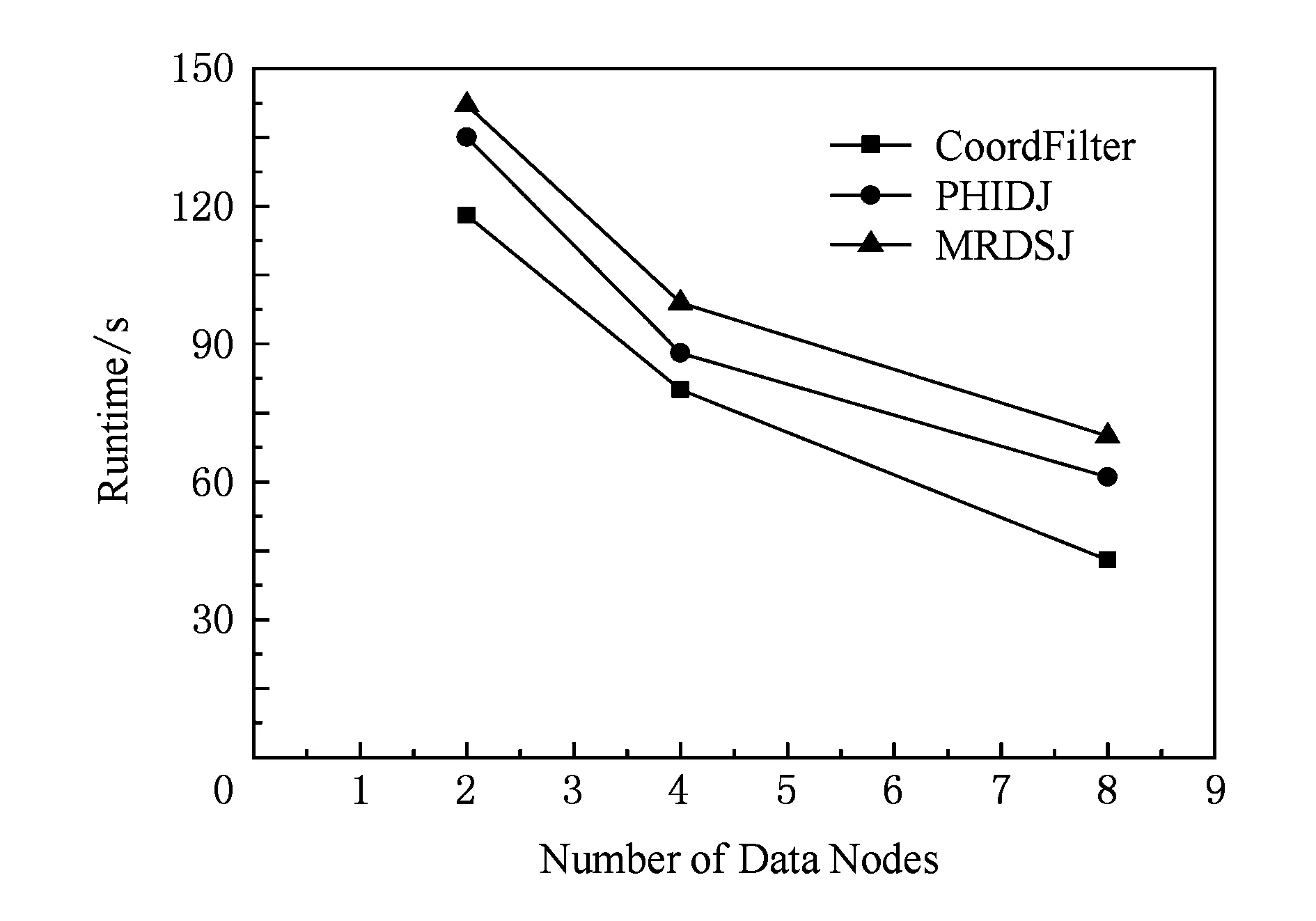
Fig. 12 Impact of different nodes of real data on the execution time.图12 真实数据的不同节点数对执行时间的影响

5 结束语

目前有很多关于相似性连接操作的算法，但是基于距离相似自连接操作的高效算法并不多见.本文在网格划分的基础上使用基于坐标过滤的算法，减少了候选集的数量及不必要的距离计算.同时针对聚集的点，采用内切圆的算法进一步过滤，当采用六边形区域划分时，内切圆的算法效率提高80%以上.未来将研究聚集区域结合高效的聚类算法发现聚集点，并深入研究最优区域划分方法.

[1]Chaudhuri S, Ganti V, Kaushik R. A primitive operator for similarity joins in data cleaning[C] //Proc of the 22nd IEEE Int Conf on Data Engineering. Piscataway, NJ: IEEE, 2006: 5

[2]Wang G, University N. Efficient similarity joins for near duplicate detection[J]. ACM Trans on Data Base Systems, 2008, 36(3): 563-574

[3]Baraglia R, Morales G D F, Lucchese C. Document similarity self-join with MapReduce[C] //Proc of the 10th IEEE ICDM’10. Piscataway, NJ: IEEE, 2010:731-736

[4]Seidl T, Fries S, Boden B. Distance-based self-join for large-scale vector data analysis with MapReduce[C] //Proc of the 15th BTW Conf on Database Systems for Business, Technology, and Web. Magdeburg, Germany: BTW, 2013: 37-56

[5]Pang Jun, Gu Yu, Xu Jia, et al. Research progress of similarity join query [J]. Journal of Frontiers of Computer Science and Technology, 2013, 7(1): 1-13 (in Chinese)(庞俊, 谷峪, 许嘉, 等.相似性连接查询技术研究进展[J]. 计算机科学与探索, 2013, 7(1): 1-13)

[6]Ma Youzhong, Ci Xiang, Meng Xiaofeng. Parallel Top-kjoin on massive high-dimensional vectors[J]. Chinese Journal of Computers, 2015, 38(1): 86-98 (in Chinese)(马友忠, 慈祥, 孟小峰. 海量高维向量的并行Top-k连接查询[J]. 计算机学报, 2015, 38(1): 86-98)

[7]Lu Wei , Shen Yanyan, Chen Su, et al. Efficient processing ofknearest neighbor joins using MapReduce[J]. Proceedings of the VLDB Endowment, 2012, 5(10): 1016-1027

[8]Zhang Chi, Li Feifei, Jestes J. Efficient parallelkNN joins for large data in MapReduce[C] //Proc of the 15th Int Conf on Extending Database Technology. New York: ACM, 2012: 38-49

[9]Silva Y N, Reed J M, Tsosie L M. MapReduce-based similarity join for metric spaces[C/OL] //Proc of the 1st Int Workshop on Cloud Intelligence. New York: ACM, 2012: 1-8 [2015-08-25]. http://dl.acm.org/citation.cfm?doid=2347673.2347676

[10]Blanas S, Patel J M, Ercegovac V, et al. A comparison of join algorithms for log processing in MapReduce[C] //Proc of the 2010 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2010: 975-986

[11]Afrati F N, Ullman J D. Optimizing multiway joins in a MapReduce environment[J]. IEEE Trans on Knowledge and Data Engineering, 2011, 23(9): 1282-1298

[12]Wang Wei, Qin Jianbin, Xiao Chuan, et al. VChunkJoin: An efficient algorithm for edit similarity joins[J]. IEEE Trans on Knowledge and Data Engineering, 2013, 25(8): 1916-1929

[13]Song Ge, Rochas J, Huet F, et al. Solutions for processingknearest neighbor joins for massive data on MapReduce[C] //Proc of the 23rd Int Conf on Parallel, Distributed and Network-Based Processing. Piscataway, NJ: IEEE, 2015: 279-287

[14]Li Tiantian, Yu Ge, Guo Chaopeng, et al. Multi-way join optimization approachbased on MapReduce[J]. Journal of Computer Research and Development, 2016, 53(2): 467-478 (in Chinese)(李甜甜, 于戈, 郭朝鹏, 等. 基于MapReduce的多元连接优化方法[J]. 计算机研究与发展, 2016, 53(2): 467-478)

[15]Fries S, Boden B, Stepien G, et al. PHIDJ: Parallel similarity self-join for high-dimensional vector data with MapReduce[C] //Proc of the 30th Int Conf on Data Engineering .Piscataway, NJ: IEEE, 2014: 796-807

[16]Abecasis G R, Adam A, Brooks L D, et al. An integrated map of genetic variation from 1,092 human genomes.[J]. Nature, 2012, 491(7422): 56-65Bao Guanghui, born in 1991. Master candidate. Her main research interests include analysis and mining on massive data.

Zhang Zhaogong, born in 1963. Professor and MSc supervisor. His main research interests include massive data mining and bioinformatics, etc.

Li Jianzhong, born in 1950. Professor and PhD supervisor. His main research interests include massive data management and computing, wireless sensor network, ect.

Xuan Ping, born in 1979. PhD and associate professor. Her main research interests includes massive data mining and bioinformatics.

Novel MapReduce-Based Similarity Self-Join Method: Filter and In-Circle Algorithm

Bao Guanghui1, Zhang Zhaogong1, Li Jianzhong1,2, and Xuan Ping1

1(School of Computer Science and Technology, Heilongjiang University, Harbin 150080)2(SchoolofComputerScienceandTechnology,HarbinInstituteofTechnology,Harbin150001)

Similarity self-join is a very important study in many applications. For the massive data sets, MapReduce can provide an effective distributed computing framework, in particular, similarity self-join can be applied on the framework. There are still problems, such as fine partition method, are applied to cluster data area for load balancing, but it is not easy to implement. Existing algorithms can’t effectively accomplish similarity self-join operations for the massive data sets. In this paper, we propose two novel algorithms of similarity self-join on the MapReduce framework, and use coordinate-filtering techniques to get the valid candidate sets and use the in-circle method on the hexagon-based partition area. Those coordinate-filtering techniques are based on equal-width grid partition, and adopt the restriction that two points have more distances than two projective points in the same axis, and can drop obviously some candidate set. We also proof that the hexagon-based partition is the best form in all normal partition. Our experimental results demonstrate that the novel method has an advantage over the other join algorithms for cluster data area which improves efficiency over 80%. The algorithm can effectively solve the problem of the similarity self-join for the massive data in cluster data area.

massive data sets; filter; similarity self-join; data partition; Hadoop platform; MapReduce programming model

2015-09-01；

2016-05-03

国家“九七三”重点基础研究发展计划基金项目(2012CB316200)；国家自然科学基金项目(61302139) This work was supported by the National Basic Research Program of China (973 Program) (2012CB316200) and the National Natural Science Foundation of China (61302139).

张兆功(zhaogong.zhang@qq.com)

TP311.13