Consensus of single integrator multi-agent systems with directed topology and communication delays

Xiang XU,Lu LIU,Gang FENG

Department of Mechanical and Biomedical Engineering,City University of Hong Kong,Kowloon,Hong Kong,China Received 27 November 2015;revised 15 December 2015;accepted 15 December 2015

Consensus of single integrator multi-agent systems with directed topology and communication delays

Xiang XU,Lu LIU,Gang FENG†

Department of Mechanical and Biomedical Engineering,City University of Hong Kong,Kowloon,Hong Kong,China Received 27 November 2015;revised 15 December 2015;accepted 15 December 2015

In this paper,a distributed control scheme has been developed for consensus of single integrator multi-agent systems with directed fixed communication topology for arbitrarily large constant,time-varying or distributed communication delays.It is proved that the closed loop control system can reach consensus with an exponential convergence rate if and only if the topology is quasi-strongly connected.Simulation results are also provided to demonstrate the effectiveness of the proposed controller.

Consensus,directed fixed topology,single integrator multi-agent systems,communication delays

1 Introduction

In the past years,multi-agent systems have become a very popular topic in the control community due to its wide applications in many areas,e.g.,multiple spacecraft vehicles[1],biological systems[2],mobile robots[3],formation control[4],flocking[5]and so on.Consensus is a typical problem of multi-agent systems and also has been widely studied.In many applications involving multi-agent systems,groups of agents need to reach an agreement on certain quantities of interest whileeachagenthasonlyaccesstotheinformationofits neighboring agents.Some typical results on consensus of multi-agent systems can be found in[6-10].

Time-delays are inherent features of practical systems,which are often the main cause for instability and poor performance.The consensus problem of multiagent systems with time-delays has also been studied in the past years.A couple of consensus protocols for discrete-time multi-agent systems with time-delays were provided in[11-13].In[14]and[15],continuoustime multi-agent systems with a single time-varying delay were considered.It is worth pointing out that most of the existing works consider constant time-delays or a single time-delay.This motivates us to consider more general models of time-delays.

This paper mainly addresses the consensus problem of single integrator multi-agent systems with directed fixed communication topology for arbitrarily large constant,time-varying or distributed communication delays.In[16],a consensus protocol was proposed for single integrator multi-agent systems with time-delays and it was proved the closed loop control system is asymptotically stable.In this paper,we proposed a new control scheme.We prove that the closed loop control system can reach consensus with an exponential convergence rate.Furthermore,we provide an example to show that if the control gain is asymmetric,the system may not reach consensus.

The rest of this paper is organized as follows.In Section 2,we introduce some basic concepts and preliminaries.In Section 3,we consider the consensus problem of single integrator multi-agent systems and present our main results.Simulations are provided in Section 4 and conclusions are drown in Section 5.

2 Preliminaries

2.1 Notations

Throughout this paper,the following notations are used.‖·‖denotes the Euclidean norm of vectors and induced 2-norm of matrices.diag{a1,a2,...,an}is a diagonal matrix with diagonal elements a1,a2,...,an.Furthermore,inf and sup denote the infimum and supremum of a set,respectively.

2.2 Graph theory

2.3 Problem statement

We consider a single integrator multi-agent system consisting of N agents with dynamics

where xi(t)∈Rnand ui(t)∈Rnare the state and control input of agent i,respectively.We propose a controller as follows:

where K ∈ Rn×nis the control gain and is assumed to be symmetric and Hurwitz,Tij(xj)is a delay operator that indicates the delayed information of xjdue to communication and will be further explained later.The system is said to reach consensusto avoid confusion,we denote thatThus we can obtain the controlled i system as follows:

Tij(xj)is a delay operator which can represent three most common delay operators as in[16]:constant delays Tij(xj)=xj(t- τij),τij∈ [0,T],time-varying delays Tij(xj)=xj(t- τij(t)),τij:R → [0,T],where τij(t)is piecewise continuous and has a dwell time τ,and distributed delays,with delay

3 Consensus of single integrator multiagent systems

3.1 Main results

First,we introduce the following coordinate transformation.Since K is symmetric and Hurwitz,there exists an orthogonal matrix P ∈ Rn×nsuch that K=P-1ΛP,where Λ =diag{-λ1,-λ2,...,-λn}and-λk＜ 0,k=1,2,...,n is the eigenvalue of K.Let zi(t)=Pxi(t),we have

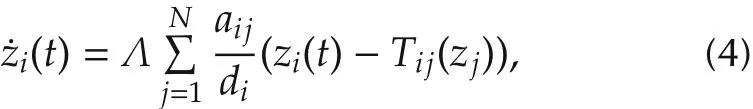
We can see that system(3)achieves consensus if and

Lemma 1The interval Υk(t)and its lengthare non-increasing for system(4),for all dimensionsk=1,2,...,n.

ProofIt follows from system(4)thatzi[k]satisfies the equation

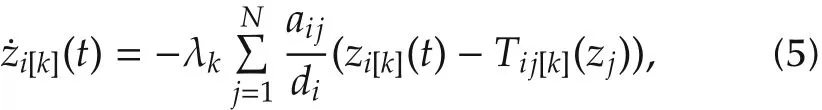
where λk＞ 0.It can be also proved thatTij[k](zj)∈ Υk(t).It is easily obtained thatzi[k]is piecewise continuously differentiable.The statement that Υk(t)is non-increasing is equivalent tois non-increasing andis nondecreasing.We first prove thatis non-increasing.According to the definition ofit can only increase attimetifthereisanagentisuchthatzi[k](t)=and ifzi[k](t)is increasing.However,ifzi[k](t)=thenwhich meanszi[k]is not increasing.Therefore,is non-increasing.With the similar argument,we can also prove thatis non-decreasing,and thus Υk(t)is non-increasing,for anyk=1,2,...,n. □

Theorem 1The controlled multi-agent system(3)consisting ofNagents with directed fixed topology can achieve consensus if and only if the communication topology is quasi-strongly connected.Furthermore,there existx0∈ Rnand β ＞ 0 such that‖xi-x0‖≤C(t0)e-β(t-t0),whereC(t0)is a constant depending on initial conditions.

Proof(Sufficiency) We only need to show the consensus of system(4).In Lemma 1,we have already shown that Υk(t)is non-increasing.If every Υk(t)contracts to a single point,or in other wordfor allk=1,2,...,n,whereis the length of the interval,then the system will achieve consensus.In the sequel,it will be shown that,for any initial timet0≥0 and δ＞0

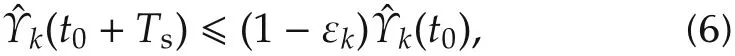
whereTs=(N-1)(T+δ)+T,Nis the number of agents and εk＞ 0.

It can be seen that the communication topology has a spanning tree.Assume agenti0is the root of the spanning tree.Define a sequence of setsL0⊆L1⊆L2...⊆LN-1⊆N={1,2,...,N},whereL0={i0}.Forl≥1,we defineLl=Ll-1∪{il|∃il-1s.t.il-1∈ Nil}.Inotherwords,Llis the set of all agents that the signal ofi0will reach through at mostledges.It is obvious thatLN-1=N.

For agenti0at timet0,assume thatWe will prove inequality(6)by the following iteration.

Fori0∈L0,t≥t0,λk＞ 0,

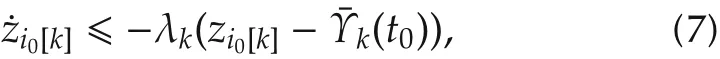
which is due to the fact thatis non-increasing andUsing the comparison principle,we can get that for allHence,[-T,0].It is noted that for agenti0,it is possible thatdi0=0,but the result in this situation also holds.

Thus,for alli1

Forzi1[k](t)≤¯Υk(t0)and with the comparison princi-We can also find that this equation also holds for alli∈L1.

With the similar discussion,it can be also obtained

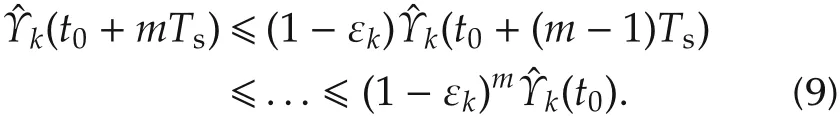
Therefore,for any given

(Exponential convergence) We will further prove that system(3)achieves consensus with an exponential convergence rate under the quasi-strongly connected assumption.Accordingtothepreviousproof,wealready have

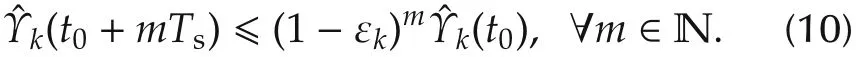
(Necessity) Inthecontrolledmulti-agentsystem(3),the state of agentican affect the state of agentjif and only if there is a directed path fromitoj.If the directed graphGdoes not have a spanning tree,then there exist at least two agents who cannot affect each other.That means,it is impossible for the two agents to reach consensus.Necessity is thus proved. □

Remark 1LetK=I,the controlled system(3)reduces to that in[16]in the case of a fixed topology.In[16],the system is proved to reach consensus asymptotically.In this paper,we further prove that the system can reach consensus with an exponential convergence rate β.

Remark 2The convergence rate β is a continuous function of δ＞0.Moreover,it can be seen thatwhich implies that β has a maximal value corresponding to δ with givenTandK.

3.2 Some discussions

In this section,we consider the following controlled single integrator multi-agent system consisting of two agents:

wherex1,x2∈ Rn,andK∈ Rn×nis a Hurwitz matrix.It has been already proved in the last section that,ifKis symmetric and Hurwitz,the system can reach consensus,In this section,we further consider the case thatKis asymmetric.

Lete=x1-x2,the system(13)can reach consensus if and only ifIt can be derived from the system dyna

mics that˙e=K(e+e(t-τ)).Using the frequency domain analysis,it is easy to obtainE(s)=Gτ(s)e(0),whereGτ(s)=Z-1τ=(sI-K(1+e-sτ))-1.Thusand only if all zeros ofZτare located on the open left-half complex plane.The zeros ofZτ(s)can be described by the following equation:

Suppose-λ1,-λ2,...,-λnare eigenvalues ofK,then the zeros ofZτ(s)satisfies

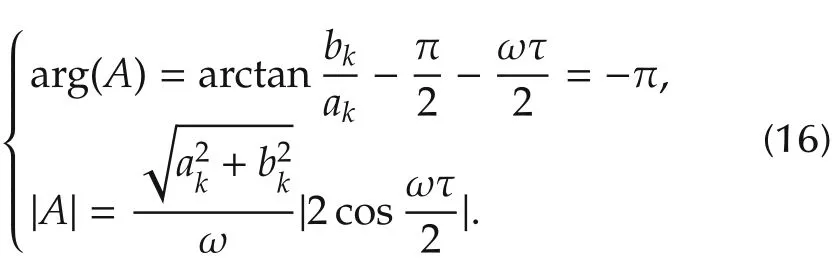
From the first equality we can get cotand thusSince(A,0)is the leftmost intersection node andbk＞0,from Fig.1Thuswhich leads to the situation that the net encirclement of the Nyquist plot of Γk(s)around-1 is not zero ifbkis sufficiently large,i.e.,the controlled system(13)cannot reach consensus.

WhenKis symmetric,which impliesbk=0,thenA=0,which means the net encirclement of the Nyquist plot of Γk(s)around-1 is zero,i.e.,the controlled system(13)can reach consensus in this situation.It is in accordance with the result of Theorem 1.

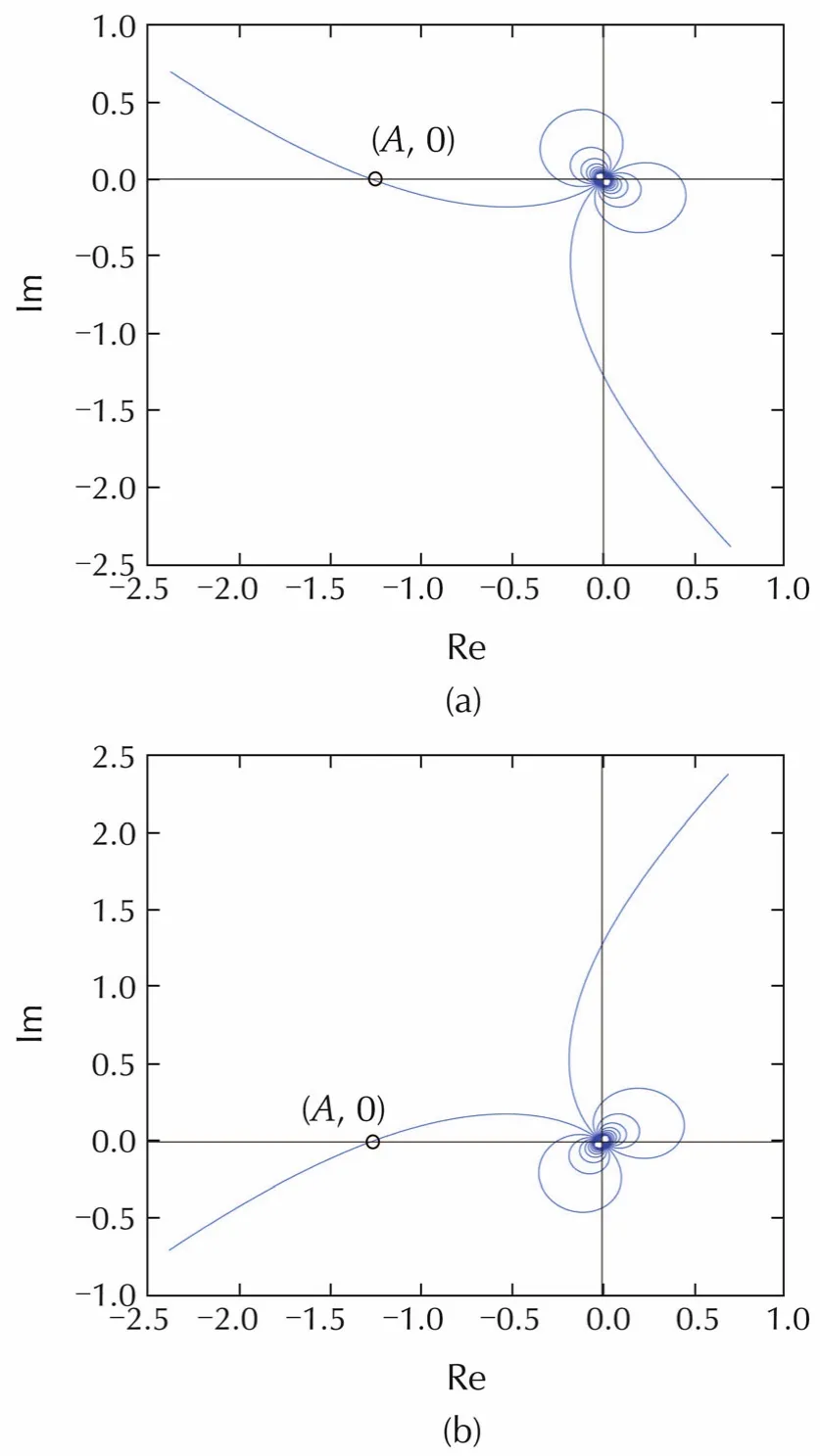
Fig.1 Sketch of Nyquist plot of Γk(jω).(a)bi＞ 0.(b)bi＜ 0.

Remark 3It follows from the discussions that if the control gainKis not symmetric,the controlled system(13)may not reach consensus.However,it can also be seen that if the imaginary parts of the eigenvalues of asymmetric matrixKare sufficiently small,the controlled system(13)can still reach consensus.

4 Simulation examples

Consider a single integrator multi-agent system consisting of 4 agents.The communication topology is shown in Fig.2 and the adjacency matrix is given as follows:

Fig.2 Communication topology consisting of 4 agents.

easily verified that the chosen matrixKis symmetric and Hurwitz.

i)Forconstantdelays,weassumethatτ13=0.5,τ14=0.6,τ21=0.2,τ31=1,τ32=0.3,τ41=0.4.Fig.3 shows the first dimensions of the corresponding state responses.

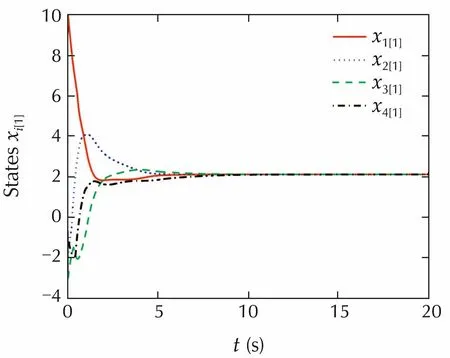
Fig.3 The first dimensions of state responses with constant delays.

ii)For time-varying delays,we assume that τ13(t)=1+0.5sint,τ14=1.2+0.6sint,τ21=0.4+0.2sint,τ31=2+sint,τ32=0.6+0.3sint,τ41=0.8+0.4sint.Fig.4 shows the first dimensions of the corresponding state responses.

iii)For distributed delays,we assume thatFig.5 shows the first dimensions of the corresponding state responses.

Figs.3-5 clearly demonstrate the effectiveness of the proposed controller.

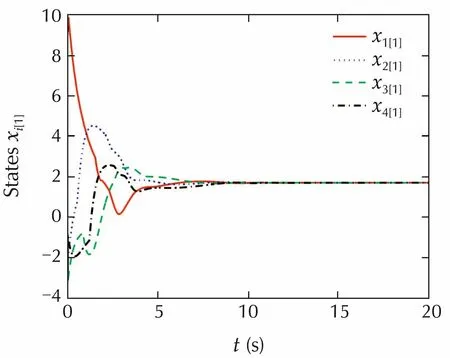
Fig.4 The first dimensions of state responses with time-varying delays.

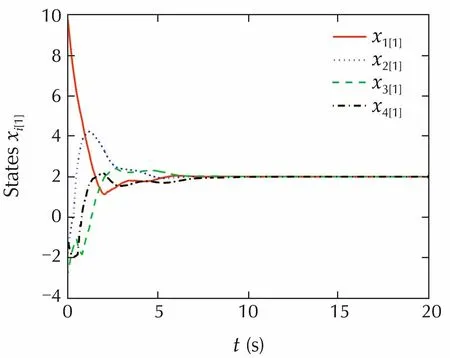
Fig.5 The first dimensions of state responses with distributed delays.

5 Conclusions

This paper considered the consensus problem of single integrator multi-agent systems with directed fixed communication topology for constant,time-varying or distributed communication delays.A distributed control protocol was proposed,and it was shown that the controlled single integrator multi-agent system can reach consensus if and only if the communication topology is quasi-strongly connected.In addition,a special case was provided to show that the controlled system may not achieve consensus if the control gain is not symmetric.Simulations were given to illustrate the effectiveness of the proposed controller.

[1]W.Ren.Formation keeping and attitude alignment for multiple spacecraft through local interactions.Journal of Guidance,Control,and Dynamics,2007,30(2):633-638.

[2]S.Martinez,J.Cortes,F.Bullo.Motion coordination with distribution information.IEEE Control Systems Magazine,2007,27(4):75-88.

[3]Y.U.Cao,A.S.Fukunaga,A.Kahng.Cooperativemobilerobotics:Antecedents and directions.Autonomous Robots,1997,4(1):7-27.

[4]F.Xiao,L.Wang,J.Chen,et al.Finite-time formation control for multi-agent systems.Automatica,2009,45(11):2605-2611.

[5]R.Olfati-Saber.Flocking for multi-agent dynamic systems:Algorithms and theory.IEEE Transactions on Automatic Control,2006,51(3):401-420.

[6]A.Jadbabaie,J.Lin,A.S.Morse.Coordination of groups of mobile autonomous agents using nearest neighbor rules.IEEE Transactions on Automatic Control,2003,48(6):988-1001.

[7]L.Moreau.Stability of multiagent systems with time-dependent communication links.IEEE Transactions on Automatic Control,2005,50(2):169-182.

[8]R.Olfati-Saber,R.M.Murray.Consensus problems in networks of agents with switching topology and time-delays.IEEE Transactions on Automatic Control,2004,49(9):1520-1533.

[9]R.Olfati-Saber,J.A.Fax,R.M.Murray.Consensus and cooperation in networked multi-agent systems.Proceedings of the IEEE,2007,95(1):215-233.

[10]W.Ren,R.W.Beard.Consensus seeking in multiagent systems under dynamically changing interaction topologies.IEEE Transactions on Automatic Control,2005,50(5):655-661.

[11]F.Xiao,L.Wang.Consensus protocols for discrete-time multiagent systems with time-varying delays.Automatica,2008,44(10):2577-2582.

[12]P.Lin,Y.Jia.Consensus of second-order discrete-time multiagent systems with nonuniform time-delays and dynamically changing topologies.Automatica,2009,45(9):2154-2158.

[13]C.Tan,G.Liu.Consensus of discrete-time linear networked multi-agent systems with communication delays.IEEE Transactions on Automatic Control,2013,58(11):2962-2968.

[14]P.Lin,Y.Jia.Average consensus in networks of multi-agents with both switching topology and coupling time-delay.Physica A:Statistical Mechanics and its Applications,2008,387(1):303-313.

[15]J.Hu,Y.Hong.Leader-following coordination of multi-agent systems with coupling time delays.Physica A:Statistical Mechanics and its Applications,2007,374(2):853-863.

[16]U.M¨unz,A.Papachristodoulou,F.Allg¨ower.Consensus in multiagent systems with coupling delays and switching topology.IEEE Transactions on Automatic Control,2011,56(12):2976-2982.

[17]C.Godsil,G.F.Royle.Algebraic Graph Theory.New York:Springer,2013.

DOI10.1007/s11768-016-5122-x

†Corresponding author.

E-mail:megfeng@cityu.edu.hk.Tel.:+852 3442 5900.

This work was supported by the Research Grants Council of the Hong Kong Special Administrative Region of China(No.CityU/11203714).©2016 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg

the Bachelor of Engineering degree in Automation from Nanjing University of Science and Technology,China in 2014.He is currently working towards the Ph.D.degree at City University of Hong Kong,Hong Kong.His research interests include multi-agent systems and time-delay systems.E-mail:xiangxu5-c@my.cityu.edu.hk.

Lu LIUreceived her Ph.D.degree in 2008 in the Department of Mechanical and Automation Engineering,Chinese University of Hong Kong,Hong Kong.From 2009 to 2012,shewasanAssistantProfessorinUniversity of Tokyo,Japan,and then a Lecturer in University of Nottingham,United Kingdom.She is currently an Assistant Professor in the Department of Mechanical and Biomedical Engineering,City University of Hong Kong,Hong Kong.Her research interests are primarily in networked dynamical systems,control theory and applications,and biomedical devices.She received the Best Paper Award(Guan Zhaozhi Award)in the 27th Chinese Control Conference in 2008.E-mail:luliu45@cityu.edu.hk.

Gang FENGreceived the B.Eng and M.Eng.degrees in Automatic Control from Nanjing Aeronautical Institute,China in 1982 and in 1984 respectively,and the Ph.D.degree in Electrical Engineering from the University of Melbourne,Australia in 1992.He has been with City University of Hong Kong since 2000 where he is now Chair Professor of Mechatronic Engineering.He was lecturer/senior lecturer at School of Electrical Engineering,University of New South Wales,Australia,1992-1999.He was awarded an Alexander von Humboldt Fellowship in 1997,and the IEEE Transactions on Fuzzy Systems Outstanding Paper Award in 2007,and Changjiang chair professorship from Education Ministry of China in 2009.His current research interests include multi-agent systems and control,intelligent systems and control,and networked systems and control.Prof.Feng is an IEEE Fellow,an associate editor of IEEE Trans.Fuzzy Systems and Journal of Systems Science and Complexity,and was an associate editor of IEEE Trans.Automatic Control,IEEE Trans.Systems,Man&Cybernetics,Part C,Mechatronics,and Journal of Control Theory and Applications.E-mail:megfeng@cityu.edu.hk.