Matrix expression and vaccination control for epidemic dynamics over dynamic networks

Peilian GUO,Yuzhen WANG

School of Control Science and Engineering,Shandong University,Jinan Shandong 250061,China Received 11 October 2015;revised 14 October 2015;accepted 14 October 2015

Matrix expression and vaccination control for epidemic dynamics over dynamic networks

Peilian GUO†,Yuzhen WANG

School of Control Science and Engineering,Shandong University,Jinan Shandong 250061,China Received 11 October 2015;revised 14 October 2015;accepted 14 October 2015

This paper investigates epidemic dynamics over dynamic networks via the approach of semi-tensor product of matrices.First,a formal susceptible-infected-susceptible epidemic dynamic model over dynamic networks(SISED-DN)is given.Second,based on a class of determinate co-evolutionary rule,the matrix expressions are established for the dynamics of individual states and network topologies,respectively.Then,all possible final spreading equilibria are obtained for any given initial epidemic state and network topology by the matrix expression.Third,a sufficient and necessary condition of the existence of state feedback vaccination control is presented to make every individual susceptible.The study of illustrative examples shows the effectiveness of our new results.

Epidemic dynamics,dynamic network,vaccination control,semi-tensor product of matrices

1 Introduction

Since ancient times,the health of human beings has always been seriously threatened by many kinds of infectious diseases,such as black death,SARS,H1N1 influenza and MERS.Due to the complex and ubiquitous social interaction networks,once an epidemic outbreaks,the disease is likely to widely spread and causes much loss.Thus,epidemic dynamics over networks has recently been studied widely[1-3].

In the existing literatures,there are two parallel studies on epidemic dynamics with social contacts.One is the dynamics on networks,that is,the evolutionary of individual states.Based on the static network,many researchers have studied the spreading features of individual disease states,for example,the absence of epidemicthresholdsonscalefreenetworks[1,4].Theother one is the dynamics of networks.Scholars have devoted their efforts to the research of temporal network,whose edges are active and changed according to simple dynamical rules,such as preferential attachment or selective rewiring[5].While most people have for a longtime been concerned with the separate study of the two aspects,the investigation of adaptive networks has in recent years received a rapidly increasing amount of attention,with many applications in social,biological,and technical systems[6-9].The adaptive network dynamics takes the feature of real world into account,namely,the ability to adapt the network graph dynamically in response to the dynamics of individual states.

In this paper,we mainly investigate an epidemic spreading model over dynamic social networks(see Fig.1),where individuals tend to respond to the emergence of an epidemic by avoiding contacts with infected individuals.Such rewiring of local connections can prevent or slow down the spread of the disease,but may not eliminate the disease.To our best knowledge,most of the existing results on epidemic dynamics are mainly basedoncomputersimulationandstatistics.Itisdifficult to establish a rigorous mathematical model to analyze,predict and control the SISED-DN directly.Therefore,we need develop new techniques to investigate the epidemic spread.

Fig.1 The interaction dynamics of individual states X(t)and network topologies A(t).

It should be pointed out that the local social contacts among a finite population are finite.Thus,the SISEDDN can be naturally described by logical dynamical networks,which have been studied perfectly by a powerful analysis tool named semi-tensor product of matrices(STP).The method has been well established by Cheng[10].Up to now,it has been successfully applied to many areas,including the analysis and control of logical networks[11-15],the coloring problem[16,17],finite automata[18],the fault detection[19,20],potential game[21]and evolutionary networked game[22-25].

Motivated by the above,we use the STP framework to investigate the SISED-DN.The main contributions of this paper are as follows:i)the matrix expression is established for the SISED-DN,based on which we can predict all possible final spreading equilibria,and ii)a necessary and sufficient condition is presented for the existence of state feedback vaccination control problem to make all individuals susceptible.Illustrative examples show that the condition is effective and one can easily check the condition with the help of MATLAB toolbox.

Therestofthispaperisorganizedasfollows.Section2 contains the preliminaries on the semi-tensor product of matrices.Section3 establishes the matrix expression of the SISED-DN.The final spreading equilibria and vaccination control are investigated in Section4.Illustrative examples are given to support our new results,which is followed by a brief conclusion in Section5.

NotationsRn×mdenotes the set of alln×mreal matrices.The setcolumn of the identity matrixIk.A matrixM∈ Rk×tis called a logical matrix,if the columns set Col(M)⊆ Δk.Denote the set ofk×tlogical matrices by Lk×t.For a matrixbriefly asColi(A)(Rowi(A))denotes theith column(row)ofA.

2 Preliminaries

In this section,we recall some necessary preliminaries on the STP of matrices,which is a basic tool used in this paper.Please refer to[10]for more details.

The semi-tensor product of matrices is defined as follows.

De fi nition 1[10] LetA∈ Rm×nandB∈ Rp×q,and τ=lcm(n,p)is the least common multiple ofnandp.The semi-tensor product(STP)ofAandBis defined as

where⊗is the Kronecker product.

It is noted that whenn=p,AB=AB.Thus,the STP of matrices is a generalization of the conventional matrix product,which makes the product of two arbitrary matrices well defined.All the main properties of conventional matrix product remain true.Throughout this paper,the default matrix product is STP,and the symbol“”is mostly omitted without confusion.

In the following,we list some special properties of STP of matrices,which will be used in the sequel.

i)LetX∈ Rt×1be a column vector andA∈ Rm×n.Then

ii)LetX∈ Rm×1andY∈ Rn×1be two column vectors.

Then

v)LetxiThen we have1,2,...,n.

The STP of matrices is convenient in dealing with finite-value(logical)functions by expressing them into algebraic forms.The following lemma shows the matrix expression of Boolean functions.

Lemma 1[10]Letf:be a Boolean function.Then,identifying 1∼and 0∼,there exists a unique matrixMf∈ L2×2n,called the structural matrix off,such that

3 Matrix expression of SIS epidemic dynamics over dynamic networks

In this section,using the STP approach,we establish the matrix expression of epidemic dynamics over dynamic networks.In Section3.1,a formal SISED-DN is presented.Sections3.2 and 3.3 give the matrix expression for the dynamics of individual states and network topologies,respectively.

3.1 SIS epidemic dynamic model

This part presents a formal SIS epidemic dynamic model over dynamic networks,where the susceptible individuals are able to avoid contacting with the infected individuals by rewriting their network connections.

A formal SISED-DN generally consists of four basic components:

i)nsocial individuals,whose states are either susceptible(S)or infected(I).xi(t)∈{S,I}is the state of individualiat timet,andX(t)=(x1(t),x2(t),...,xn(t)).For convenience,we use“0"to express the state“S”and use “1"to express the state “I".Denote the individual set byN={1,2,...,n}.

ii)A time varying network topology,described by an undirected graph=(V,(t)),where V=Ndenotes the individual set,and(t)={(i,j)|i,j∈V,i≠j}denotes the social link between pairs of individuals at timet,satisfying(i,j)=(j,i).The adjacent matrix of G at timetis

iii)The dynamics of individual states:At each period,susceptible individuals may become diseased due to the social interaction with their infected neighbors,and the infected individual with immune ability may recover from the disease,becoming susceptible.

iv)The dynamics of network topologies:For every SI link(connecting an infected individual with a susceptible),the susceptible is able to break the link to the infected,and forms a new link to another unconnected individual.Doubleconnectionsandself-connectionsare not allowed to form in this way.

Because there exists a dynamic exchange of information,the evolution of network topology depends on the state of individuals in some period,and in turn affects the spreading dynamics of individual states.Such a feature makes an interactional feedback loop be created.

Based on the above SISED-DN,the interactional dynamics between network topology and individual state can be expressed as

whereX(t)=(x1(t),x2(t),...,xn(t))is the state of all individuals at timet,the network topology structureA(t)at timetis defined in(5),FandGare the transfer functions for the dynamics of individual state and network topology,respectively.

The objective of this paper is to establish the matrix expressionoftheSISED-DN,basedonwhichweanalyze the epidemic spreading process and vaccination control problem.

3.2 Matrixexpressionforthedynamicsofindividual states

We first give the matrix expression of the dynamics of individual states via the STP approach.The dynamics of individual states we considered in this paper is presented as follows(see[3]for details).

Ateachtimeperiod,thesusceptiblebecomesinfected with the fixed probability threshold β,the infected individual recovers from the disease with probability threshold δ,becoming susceptible.That is to say,

where the healing function isfδ(x)=infected function isgβ(x)=state of individualiat timet,mi(t)the number of the infected neighbors for individuali,the parameters δi, βiis the immune probability and the infected probability of individuali,respectively,and 0 ＜ δi,βi＜ 1,i∈N.

To use matrix expression to SISED-DN,we express the individual state and the network into vector forms.

On one hand,for each individual state,by identifying theinfectedstateI∼andthesusceptiblestateS∼we have{S,I}∼ Δ2.

On the other hand,we consider how to express all the possible network topologieslogical variables.For any graph with its adjacent matrixAsatisfyingaij=ajiandaii=0,i,j∈N,it is easy to see thatAcan be determined uniquely byupper triangular components.Thus,we denote the network topology by(a12,...,a1n,...,ai,i+1,...,ai,n,...,an-1,n):=(b1,b2,...,bq),whereaij(t)=bα(ij)(t)with and

Now,we are ready to establish the matrix expression of the dynamics of individual states.First,we need to construct the structural matrix of transfer functionFfor the dynamics of individual states.Form equation(7),it is obvious that the state of each individual only depends on the states of his neighbors and the network topology structure in the previous period.Then,we have the following proposition.

Proposition 1The evolutionary dynamics of individual states can be expressed as

Considering the evolutionary rule(7)of individual states,one can see that the infected individual is only affected by the healing process,while the infected process only affects the susceptible.Thus,using the vector form of individual state,we have

wherexi(t)∈Δ2,i∈N.

Next,for the healing function,considering that

Moreover,the number of the infected neighbors for in-dividualiat timetcan be converted into

Then,the evolutionary dynamics of individual states can be converted into

whereLi=[MfδMgβ]W[2q+i-1,2](I2q+i-1⊗OR2) ∈ L2×2q+n,i∈N.Multiplying the above equations together yields

whereA(t)and Coli(LF)=Coli(L1)···Coli(Ln),i∈N.

Remark 1Equation(11)is the matrix expression of the dynamics of individual states(5),based on which we can analyze the epidemic spreading process.

3.3 Matrix expression for the dynamics of network topologies

Using the STP method,we establish the matrix expression for the dynamics of network topologies in this section.The network topology adjustment rule we consider here,which is referred to as preferential rewiring,is that for every SI link,the susceptible one with the highest priority breaks the link to the infected who have the lowest priority at each time,and forms a new link to the high-priority unconnected susceptible individual.For convenience,we order all the individuals by the priority degree,that is,d1＞d2＞...＞dn,wheredidenotes the priority degree of individuali.

For each possible network topologyA(t)=at timetand each state of individualsX(t+1)=at timet+1,we determine the network topology of the next period,1≤m≤2q,1≤l≤2n.

Define a set

which stands for the set of pairs of individuals with SI link.

If|Ql,m|=0,thenetworktopologyattimet+1remains unchanged,that is,A(t+1)=A(t).

If|Ql,m|=r≥1,then the network topology will be updatedunderthenetworkupdatingrule.Bythepriority degree,the individual who can adjust his neighbors isi＊,wherei＊=min{i|(i,j)∈Ql,m}.According to the network adjustmentrule,findtheinfectedneighborwiththelowestpriorityji＊=max{j|(i＊,j)∈Ql,m},andthesusceptible individual without linkˆji＊=min{j|Col(m-1)2n+l(Mi＊j)=It should be pointed out that the susceptible individual without link may not exist.In this case,no new link is formed for individuali＊.

It should be pointed out that when the link between individualsiandjbreaks,aij(t)changes fromandmα(ij)from 1 to 2.Likewise,when a link is created between two individualsiandj,aij(t)changes fromtoandmα(ij)from 2 to 1.

Correspondingly,when a new link(i,j)is created or an old link breaks in the network,the whole network topology changes to

It should be pointed out equation(12)is the matrix expression for the dynamics of network topologies(6).

4 Analysis and vaccination control for SIS epidemic dynamics over dynamic networks

4.1 Final spreading equilibria of SISED-DN

In this part,we analyze the final spreading equilibria of the SISED-DN.

Substituting(11)into(12)yields

Then,the matrix expression of SISED-DN can be ob-

In fact,all the properties of SISED-DN can be revealed from the matrix expression,equivalently,from the transition matrixL.Then,we can obtain all the final spreading equilibria according to the following result,where a equilibrium means both the individual state and the network topology be stationary,a cycle represents the individual state and the network topology change periodically.

Lemma 2[10] 1)The number of cycles of lengthsfor the epidemic dynamics(13),denoted byNs,is inductively determined byN1=tr(L)and

where P(s)denotes the set of proper factors ofs,the proper factor ofsis a positive integerk＜ssatisfyings/k∈Z+,and Z+is the set of positive integers.

2)The set of elements on cycles of lengths,denotedset of diagonal nonzero columns ofL.

Next,we use a very simple example to demonstrate our main results.

Example 1There are three small retailers,who have business relationship.Assume that some of them are infected by an epidemic disease.To avoid being infected,the other retailers adjust their business relationship to respond to the emergence of the epidemic.Our objective is to investigate the evolutionary process of the epidemics and obtain all the final spreading equilibria.

In fact,the situation can be modeled as the SISEDDN presented in Section3.1,whereN={1,2,3},the parameters δ =0.51,δ1=0.6,δ2=0.55,δ3=0.4 and β =0.5,β1=0.75,β2=0.4,β3=0.6.By the vector form of logical variables,we identify the individual stateSimilarly,identifyandaij=whereA=(aij)n×nis the adjacent matrix of a graph.

First,by the discussion of Sections3.1 and 3.2,one can convert the dynamics of individual states and network topologies into matrix expressions(11)and(12),respectively.With the help of MATLAB,a direct calculation shows the structural matricesLF=δ8[7 7 7 8 3 4 3 8 7 8 7 8 3 4 3 8 7 8 7 8 3 4 7 8 7 8 7 8 3 4 7 8 7 7 7 8 3 8 3 8 7 8 7 8 3 8 3 8 7 8 7 8 7 8 7 8 7 8 7 8 7 8 7 8]andLG=δ8[1 2 2 5 3 5 3 1 2 4 6 5 4 6 4 2 3 4 4 7 7 5 4 3 4 4 8 7 8 6 4 4 5 6 6 7 7 6 3 5 6 8 6 7 8 6 4 6 7 8 8 7 7 6 4 7 8 8 8 8 8 8 8 8].

It follows that the matrix expression of the SISED-DN is

whereX(t)=x1(t)x2(t)x3(t)is the individual states at timet,A(t)=a12(t)a13(t)a23(t)is the network topology at timet,and the structural matrix is

From Lemma 2,the set of all the final spreading equilibria iswhich implies that the final individual states are that all individuals become healthy except the two cases ofand(see Fig.2).

Fig.2 The two cases ofandThe white nodes are susceptible individuals and the black ones are infected individuals.

Next,we compare(14)with the epidemic dynamics without the rewriting of network topologies.Assume that the disease spread on a fixed fully connected network.From the matrix expression

Fig.3 The evolutionary trajectory of individual states starting from all possible X(0)∈ Δ8when the network is static and fully connected,where the y-coordinate Xi denote the initial individual statei=1,2,···,8.

Remark 2From the expression(13)and Lemma 2,all the final equilibria of the SISED-DN can be obtained.It should be pointed out that when the size of the network is not small,establishing the algebraic formulation directly is very difficult.In our future work,we will focus on how to reduce the computational complexity and find a more effective algorithm to study the SISED-DN.

4.2 Vaccination control of SISED-DN

From Example 1,one can see that though adaptive networks can obstruct the wide spread of infectious diseases to some extent,it may not ensure the disease self-healing(see Fig.4).In order to control infectious diseases more effectively,vaccination is a fundamental strategy adopted by the government and medical institutions,which can be perceived as an external control.

Fig.4 The evolutionary trajectory of individual states starting from all possible X(0)∈Δ8when the network is dynamic and the initial network is fully connected.

Assume that if an individual is vaccinated at timet,he/she will become susceptible at timet+1.Moreover,the effectiveness of vaccines can only maintain along a unit of time.Letui(t)be the control from the government,denoting whether to inject vaccine for individuali.Thus,by identifying the control strategy“not inject vaccine for the individual"∼,and “inject vaccine for the individual"∼,we have

Plugging(16)into(12),it follows that

This together with(16)implies

whereG∈ L2n×2n.

Theorem1ConsidertheSISED-DN(17)understate feedback vaccination control(18).The final evolutionary equilibrium is that all the individuals become susceptible for any initial individual state and network topology,if and only if there exists an integer τ such that

Proof(Sufficiency) By(17)and(18),we have

which implies thatA(τ)X(τ)=ˆLτA(0)X(0).It is noted that

Then,for any initial individual stateX(0)and network topologyA(0),one can obtain thatX(τ)=When every individual becomes susceptible,both the individual states and the networks will be stationary,unless a new epidemic outbreaks.Therefore,X(t)=t≥ τ,namely,the final evolutionary equilibrium is that all the individuals become susceptible.

(Necessity)We prove it by reduction to absurdity.Suppose that there exists no τ such that

Without loss of generality,for anyt,suppose thatThis is a contradiction.The proof is completed. □

Remark 3It is noted that the existing vaccination control results[2,4]are mainly based on experiments or computer simulation to verify the effectiveness of vaccination strategy.The advantage of our method is that a sufficient and necessary condition for the existence of vaccination control is obtained by the rigorous mathematical analysis.

Example 2Recall Example 1.From the parameters δi,i=1,2,3 and δ,the first and second individual have higherimmunityandcanhealthemselves.However,the third individual has lower immune capacity and need to be vaccinated when he/she is infected.Thus,we consider the following state feedback vaccination controlui(t)= δ2[1 1]xi(t),i=1,2,u3(t)= δ2[2 1]x3(t),that is,

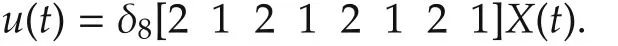
By Theorem 1 and with the help of MATLAB,one can obtain

satisfying the condition(19).As Fig.5 shows,this guarantees that the final evolutionary equilibrium is that the three retailers become healthy no matter what the initial individual state and network topology are.

Fig.5 The evolutionary trajectory of individual states starting fromallpossibleX(0)∈Δ8undervaccinationcontrolwhenthe network is dynamic and the initial network is fully connected.

5 Conclusions

In this paper,by using the STP approach,we have investigated epidemic dynamics over dynamic networks.Based on a formal SISED-DN and a class of determinate co-evolutionary rule,we have established the matrixexpressionsforthedynamicsofindividualstatesand network topologies,respectively.With the help of the matrix expression,all possible final spreading equilibria have been obtained for any given initial epidemic state and network topology.Moreover,a sufficient and necessary condition of the existence of state feedback vaccination control has been presented to ensure all people healthy finally.Illustrative examples have been given to support our new results.

[1]R.Pastor-Satorras,A.Vespignani.Epidemic spreading in scalefree networks.Physical Review Letters,2001,86(14):3200-3203.

[2]F.Fu,D.I.Rosenbloom,L.Wang,et al.Imitation dynamics of vaccination behaviour on social networks.Proceedings of the Royal Society B:Biological Sciences,2011,278(1702):42-49.

[3]Y.Song,G.Jiang,J.Xu.An epidemic spreading model in adaptive networks based on cellular automata.Acta Physica Sinica,2011,60(12):120509-1-120509-10.(in Chinese).

[4]M.Taylor,T.J.Taylor,I.Z.Kiss.Epidemic threshold and control in a dynamic network.Physical Review E,2012,85(1):DOI 10.1103/PhysRevE.85.016103.

[5]P.Holme,J.Saramaki.Temporalnetworks.PhysicsReports,2012,519(3):97-125.

[6]T.Gross,C.D’Lima,B.Blasius.Epidemic dynamics on an adaptive network.Physical Review Letters,2006,96(20):DOI 10.1103/PhysRevLett.96.208701.

[7]T.Gross,B.Blasius.Adaptive coevolutionary networks:A review.Journal of The Royal Society Interface,2008,5(20):259-271.

[8]L.B.Shaw,I.B.Schwartz.Fluctuating epidemics on adaptive networks.Physical Review E,2008,77(6):DOI 10.1103/PhysRevE.77.066101.

[9]V.Marceau,P.A.Noel,L.Hebert-Dufresne,et al.Adaptive networks:Coevolution of disease and topology.Physical Review E,2010,82(3):DOI 10.1103/PhysRevE.82.036116.

[10]D.Cheng,H.Qi,Z.Li.Analysis and Control of Boolean Networks:A Semi-tensor Product Approach.London:Springer,2010.

[11]D.Cheng,H.Qi.A linear representation of dynamics of Boolean networks.IEEE Transactions on Automatic Control,2010,55(10):2251-2258.

[12]F.Li,J.Sun.Controllability of Boolean control networks with time delays in states.Automatica,2011,47(3):603-607.

[13]H.Li,Y.Wang,Z.Liu.Stability analysis for switched Boolean networks under arbitrary switching signals.IEEE Transactions on Automatic Control,2014,59(7):1978-1982.

[14]Y.Zhao,Z.Li,D.Cheng.Optimal control of logical control networks.IEEE Transactions on Automatic Control,2011,56(8):1766-1776.

[15]Z.Liu,Y.Wang.Disturbance decoupling of mix-valued logical networksviathesemi-tensorproductmethod.Automatica,2012,48(8):1839-1844.

[16]Y.Wang,C.Zhang,Z.Liu.A matrix approach to graph maximum stable set and coloring problems with application to multi-agent systems.Automatica,2012,48(7):1227-1236.

[17]M.Xu,Y.Wang,A.Wei.Robust graph coloring based on the matrix semi-tensor product with application to examination timetabling.Control Theory and Technology,2014,12(2):187-197.

[18]X.Xu,Y.Hong.Matrix expression and reachability analysis of finite automata.Journal of Control Theory and Applications,2012,10(2):210-215.

[19]F.Song,S.Qin.A novel fault diagnosis method for satellite systems based on multivalue logic inference with semi-tensor product of matrices.Proceedings of the IEEE Conference on Prognostics and System Health Management,Beijing:IEEE,2012:1-5.

[20]H.Li,Y.Wang.Boolean derivative calculation with application to fault detection of combinational circuits via the semi-tensor product method.Automatica,2012,48(4):688-693.

[21]D.Cheng.On finite potential games.Automatica,2014,50(7):1793-1801.

[22]D.Cheng,Y.Zhao,Y.Mu.Strategy optimization with its application to dynamic games.Proceedings of the 49th IEEEConference on Decision and Control,Atlanta:IEEE,2010:5822-5827.

[23]D.Cheng,H.Qi,F.He,et al.Semi-tensor product approach to networked evolutionary games.Control Theory and Technology,2014,12(2):198-214.

[24]D.Cheng,T.Xu,H.Qi.Evolutionarilystablestrategyofnetworked evolutionary games.IEEE Transactions on Neural Networks and Learning Systems,2014,25(7):1335-1345.

[25]P.Guo,Y.Wang,H.Li.Algebraic formulation and strategy optimization for a class of evolutionary networked games via semi-tensor product method.Automatica,2013,49(11):3384-3389.

DOI10.1007/s11768-016-5101-2

†Corresponding author.

E-mail:guopeilian0127@163.com.

This work was supported by the National Natural Science Foundation of China(Nos.61374065,61503225),the Research Fund for the Taishan Scholar Project of Shandong Province,and the Natural Science Foundation of Shandong Province(No.ZR2015FQ003).

her B.Sc.degree and M.Sc.degreefromtheDepartmentofMathematics,Shandong Normal University,Jinan,China,in 2009 and 2012,respectively.Since 2012 she has been pursuing her Ph.D.degree at the School of Control Science and Engineering,Shandong University,Jinan,China.Her research interests include game theory andlogical dynamic systems.E-mail:guopeilian0127@163.com.

YuzhenWANGgraduatedfromTai’an Teachers College in 1986,received his M.Sc.degree from Shandong University of Science and Technology in 1995,and his Ph.D.degree from the Institute of Systems Science,Chinese Academy of Sciences in 2001.Since 2003,he is a professor with the School of Control Science and Engineering,Shandong University,China,and now the Dean of the School of Control Science and Engineering,Shandong University.From 2001 to 2003,he worked as a Postdoctoral Fellow in Tsinghua University,Beijing,China.From Mar.2004 to Jun.2004,from Feb.2006 to May 2006 and from Nov.2008 to Jan.2009,he visited City University of Hong Kong as a Research Fellow.From Sept.2004toMay2005,heworkedasavisitResearchFellowattheNational University of Singapore.His research interests include nonlinear control systems,Hamiltonian systems and Boolean networks.Prof.Wang received the Prize of Guan Zhaozhi in 2002,the Prize of Huawei from the Chinese Academy of Sciences in 2001,the Prize of Natural Science from Chinese Education Ministry in 2005,and the National Prize of NaturalScienceofChinain2008.Currently,heisanassociateeditorof IMA Journal of Mathematical Control and Information,and a Technical Committee member of IFAC(TC2.3).E-mail:yzwang@sdu.edu.cn.