Distributed non-cooperative robust MPC based on reduced-order models

Yushen LONG,Shuai LIU,Lihua XIE,Karl Henrik JOHANSSON

1.School of Electrical and Electronic Engineering,Nanyang Technological University,639798,Singapore;

2.ACCESS Linnaeus Center,School of Electrical Engineering,Royal Institute of Technology,SE-100 44,Stockholm,Sweden Received 1 December 2015;revised 20 December 2015;accepted 20 December 2015

Distributed non-cooperative robust MPC based on reduced-order models

Yushen LONG1†,Shuai LIU1,Lihua XIE1,Karl Henrik JOHANSSON2

1.School of Electrical and Electronic Engineering,Nanyang Technological University,639798,Singapore;

2.ACCESS Linnaeus Center,School of Electrical Engineering,Royal Institute of Technology,SE-100 44,Stockholm,Sweden Received 1 December 2015;revised 20 December 2015;accepted 20 December 2015

In this paper,a non-cooperative distributed MPC algorithm based on reduced order model is proposed to stabilize large-scale systems.The large-scale system consists of a group of interconnected subsystems.Each subsystem can be partitioned into two parts:measurable part,whose states can be directly measured by sensors,and the unmeasurable part.In the online computation phase,only the measurable dynamics of the corresponding subsystem and neighbour-to-neighbour communication are necessary for the local controller design.Satisfaction of the state constraints and the practical stability are guaranteed while the complexity of the optimization problem is reduced.Numerical examples are given to show the effectiveness of this algorithm.

Model predictive control,distributed control,building energy efficiency DOI10.1007/s11768-016-5125-7

1 Introduction

Due to its capability to handle hard constraints on state,control input and output explicitly,and optimize the performance of the system with respect to the cost function[1-3],model predictive control(MPC)has received increasing attention in the last decades.At each time instant,the controller is required to solve a finite horizon optimal control problem and the first element of the control sequence is applied to the plant.Then the optimization problem is reformulated when a new measurement comes and it is solved again.Traditionally,to compute the optimal control input,the controller needs the full model and state/output information of the system,and the optimization problem is formulated and solved in a centralized manner.However,when interconnected large scale systems such as power systems[4],traffic networks[5],biology systems[6]and building systems[7]are considered,it is usually not practical for the controller to know the full model and state/output information,and solve the optimization problem in reasonable time.To overcome these obstacles,distributed model predictive control(DMPC)is proposed in a lot of literatures[8-11].

Usually,in the DMPC setup,the model complexity mainly comes from the large number of interconnected subsystems.In some industrial control applications,eachsubsystemmayalsohavecomplexdynamics.For example,the model of heating,ventilation and airconditioning(HVAC)systems in buildings are usually obtained by discretization of partial differential equations[12,13].To guarantee high accuracy,the number of the grids should be large enough and the resulted ordinary differential equations usually have high dimension.Furthermore,because of the limited number of sensors,it is not practical to measure every state of a HVAC system.Therefore,even though the HVAC system in a building can be partitioned into connected subsystems by zones and rooms,the complexity of each subsystem should be reduced further.Model reduction techniques have been proposed in several literatures to simplify system dynamics at the expense of some modelling error[14,15].

In this paper,we consider a distributed control problem for a large-scale interconnected system where its subsystem also has complex dynamics.Based on the similar idea in[16],the dynamics of each subsystem is assumed to be partitioned to the main dynamics and the minor one.Only the states of the main dynamics are assumed to be measurable.Then for each subsystem,an MPC controller is designed only based on the main dynamics,by which the complexity of the controller is reduced.The modelling errors are handled as disturbances.Then it is shown that this problem can be cast into robust distributed MPC by using an algorithm proposed in[11].In[11]and[17],the authors studied the distributed algorithms and the implementation issues for large-scale linear systems.Compared with these two works,in this paper,we consider a more complex model and a model reduction technique is introduced to reduced the computational burden.

The remainder of this paper is organized as follows.In Section 2,the problem is formulated.In Section 3 and 4,the design and implementation procedures of the MPC controller are given.In Section 5,a numerical example is given to illustrate our algorithm.Finally,some conclusions are drawn in Section 6.

Some remarks on notations are given as follows.R and N are used to denote the real number set and the naturalnumberset,respectively.0denotesazeromatrix with proper dimension.Them×ndimensional space is denoted as Rm×n.A matrix is Schur stable if its eigenvalues lie in the interior of the unit circle.The Minkowski sum of setsAandBis defined asC=A⊕B={c=a+b,∀a∈Aandb∈B}.ThePontryagindifferenceofsetsAandBis defined asC=AөB={c|c+b∈A,∀b∈B}.For a discrete-time signalskanda,b∈N,a＜b,we denotes[a:b]as(sa,sa+1,...,sb).Given a generic compact set X,Y=box(X)is the smallest hyperrectangle containing X with faces perpendicular to the cartesian axis.

2 Problem formulation

Consider a linear discrete-time system

wherex(k)∈Rnis the state of the system,u(k)∈Rmis the control input andw(k)∈Rpis the external disturbance.

The system can be partitioned intoNlinear,discretetime,interconnected non-overlapping subsystems.For each subsystem Si,the system dynamics is given by

wherexi(k)∈Rni,ui(k)∈Rmiandwi(k)∈Rwiare the state,the control input and the bounded external disturbance for subsystemiandAccording to this decomposition,we havex(k)=(x1(k),...,xN(k)),u(k)=(u1(k),...,uN(k)),

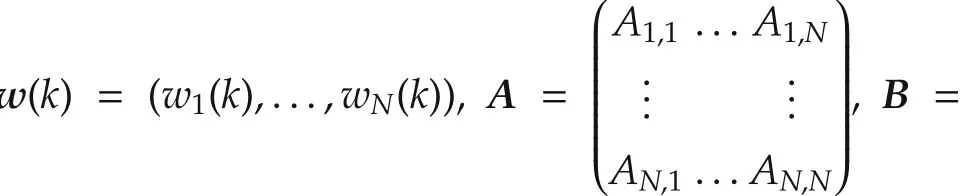
Eachxi(k)can be further partitioned into two parts:measurable partand unmeasurable partwheren1,i≪n2,i.The matricesAi,j,BiandDihave the corresponding structures:

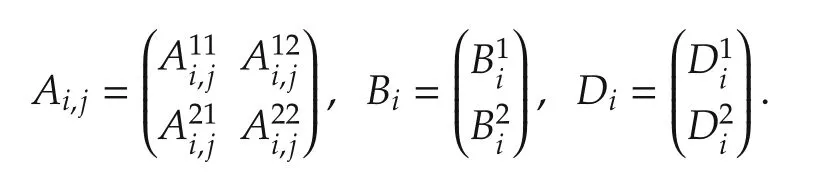
3 Controller design

For simplicity,in this section,we assume thatandare 0,∀i≠ j.

3.1 Bounded unmeasurable state

First we rewrite the dynamics ofinto the following form:

Thus we obtain

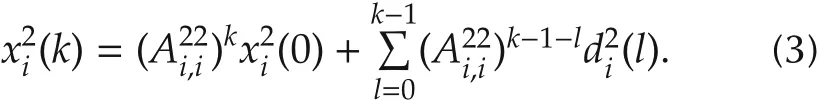
Considering the bounds on xi(k),xj(k)and ui(k),we know thatTherefore by(3),we haveAn over-approximationcanbeeasilygivenbyRewrite the dynamics ofin the following form:

From the above discussion,we know thatThis fact implies that can be treated as an additive bounded disturbance to

Therefore,distributed robust MPC can be designed to stabilize this system.

3.2 Distributed robust MPC

Consider the nominal subsystem model

Before providing the distributed robust MPC algorithm,the following assumption on decentralized stabilizability is necessary.

Assumption 1There exist matrices Ki,i=1,...,N such that i)Schur,whereand K=diag{K1,...,KN}.

The control law for the ith subsystem(2)is given by

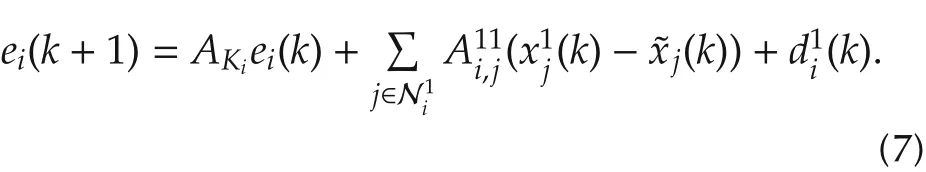
Due to the stability of the matrix AKiand the boundedness of di(k),if it can be further guaranteed that(k)-(k)are bounded,∀j=1,...,N,there exists a robust positively invariant setfor(7),such thatwhich implies that if

At each time instant t,each subsystemtransmits its future state and control reference trajectory over the prediction horizonto its neighbors,and the MPC controller of each subsystemsolves the following ith optimization problem:

and fork=t,...,t+Nc-1 andl=1,...,nc,

Remark 1(8)implies thatei(t)∈.Based on the invariance ofand by induction,it follows thatei(k)∈,k=t,...,t+-1.Combining this fact with constraint(10),it can be obtained that∑ which guarantees the boundedness of.Considering(7),a sufficient condition of the setsandis that

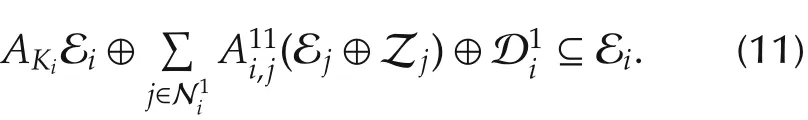
The following assumptions for the terminal constraintand terminal cost function(·)are necessary to guarantee the recursive feasibility of the optimization problem and stability of the system.

Assumption 2Denote

At each time instantt,a paircan be obtained by Siby solving theith problem.Based on(5)and(6),the future state trajectorycan also be computed.Then setandas the last elements of the reference state and control trajectory and transmitted to the neighbours of theith subsystem for updating and reformulating the local optimization problems at time instantt+1.

Based on the above setup,we have the following convergence result of the distributed MPC algorithm.

Theorem 1If Assumptions 1 and 2 hold,thenexponentially converges to the invariant set of systemx(k+1)=where

The proof goes along the line of Theorem 1 in[11]so it is omitted here.

4 Implementation

In this section,some algorithms for the computation of the weighted matrices,the feedback gains,the invariant sets and the initial feasible reference trajectory will be briefly introduced[17].

4.1 Feedback gains and weighted matrices

DenoteR=diag{R1,...,RN}.Define matricesS=R-1andY=KS.ConsideringSandYas feasible solutions to the following LMI,the feedback gainKiand terminal weighted matricesRiwhich satisfy Assumption1 withcan be obtained by the definition ofSandY.

whereSi,jandYi,j,∀i,j=1,...,Nare the(i,j)th block ofSandY.

OnceKandRare computed,P=diag{P1,...,PN}andQ=diag{Q1,...,QN}can be constructed to satisfy Assumption 2 iii)by considering the following inequality:

4.2 Computation of sets

Algorithm 1

Step 1Initialize Zi,i=1,...,N as arbitrarily hyperrectangles.

Step 2Initialize

Step 3Compute

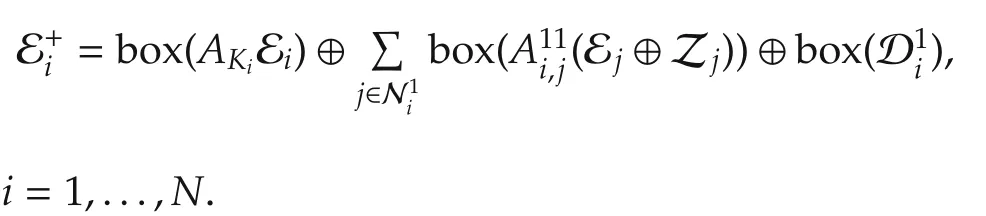
Step 4For all i=1,...,N,ifwhich means thatisatisfies(11),then go to Step 5.Otherwise setand repeat Step 3.

Step 5then stop.Otherwise setand go to Step 2.

4.3 Initial feasible reference trajectories

Denote the current measurement of system state isThe algorithm to find the initial feasible reference trajectories of each subsystem Siis based on the one-step prediction.

Algorithm 2

Step 1For all i=1,...,N,initialize

Step 2For all i=1,...,N,each subsystem Sitransmitsitsstatetoitsneighboursandsolves the following optimization problem.

Step 3For i=1,...,N,set prediction horizon as v+1 and stop.Otherwise,set v=v+1 and go to Step 2.

5 Numerical example

In this section,the proposed control algorithm is tested on a building temperature regulation problem proposed in[17]with slightly modification.

Consider four connected rooms A,B,C and D as in Fig.1.Rooms A and B are combined together as one apartment while rooms C and D as the other apartment.TheairtemperatureTA,TB,TCandTDareconsideredas the measurable states and the control objective is to regulate them to the set point.Each room is equipped with anair-conditionerqA,qB,qCandqD.TheheattransfercoefficientbetweenroomsA-CandB-Disthe one between rooms A-B and C-D isand the one between each room and the external environment isThe nominal external temperatureis 35◦C and solar radiation is not considered for simplicity.The volume of each room is V=48m3,and the wall surfaces between the rooms are all equal to sr=12m2,while those between the rooms and the environment are equal to se=24m2.Air density and heat capacity are ρ=1.225kg/m3and c=1005J/kgK,respectively.Letting φ = ρcV,the dynamic model is as follows:

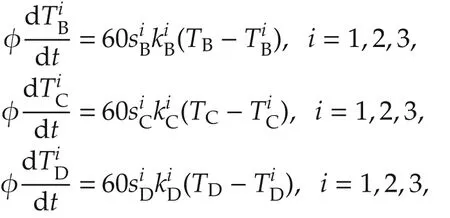
where,i=1,2,3 are used to represent the thermal dynamics of furniture and walls which are assumed unmeasurable,are the equivalent surfaces chosen randomly,andandare the equivalent heat transfer coefficients chosen randomly.

Fig.1 Schematic representation of a building with two apartments.

The considered equilibrium point is:?

The corresponding discrete-time model of the form(1)is obtained by mE-ZOH discretization[18]with sampling time h=10s.The partition of inputs and measurable states is:

The constraints on the inputs and the states of the discretized system is

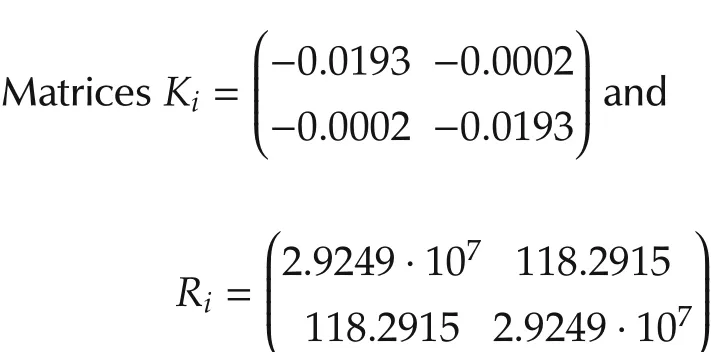
areconstructedbyfindingfeasiblesolutionstoLMI(12)-(15).The selected weighting matrices arePi=I2andQi=100I2.Algorithm 1 is used to find the invariant sets andtheinitialfeasiblereferencetrajectoryisconstructed by using Algorithm 2 withNc=6.

The initial condition of this numerical example is δTA=3◦C, δTB=2◦C, δTC=4◦C and δTD=5◦C.The initial temperature of the unmeasurable states are randomly chosen between[22◦C,25◦C].The real external temperature is assumed to randomly vary between[25◦C,45◦C].At time instantt=700s,there is a sudden increase of temperatureTAandTBrepresenting the opening of doors and windows.Over time interval[700s,1400s]additional heat sources with 30◦C are added in both rooms.The control input is calculated by using the descretized model and applied to the continuous-time model.The simulation results are shown in Fig.2.

Fig.2 State and input trajectory of distributed algorithm.

To compare the performance of the proposed distributed algorithm,a decentralized MPC and a centralized MPC with complete state information are also used to regulate the temperature.The simulation results are shown in Figs.3 and 4.

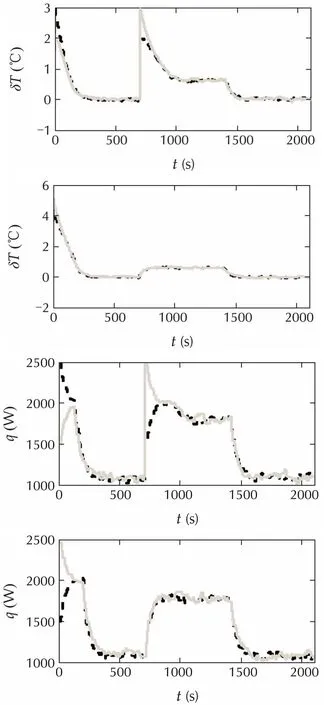
Fig.3 State and input trajectory of decentralized algorithm.

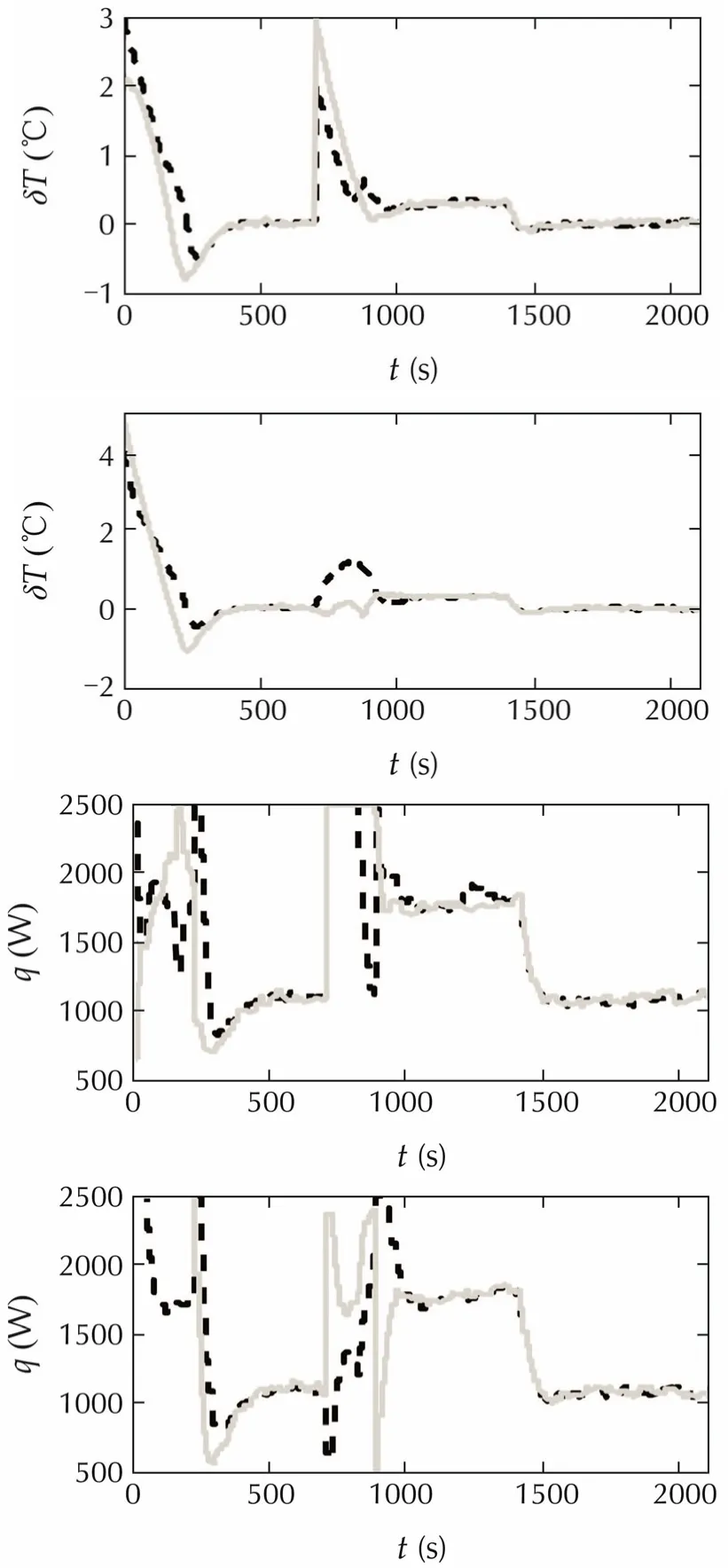
Fig.4 State and input trajectory of centralized full order algorithm.

To show the difference among these algorithms more clearly,the temperature deviation between distributed algorithm and the decentralized algorithm are shown in Figs.5 and 6.The temperature deviation between distributed algorithm and the centralized algorithm are shown in Figs.7 and 8.

In Figs.2-4,the black dashed lines represent the corresponding main states and control inputs of rooms A and C while the grey solid lines represent those of rooms C and D.In Fig.5 the black dashed line represents δTA,dis- δTA,decand the grey solid line represents δTB,dis- δTB,dec,and in Fig.6 they represent δTC,dis- δTC,decand δTD,dis- δTD,dec,respectively.In Fig.7theblackdashedlinerepresentsδTA,dis-δTA,cand the grey solid line represents δTB,dis-δTB,c,and in Fig.8 they represent δTC,dis-δTC,cand δTD,dis-δTD,c,respectively.The subscripts dis,dec,c represent distributed algorithm,decentralized algorithm and centralized algorithm,respectively.For clarity reason,the minor dynamics are not shown in these figures.

In the decentralized algorithm,there is no information exchange between controllers.Therefore,the joint constraint ‖u1‖1+ ‖u2‖1≤ 8000 is tightened as‖u1‖1≤ 4000 and ‖u2‖1≤ 4000.The dynamics coupling terms are treated as unknown bounded disturbance and the method in[19]are used to design local controller.For the centralized algorithm,we also follow the way in[19]to design the centralized controller.

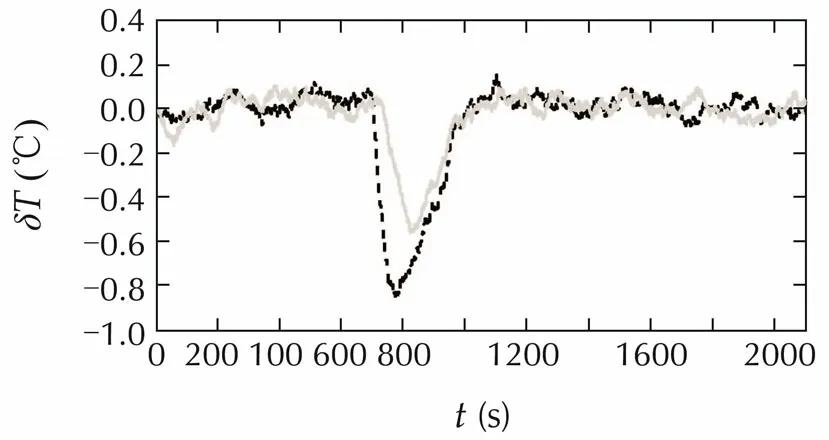
Fig.5 Temperature deviation between distributed and decentralized algorithm(rooms A and B).In this example,the air-conditioning system is working on cooling mode.Therefore,the distributed algorithm has faster response than the decentralized one since the former one has lower temperature.

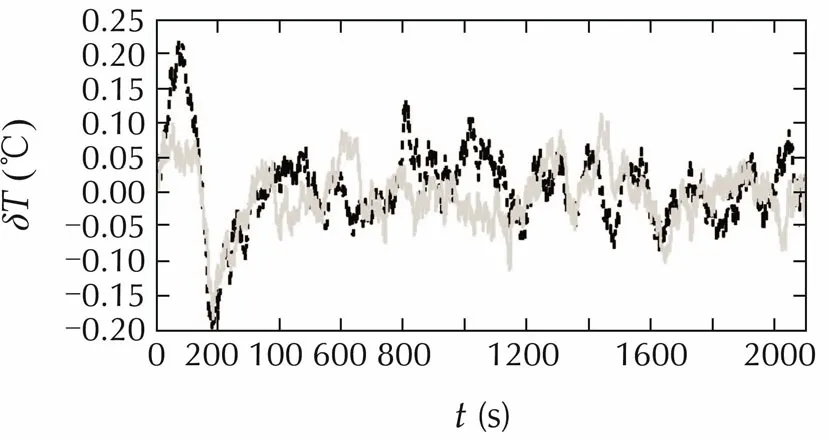
Fig.6 Temperature deviation between distributed and decentralized algorithm(rooms C and D).

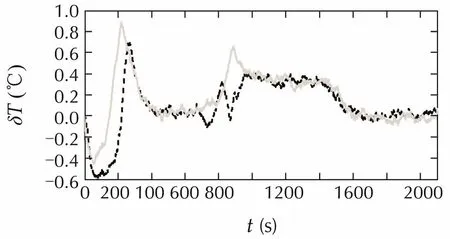
Fig.7 Temperature deviation between distributed and centralized algorithm(rooms A and B).

Fig.8 Temperature deviation between distributed and centralized algorithm(rooms C and D).

From Figs.2-4 it can be observed that with the additional heat source,all the three algorithms have some off-set.FromFigs.5and6onecanseethatdistributedalgorithm has faster response than the decentralized one.This is due to the fact that in the distributed algorithm,controllers can communicate with each other.Therefore,controllers for rooms A and B know how much power will be used by the other two controllers and the overall power,which is restricted to be less or equal to 8000W,can be used more efficiently.This fact can also be observed in Figs.2 and 3.In Fig.2,controllers for rooms A and B attain the maximal power 2500W while in Fig.3,their power has to satisfy the constraintqA+qB≤4000W.The off-set of both algorithms are similar.Figs.7 and 8 show that centralized algorithm has faster response than the distributed one and its offset is also smaller than that of the distributed one.This is not surprising because the centralized algorithm utilizes the complete state information.

Finally,we compare the energy,which is defined as and the average computational time consumed by the three algorithms in Table 1.

Table 1 Cost and average computational time of the three algorithms.

6 Conclusions

In this paper,a distributed robust MPC algorithm has been proposed.Each subsystem can be partitioned into measurable main dynamics and unmeasurable minor dynamics.Only the main dynamics is used to predict the future trajectory while the minor dynamics is not handled explicitly in the online computation,by which the complexity of the optimization problem is significantly reduced.Numerical examples has been given to illustrate the effectiveness of our algorithm.

[1]D.Q.Mayne,J.B.Rawlings,C.V.Rao,et al.Constrained model predictive control:Stability and optimality.Automatica,2000,36(6):789-814.

[2]J.B.Rawlings.Tutorial overview of model predictive control.IEEE Control Systems,2000,20(3):38-52.

[3]S.Qin,T.Badgwell.A survey of industrial model predictive control technology.Control Engineering Practice,2003,11(7):733-764.

[4]P.Cortes,M.P.Kazmierkowski,R.M.Kennel,et al.Predictive control in power electronics and drives.IEEE Transactions on Industrial Electronics,2008,55(12):4312-4324.

[5]T.Tettamanti,I.Varga,B.Kulcsar,et al.Model predictive control in urban traffic network management.Mediterranean Conference on Control and Automation,New York:IEEE,2008:1538-1543.

[6]R.Hovorka,V.Canonico,L.J.Chassin,et al.Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes.Physiological Measurement,2004,25(4):905-920.

[7]Y.Ma,G.Anderson,F.Borrelli.A distributedpredictivecontrol approach to building temperature regulation.Proceedings of the American Control Conference,New York:IEEE,2011:2089-2094.

[8]A.Venkat,J.Rawlings,S.Wright.Stability and optimality of distributedmodelpredictivecontrol.IEEEConferenceonDecision and Control and European Control Conference,New York:IEEE,2005:6680-6685.

[9]W.B.Dunbar.Distributed receding horizon controlof dynamically coupled nonlinear systems.IEEE Transactions on Automatic Control,2007,52(7):1249-1263.

[10]J.Liu,X.Chen,D.Muoz de la Pea,et al.Sequential and iterative architecturesfordistributedmodelpredictivecontrolofnonlinear process systems.AIChE Journal,2010,56(8):2137-2149.

[11]M.Farina,R.Scattolini.Distributed predictive control:A noncooperative algorithm with neighbor-to-neighbor communication for linear systems.Automatica,2012,48(6):1088-1096.

[12]T.Kim,S.Kato,S.Murakami.Indoorcooling/heatingloadanalysis based on coupled simulation of convection,radiation and hvac control.Building and Environment,2001,36(7):901-908.

[13]F.Moukalled,S.Verma,M.Darwish.The use of cfd for predicting and optimizing the performance of air conditioning equipment.International Journal of Heat and Mass Transfer,2011,54(13):549-563.

[14]S.Goyal,P.Barooah.A method for model-reduction of non-linear thermal dynamics of multi-zone buildings.Energy and Buildings,2012,47:332-340.

[15]K.Deng,S.Goyal,P.Barooah,et al.Structure-preserving model reduction of nonlinear building thermal models.Automatica,2014,50(4):1188-1195.

[16]P.Sopasakis,D.Bernardini,A.Bemporad.Constrained model predictive controlbased on reduced-ordermodels.IEEEConferenceonDecisionandControl,NewYork:IEEE,2013:7071-7076.

[17]G.Betti,M.Farina,R.Scattolini.Realization issues,tuning,and testing of a distributed predictive control algorithm.Journal of Process Control,2014,24(4):424-434.

[18]M.Farina,P.Colaneri,R.Scattolini.Block-wise discretization accounting for structural constraints.Automatica,2013,49(11):3411-3417.

[19]D.Q.Mayne,M.M.Seron,S.V.Rakovi.Robust model predictive controlofconstrainedlinearsystemswithboundeddisturbances.Automatica,2005,41(2):219-224.

†Corresponding author.

E-mail:ylong002@e.ntu.edu.sg.Tel.:(+65)9811 3904.

This work was supported by the Republic of Singapore’s National Research Foundation through a grant to the Berkeley Education Alliance for Research in Singapore(BEARS)for the Singapore-Berkeley Building Efficiency and Sustainability in the Tropics(SinBerBEST)Program.BEARS has been established by the University of California,Berkeley as a center for intellectual excellence in research and education in Singapore.This work was also supported by the National Natural Science Foundation of China(Nos.61573220,61304045).

the B.Sc.degree in ControlEngineeringfromTianjinUniversity,China,in 2012.Currently,he is pursuing his Ph.D.degree of Control Engineering at Nanyang Technological University.His research interests are multi-agent systems,model predictive control,and building systems.E-mail:ylong002@e.ntu.edu.sg.

Shuai LIUreceived his B.E.and M.E.degrees in Control Theory and Engineering from Shandong University in 2004 and 2007,respectively,and his Ph.D.degree in Electrical and Electronic Engineering from Nanyang Technological University,Singapore,in 2012.Since 2011,he has been a research fellow with Berkeley education alliance for research in Singapore(BEARS).His research interests include cooperative control,distributed consensus,optimal estimation and control,time-delay systems,fault detection and estimation.E-mail:lius0025@e.ntu.edu.sg.

Lihua XIEreceived the B.E.and M.E.degrees in Electrical Engineering from Nanjing University of Science and Technology in 1983 and 1986,respectively,and the Ph.D.degree in Electrical Engineering from the University of Newcastle,Australia,in 1992.Since 1992,he has been with the School of Electrical and Electronic Engineering,Nanyang Technological University,Singapore,where he is currently a professor and served as the Head of Division of Control and Instrumentation from July 2011 to June 2014.He held teaching appointments in the Department of Automatic Control,NanjingUniversity ofScienceandTechnology from1986 to1989.Dr Xie’s research interests include robust control and estimation,networked control systems,multi-agent networks,and unmanned systems.He has served as an Editor-in-Chief of Unmanned Systems,an editor of IET Book Series in Control and an Associate Editor of a number of journals including IEEE Transactions on Automatic Control,Automatica,IEEE Transactions on Control Systems Technology,and IEEE Transactions on Circuits and Systems II.Dr Xie is a Fellow of IEEE and Fellow of IFAC.E-mail:elhxie@e.ntu.edu.sg.

Karl Henrik JOHANSSONis Director of the ACCESS Linnaeus Centre and Professor at the School of Electrical Engineering,KTH Royal Institute of Technology,Sweden.He is a Wallenberg Scholar and has held a Senior Researcher Position with the Swedish Research Council.He also heads the Stockholm Strategic Research Area ICT The Next Generation.He received M.Sc.and Ph.D.degrees in Electrical Engineering from Lund University.He has held visiting positions at UC Berkeley,California Institute of Technology,Nanyang Technological University,and Institute of Advanced Studies,Hong Kong University of Science and Technology.His research interests are in networked control systems,cyber-physical systems,and applications in transportation,energy,and automation systems.He has been a member of the IEEE Control Systems Society Board of Governors and the Chair of the IFAC Technical Committee on Networked Systems.He has been on the Editorial Boards of several journals,including Automatica,IEEE Transactions on Automatic Control,and IET ControlTheoryandApplications.HeiscurrentlyaSeniorEditorofIEEE Transactions on Control of Network Systems and Associate Editor of European Journal of Control.He has been Guest Editor for a special issue of IEEE Transactions on Automatic Control on cyber-physical systems and one of IEEE Control Systems Magazine on cyber-physical security.He was the General Chair of the ACM/IEEE Cyber-Physical Systems Week 2010 in Stockholm and IPC Chair of many conferences.He has served on the Executive Committees of several European research projects in the area of networked embedded systems.He received the Best Paper Award of the IEEE International Conference on Mobile Ad-hoc and Sensor Systems in 2009 and the Best Theory Paper Award of the World Congress on Intelligent Control and Automation in 2014.In 2009 he was awarded Wallenberg Scholar,as one of the first ten scholars from all sciences,by the Knut and Alice WallenbergFoundation.HewasawardedFutureResearchLeaderfrom the Swedish Foundation for Strategic Research in 2005.He received the triennial Young Author Prize from IFAC in 1996 and the Peccei Award from the International Institute of System Analysis,Austria,in 1993.He received Young Researcher Awards from Scania in 1996 and from Ericsson in 1998 and 1999.He is a Fellow of the IEEE.E-mail:kallej@ee.kth.se.