退化钢筋混凝土结构的时变可靠度分析

夏正兵

(江苏城市职业学院 建筑工程学院，江苏 南通 226006)



退化钢筋混凝土结构的时变可靠度分析

夏正兵

(江苏城市职业学院 建筑工程学院，江苏 南通 226006)

结构的耐久性退化是一个随机性很强的过程，退化结构的检修问题都涉及时变结构可靠度的计算。本文介绍了退化钢筋混凝土结构的抗力衰减模型及相关不确定性统计参数，分析了钢筋混凝土结构锈蚀受弯构件的抗力衰减规律。最后运用时间综合分析法计算了钢筋混凝土受弯构件锈蚀的时变可靠度。

结构耐久性; 钢筋混凝土; 退化

在众多的结构形式中，钢筋混凝土结构充分结合了钢筋和混凝土两种建筑材料的特性，造价低廉，因此在我们国家的基础建设过程中得到了大量推广[1]。长久以来，土木工程学科的学者们都在致力于寻求新材料的应用和结构体系的创新，在结构抗灾分析和设计理论上寻求突破[2]。然而，结构的耐久性和全寿命性能退化也是土木工程工作者关心的重要问题。

近年来，国内外大量学者根据影响结构耐久性的各种因素进行了大量的实验和观测，得到了许多针对混凝土结构耐久性的性能退化模型[3]。但这些模型是不能随着时间变化而变化的，这个缺点导致用时不变模型计算结构的可靠度将无法考虑结构的退化性能，本文则考虑了结构抗力和荷载随时间变化的特点，运用时变思想对可靠度进行计算。另外在阅读文献的过程中，我们发现，大多数学者研究的重点都在退化模型的构建上，对退化参数的专门研究很少。实际上，退化参数是退化模型的重要组成部分，基于正确的参数，结构的耐久性退化模型及后续的时变可靠度分析才有意义。本文的另一创新点就是在详细介绍退化模型的基础上，提出了钢筋混凝土相应的结构抗力不确定性统计参数，并从钢筋混凝土受弯构件入手，对钢筋混凝土锈蚀受弯构件的抗力衰减规律及时变可靠度进行分析。

1 结构可靠度分析方法的发展现状

目前，国内外对于时不变可靠度理论研究已相对成熟，而时变可靠度理论由于考虑因素更多，计算更为复杂，有待进一步深入研究。为此，诸多学者针对钢筋混凝土结构的时变可靠度展开了一系列的研究。2008 年，Czarnecki 等[4]发现处于腐蚀性环境条件下的钢筋混凝土结构抗力随时间变化显著，提出了一个关于钢筋混凝土结构的时变可靠度模型，并用此模型对结构的使用寿命进行了预测。2012 年，Frangopol[5]通过合并结构的先验知识与运用贝叶斯更新概念后所获得结构健康监测信息，对结构的退化性能作出了量化分析。2014 年，Madsen[6]提出了一种新的结构时变可靠度及灵敏度分析方法。同样地，国内的众多学者也在为推动结构时变可靠度分析的发展而在积极探索着。程寿山等[7]通过对钢筋锈蚀引起的结构抗力衰减过程进行分析，建立了结构将来状态的可靠性评估及预测方法。

2 钢筋混凝土抗力的退化模型的参数确定

2.1 抗力的参数确定

材料性能的不确定性主要是指耐久性退化引起的各种变异性，如混凝土碳化、钢筋锈蚀导致截面损失、混凝土保护层锈胀开裂脱落以及锈蚀钢筋力学性能退化等。

考虑计算模式不确定性，钢筋混凝土结构的抗力可以由以下公式表示：

P(t)=KrPr(t)

(1)

式中，P(t)——抗力随机过程； Kr——计算模式不确定性随机变量。

ωPr(t) = P[ωf aj(t),ωdj(t),ωKsj(t)]

(2)

(3)

(4)

该式中，Zj——影响抗力的相关随机变量

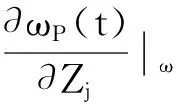
从上面的推导过程可以看出，要想得到最终抗力的统计特征，可以先确定抗力所包含的一些基本参数的统计特征。因为凭借目前的试验手段和研究条件，我们相对比较容易获得一些参数的统计特征，然后通过数学方法，便可以获得最终模型的不确定性统计规律，从而解决无法直接统计的难题。

2.2 锈蚀受弯构件抗力的统计参数

受弯构件是服役钢筋混凝土结构中最为常用的结构构件，经过对结构锈蚀构件多年的研究，锈蚀受弯构件的承载力计算已相对较为成熟。由混凝土相关知识可知，钢筋混凝土结构锈蚀构件矩形截面正截面受弯承载力可以由下式求得：

(5)

(6)

其中，Y——结构的正截面承载力大小(k N·m)； fv,fo——轴心抗压强度(MPa)； α1——系数，其取值按《混凝土结构设计规范》相关规定； l,b ——截面宽度，截面有效高度(mm)； Bse——受拉钢筋等效截面面积(mm2)。

根据以上分析，容易知道，通过对模型进行参数分析，从模型参数的不确定性出发，我们便可以最终求得钢筋混凝土结构锈蚀受弯构件抗力的相关不确定性统计参数。

3 结构时变可靠度分析方法

3.1 时间综合分析方法基本原理

时间综合分析方法就是在对结构进行可靠度分析的时候，把结构的整个服役期整体取为一个参考时间段，在这个时间段内考虑结构抗力与荷载的变化并得到我们需要的抗力及荷载模型。

在时间综合分析方法中，我们把结构的整个服役期看作一个参考时间段，与抗力及荷载相关的随机变量的统计特征全部是以这个参考时间段来考虑。结构在整个参考时间段内， P(t)和S(t)的实际情况如图 1所示：

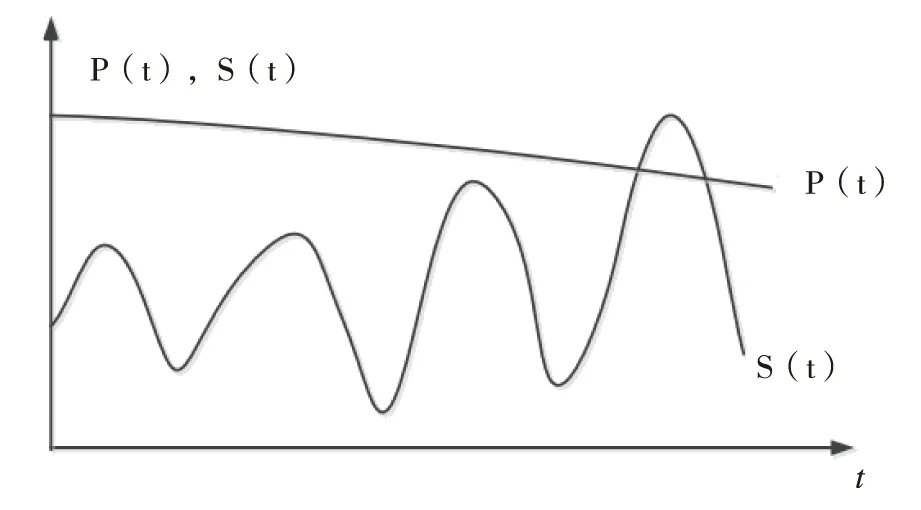
图1 结构抗力和荷载变化示意图Fig.1 Schematic structural resistance and load changes

从时变可靠度的概念上来说， P是一个定值，一般取参考时间段的最小值。需要说明的是，这里所说的定值并不是指确定的值，而是指的随机变量。我们可以由概率密度函数fp得到 P的实际值。

时间综合分析法中的失效概率，可以由下式求得：

(7)

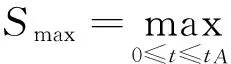
时间综合分析方法在实际应用的过程中，S(t)的概率密度函数可以通过一些长期的观测数据得到，这样，Smax便可以用概率分布函数求得。然而遗憾的是，大多数情况下，长期的观测数据很难得到，所以它的极值分布也可以用一些短期的数据来刻画。分析完结构构件相应的荷载与抗力变化规律，时变可靠度便可以用一次可靠度方法来计算。

3.2 锈蚀受弯构件时变可靠度分析

某地一钢筋混凝土受弯简支梁构件。其他相关抗力统计参数为ωKr=1.0，σKr=0.04；ωl=1.0l，σl=0.02；ωb=1.0b， σb=0.03；

简支梁承受承受恒载与活荷载 。恒载的平均值与标准差为ωG=28.91 k N/m，βG=2.02 k N/m。活荷载的平均值与标准差为 ωQ=0.585 k N/m，βQ=0.26 k N/m。

抗力平均值与变异系数经时变化曲线，见图2，图3。

图2 结构抗力平均值与使用年限变化曲线Fig.2 Structural resistance and service life of the average curve

图3 结构抗力变异系数与使用年限变化曲线Fig.3 Structual resistance and coefficient of variation life curve

4 小结

混凝土结构的耐久性的预测可行性研究现实意义重大，但要想取得精准的预测结果，至今还没有比较先进的方法。

本文经过计算得出相关计算参数，首先得出不确定性统计参数，在此基础上，计算了钢筋混凝土的锈蚀受弯构件的时变可靠度，总结得出锈蚀受弯构件可靠指标随结构服役期的变化规律。

该方法为混凝土结构的耐久性预测的新思考,该研究结论必将对现役混凝土结构的耐久性预测与安全性评估提供参考。因钢筋混凝土结构相关耐久性退化是一个非常复杂的过程，有些退化机理的研究至今仍然没有突破，本文对钢筋混凝土结构进行的耐久性退化分析只是考虑了很少的一部分，还存在许多问题有待解决。

[1]Li J，Gao X. Probability Density Evolution Method and its Application in Life-cycle Civil Engineering[J]. Structure and Infrastructure Engineering，2014，10(7)：921-927.

[2]Madsen H O， Tvedt L. Methods for Time-Dependent Reliability and Sensitivity Analysis[J]. American Society of Civil Engineers，2014，116(10)：2118-2135.

[3]Biondini F，Frangopol D M.Lifetime Reliability-based Optimization of Reinforced Concrete Cross-sections under Corrosion[J]. Structural Safety，2009，31(6)：483-489.

[4]Czarnecki A A，Nowak A S. Time-variant Reliability Profiles for Steel Girder Bridges[J]. Structural Safety，2008，30(1)：49-64.

[5]Okasha N M，Frangopol D M. Integration of Structural Health Monitoring in a System Performance based Life-cycle Bridge Management Framework[J]. Structure and Infrastructure Engineering，2012，8(11)：999-1016.

[6]Madsen H O，Tvedt L. Methods for Time-Dependent Reliability and Sensitivity Analysis[J]. American Society of Civil Engineers，2014，116(10)：2118-2135.

[7]程寿山，张劲泉，李万恒.钢筋锈蚀引起桥梁结构性能退化的可靠性分析[J].公路交通科技，2006，23(4):33-36.

Analysis of time-dependent reliability of degenerated reinforced concrete structure

XIA Zheng-bing

(College of Architecture and Civil Engineering, Jiangsu City Vocational College Nantong Campus, Nantong ,226006，China )

Material deterioration and structural damage are inevitable under the effects of man-made environment and natural environment during long-term use of structures. The accumulation of damages can directly result in degeneration of structural performance and gradually weaken the resistance of structure. Therefore, it is of great significance to predict the durability of reinforced concrete structure. This study emphatically introduced reinforced concrete structure resistance decrease model and related statistical parameters of uncertainty, analyzed resistance decrease rules of corroded bending element of reinforced concrete structure, and finally calculated time-dependent reliability of the corroded bending element of reinforced concrete structure, aiming to provide a specific theoretical basis for the application of time-dependent reliability theory.

Durability of structure; reinforced concrete;degeneration

2016-08-02

江苏省九三学社科技创新项目基金(项目编号：YHK1408);江苏省江豪专项资助项目基金(项目编号：1503)。

夏正兵(1982-)，男，江苏建湖人，江苏城市职业学院(南通)建筑工程学院讲师，江苏省九三学社工程建设支社社员、硕士。主要研究方向：建筑设备与混凝土材料。

TU528

A

1673-6125(2016)03-0044-03