图像拓扑意义下KKM点集的通有稳定性

杨彦龙，陈治友

(1.贵州大学 计算机科学与技术学院,贵州 贵阳 550025；2.贵阳学院 数学与信息科学学院, 贵州 贵阳 550005)



图像拓扑意义下KKM点集的通有稳定性

杨彦龙1，陈治友2

(1.贵州大学 计算机科学与技术学院,贵州 贵阳 550025；2.贵阳学院 数学与信息科学学院, 贵州 贵阳 550005)

为了获得在图像拓扑意义下上半连续KKM映射的KKM点集的通有稳定性，即在Baire分类意义下，绝大多数KKM映象的KKM点都是本质的。通过构造上半连续KKM映射G所组成的集合M, 并定义M上的KKM映射的图像之间的Hausdorff度量,证明了M是完备度量空间。然后利用usco方法,在证明了M上的KKM点集映射F是紧值上半连续的,从而由Fort定理得到F在M上是通有连续的, 即F是通有稳定的。

图像拓扑；通有稳定性；本质KKM点；剩余集；上半连续

0 引 言

1929年波兰数学家Kanaster, Kuratowski和Mazurkiewicz首次证明了KKM定理[1], 并由此形成的KKM技巧以及各种形式的理论推广[2-6], 特别是Ky Fan将该定理推广至无限维空间后[7], KKM技巧及理论在非线性分析中得到了更加广泛的应用。比如变分问题、最佳逼近问题、均衡问题等都可以转化为KKM问题。另一方面, 许多非线性问题的解并不唯一, KKM问题的解也是如此,例如Nash平衡问题解的不唯一性, 使得博弈论专家们不得不考虑解的“精炼”问题, 也就是如何寻找稳定的解。在现实问题中, 收集信息、构造模型及计算求解等过程中, 不可避免地出现与实际问题有出入的“扰动”。基于以上原因, 在[8-13]等工作的基础上, 特别是Yu和Xiang在[9]中考虑KKM映射的扰动, 本文利用图像拓扑, 证明了在Baire分类意义下, 绝大多数KKM映射都是本质的。下面先给出必要的预备知识,然后考虑上半连续KKM映射的图像扰动, 即在图像拓扑意义下, 利用usco方法, 证明上半连续KKM映射的KKM点集的通有稳定性。

1 预备知识

设X为Banach空间，记CL(X)表示X所有非空闭集的全体, K(X)表示X所有非空紧子集的全体。CL(X)和K(X)上的拓扑由Hausdorff度量产生。

引理1[14]设(X,d)为度量空间，则

(1) (CL(X),Hd)完备当且仅当(X,d)完备；

(2) (K(X),Hd)在(CL(X),Hd)中闭。

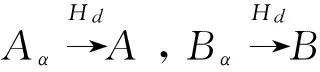
设(X,d)和(Y,ρ)是两个度量空间，2Y表示Y中所有非空子集。F:X→2Y是一个集值映射。

定义1 (1)如果对于Y中的任意开集O，O⟺F(x)，存在x在X中的开邻域U，使得任意x′∈U，有O⟺F(x′)，则称F在x是上半连续的；(2)如果对于Y中的任意开集O，O∩F(x)≠φ，存在x在X中的开邻域U，使得任意x′∈U，有O∩F(x′)≠φ，则称F在x是下半连续的；(3)如果F在x既上半连续又下半连续，则称F在x是连续的；(4)如果对任意x∈X，F(x)是紧集，且F在x是上半连续的，则称F是一个usco映射。

集值映射f的图像记为:

Graphf={(x,y)|y∈f(x),x∈X}。

引理3[11]设X紧Hausdorff拓扑空间, 集值映射f:X→2X为闭值上半连续的当且仅当Graphf闭。

引理4(Fort定理)[12]设X为Hausdorff拓扑空间, Y为度量空间, f:Y→2X为紧值上半连续映射, 则使存在X的剩余集Q, 使得F在Q上下半连续。

进而, 若Y还是完备的, 则Q是稠密的。此时称F是通有下半连续的, 也即是通有连续的。

2 主要结果

本节总是设X为赋范空间的一非空紧子集, 定义集合:

M={G:X→2X|G为闭值上半连续KKM映射}。

∀G1,G2∈M, 定义距离:

ρg(G1,G2)=Hd(GraphG1,GraphG2)。

其中Hd(·,·)为Hausdorff距离。

定理1 (M,ρg)为完备度量空间。

证明: 设{Gn}为M中任意一个Cauchy序列, 于是Gn为闭值上半连续映射。根据引理3可知, GraphGn为X×X中的紧集, 所以{GraphGn}为(K(X×X),Hd)中的一Cauchy列。由引理1知, 必存在某一紧集D2∈K(X×X)，使得

grap(Gn)→D2。

定义集值映射:

G(x)={y|(x,y)∈D2,x∈X}。

显然, G为X上的闭值上半连续映射。

下面证明G为KKM映射。

假设G不是KKM映射, 则存在

x1,x2,…,xm∈X,

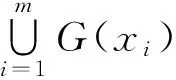
{(xj,x0)}∈GraphGnj

由引理2可知, 必有{(xj,x0)}∈GraphG, 即x0∈G(xj), 这与假设矛盾, 故(M,ρg)为完备度量空间。

对于任意G∈(M,ρg), 由KyFan定理[3]可知, KKM点总是存在的。

定义1设X为赋范空间的一非空紧子集。

(1) 对于G∈M，称点y∈F(G)是关于M的本质KKM点, 如果对y的任意邻域U(y), 都存在δ>0,使得对每一G′∈M,只要

ρg(G,G′)<δ

就有F(G′)∩U(y)≠φ成立；

(2)称G关于M是本质的, 如果每一个y∈F(G)都是关于M的本质KKM点。

由定义1及下半连续和连续的定义可得以下结论。

引理5 (1) G关于M是本质的当且仅当F在G是下半连续的；

(2) 若F在M是上半连续的, 则F在G处连续当且仅当G关于M是本质的。

定理2 F为M上的usco映射(即是紧值上半连续映射)。

证明: 因为∀x∈X,G(x)为紧度量空间X中的闭集, 所以F(G)为紧集。

下面证明F为M上的上半连续映射。

这样就得到一个收敛于G0的Cauchy列{Gn}。由yn∈F(Gn)可知

X×{yn}⊂GraphGn

且{X×{yn}}为X×X中的紧子集列。由X×X中的度量定义及引理1可知，{X×{yn}}存在收敛子列{X×{ynk}}收敛于X×{y0}。

不妨就设为{X×{ynk}}收敛于X×{y0}, 则必有X×{y0}⊂GraphG0。

如果X×{y0}⊄GraphG0，则存在

(x0,y0)∈X×{y0}

但(x0,y0)∉GraphG0。由上构造可知

(x0,ynk)∈GraphGnk

且(x0,ynk)收敛于(x0,y0), 及GraphGnk收敛于GraphG0。由引理2可得(x0,y0)∈GraphG0。

所以X×{y0}⊂GraphG0,即y0∈F(G0)。

故{ynk}为收敛于y0的Cauchy列, 这与假设F(G0)⊂U但yn∉U矛盾。

因此F(G)为usco映射。

由定理1、2及引理4、5可得以下主要结果。

定理3存在M的一个稠密剩余集Q, 使得对于任意G∈Q, G的KKM点均为本质点。

由于完备度量空间中的剩余集为稠密集, 因此证明了在Baire分类意义下, 绝大多数KKM映射的KKM点是本质的。

3 结论

本文在[9]工作的基础上，改进了上半连续KKM映射的扰动范围，推出了图像拓扑意义下上半连续KKM映射的KKM点集的通有稳定性，即在Baire分类意义下，绝大多数KKM映象的KKM点都是本质的。

[1]B.Knaster,B.Kuratowski&S.Mazurkiewicz, Ein Beweis des Fixpuntsatzes fur n-dimensionale Simplexe[J],Fund.Math.1929,14:132-137.

[2]S.S. Chang, Y.H. Ma, Generalized KKM theorem on H-space with applications,[J]. Math. Anal. Appl.1992,163: 406-421.

[3]W.A. Kirk, B. Sims, G.X.Z. Yuan, The Knaster-Kuratowski and Mazurkiewicz theory in hyperconvex metric spaces and some of its applications[J], Nonlinear Anal. 2000,39: 611-627.

[4]L. Deng, X. Xia, Generalized R-KKM theorem in topological space and their application[J]. Math. Anal. Appl. 2003,285: 679-690.

[5]M. Fang, N.J. Huang, Generalized L-KKM type theorems in topological spaces with an application[J], Comput. Math. Appl. 2007,53:1896-1903.

[6]M. Balaj, L.J. Lin, Equivalent forms of a generalized KKM theorem and their applications[J], Nonlinear Anal. 2010,73:673-682.

[7]Ky Fan, A generalization of Tychonoff’s fixed point theorem[J], Math.Ann. 1961,142:303-310.

[8]向淑文,杨辉. 集值映象的图像拓扑与不动点的通有稳定性[J] . 应用数学学报,2001(24A):221.

[9]Jian.Yu,Shu-wen.Xiang, The stability of the set of KKM points[J]. Nonlinear Anal. 2003 (54):839-844.

[10]周永辉,向淑文. 图像拓扑下Ky Fan引理解集的本质连通区及其在对策论上的应用[J].应用数学学报,2005(28):281-287

[11]Klein.E, Thompson A. Theory of correspondences[M]. New York: Wiley, 1984.

[12]Fort.M.K.JR, Points of continuity of semi-continuous functions[J]. Publications Math. Debrecen. 1951,2:100-102.

[13]Xiang S W, Jia W S, He J H, et al. Some results concerning the generic continuity of set-valued mappings[J]. Nonlinear Analysis,2012,75(8):3591-3597.

The Generic Stability of the Set of KKM Points in the Sense of Graph Topology

YANG Yan-long1，CHEN Zhi-you2

(1.College of Computer Science and Technology, Guizhou University, Guiyang 550025, China; 2. College of Mathematics and Information Science, Guiyang University, Guiyang 550005, China)

In this paper, we prove that KKM mappings with upper semicontinuous are generic stability with respect to the graph topology, i.e, in the sense of Baire category, for most KKM mappings, all their KKM points are essential. First, we define a Hausdorff-metric space M consisted of all upper semicontinuous KKM mappings, and prove that M is a complete metric space. Then we denote by F(G) the set of all KKM points of G, using of usco approach, and prove that F is compact and upper semicontinuous, therefore, obtain that F is generic stability on M by use of Fort theorem.

graph topology; generic stability; essential KKM point; residual set; upper semi-continuous

2014-05-20

国家自然科学基金资助项目：“基于有限理性的Nash平衡精炼与群智能算法研究”(项目编号：11561013)；贵州省科技厅基金项目“T-凹空间中若干非性问题的研究”(项目编号：黔科合J字[2014]2005); 省科技联合计划项目：“T-凹空间中集值映射弱Ky-Fan点的存在性研究”(项目编号：黔科合LH字[2015]7298)。

杨彦龙(1980-)，男，河南临颍人，讲师、硕士。主要研究方向：非线性分析与对策论。

O177.91

A

1673-6125(2016)03-0001-03