基于分型理论的四川秦巴山区城镇体系研究
成受明, 李宸强, 陈春华
(四川大学 建筑与环境学院, 四川 成都 610225)
基于分型理论的四川秦巴山区城镇体系研究
成受明, 李宸强, 陈春华
(四川大学 建筑与环境学院, 四川 成都 610225)
秦巴山区被列为我国11个连片特困地区,在我国“十三五”精准扶贫工作的背景下,对四川秦巴山区城镇体系的研究具有重要意义。基于非线性科学分形理论以及GIS相关软件的运用,对四川秦巴山区城镇体系的城市首位度、规模等级分形特征、空间向心性分形、均衡性分形、关联性分形等方面进行分析,得出四川秦巴山区城镇体系具有明显的分形特征,但是首位城市不突出、城镇体系呈现扁平,以通川区为中心的集聚性显著,城镇空间分布结构不紧凑,交通网络发育度亟待提高。以上结论可以为四川秦巴山区城镇规划提供有针对性的理论依据和引导对策,为同类型地区城镇体系研究提供科学参考。
分形;位序-规模分布;城镇体系;四川秦巴山区
1 引言
对于城镇体系进行分析研究,是相关层面规划编制的重要依据。传统方法主要针对城镇规模位序的量化分析,对城镇的空间分布只能做定性分析。将分形方法引入城镇体系层面中,结合传统方法可以定量地对城镇体系的人口规模等级、空间分布结构进行描述与分析,使不同城镇体系间定量对比成为可能,具有丰富的实践意义。
分形指这样的体系,该体系以某种方式与该体系的一些组成部分类似[1]。20世纪70年代,基于对目标形体上自相似性与标度不变性进行测量,美籍数学家 Mandelbrot 提出了分形理论:根据分形体的不同特征,分形理论引入分形维数这种新测度,并利用分形维数对不同分形体进行描述和比较。分形理论的建立,对描述非线性的、具有高度复杂结构的系统提供了有力的理论支撑。Mandelbrot 在分形理论建立之时,曾应用分形理论,对城市群中的城镇位序规模分布,做过分形维数性质的探讨[2]。目前,分形理论的应用早已不局限于数学领域。在城市地理学方面,许多学者对此作出了广泛的探索,并提出通过分形方法计算空间关联牛鸦比、空间关联维数与随机聚集维数等相关指标与计算方法,以建立等级规模结构与空间分布特征做出定量描述的方法。虽然分形理论在城镇体系研究中开始得到应用,但大多数仍处于较为初级的阶段,城市地理学中的分形理论仍有较大发展空间。
四川秦巴山区属于国家级连片贫困地区之一。在《秦巴山区区域发展与扶贫攻坚规划(2011-2020年)》的指导下,在保护秦巴山区的自然资源的前提下,合理利用现有资源并有针对性的投入生产建设,促进该区域的社会经济发展,切实提高人民生活质量,对地区发展和生态保护都有重要意义。对四川秦巴山区城镇体系进行研究,能为该地区新型城乡建设提供有力的理论与实践依据。
本文以四川秦巴山区为例,基于RS与GIS,通过分形理论对目标地区城镇体系的规模等级特征和空间上的分布特征作出定量的判断与分析,得出四川秦巴山区城市规模与空间分布均具有明显的分形特征,但首位城镇不突出、城镇间空间分布结构较为松散,交通网络发育成熟度不足等结论,为研究地区后续的规划与发展提供了依据。
1.1 研究范围
秦巴山区四川省部分位于四川省东北。该地区与甘肃省、陕西省及重庆市相邻接,位于成渝与关中天水经济区之间。地区涉及四川省五市共25个县市区,分别分布在绵阳市、广元市、南充市、达州市、巴中市(图1)。地区现总体城镇化率约39.4%。
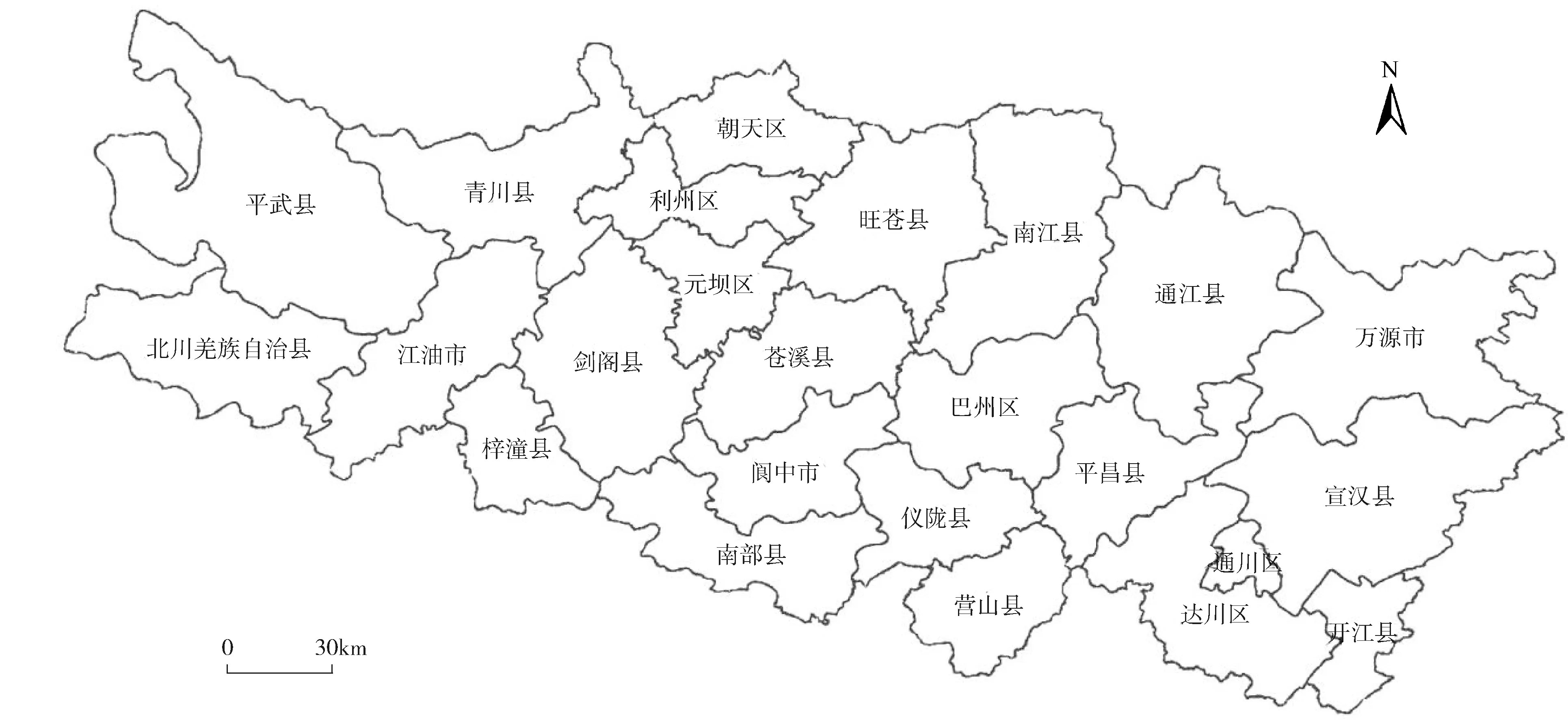
图1 四川秦巴山区各县市区区位
1.2 研究方法
首先计算四川秦巴山区首位度,其次针对城镇体系等级结构的分形特征,利用刘继生、陈彦光等学者提出的Zipf维数,来衡量城镇体系中规模分形的特征[3]。同时针对城镇体系空间结构的分形特征,提出使用聚集维数、网格(聚集)维数、关联维数3种分形维数来对空间结构分形特征进行衡量。其中利用聚集维数描述给定中心的前提下,系统内其他城镇围绕该中心的聚集状态;利用网格(聚集)维数描述系统内城镇空间上的构造特征;利用关联维数描述区域内城镇间实际的交通可达性,如果实际交通距离越接近于直线距离,则关联维数越接近于1。
2 四川秦巴山区城镇体系规模等级特征
2.1 城市首位度
根据 M.Jefferson 的城市首位度理论[4],可以计算出四川秦巴山区首位指数。城市首位指数一般包括二城市指数S2、四城市指数S4和十一城市指数S11。在四川秦巴山区区域内,将达州市达川区与通川区的连片建成区作为达州市主城区计算,但由于广元3个市辖区利州区、朝天区、昭化区三者之间、巴中巴州区、恩阳区二者之间相距较远,联系不紧密,故仍对其进行单独计算[5]。根据四川秦巴山区各市县区统计公报及相关统计年鉴查询城镇人口数据,将2014年统计城镇人口数据代入公式计算,则有:
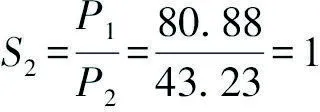
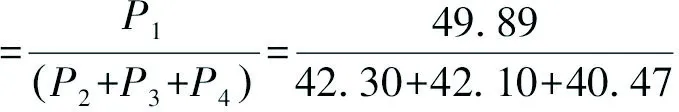
按照城市首位率,理想状况下的二城市指数S2=2,而四城市指数S4和十一城市指数S11均为1。2014年四川秦巴山区S2<2,首位城市不突出。同样S4和S11也均小于1。由此可见四川秦巴山区并不属于典型的首位分布的城镇体系结构,区域内并没有较为突出的首位城市,同时根据秦巴山区各城镇人口分布变化曲线(图2),可以得出地区城镇体系略显扁平。
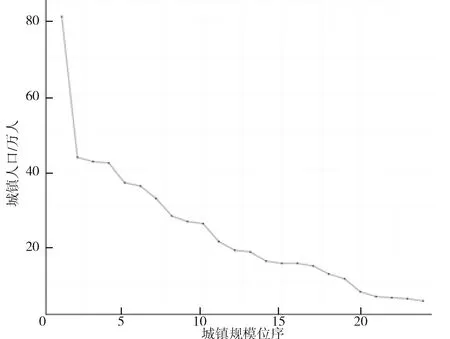
图2 2014年四川秦巴山区各城镇人口分布变化曲线
四川秦巴山区各市县区的城镇常住人口规模分布达州市主城区显著高于其他市县区,地级市主城区广元市利州区、巴中市巴州区与距离成都平原较近的县级市江油市的城镇人口均在40万人以上。而位于高海拔地区的北川、平武、青川3个县或自治州及新设立的市辖区广元朝天区、昭化区城镇人口则不足10万人。
2.2 城镇规模分形特征分析
一定区域范围内的城镇,其人口自然规模大致呈梯度分布。根据齐夫定律,理想状况下,一个城镇在区域中的的位次,与该城镇人口数量规模的乘积通常为一个定值,该固定值即为区域内首位城镇的人口数目。即
Pr=P1r-q
(1)
对公式(1)两边都取对数可得:
lnPr=lnP1-qlnr
(2)
式中:该地区第r位城市的人口规模为Pr,P1为该地区位次靠前的城市人口规模,q为需测算Zipf维数。
分别整理2014年各市县区的城镇人口数据,按规模由大到小排序,可得城镇位序1,2,3,4,…,25并计算出每个城镇的位序、规模对数,绘制城镇体系位序-规模双对数lnr-lnPr坐标图。对lnr-lnPr进行一元线性回归后,可得回归方程lnPr=-0.8341lnr+4.7951,R2=0.828,即q=0.8341。
当Zipf维数q=1时,说明城镇体系内各个城镇规模完全符合Zipf定律,即城市在城镇体系中的位次与其规模呈反比;Zipf维数越小,表明城镇体系中中等位次的城镇数量较多,体系内城镇的规模分布显得松散、等级差异较小,首位城市不突出;Zipf维数接近于0时,地区内会呈现城镇体系规模结构松散,体系发育度较低,各个城镇以自身的原始扩张为主,城镇之间的关联性弱的状态;当Zipf维数q=0时,说明该城镇体系内各个城镇规模完全一致,没有差异(图3)。
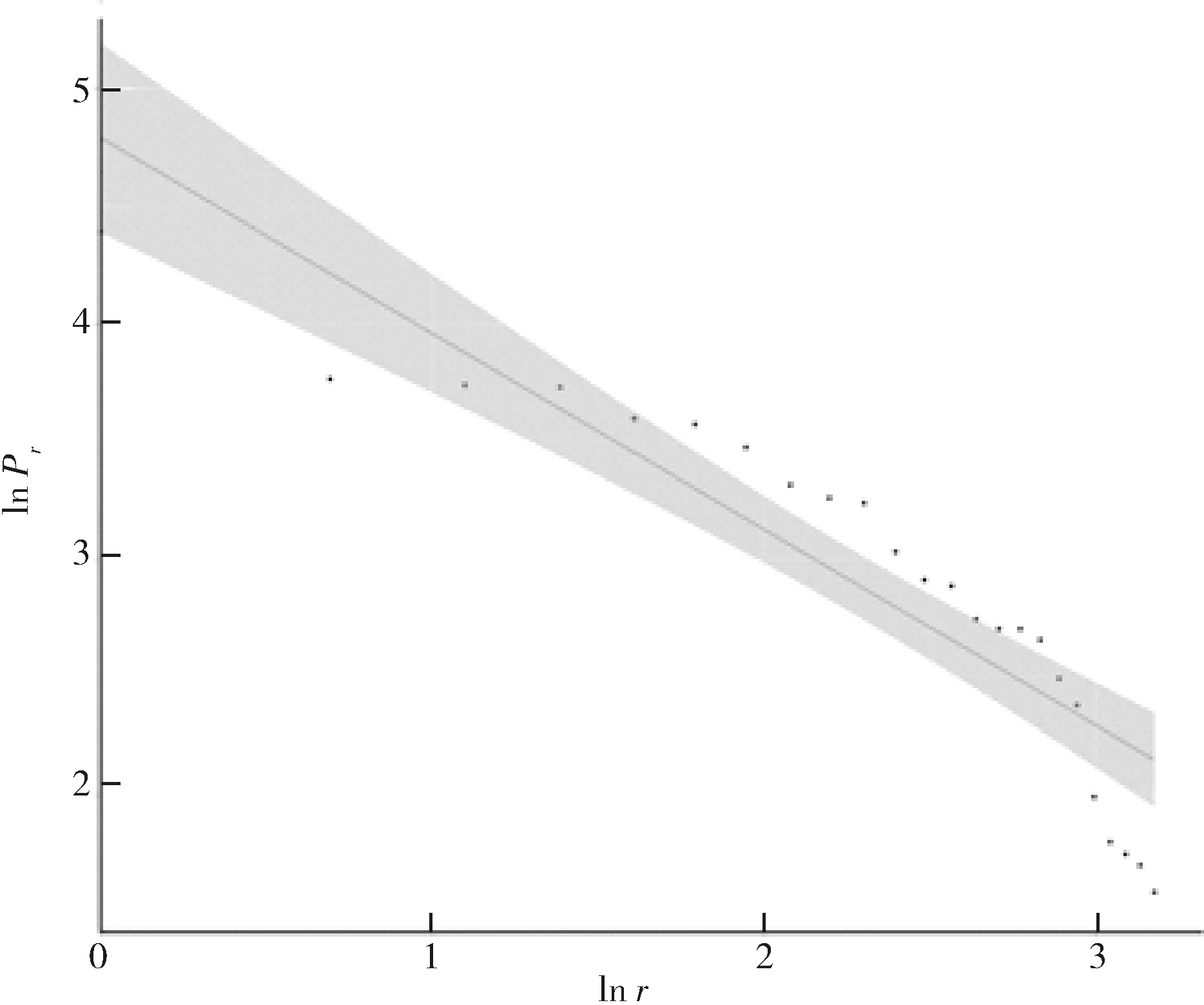
图3 四川秦巴山区城镇体系位序-规模双对数坐标
四川秦巴山区城镇体系Zipf维数q=0.8341<1,说明四川秦巴山区的等级规模分形特征较为明显,基本符合Zipf定律。对比渝东北三峡库区Zipf维数q=1.047[6],说明区域内城镇规模的分布存在较大的合理优化空间。
2.3 小结
四川秦巴山区城镇的等级规模结构距理想模型存在一定差距:城镇体系稍显扁平,中心城镇(区)不明显,以人口在40万人以下,中小城镇偏多。实际面积多数位于高原地区的平武县、北川羌族自治州,其人口与四川秦巴山区城镇体系中的其他县市差异较大。虽然二者在行政划分上同属秦巴山区城镇体系,但由于城镇体系内自然条件与交通条件条件的异质性,使得四川秦巴山区城镇体系的位序规模分布与理想状态下的幂律分布略有差异。
3 四川秦巴山区城镇体系空间结构分形特征分析
3.1 空间向心性分形
3.1.1 模型概述
在空间分布上,城镇体系中的城镇分布关系可以通过向心维数表示。理想状况下,城镇体系按照某种自相似规则围绕中心城镇呈凝聚态分布,且是各向均匀变化的[7]。则可借助空间上的几何测度关系确定城镇数目N(r)与相应半径r的关系,则有:
N(r)∝rD
(3)
式中:r为半径,N(r)表示以城镇体系中的某点为圆心;半径为r的空间范围内的城镇数量;D为向心维数。同时取两边对数可得:
lnN(r)=Dlnr+k
(4)
式中:k为常数。当D=2时,表明城镇体系的要素分布在半径上是均匀的,D值接近于2,表明该区域城镇分布越均匀;D<2时,表明城镇沿着半径方向呈聚集状态分布,城镇在空间分布上是从中心向四周是密度逐步递减的,即该体系在空间上具有向心特征;反之则表明城镇体系中城镇的空间分布密度递增,中央稠密而周边稀疏,即具有离心特征。
3.1.2 分析与结论
因秦巴山区首位城镇不明显,故为进一步确定秦巴山区向心中心,选取区域内主要城市的中心城区:广元市利州区、巴中市巴州区、达州市通川区作为测算中心。分别以以上城镇为中心,测量其他城镇到中心城镇的距离,在RStudio中将点(r,N(r))绘成lnr-lnN(r)双对数坐标图,线性回归后,求向心维数(表1,图4)。
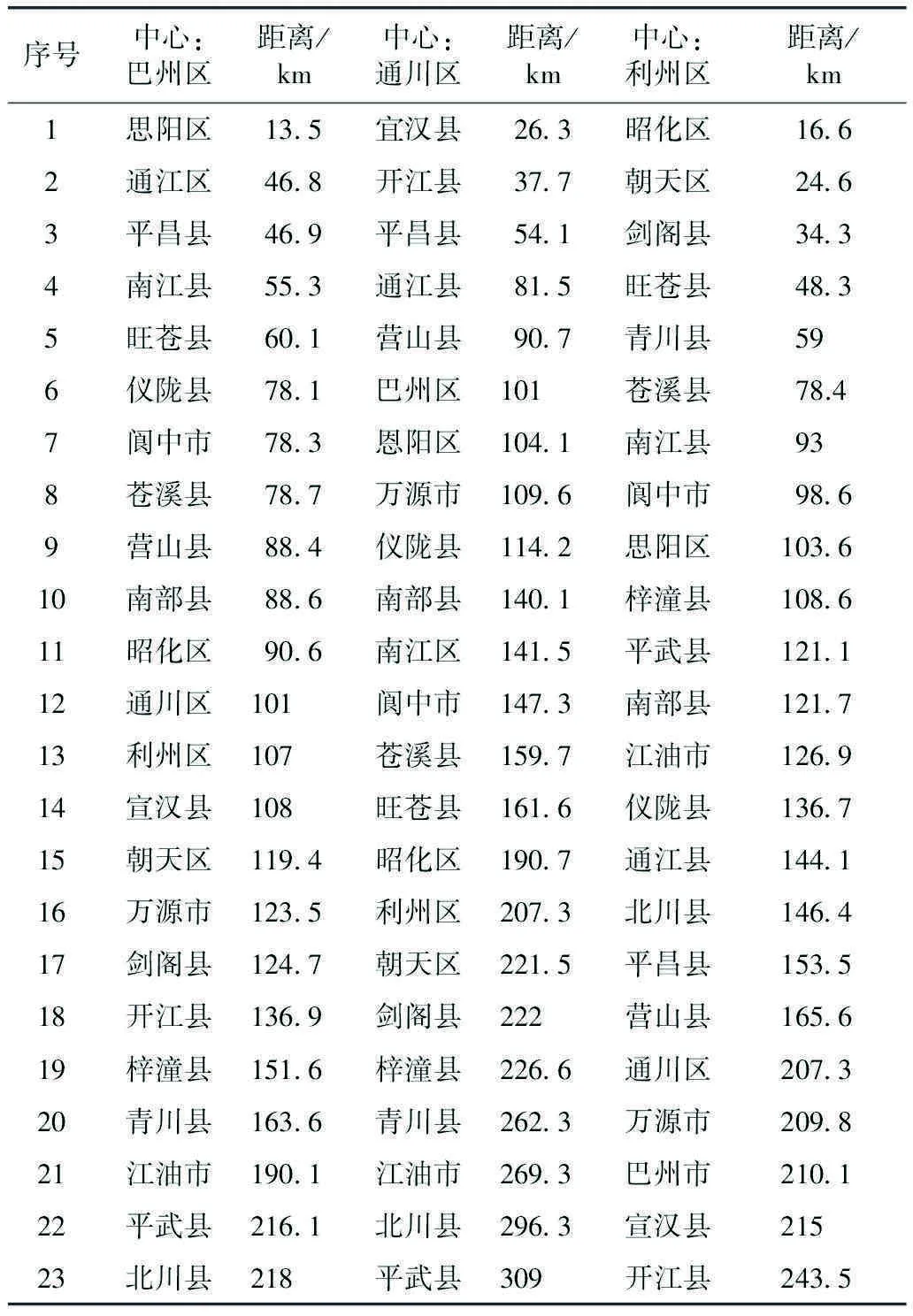
表1 区域城镇半径与数量
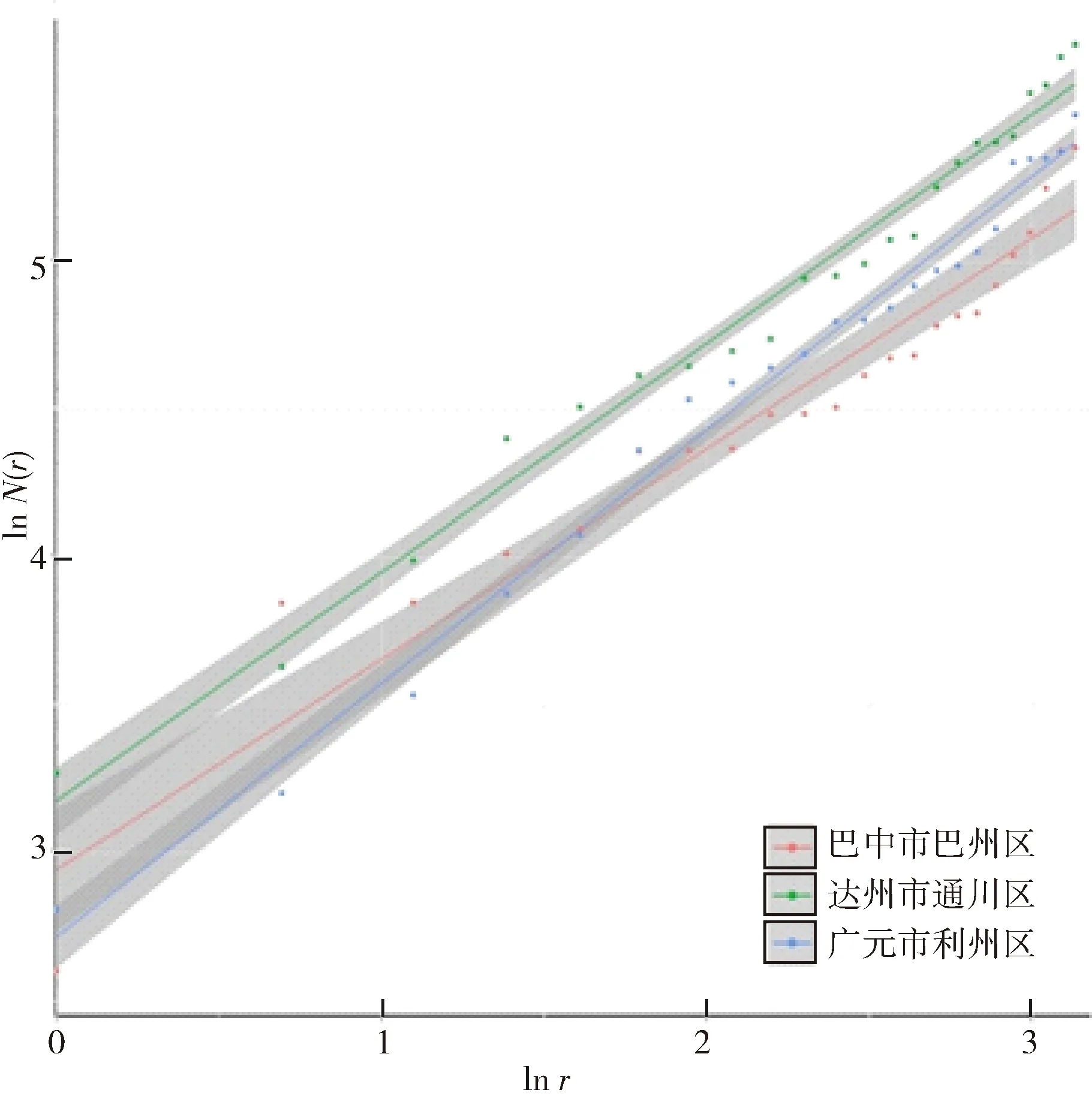
图4 四川秦巴区域镇体系半径-数量双对数坐标
以广元市利州区为中心城镇进行向心测算时,得到向心维数D=0.8556,判定系数R2=0.9867;以巴中市巴州区为中心城镇进行向心测算时,得到向心维数D=0.7108,判定系数R2=0.9315;以达州市通川区为中心城镇进行向心测算时,得到向心维数D=0.7224,判定系数R2=0.9818。
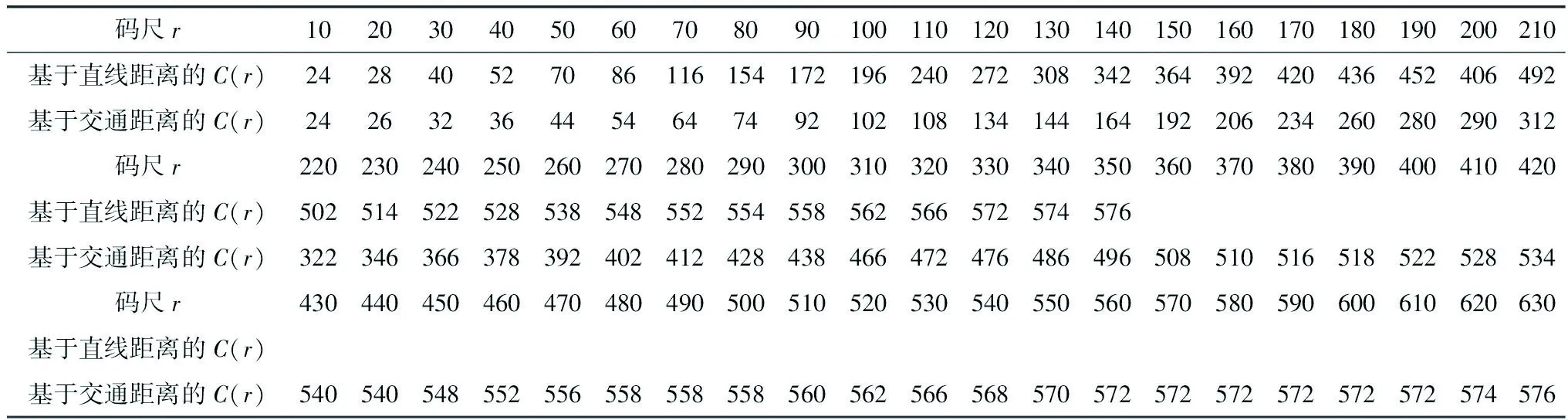
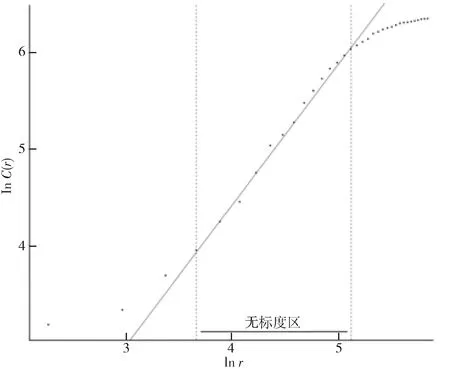
以上述3个地级市的中心城区为圆心进行测算时,向心维数均小于1,说明四川秦巴山区城镇体系中,城镇分布密度由中心向周边逐步衰减,即沿半径方向呈凝固态分布,且空间向心性明显。由于D巴中市 3.2 空间均衡性分形 3.2.1 模型概述 (5) (6) 依公式(6)对城镇体系中的所有城镇进行综合测算,得出均衡维数D。当D=0时,说明体系内中测算要素基本集聚于一点;当D=1时,表示区域内城镇沿一条地理线平均分布,0 3.2.2 分析与结论 表2 四川秦巴山区城镇体系码尺与关联数目 图5 四川秦巴山区城镇体系码尺-空间关联累积双对数坐标 3.3 空间关联性分形 3.3.1 模型概述 在城镇体系中,城镇之间的关联维数,与交通网络的通达性有着密切的关系,可以用来作为衡量城镇间交通连接水平的指标。当地区内部交通越成熟时,其以实际里程测算的关联维数将越接近以直线几何距离测算的关联维数。假设城镇间的关联距离存在分形特征时,则其空间关联函数[3]为: (7) (8) 式中:k为常数,当以直线距离作为城镇之间的关联距离时,分维数Db反映的是城镇体系的空间分布特征;当以实际交通里程作为关联距离时,分维数Dt反映的是城镇之间交通网络的连通性。为测算城镇体系交通网络通达水平,定义网络发育度ρ为: ρ=Dt/Db (9) 由于0≤Dt≤2,Dt≤Db,一般有0<ρ≤1。通常情况下,ρ值越大表明城镇体系中各城镇之间的网络连通性越好;当ρ=1时为理想状况,即每个城镇之间均为直线式连通,在现实情况中一般不存在[8]。 3.3.2 分析与结论 图6 秦巴山区城镇体系码尺-交通距离关联累积双对数坐标 3.4 小结 由分析可得,四川秦巴山区城镇体系关联性向心维数小于0.85,对比广西省城镇体系(关联维数ρ=0.928)、汉中经济区(关联维数ρ=0.9528)[9],可以发现,秦巴山区网络发育度相对不足[10],同我国西部其它地区对比稍显劣势,而同成都平原地区等我国发达地区相比,秦巴山区非均衡性明显不足,通达性较弱(表3)。 表3 四川秦巴山区分形研究数据汇总 通过上文基于分形理论的测算方法,可以发现,四川秦巴山区城镇体系结构有着显著的分形特征;其自身相似结构也体现的较为完整。通过计算Zipf维数及城市首位度,发现秦巴山区城镇体系扁平,中心城市不突出;通过计算城镇体系中的空间向心维数,发现四川秦巴山区以达州市通川区为中心的集聚性更显著;通过计算均衡维数,发现均衡维数D接近1.5,说明四川秦巴山区具有空间非均衡性,但非均衡性较弱;通过计算关联维数,得出四川秦巴山区通达性较弱。针对以上特点和问题,笔者认为四川秦巴山区城镇发展的策略应是在发挥沟通成都、西安两个超大城市及其周边地区的作用的基础上,实现内部城镇职能的合理分工,有梯度的建设大型城市和中小城市,并应对小城镇的发展投入合理支持。 [1]陈彦光.分形城市系统:标度· 对称· 空间复杂性[M].北京:科学出版社, 2008. [2]黄亚平,刘凌云.湖北县域城镇化自组织过程,机制与分形研究[J].城市规划,2015,(5):16-25. [3]刘继生,陈彦光.城镇体系等级结构的分形维数及其测算方法[J].地理研究,1998,17(1):82-89. [4]许学强,周一星,宁越敏,等.城市地理学 (第二版)[M].北京:高等教育出版社,2009. [5]姜世国.都市区范围界定方法探讨[J].地理与地理信息科学,2004,20(1):67-72. [6]朱邦耀,宋玉祥,李汝资,等.基于分形理论的渝东北三峡库区城镇体系研究[J].华中师范大学学报:自然科学版,2015,49(3):447-451. [7]曹芳东,吴江,徐敏.基于分形理论的江苏省南通市城镇体系空间结构研究[J].人文地理,2010,(5):69-74. [8]周恺.长江三角洲高速公路网通达性与城镇空间结构发展[J].地理科学进展,2010,29(2):241-248. [9]朱士鹏,徐兵,毛蒋兴.广西城镇体系空间结构分形研究[J].热带地理,2010,30(2):178-182. [10]王武林,杨文越,曹小曙.中国集中连片特困地区公路交通优势度及其对经济增长的影响[J].地理科学进展,2015,34(6):665-675. A Fractal Study on the Urban System of Qinba Mountain in Sichuan CHENGShou-ming,LIChen-qiang,CHENChun-hua (School of Architecture and Environment,Sichuan University,Chengdu 610225,China) Qinba Mountain was listed as one of the 11 Contiguous-destitute-areas.In the context of precise poverty alleviation in the thirteenth Five-year-plan,the study of the urban system in Qinba mountain area has great significance in China’s thirteenth Five-year-plan.Based on Nonlinear Science fractal theory and GIS software use,this paper computs and analyzes the urban Qinba mountain towns system of Primate City Degree,rank-scale fractal,space concentric fractal,balance fractal,and relevance fractal etc.then,concludes that there are obvious fractal features of urban system in Qinba Mountain,but the degree is not obvious; the structure of urban system is flat; cities distribute significantly in the center of Tongchuan District.However,the spatial distribution of cities is not compact,and the development of transportation networks needs to be improved.These conclusions can provide targeted theoretical basis and the countermeasures for the Qinba mountain town planning,providing scientific reference for the study of similar urban system. fractal;rank-scale distribute;urban system;Qinba Mountain 10.3969/j.issn.1009-4210.2016.06.016 2016-10-21 中国工程院重大咨询项目 (2015-ZD-05-09-05);四川省发改委重点课题项目 (ZH2015038) 成受明(1976—),女,讲师,从事城乡规划与人居环境研究。E-mail:1003433351@qq.com 陈春华(1975—),女,讲师,从事城乡规划研究。E-mail:171486115@qq.com F301.1(271) A 1009-4210-(2016)06-108-07

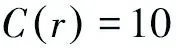

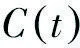

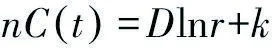



4 结论

