一种新的模糊控制多模型算法在目标跟踪中的应用
国 强, 贺紫兰
(哈尔滨工程大学 信息与通信工程学院, 哈尔滨 150001)
一种新的模糊控制多模型算法在目标跟踪中的应用
国 强, 贺紫兰
(哈尔滨工程大学 信息与通信工程学院, 哈尔滨 150001)
为解决传统的蛇形建模方法不能反映出反舰导弹典型运动特性的问题,引入动力学建模方法研究弹道问题,把导弹视为可控质点,建立了反舰导弹末端蛇形机动弹道模型. 采用被动传感器进行跟踪,提出一种新的基于模糊控制的交互式多模型自适应无迹卡尔曼滤波算法,根据Sage-Husa噪声统计估值器的原理提出了状态误差协方差自适应算法,克服了传统噪声自适应算法在目标发生强机动时收敛速度慢的缺点,同时利用模糊控制方法实现了实时调整交互式多模型算法中的转换概率矩阵. 仿真实表明:所建立的弹道模型对探测、识别和跟踪反舰导弹技术的研究有一定的参考价值;改进的跟踪算法能够快速调整模型概率,使得其估计误差的收敛速度比交互式多模型算法更快,鲁棒性更强,并且能够有效降低纯方位目标跟踪的误差,实现对反舰导弹末端蛇形弹道模型的稳定跟踪.
目标跟踪; Sage-Husa噪声统计估值器; 无迹卡尔曼滤波; 模糊逻辑交互式多模型算法
目前反舰导弹已成为现代海战最重要的攻击性武器,蛇形机动是反舰导弹的典型运动方式之一,具有运动速度高、突防能力强、打击威力大等特点,因此加强舰船的反导能力有重要的意义. 在目标跟踪领域中对反舰导弹的研究还是有限的,尤其是将运动轨迹与跟踪相结合的研究少之又少. 本文采用动力学建模[1]方式,对反舰导弹蛇形机动轨迹进行仿真. 对于三维空间蛇形机动目标的跟踪,常常因为传统模型不匹配而导致雷达跟踪精度低,在被动雷达[2]跟踪的情况下甚至导致发散. 本文根据蛇形机动模型的运动规律,实现对其典型运动模式的分析与建模,并得到与模型匹配的三维空间蛇形机动目标模型.
在机动目标跟踪中采用交互式多模型算法,并提出一种基于模糊逻辑[3-4]的交互式多模型自适应无迹卡尔曼滤波算法FLIMM-AUKF(adaptive unscented Kalman filter of fuzzy logic interacting multiple model). 在滤波算法中对Sage-Husa噪声估值器进行了改进,文献[5]中给出了常规的推导过程,文献[6-8]将Sage-Husa噪声估计与无迹卡尔曼[9]、粒子滤波[3]等结合,提出了自适应算法. 本文针对其进行改进,提出了基于误差协方差估计的无迹卡尔曼滤波算法,通过对蛇形模型的跟踪仿真验证了该算法收敛速度快、误差小,具有实用价值.
1 导弹弹道的动力学建模
1.1 反舰导弹运动特性分析
反舰导弹从发射到命中目标的整个过程大致分为4个阶段:发射阶段、巡航阶段、搜索阶段和自导命中阶段. 导弹发射后先以小角度爬升,借助于助推器飞行,助推器加速到冲压发动机接力速度后脱落. 完成转级后,冲压发动机给导弹加速,可达到2~5 Ma. 然后在高度表控制下,导弹降至巡航高度上平飞. 在离目标一定距离时转入水平“蛇行机动”,这一过程一般受程序自动控制. 当运动到程序设定的距离时,停止蛇行机动,按比例导引方法飞向目标,现代高性能反舰导弹的飞行高度可降至1 m,几乎是擦着浪尖飞行. 在攻击弹道末段,导弹在垂直平面进行“跃升机动”,升到一定高度俯冲攻击目标.
蛇形机动阶段为反舰导弹的搜索阶段,该阶段直接影响导弹能否发现目标. 本文针对反舰导弹典型的运动蛇形机动进行弹道仿真.
1.2 导弹弹道的动力学建模方法
反舰导弹的运动规律一般采用六自由度空气动力学模型来描述,但是由于在很多情况下气动数据是无法得到的,而且六自由度运动方程模型中需要求解多个高阶微分方程,计算量和数据存储量都大,在战场环境仿真中难以实现. 因此,按照导弹运动规律,规划出导弹升力、推力和侧力,由导弹质心运动方程求出导弹位置和姿态,进而生成导弹航迹.
为方便导弹弹道的动力学建模,首先定义以下符号:
v为导弹的运动速率,θ为导弹的弹道倾角,ψv为导弹的弹道偏角,x、y和z为导弹在惯性坐标系中的位置分量,gx2、gy2和gz2为重力加速度在弹道坐标系中3个坐标轴方向的分量,ax2、ay2和az2为导弹过载在弹道坐标系中3个坐标轴方向的分量.
以导弹为目标,现假定目标做“蛇形”机动,机动加速度按正弦规律变化,根据文献[10]可知其质心运动方程以及弹道坐标系的定义. 3个方向上的重力加速度和导弹过载如下
先采用龙格库塔法计算目标的实际运动位置,再经过坐标转换,将速度坐标系转换到弹体坐标系,对蛇形弹道进行仿真.
1.3 蛇形机动模型
目前,机动目标运动模型主要有匀速 CV 模型、匀加速 CA 模型、Singer[11]模型、“当前统计”模型和Jerk 模型[12]. 前2种运动模型一般用来跟踪弱机动目标,后3种运动模型可以跟踪较强机动目标,但误差较大,对于加速度时刻变化的情况跟踪效果仍不理想. 本文提出的蛇形运动加速度是正弦变化的,因此需要一种更好的模型与之匹配. 根据动力学建模对蛇形弹道进行了仿真,根据所提出的蛇形弹道建立与之匹配的蛇形运动模型.
“蛇形”机动模型假定目标在水平面内按正弦规律运动,目标在X轴方向做匀速直线运动,速度为vx,在Y方向上速度为0,在Z方向上做正弦运动.
离散化可得状态方程的离散化形式为X(k+1)=FX(k)+GW(k)推导出离散时间状态转移矩阵F以及矩阵G为
2 改进的自适应模糊逻辑交互式多模型算法
2.1 模糊逻辑交互式多模型算法
Blom和Bar-Shalom在广义伪贝叶斯算法基础上,提出了一种具有Markov切换系数的交互式多模型算法. 本文提出一种模型转换概率自适应的模糊逻辑交互式多模型算法FLIMM(fuzzylogicinteractivemultiplemodel),通过模糊控制算法对模型概率进行更新,使得模型概率得到迅速转换从而加快滤波系统的响应速度,达到快速收敛,并提高系统的精度.
FLIMM算法的基本步骤与交互式多模型滤波算法[4]的步骤类似,只是在对模型概率更新时引入了模糊逻辑算法进行决策,模型概率更新模块的输入变量为各个滤波器的输出Λi(i=1,2,…,n).
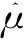
以模型1(匀加速运动模型)的概率为例,设模型概率更新模块的输入变量为I1和I2,输出变量为u,令
(1)
由于模型概率的取值范围为[0,1],通过式(1)可以得出输入变量的论域范围分别为I1: [0,1]、I2: [-1,1]、u: [0,1]. 设定了论域范围后,再在论域范围内划分输入输出变量的模糊子集.I1的模糊子集为{小(S),中(M),大(B)},I2的模糊子集为{负(N),零(Z),正(P)},u的模糊子集为{小(S),中(M),大(B)}. 在确定了输入输出变量的模糊子集后,确定每个变量的模糊子集中元素在对应变量论域范围内的隶属度. 各个变量对应的隶属度函数如图1所示.
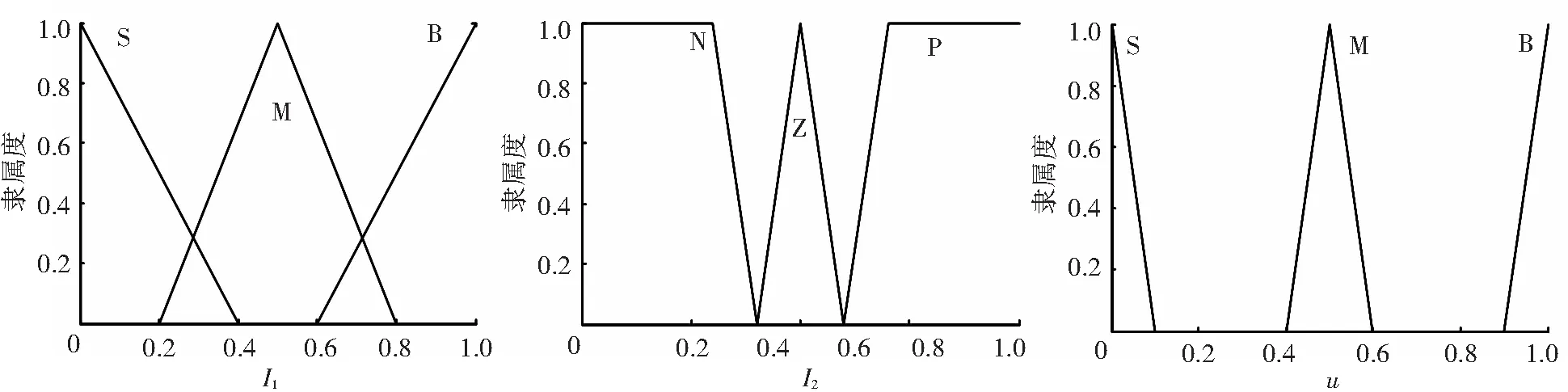
图1 I1、I2和u的隶属度函数
根据输入输出变量的含义以及经验知识可以得到如下结论:若模型概率变化为负,即I2为N,则当前模型概率u应比前一时刻模型概率I1小;若模型概率变化为零,即I2为Z,则当前模型概率u应与前一时刻模型概率I1相同;若模型概率变化为正,即I2为P,则当前模型概率u应比前一时刻模型概率I1大.
在对模糊逻辑系统的输出进行解模糊化时,采用中位数法进行解模糊化,得到模型的实际概率.
2.2 改进的误差协方差统计估值器
估计噪声统计已有许多文献报导,尤其是Sage和Husa的结果有许多应用和发展. 近年来也有将其与各种滤波算法相结合的方法,但是没有直接对Sage-Husa噪声估值器进行改进. 本文提出一种误差协方差统计估值器,原理如下:
定义非线性离散时间系统为
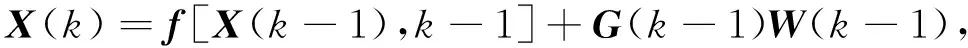

式中:X(k)为n维被估计状态向量,Z(k)为m维观测向量,W(k)为r维过程噪声,V(k)为m维观测噪声,f[·]为n维可微向量函数,G(k)为n×r维过程噪声输入矩阵,h[·]为m维可微向量函数.
误差协方差为
假设误差协方差是未知的定常向量或矩阵,自适应滤波问题就是基于观测求误差协方差和状态X(k).
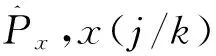
式中,X(k)={x(0),x(1),…,x(k)}, Z(k)={z(1),z(2),…,z(k)}.
由Bayes公式得
而p[Z(k)]与最优化无关,因而问题转化为求如下无条件概率密度的极大值:
J=p[X(k),Px,Z(k)]=p[Z(k)|X(k),Px]·p[X(k)|Px]·p[Px].
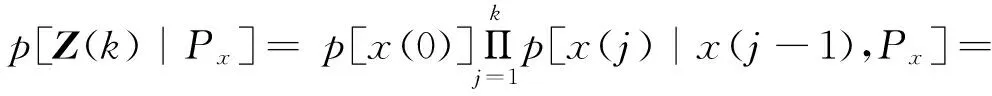
类似有
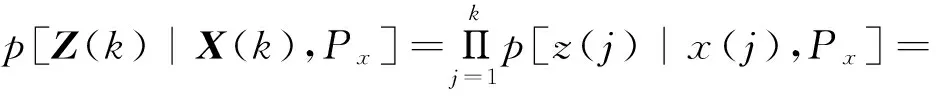
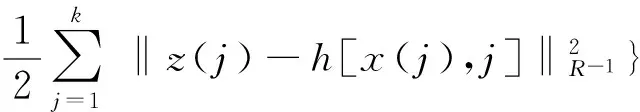
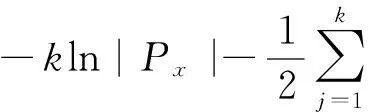
J与ln J有相同极点. 暂设x(j/k)已知,则令
可得误差协方差统计的MAP估值器为
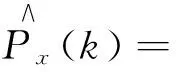
(2)
1)次优MAP估值器. 在式(2)中,以滤波估值x(j/j)或预报估值x(j/j-1)近似代替计算复杂的平滑估值x(j/k),可得次优MAP估值器为
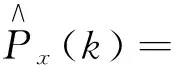
2)次优无偏MAP估值器. 由
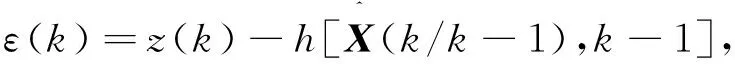
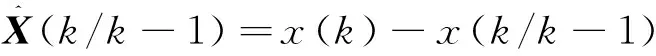
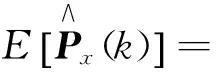
所以
引出递推无偏MAP估值器为
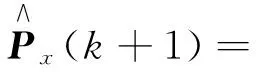
FLIMM-AUKF算法的具体步骤与IMM算法相同,并行滤波采用本文提出的自适应无迹卡尔曼滤波算法进行滤波;模型概率更新采用2.1节的模糊逻辑控制对模型概率进行更新,将2.1节中的条件输入到matlab中.fis文件,调用该文件实现对模型概率的更新.
3 仿真实验及结果分析
实验平台:因特尔i7处理器、主频2.20 GHz、64位Windows 7专业版下的Matlab R2009a仿真软件. 跟踪场景参数设置:三维情况下,目标在0~15 s做匀速直线运动,16~60 s做蛇形运动. 三维弹道模型如图2所示,目标的非线性观测方程描述如下:
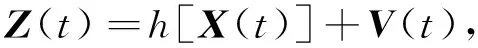
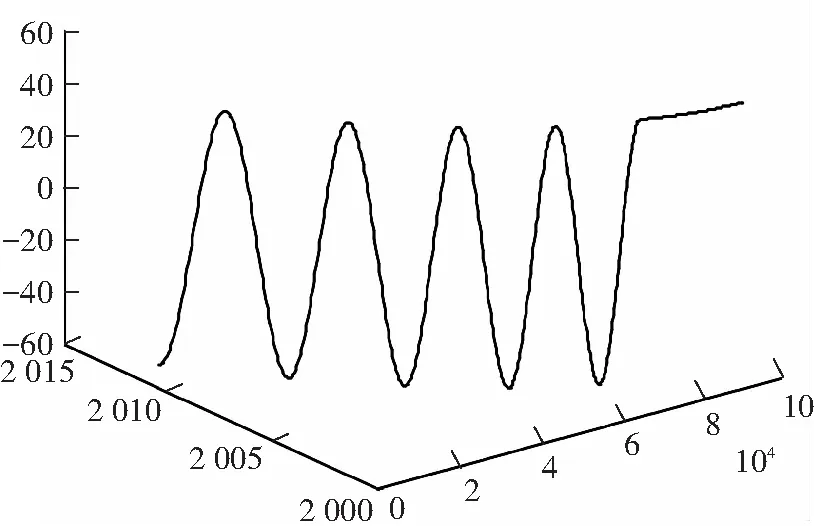
图2 目标弹道模型三维视图
假设目标的机动频率ω=0.2π已知,探测器周期为0.1 s,龙格库塔法步长为0.01 s.
算法参数设置如下:目标初始值为[90 000 2 000 50 -1450 0 0 0 0 0],2种运动模型初始概率都为0.5,初始状态误差协方差P(0)=diag{[100 100 100 25 25 25 1 1 1]},观测噪声的标准差为1 mrad,蒙特卡洛仿真次数为50次.
图3~5为分别采用本文改进FLIMM-AUKF算法、IMM-UKF算法和自适应IMM-UKF算法(文献[6]中算法)对目标进行跟踪滤波的估计误差对比图. 可以看出自适应算法和本文改进算法的误差明显小于IMM-UKF算法的估计误差. 改进的FLIMM-AUKF算法效果比噪声自适应IMM-UKF算法效果好,这是因为改进的误差协方差算法不仅对误差协方差进行了自适应,同时也对噪声进行了自适应. 并且本文改进算法在z方向上收敛速度明显快于自适应算法,误差收敛到±1,证明本文算法是可行的.
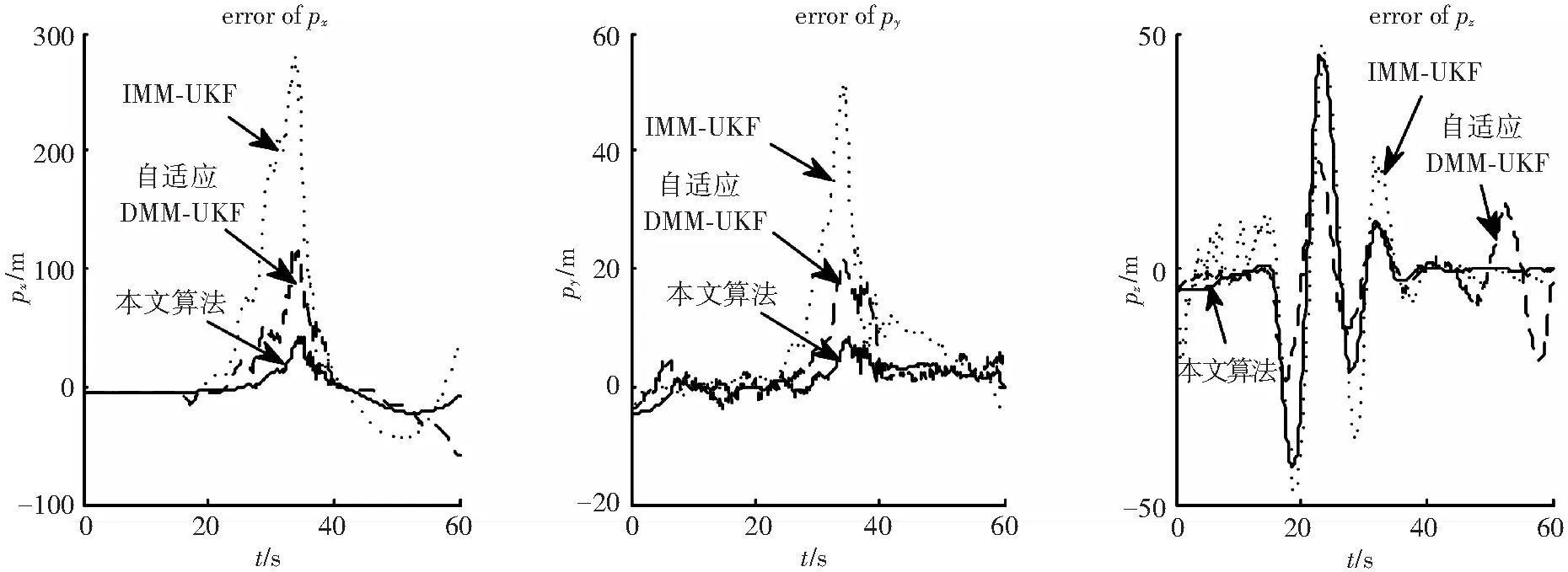
图3 IMM-UKF、自适应IMM-UKF与本文算法跟踪机动目标位置估计误差
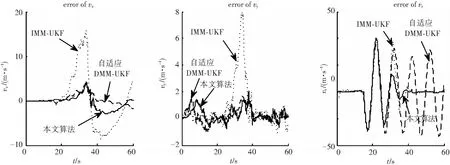
图4 IMM-UKF、自适应IMM-UKF与本文算法跟踪机动目标速度估计误差
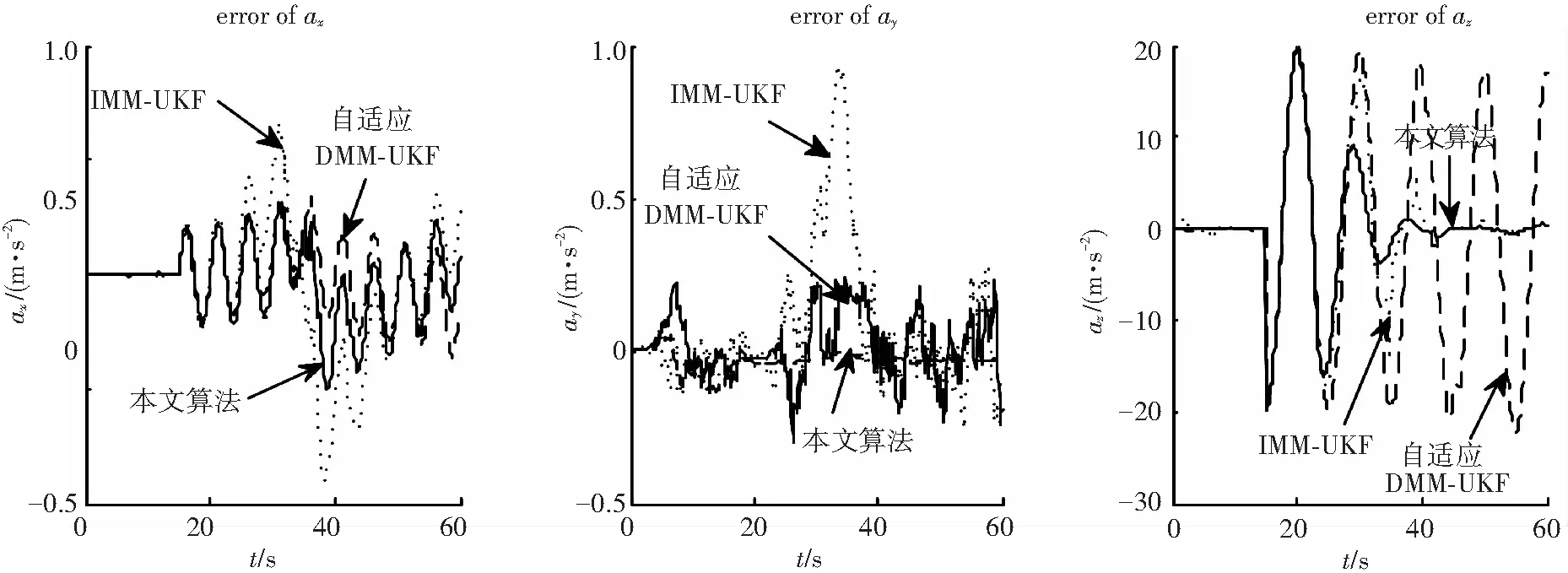
图5 IMM-UKF、自适应IMM-UKF与本文算法跟踪机动目标加速度估计误差
4 结 论
1)采用动力学建模的方法,建立了简洁实用的蛇形三维模型,所建立的弹道模型对探测、识别和跟踪反舰导弹技术的研究有一定的参考价值.
2)在模型跟踪方面,提出改进的基于模糊控制的自适应交互式多模型算法,仿真结果说明该算法在一定程度上解决了被动跟踪误差大的问题,同时也验证了蛇形建模和改进算法的合理性.
[1] Lisano M E. A practical six-degree-of-freedom solar sail dynamics model for optimizing solar sail trajectories with torque constraints[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit.Providence: AAAA, 2004.
[2] HAN Seul-Ki, RA Won-Sang, WHANG Ick-Ho,et al. Linear recursive passive target tracking filter for cooperative sea-skimming anti-ship missiles[J]. Radar, Sonar & Navigation,2014,8(7): 805-814.
[3]WANG X F, CHEN J F, SHI Z G, et al. Fuzzy-control-based particle filter for maneuvering target tracking[J]. Electromagnetics Research,2011,118:1-15.
[4] PENG D L, GUO Y F. Fuzzy-logic adaptive variable structure multiple-model algorithm for tracking a high maneuvering target [J]. Journal of the Franklin Institute-Engineering and Applied Mathematics,2014,351(7): 3837-3846.
[5]占荣辉,张军.非线性滤波理论与目标跟踪应用[M].北京:国防工业出版社,2013.
ZHANG Ronghui, ZHANG Jun. Nonlinear Filtering Theory with Target Tracking Application[M]. 2013.
[6]石勇, 韩崇昭. 自适应UKF算法在目标跟踪中的应用[J]. 自动化学报,2011,37(6):756-759.
SHI Yong, HAN Chongzhao. Adaptive UKF method with applications to target tracking[J]. Acta Automatica Sinica, 2011,37(6):756-759.
[7]李昱辰,李战明. 噪声未知情况下的自适应无迹粒子滤波算法[J].吉林大学学报,2013,43(4):1139-1145.
LI Yuchen, LI Zhanming. Adaptive unscented particle filter algorithm under unknowm noise[J]. Journal of Jilin University, 2013,43(4):1139-1145.
[8]李宁,祝瑞辉,张勇刚. 基于Sage-Husa算法的自适应平方根CKF目标跟踪方法[J].系统工程与电子技术,2014,36(10):1899-1905.
LI Ning,ZHU Ruihui,ZHANG Yonggang. Adaptive square CKF method for target tracking based on Sage-Husa algorithm[J]. Systems Engineering and Electronics, 2014,36(10):1899-1905.
[9] JULIER S J, UHLMANN J K. A new method for the nonlinear transformation of means and covariances in filters and estimators[J]. IEEE Transactions on Automatic Control, 2000, 45(3): 477-482P.
[10]李士勇, 章钱. 智能制导:寻的导弹智能自适应导引律[M]. 哈尔滨:哈尔滨工业大学出版社,2011.
LI Shiyong,ZHANG Qian. Intelligent guidance: intelligent adaptive guidance laws for homing missile[M]. Harbin: Harbin Institute of Technology Press, 2011.
[11]LIU Jinfang, DENG Zili, GAO Yuan. Covariance intersection fusion Kalman estimator for the two-sensor time-delayed system[C]//International Conference on Information Fusion. Singapore:IEEE, 2012: 1586-1593.
[12]LIU Wangsheng, LI Yaan, CUI Lin. An improved algorithm for high maneuvering target based on Jerk model[J]. Binggongxuebao,2012,33(4): 385-389.
(编辑 王小唯)
A novel fuzzy control multiple model algorithm in target tracking
GUO Qiang, HE Zilan
(College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001,China)
An innovative snakelike terminal maneuvering trajectory model of anti-ship missiles, in which the missiles are regarded as controllable mass points and can be tracked by passive sensors, is introduced to compete with the continuous penetrating enhancing of modern anti-ship missiles by adopting dynamic modeling method. A novel adaptive unscented Kalman filter algorithm based on the fuzzy control interacting multiple algorithm is proposed. The proposed algorithm can achieve the real-time adjustment of the matrix of transition probability, faster convergence rate due to the fuzzy control and state error covariance adaptive algorithm which is based on the principle of Sage-Husa noise statistical estimator. Simulation results verify the ballistic model is established for the detection, recognition and tracking of anti-ship missile technology research has certain reference value. Besides, the improved tracking algorithm can quickly adjust the probability model to bring about faster convergence speed and better robustness, which can effectively reduce the error of bearing-only target tracking and can achieve the stability and reliability of the snakelike terminal maneuvering trajectory model of anti-ship missiles.
target tracking; Sage-Husa estimators of noise statistics; unscented filter Kalman; fuzzy IMM algorithm
10.11918/j.issn.0367-6234.2016.11.019
2015-05-25
国 强(1972—),男,教授,博士生导师
贺紫兰,358174868@qq.com
TP391
A
0367-6234(2016)11-0123-06

