考虑表面形貌的腐蚀钢板疲劳缺口系数
徐善华,秦广冲,姬立星,王友德
(西安建筑科技大学 土木工程学院,西安710055)
考虑表面形貌的腐蚀钢板疲劳缺口系数
徐善华,秦广冲,姬立星,王友德
(西安建筑科技大学 土木工程学院,西安710055)
为有效模拟钢板腐蚀后的复杂形貌,得到基于真实表面形貌的钢板疲劳缺口系数,采用盐雾法对Q235钢板进行快速腐蚀试验,并对腐蚀表面进行三维测量.利用逆向工程软件Geomagic Studio和数值分析软件ANSYS建立三维腐蚀实体模型,分析表面应力分布.最终通过计算得到了疲劳缺口系数值,并将计算结果和试验结果进行对比.结果表明有限元分析结果与疲劳试验结果两者误差非常小,从而验证了模拟方法的可行性.通过Geomagic Studio可实现快速三维可视化建模,非常好地模拟腐蚀形貌特征,结合ANSYS可灵活、高效地估算各种复杂形貌构件的疲劳缺口系数.关键词: 腐蚀钢板;表面形貌;逆向工程;数值分析;疲劳缺口系数
工程实践中,腐蚀结构钢在重复荷载作用下随着服役年限增加,大大降低了材料抗疲劳性能,对现役建筑物使用寿命构成潜在威胁.由于缺口产生的应力集中是影响结构疲劳强度的主要因素之一,在疲劳强度和寿命估算中,无论名义应力法还是局部应力应变法,疲劳缺口系数Kf是一个十分重要的参数,实践证明,Kf对疲劳寿命的估算结果非常敏感[1-3].确定疲劳缺口系数最直接、最可靠的办法是通过试验获得,但疲劳试验代价大,现阶段采用数值模拟方法估算疲劳缺口系数成为方便可行的技术手段[4].
由于腐蚀表面特征具有随机性,而大部分学者仅仅通过单个或者多个腐蚀缺口进行研究[5-6],这很难对实际腐蚀所产生的应力集中对疲劳寿命的影响进行描述.目前三维形貌的获取方法大体可分为接触式测量和非接触式测量[7],其中PS50三维非接触式表面形貌仪由于测速快,应用范围越来越广泛.由于获取的三维数据点数量庞大,而直接将其导入到ANSYS中建模是非常复杂和困难的,但很多逆向工程软件的曲面模型重建可以跟ANSYS文件直接进行数据交流,如Polyworks、Imageware、Rapidform、ICEM Surfl、Geomagic Studio等[8-9].
因此,为了能够运用计算机技术真实有效地反映出腐蚀钢板的疲劳性能,本文将在试验基础上应用逆向工程软件Geomagic Studio和有限元软件ANSYS来仿真模拟研究真实锈蚀表面的疲劳缺口系数.
1 腐蚀面形貌测试
将10组设计尺寸为280 mm×50 mm×8 mm(长边沿钢板轧制方向)的Q235板材试样,以垂直方向成30°放置盐雾箱内(图1),通过配制5%(质量百分比)的氯化钠溶液(NaCl)对钢板进行快速腐蚀试验,腐蚀周期为14、28、42、56、70、84、98、118、138、178 d.
采用PS50三维非接触式表面形貌仪(图1),腐蚀试验将环氧树脂包裹1 cm作为锈蚀区域的基准面,将不同锈蚀时间的10个试件分别编号A0~A9,锈蚀钢结构腐蚀表面进行形貌测试时,每个锈蚀钢结构试件正反两面分别选择2个区域测量,每个区域测试范围是40 mm×30 mm,沿40 mm方向测试步长为18 μm,沿30 mm方向测试步长为220 μm,选择最大测量速度10 mm/s提高测试效率.通过3D分析软件可输出各个区域的三维坐标数据,绘制锈蚀表面3D形貌图.图2所示为腐蚀14、70和138 d的表面三维形貌图(一侧正面).
观察图2中的腐蚀表面三维形貌图,可以看出图中用不同的颜色将表面腐蚀特征清晰地呈现出来,颜色从白色-红色-黄色-绿色-青色-蓝色-紫色依次渐变,表明了试件腐蚀表面的腐蚀深度从低到高的变化.环氧树脂包裹的未腐蚀区域颜色基本一致且较浅,说明基本没有发生腐蚀,可为腐蚀区域提供零参考面;经过一定腐蚀时间之后,未腐蚀区域和腐蚀区域有着明显的颜色差异,腐蚀区域在三维形貌图上也具有非常明显的色差,即产生了高度差异;通过分析图像和数据可以发现,腐蚀时间较短时,主要发生点蚀,表面布满密密麻麻的小坑;随着腐蚀时间延长,腐蚀向整个表面扩展,之前的小洞慢慢连成一起,锈坑形貌也由深窄形转变为碟形,到了后期的腐蚀则有大面积剥落.

图1 盐雾箱及PS50三维测量仪器

图2 腐蚀14 d、70 d和138 d表面三维形貌图(μm)
2 腐蚀钢板疲劳缺口系数试验确定方法
2.1 试验概况
采用液压伺服万能疲劳试验机,对A0~A9这10组腐蚀试件进行疲劳试验,根据GB/T 3075—2008《金属材料疲劳试验轴向力控制方法》及 GB/T 15248—2008《金属材料轴向等幅低循环疲劳试验方法》的要求,标准试件的设计尺寸见图3.在试验过程中,选择的荷载形式为正弦波,应力比R=0.1,应力比为最小应力与最大应力比值,其中最大应力水平为260 N/mm2(取极限强度的0.6倍),加载频率为10 Hz,对试件进行单轴拉伸疲劳试验.
2.2 试验结果分析
中国常用工程机械材料的P-S-N曲线可参考文献[10].文献[11]针对Q235低碳钢标准疲劳试样进行疲劳试验研究,对不同应力幅下未腐蚀和腐蚀材料的疲劳寿命做了统计分析.平均应力σm=0(即R=-1)的光滑试样的标准S-N曲线为
logN=36.251-13.167logS.
(1)

图3 疲劳试件标准图(mm)
由于疲劳试验所用的构件尺寸小,仅有60 mm长,因此可以不考虑尺寸的影响;腐蚀试件表面缺口多,不能忽略应力集中对疲劳寿命的影响;试验加载为单轴状态,与标准试验相同,可以不考虑加载方式的影响;但是,本文试验的应力比为R=0.1,与标准试验应力比R=-1的情况相差较大,平均应力的影响不可忽略.因此,对S-N曲线修正平均应力和应力集中系数即可.
采用Goodman直线模型进行平均应力修正,该模型反映了应力幅与平均应力和疲劳极限之间的关系,经过计算得到了本文钢材应力幅与基本钢材应力幅的比值为0.682.然后进行等寿命转换,即在相同疲劳寿命时不同应力比下的疲劳极限的关系转换.最终得到了本文所需钢材S-N曲线的表达式为
logN=34.064-13.166logS.
(2)
疲劳缺口系数Kf的一般定义为:相同条件和相同循环次数下,无应力集中试件的疲劳强度Se与有应力集中试件的疲劳强度Sn之比,即[12]
(3)
分析疲劳试验并结合式(1)~(3)以及文献[13]中有关疲劳极限强度修正及疲劳缺口系数修正的计算公式,得到结果汇总见表1.
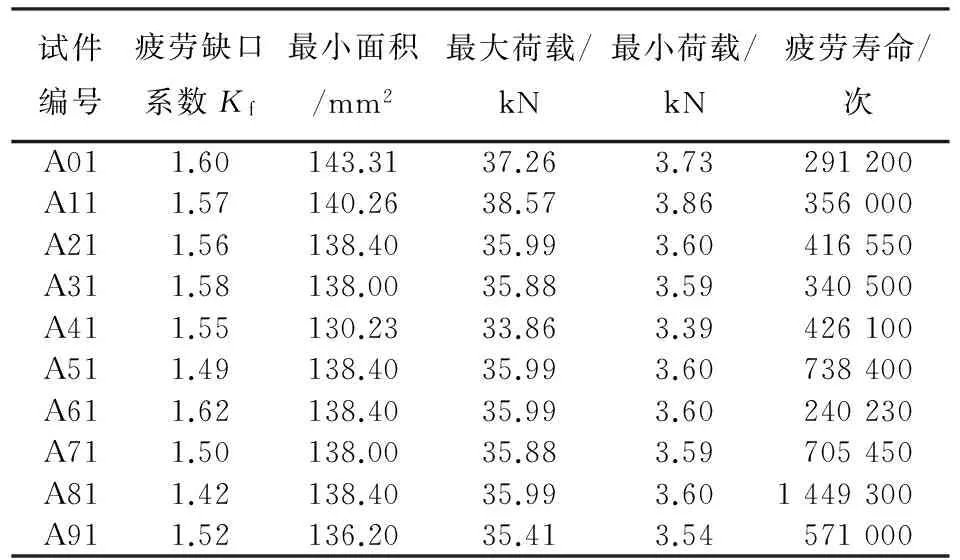
表1 腐蚀钢板疲劳试验结果
3 钢板疲劳缺口系数仿真模拟方法
3.1 疲劳缺口系数计算公式
理论应力集中系数Kt[14]为缺口平面上局部最大弹性应力与名义应力之比.
(4)
Kt可用有限元或光弹法和电阻实验测得,它只与试样几何形状有关,不受材料影响.一般称其为形状系数,代表缺口处应力提高的倍数或程度.理论应力集中系数Kt是以弹性力学理论为基础,假设材料为弹性,而实际材料往往呈现出不同程度的塑性.
迄今为止,有不少具有实际价值的疲劳缺口系数表达式已被提出.工程中常用的有Neuber[15]公式,提出Kf与Kt的关系式为
(5)
式中:ρ为缺口根部半径;ρ′为材料常数,文献[15]认为ρ′是与材料晶粒尺寸有关的常数.文献[16]则提出ρ′为抗拉强度的函数.文献[10]推荐了Neuber-Kuhn公式ρ′的曲线,为Kf计算提供依据.
在已知诸多公式中Peterson[17]公式仍然是工程中比较实用的表达式.
(6)
式中a是与热处理方式有关的常数.
3.2 钢板锈蚀面几何模型重构
利用三维非接触式表面形貌仪测得腐蚀结构钢高精度的三维点云数据,运用Geomagic Studio对点云数据进行后处理、腐蚀形貌特征重建.腐蚀模型需要保留表面特征,处理中保留大部分噪点,过滤掉超过设定阈值的孤立噪声点,手动去除偏离曲面的点.封装后进入多边形阶段,通过细分三角形改善曲面光滑度,检查表面特征符合要求,平面截面去除有缺口的边界部分.最后构造精确曲面布局图,探测轮廓线、曲率线进而构造曲面片,实现数据的分割与曲面重构,定义面板类型构造格栅而获得整齐的网格划分,从而拟合出光顺的NURBS曲面.图4为腐蚀42 d试件腐蚀表面NURBS曲面的重构基本过程.

图4 A31试件腐蚀表面NURBS曲面重构基本过程
重建的CAD曲面模型与原数之间需要进行误差检测,通过实测模型与曲面模型的误差精度分析,适当调整曲面模型,最终控制误差范围.将20个曲面模型原始点云和曲面导入Geomagic Qualify中进行误差比较分析,所有模型标准偏差均在0.03 mm以内,拟合误差非常小,满足精度的要求.
3.3 有限元数值分析
将Geomagic Studio软件中建立的曲面模型导入ANSYS环境中进行有限元仿真分析.应用ANSYS创建三维实体,模拟尺寸截取疲劳试验标准试件标据范围内钢板尺寸,为60 mm×20 mm,实测钢材厚度平均值为7.2 mm,ANSYS在复杂三维模型显示方面有局限性,无法显示Geomagic Studio中建立的腐蚀表面NURBS曲面特征,下图模型为ANSYS建模导入三维设计软件CATIA中显示的实体模型,见图5.
本文研究的三维模型采用20节点solid95实体单元.网格划分越小,划分的曲面网格越接近真实情况,但是受到试验点检测仪器以及软件计算精度的影响,如果划分过细,误差会小于这两者的实际误差,这种情况下再进行细致的划分,对于结果也没有多大意义.所以,通过试算后,确定了本文输入的网格划分长度为0.003,如图6所示.

图5 有限元分析几何模型

图6 网格划分及局部细节
计算模型长边一侧端部施加固端约束,可以简化计算并有利于收敛,在另一侧60 mm端部施加100 MPa面荷载,保证构件表面缺口部分局部最大应力在弹性范围内.计算前,弹性模量E=1.978 25×105MPa,泊松比v=0.3.
图7为腐蚀42 d的模型应力分布图,通过局部放大可以看到明显的点蚀区域.由于圣维南原理的影响,应力最大值没在腐蚀表面,而是在被约束面的角点.由于腐蚀坑的位置、形状、深度都具有随机性,当腐蚀表面形貌较为平坦时,这部分区域应力集中并不明显,当腐蚀表面出现点蚀坑时,表面应力的最大点均在点蚀坑处.因此,应选取坑蚀应力集中系数最大点得到应力集中系数.
图8为应力集中系数-时间分布图.本文模拟的腐蚀钢材共10个模型,从图8可以发现应力集中系数值随着腐蚀时间变长由2.12逐渐减小至1.15,表明钢材由最初点蚀逐渐进入了平均腐蚀阶段,随后在均匀腐蚀的基础上,再发生点蚀,但此时绝对点蚀深度相对于前期点蚀深度较浅,且仅在部分区域小范围内有点蚀现象,因而应力集中系数只是小幅度增加.

图7 三维应力集中系数分布图

图8 应力集中系数-时间分布
3.4 有限元仿真结果与试验结果对比分析
将ANSYS创建的几何模型导入三维模拟软件CATIA中测量应力集中系数最大点的缺口根部半径ρ.Nueber公式中ρ′通过查文献[10]中曲线获得,在钢材极限强度450 MPa时取0.72,Peterson公式中a值取0.40,有限元计算预测疲劳缺口系数与试验值对比分析见表2.
表2 仿真与实测疲劳缺口系数结果对比
Tab.2 Comparison of fatigue notch coefficient of simulation and measured

试件编号缺口半径/mm有限元法KtKf试验值Perterson公式KfNeuber公式KfA00.832.121.601.761.63A10.952.031.571.721.59A22.131.741.561.621.50A33.801.691.581.571.49A41.981.411.551.351.28A5—1.151.49——A6—1.451.62——A72.661.441.501.381.31A84.801.431.421.401.32A93.001.431.521.381.30
分析表2数据,可发现Neuber公式得到的疲劳缺口系数非常接近试验值,Perterson公式在仿真腐蚀表面模拟计算得到的值普遍偏大,较为保守.在应力集中系数相同情况下,这两个公式反映了缺口根部半径对疲劳缺口系数的影响程度,随着缺口根部半径ρ的增大或减小,Neuber公式受ρ变化的影响较小.由于腐蚀表面最大应力处缺口特征的测量结果不易获得,需多次测量求得平均值作为最终缺口根部半径,其精确度对最终结果有一定影响.
从模拟结果可看出试件A0~A3四个模型具有明显点蚀现象,应用Perterson公式和Neuber公式计算得到的疲劳缺口系数与试验值误差均在5%以内,说明仿真模拟疲劳缺口系数值有一定正确性和可行性.进入平均腐蚀阶段后,表面应力集中系数的最大值分布区域广,接近平面,无法获得精确的缺口半径,对于区域均匀腐蚀的构件,缺口半径趋于无穷大,同时疲劳缺口系数也趋于无穷大,公式中对于缺口半径的定义并不适用于均匀腐蚀,Perterson公式和Neuber公式在真实腐蚀中计算疲劳缺口系数具有局限性.因此,利用疲劳缺口系数作为影响实际腐蚀构件疲劳寿命预测时不能直接应用修正S-N曲线,需要先判断腐蚀结构应力最大也就是应力集中系数最大的点位于点蚀部位还是均匀腐蚀区域,Perterson公式和Neuber公式适用于腐蚀试件中最大应力集中系数在点蚀区域的状况.
4 结 论
1)本文将逆向工程的概念引入结构分析中,利用Geomagic Studio仿真拟合出腐蚀结构钢表面特征曲面,使得复杂形貌研究精确化.
2)ANSYS建立了三维仿真模型,与传统试验方法相比,可灵活、高效地估算各种复杂形貌构件的疲劳缺口系数,疲劳缺口系数仿真模拟值与试验值非常接近.说明有限元法仿真模拟对疲劳缺口系数预测的正确性.
3)由于Perterson公式和Neuber公式在真实腐蚀构件复杂形貌的情况下应用具有局限性,因此,在实际腐蚀构件预测疲劳寿命时不能直接应用计算结果,需要先对腐蚀阶段是否为点蚀做出判断.
[1] 金平,杨凯,薛庆増. 腐蚀环境下材料的疲劳缺口系数[J]. 海军航空工程学院学报, 2010,25(5):485-487,492. JING Ping, YANG Kai, XUE Qingzeng. Fatigue notch factor of corrosion material[J]. Journal of Naval Aeronautical and Astronautical University, 2010,25(5):485-487,492.
[2] 夏开全,姚卫星. 疲劳缺口系数评述[J]. 南京航空航天大学学报, 1994,26(5): 676-685. XIA Kaiquan, YAO Weixing. Fatigue notch factor: a review [J]. Journal of Nanjing University of Aeronautics & Astronautics, 1994,26(5): 676-685.
[3] 丁遂栋. 结构钢疲劳缺口系数研究[J]. 机械强度, 2000, 22(3):241-242. DOI:10.16579/j.issn.1001.9669.2000.03.024. DING Suidong. Study on fatigue notch coefficient for structural steel [J]. Journal of Mechanical Strength, 2000, 22(3):241-242. DOI:10.16579/j.issn.1001.9669.2000.03.024.
[4] 雷宏刚,裴艳,刘丽君. 高强度螺栓疲劳缺口系数的有限元分析[J]. 工程力学, 2008,25(增1): 49-53. LEI Honggang, PEI Yan, LIU Lijun. Finite element analysis of fatigue notch factor for high-strength bolts [J]. Engineering Mechanics, 2008,25(S1): 49-53.
[5] CERIT M. Numerical investigation on torsional stress concentration factor at the semi elliptical corrosion pit[J]. Corros Sci, 2013, 67:225-232. DOI:10.1016/j.corsci.2012.10.028.
[6] CERIT M, GENEL K, EKSI S. Numerical investigation on stress concentration of corrosion pit[J]. Engineering Failure Analysis, 2009, 16(7): 2467-2472. DOI:10.1016/j.engfailanal.2009.04.004.
[7] 张明. 基于非接触式扫描的三维轮廓提取及可视化研究[D]. 重庆:重庆大学, 2014. ZHANG Ming. Research on 3D contour extraction and visualization based on non-contact scanning [D]. Chongqing: Chongqing University, 2014.
[8] 刘伟军,孙玉文.逆向工程原理、方法及应用[M].北京:机械工业出版社,2008. LIU Weijun, SUN Yuwen. Principle method and application of reverse engineering [M]. Beijing: Mechanical Industry Press, 2008.
[9] LEE K H, WOO H, SUK T. Data reduction methods for reverse engineering [J]. International Journal of Advanced Manufacturing Technology, 2001, 17(10):735-743. DOI:10.1007/s001700170119. [10]王忠保,方向威. 机械工程材料性能数据手册[M].北京:机械工业出版社,1994:43-50. WANG Zhongbao, FANG Xiangwei. Performance data handbook of mechanical engineering materials [M]. Beijing: Mechanical Industry Press, 1994:43-50.
[11]汪保良. 锈蚀对低碳钢疲劳寿命及裂纹扩展速率影响的试验研究[D].济南:山东大学,2008. WANG Baoliang. Experimental study on fatigue life and crack growth rate of low carbon steel with corrosion [D]. Jinan: Shandong University, 2008.
[12]平安,王德俊.计算疲劳缺口系数的新方法[C]//第5届全国疲劳学术会议论文集.威海:中国航空学会,中国力学学会,中 国机械工程学会,中国金属学会, 1991:354-357. PING An, WANG Dejun. A new method for calculating the fatigue notch factor [C]// Proceedings of the Fifth National Conference on fatigue. Weihai: China Aviation society, China mechanical society, China Mechanical Engineering Society, Chinese society of metals, 1991:354-357.
[13]韦丽金.点蚀疲劳寿命估算的投影面积法[D].南京: 南京航空航天大学,2008. WEI Linjin. Projection area method for fatigue life estimation of pitting corrosion [D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2008.
[14]胡本润,刘建中,陈剑锋. 疲劳缺口系数Kf与应力集中系数Kt之间的关系[J].材料工程,2007(7):70-73. HU Benrun, LIU Jianzhong, CHEN Jianfeng. Relationship between fatigue notch factorKfand stress concentration factorKt[J]. Journal of Materials Engineering, 2007 (7): 70-73.
[15]NEUBER H. Theory of stress concentration for shear strained prismatical bodies with arbitory nonlinear stress-strain law [J]. Journal of Applied Mechanics, ASME, 1961, 28(4):544 -550. DOI:10.1115/1.3641780.
[16]FUCHS H O, STEPHENS R I. Metal fatigue in engineering [M].New York: John Wiley, 1980:45-80.
[17]PETERSON R E. Notch sensitivity [M]. New York: McGraw-Hill, 1959: 290-306.
(编辑 赵丽莹)
Fatigue notch factor of corrosion steel plate considering surface topography
XU Shanhua, QIN Guangchong, JI Lixing, WANG Youde
(School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055,China)
To simulate the complex morphology of steel plate and obtain the fatigue notch factor based on real surface topography, the Q235 steel plate was corroded rapidly by salt spray method, and the corrosion surface was measured by three dimensional measurement. Three-dimensional solid model was established, and the surface stress distribution was analyzed by reverse engineering Geomagic Studio software and numerical analysis software ANSYS. Then the numerical results and experimental results were compared. The results show that the error is small enough, which verifies the feasibility of the modeling methods. Geomagic studio can achieve a rapid 3D visual modeling and simulate the corrosion morphology well, combined with ANSYS, it can estimate the fatigue notch factors of various complex morphology components flexibly and efficiently.
corrosion steel; surface morphology; reverse engineering; numerical analysis; fatigue notch factor
10.11918/j.issn.0367-6234.2016.12.022
2015-03-26
国家自然科学基金(51378417);教育部长江学者和创新团队发展计划项目(IRT13089)
徐善华(1963—),男,教授,博士生导师
秦广冲,qinguangchong@126.com
TU50
A
0367-6234(2016)12-0153-05

