网壳结构钢与混凝土组合节点力学性能试验

郑 亮，邵晓波，刘杰峰，郭紫燕，涂礼松，田子童，宁 蕊，董彦莉

(中北大学 土木工程学科管理部，太原030051)



网壳结构钢与混凝土组合节点力学性能试验

郑 亮，邵晓波，刘杰峰，郭紫燕，涂礼松，田子童，宁 蕊，董彦莉

(中北大学 土木工程学科管理部，太原030051)

为研究钢与混凝土组合的网壳节点在轴压和压弯荷载作用下的力学性能，对10个不同参数的钢与混凝土组合的节点进行试验研究.试验构件主要变化参数包括：内圆钢管的壁厚和半径、外圆钢管的壁厚及矩形钢管与外圆钢管的不同连接方式.试验研究表明：在轴压和压弯荷载作用下节点表现出了与钢管混凝土相似的特点，具有较高的承载力和良好的塑性变形能力；内圆钢管的壁厚和半径对节点承载力影响较大，外圆钢管的壁厚对节点承载力影响较小；连接方式对节点承载力影响较大，圆钢管高于矩形钢管的节点承载力比圆钢管与矩形钢管齐平的承载力至少提高15%；轴压荷载作用下节点的破坏方式可以分为中心压缩和梭形偏转破坏；压弯荷载作用下节点的破坏方式分为节点和钢管屈服破坏.关键词: 钢与混凝土组合；网壳节点；轴压试验；偏压；承载力

网壳节点是网壳结构中最重要的传力构件，节点的承载力对网壳结构的承载力有重要影响，特别是网壳节点处受到拉力、压力、弯矩和剪力的共同作用受力较为复杂.国内外学者对网壳节点的力学性能和极限承载力进行了大量研究，文献[1-7]对螺栓球节点的半刚性性质及其网壳的稳定性能进行了研究，得出半刚性节点的网壳具有很好的承载能力.文献[8]对新型螺栓球节点在轴向拉力作用下进行了试验研究，得到该节点的破坏模式及承载力.文献[9-15]对焊接空心球节点进行了试验研究并提出相关理论公式.现阶段网壳节点都是由钢材制作，节点用钢量占整个网壳结构用钢量的20%～50%，并且制作工艺较为复杂且造价较高.特别是在矩形钢管网壳结构中，网壳节点通常采用相贯节点，为了保证相贯节点有足够的刚度和强度通常要增加矩形钢管的壁厚，这样将导致整个网壳结构用钢量增加.因此，为降低网壳结构的用钢量和造价，同时结合并利用钢管混凝土承载力高、刚度大和变形小的特点，提出一种钢与混凝土组合的网壳节点，如采用该节点可以减小矩形钢管的壁厚，降低网壳结构的整体用钢量，同时该节点与焊接空心球和螺栓球节点的制作工艺相比，该节点的制作工艺较简单，造价也低，从而降低矩形钢管网壳结构的整体造价.目前网壳结构中关于钢与混凝土组合的网壳节点力学性能还未见报道，为了进一步了解该网壳节点力学性能，有必要对钢与混凝土组合的节点在轴压和压弯荷载作用下的力学性能进行研究.钢与混凝土组合的网壳节点见图1.

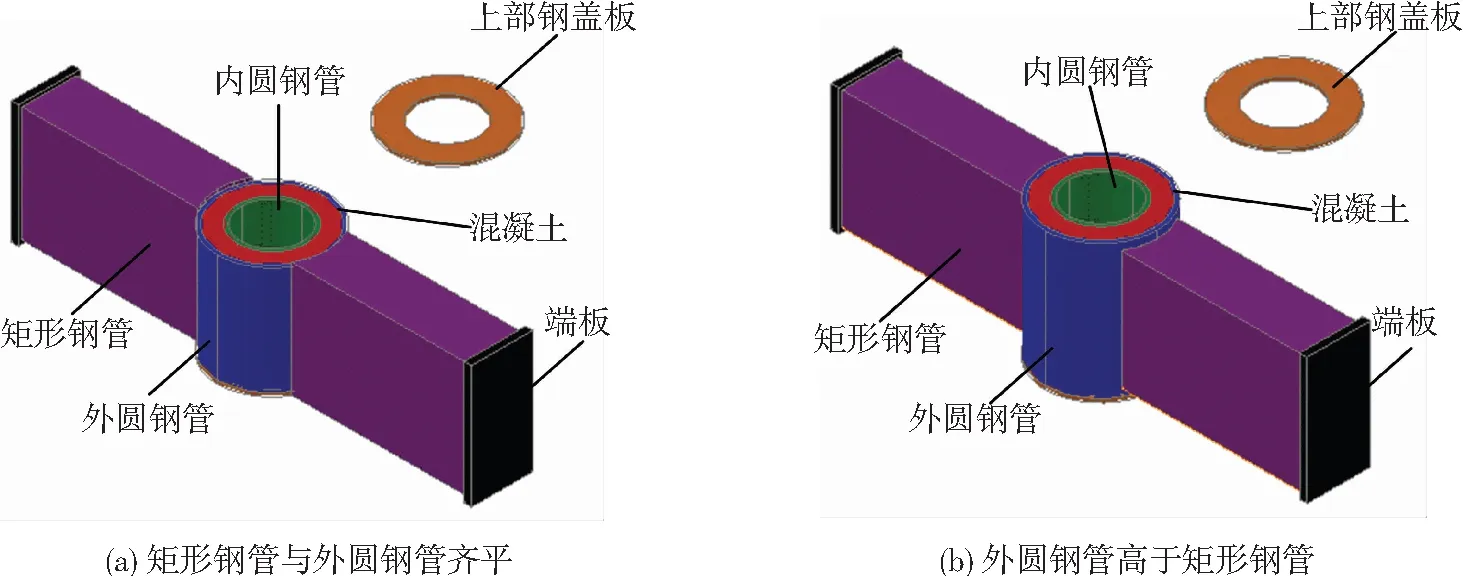
图1 钢与混凝土组合的网壳节点

1 试验概况

1.1 试件设计

在试件设计时，矩形钢管的选择主要考虑两个方面：1)组合节点破坏前矩形钢管不能出现强度破坏.如果组合节点破坏前钢管强度破坏，将无法研究组合节点的破坏机理和极限承载力.故矩形钢管的壁厚取节点内外圆钢管的最大壁厚，同时矩形钢管的钢材采用Q345B；2)矩形钢管不能太长.如果太长会出现矩形钢管受压失稳破坏，同时也会造成定位和焊接拼装的偏差，引起较大的二次弯矩.因此，取矩形钢管长度为200 mm，高度150 mm，宽度85 mm，钢管壁厚5 mm.对于压弯荷载作用下的构件而言，为使组合节点不受加载面的约束和影响，取矩形钢管的长度为600 mm，同时加载端采用专用的加载刀口铰.

试验共设计了10个钢与混凝土组合的网壳节点试验构件，试验构件的参数变化包括：内圆钢管壁厚和半径、外圆钢管壁厚及矩形钢管与外圆钢管的连接方式.组合节点各试验构件的具体设计参数列于表1.构件1～5进行轴压试验，构件6～10进行压弯试验.

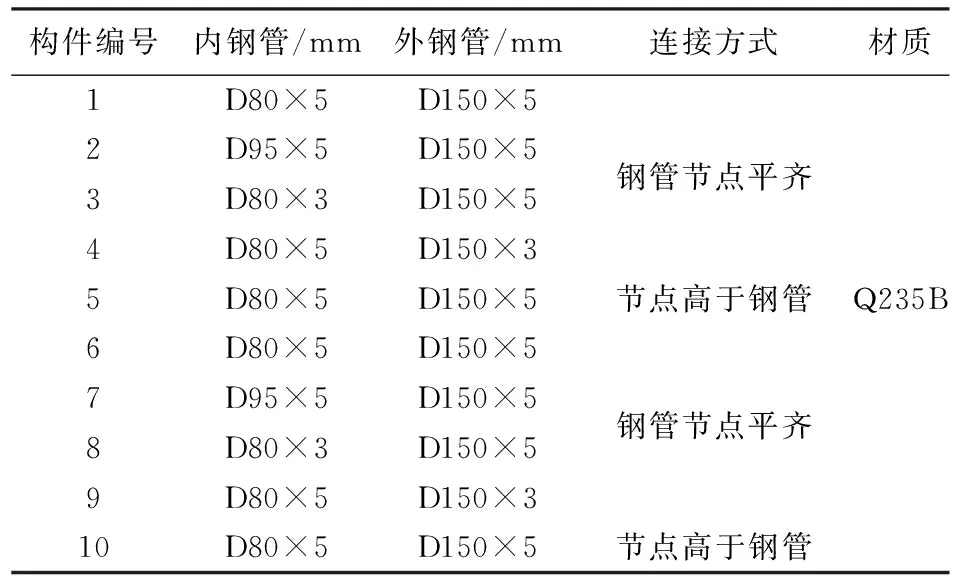
表1 试验构件具体设计参数

注：D代表钢管直径.

通过材性试验可知，内外圆钢管的力学性能指标见表2，试验中所采用的混凝土力学性能指标见表3.

表2 钢材屈服强度和弹性模量

表3 混凝土强度和弹性模量

1.2 试验加载方案及装置

钢与混凝土组合的网壳节点试验采用2 000 kN压力机，通过压力机对组合节点试件进行单调加载直至试验构件达到极限承载力而破坏.加载装置见图2.

图2 钢与混凝土组合节点加载装置

在压弯构件的端部焊接端板和竖板，竖板是为了保证压弯试验中刀口铰可以发生自由转动而不会在压力作用下发生相对于端板的移动，见图3(a).为使压弯构件不受加载端约束而自由转动，对刀口铰的上部构件进行切角1处理.对刀口铰的下部构件进行切角2处理的目的是使刀口铰的下部构件和竖板能够接触紧密且加载偏心距不受端板和竖板焊缝的影响.压弯构件加载刀口铰见图3.

图3 加载刀口铰装置

为顺利完成试验加载过程，将加载过程分为两个阶段：预加载和正式加载.正式加载采用分级加载的方式.由于试验没有相关文献作为参考，为得到较为精确的试验数据，在试验构件的弹性阶段内，每级加载值约为极限荷载的10%，分级逐步加载到构件达到屈服强度；节点达到屈服强度之后，每级荷载值进一步缩小.当加荷载到试验试件极限荷载值的90%以后，应缓慢连续加载，直到试件达到极限承载力而破坏.同时，为了使试件在荷载作用下的变形得到充分发展且达到稳定，每级荷载加载完毕后，每级加载间停留时间不得少于2 min.

1.3 测量方案设计

在钢与混凝土组合节点试验中，根据试验目的量测内容可以分为轴压和压弯荷载、试验构件整体变形、节点表面应变以及局部变形.

轴压荷载和压弯荷载作用下，矩形钢管的应变计沿矩形钢管对称轴纵向布置在4个表面，测量矩形钢管与组合节点处矩形钢管的应变.组合节点钢盖板上的应变计沿着对称轴横向和纵向均匀布置，测量钢盖板上应变的分布.在外圆钢管表面矩形钢管两侧沿着钢管中部环向均匀布置3个应变计，测量圆钢管对混凝土的约束能力；同时在矩形钢管两侧圆钢管表面中部沿着纵向轴线对称位置布置应变计，测量外圆钢管纵向的应变，应变计的布置如图4所示，括号内的数值是另一侧应变计的编号.

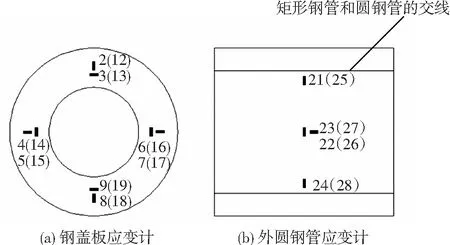
图4 钢与混凝土组合节点应变计布置

2 试验结果及对比分析

2.1 试验现象

通过试验可知，10个钢与混凝土组合节点的变形过程与钢管混凝土相类似，大致可以分为3个阶段：弹性阶段、弹塑性阶段和破坏阶段.轴压和压弯荷载作用下试验构件的荷载-位移曲线见图5、6.

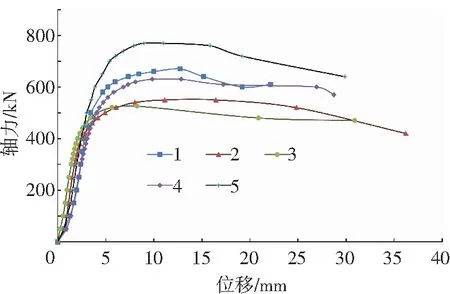
图5 轴压荷载作用下钢与混凝土组合节点荷载-位移曲线

Fig.5 Load displacement curves of steel and concrete composite joints under axial compressive load

图6 压弯荷载作用下钢与混凝土组合节点荷载-位移曲线

Fig.6 Load displacement curves of steel and concrete composite joints under bending load

在轴压荷载作用下荷载小于屈服荷载之前为弹性阶段，在弹性阶段试件的外观基本无变化，荷载和位移曲线呈线性的关系；当荷载大于屈服荷载后构件进入在弹塑性阶段，该阶段试验构件的内外圆管出现明显被压扁的变形趋势，荷载与位移曲线呈现明显的非线性；当荷载增加到极限荷载后构件进入破坏阶段，可以观察到试验构件内外圆管已经被压扁，端部的钢盖板变形断裂，同时钢盖板与内外钢管的焊缝开裂，开裂处可以看到内部混凝土被压碎，此时试验构件位移增加较快，荷载随着位移增加逐步下降.试验构件的荷载-位移曲线见图5，图中的数字代表节点试验构件的编号.

在压弯荷载作用下，在弹性阶段试验构件的外观基本无变化；在弹塑性阶段压弯构件受压侧有压扁的趋势，受拉侧也有变形，但受拉侧和受压侧变形不明显；在破坏阶段压弯构件受拉侧内外圆钢管和钢盖板在拉应力作用下拉成椭圆形，受压侧内外圆钢管和钢盖板在压应力作用下被压扁，同时受压侧可以听到混凝土被压碎的声音.与轴压荷载作用下试件变形不同，压弯荷载作用下内外圆钢管和钢盖板之间的焊缝并没有开裂.压弯荷载作用下各试验构件的荷载-位移曲线见图6.

图6中构件10的荷载-位移曲线在达到极限承载力后，承载力曲线的下降幅度比其他压弯构件大，这是由于组合节点未达到极限承载力而与组合节点连接处的矩形钢管受压侧已经屈曲，矩形钢管屈曲后由于内部没有混凝土的支撑作用，承载力会快速下降.

2.2 破坏形态

通过5个钢与混凝土组合节点轴压试验，可将轴压试件的破坏形态分为两类：一类是内外圆钢管被压成椭圆形的中心压缩破坏，此类破坏上下矩形钢管没有明显的相对位移；另一类是内外圆钢管被压成梭形的偏转破坏，此类破坏上下矩形钢管有明显的相对位移.两种破坏方式中构件的钢盖板都受压断裂，钢盖板与内外圆钢管的焊缝开裂，开裂处可见混凝土被压碎.轴压试件两种典型的破坏形态见图7.

图7 轴压荷载下钢与混凝土组合节点典型破坏形态

Fig.7 Typical failure modes of steel and concrete composite joints under axial compressive load

通过5个钢与混凝土组合节点压弯试验，可将压弯试件的破坏形态分为两类：一类是受压侧内外圆钢管被压成椭圆形，受拉侧内外圆钢管被拉成椭圆形，但受拉侧变形较小；另一类为与组合节点连接处的矩形钢管受压侧发生局部屈曲，受拉侧和受压侧内外圆钢管变形较小.连接方式为圆钢管高于矩形钢管的组合节点发生矩形钢管受压屈曲的破坏形态.两种破坏形态中构件的钢盖板都没被压裂，钢盖板与内外圆钢管的焊缝也没有开裂.压弯试件两种典型的破坏形态见图8.

图8 压弯荷载下钢与混凝土组合节点典型破坏形态

Fig.8 Typical failure modes of steel and concrete composite joints under bending load

2.3 应变分析

各个试验构件在测点2、9、3、8处只有部分屈服，其余都不屈服.其它测点在节点破坏时全部达到屈服强度.以轴压构件1、5和压弯构件6、10为例说明矩形钢管与外圆钢管两种连接方式节点的应变分布及破坏机理的不同.通过应变分析，钢盖板上测点5、7和外圆钢管上测点23、27是应变最大处，由于构件是对称的，因此只列出构件1、5和构件6、10在测点5、22、26及27处的应变变化见图9、10.测点5测量钢盖板上的应变，测点27测量外圆钢管的环向应变，测点22和26测量外圆钢管的轴向应变.

以轴压构件1和5为例说明在不同连接方式条件下外圆钢管及钢盖板表面的应变变化.从图9、10可见，在相同的荷载条件下，构件5外圆钢管表面的环向应变和轴向应变比构件1相应位置处的应变小.同时，构件5钢盖板上的应变也比构件1相应位置处的应变小.因此，构件1外圆钢管在环向和轴向双向应力作用下先于构件5达到屈服强度，而且构件1钢盖板应力也会首先屈服.

综上所述分析，在相同荷载条件下，构件5外圆钢管和钢盖板对内部混凝土的约束能力强于构件1，而组合节点的承载力取决于钢管对内部混凝土的约束能力，因此，构件5的承载力高于构件1.

压弯构件以构件6和10为例说明在不同连接方式条件下外圆钢管及钢盖板表面的应变变化，从图9、10可见，压弯构件外圆钢管及钢盖板表面应变的发展和轴向受压构件相类似.构件6外圆钢管在环向和轴向双向应力作用下先于构件10达到屈服强度，而且构件6钢盖板应力也会首先屈服.因此，构件10的承载力高于构件6.

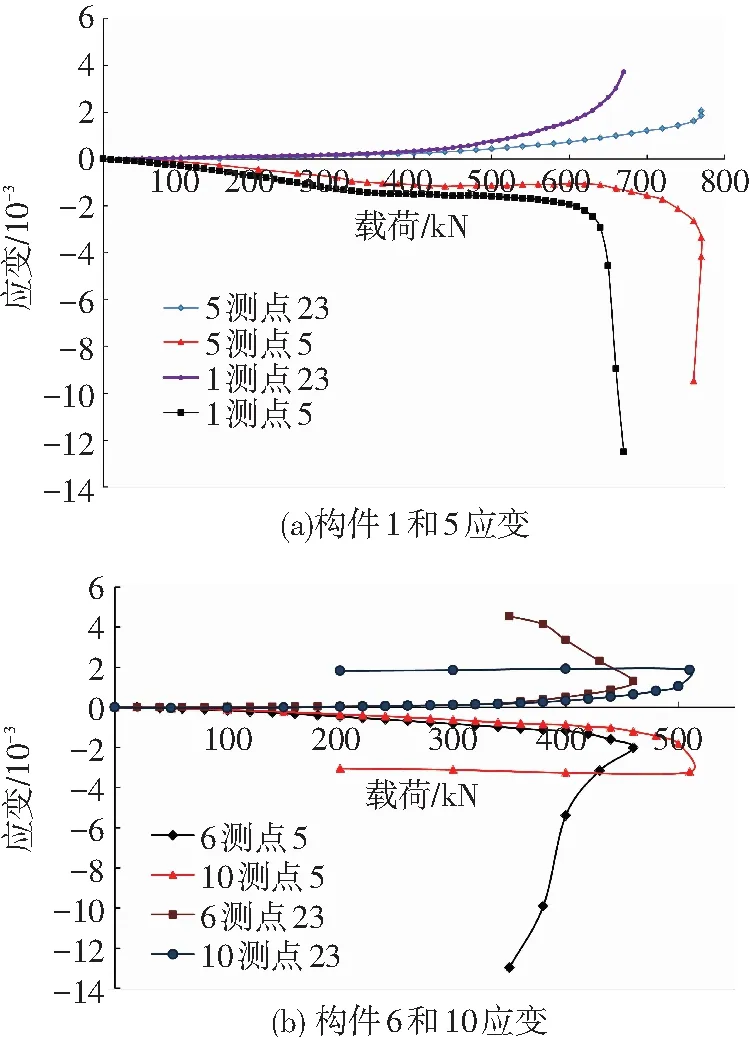
图9 试验构件钢盖板和外圆钢管应变

Fig.9 Strain of test components steel cover plate and outer circle steel tube

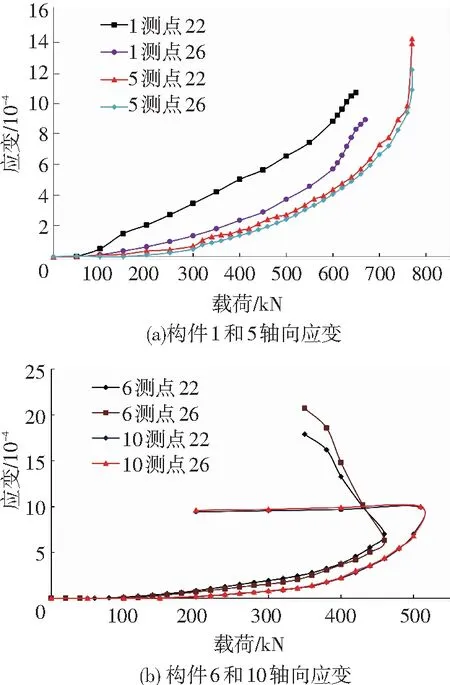
图10 试验构件轴向应变

从上述分析可知，组合节点破坏是由外圆钢管在环向和轴向双向应力作用下屈曲失去对内部混凝土的约束作用，随后钢盖板也达到屈服并受压开裂，开裂处内部混凝土被压碎，从而使组合节点达到极限承载力而破坏.

在图9(b)、10(b)中，构件10的应变曲线中有一段近似于水平的线段，这是由于组合节点破坏以前矩形钢管受压区已经发生局部屈曲，从而使得组合节点的承载力无法继续增加，因此，组合节点外圆钢管的轴向和环向应变无法继续增加而呈现出一条近似的水平直线段.

2.4 试验结果对比

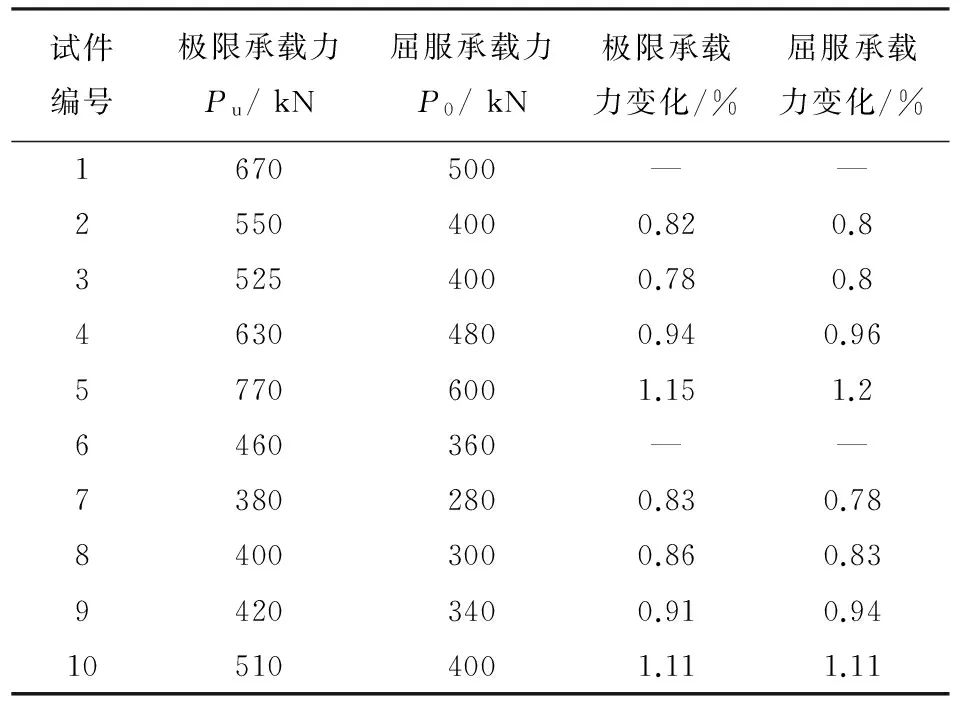
通过轴压和压弯荷载作用下的试验研究，将钢与混凝土组合节点的极限承载力和屈服承载力试验结果列于表4.其中轴压构件1～5极限承载力和屈服承载力的变化是构件2～5的极限承载力和屈服承载力与构件1相应承载力的比值；压弯构件6～10极限承载力和屈服承载力的变化是构件7～10的极限承载力和屈服承载力与构件6相应承载力的比值.

表4 钢与混凝土组合节点承载力试验结果

Tab.4 Test results of bearing capacity of steel and concrete composite joints

试件编号极限承载力Pu/kN屈服承载力P0/kN极限承载力变化/%屈服承载力变化/%1670500——25504000.820.835254000.780.846304800.940.9657706001.151.26460360——73802800.830.7884003000.860.8394203400.910.94105104001.111.11

从表4可知，轴压构件2的极限承载力Pu和屈服承载力P0比构件1分别降低18%和20%；压弯构件7的极限承载力Pu和屈服承载力P0比构件6分别降低17%和22%.这是由于构件2和7的内圆钢管直径分别比构件1和6增大15 mm，增大内钢管直径将减小填充混凝土的厚度，因此，改变混凝土填充厚度将显著的降低组合节点的承载力.

构件3的外圆钢管壁厚比构件1减小2 mm，而构件3的极限承载力Pu和屈服承载力P0比构件1分别降低22%和20%；构件4的内圆钢管壁厚比构件1减小2 mm，而构件4的极限承载力Pu和屈服承载力P0比构件1分别降低6%和4%.构件8的外圆钢管壁厚比构件6减小2 mm，而构件8的极限承载力Pu和屈服承载力P0比构件6分别降低14%和 17%；构件9的内圆钢管壁厚比构件6减小2 mm，而构件9的极限承载力Pu和屈服承载力P0比构件6分别降低9%和6%.从上述分析可知，对轴压和压弯构件而言，改变外圆钢管的壁厚对组合节点极限承载力和屈服承载力的影响更为显著.

从外圆钢管和钢盖板的应变分析可知，连接方式为圆钢管高于矩形钢管的组合节点外圆钢管和钢盖板对内部混凝土的约束能力较强.因此，构件5和10的承载力分别比构件1和6有较大幅度的提高.

综合上所述分析，在轴压和压弯荷载作用下，混凝土填充厚度和外圆钢管壁厚对组合节点的极限承载力和屈服承载力的影响较为显著，内圆钢管壁厚对组合节点的极限承载力和屈服承载力的影响较小.

3 结 论

1)在轴压和压弯荷载作用下，组合节点表现出了与钢管混凝土相似的特性，具有较高的承载力和良好的塑性变形能力.

2)通过试验研究，内外圆钢管之间混凝土填充厚度和外圆钢管壁厚对组合节点的承载力的影响较为显著，内圆钢管壁厚对组合节点承载力的影响较小.

3)节点圆钢管高于矩形钢管的组合节点对内部混凝土约束较强，该种组合节点的承载力较高.

[1] 马会环,范峰,柯嘉阳.网架网壳结构半刚性节点试验研究[J].建筑结构学报,2010,31(11):65-71.DOI: 10.14006/j.jzjgxb.2010.11.009. MA Huihuan, FAN Feng, KE Jiayang. Experimental research on semi-rigid joints used in grid structures and reticulated domes[J].Journal of Building Structures,2010,31(11):65-71.DOI: 10.14006/j.jzjgxb.2010.11.009.

[2] 范峰,马会环,沈世钊.半刚性螺栓球节点单层K8型网壳弹塑性稳定分析[J].土木工程学报,2009,42(2):45-52. DOI:10.15951/j.tmgcxb.2009.02.015. FAN Feng, MA Huihuan, SHEN Shizhao. Elasto-plastic stability analysis of K8 single-layer reticulated shells with bolt-ball joint system[J].China Civil Engineering Journal,2009,42(2):45-52.DOI:10.15951/j.tmgcxb. 2009.02.015.

[3] FAN Feng,WANG Minling,CAO Zhenggang.Seismic behaviour and seismic design of single-layer reticulated shells with semi-rigid joint system[J].Advances in Structural Engineering,2012,15(10):1829-1841.DOI:10. 1260/1369-4332.15.10.1829.

[4] MA Huihuan, FAN Feng,SHEN Shizhao.Numerical parametric investigation of single-layer latticed domes with semirigid joints[J].Journal of the International Association for Shell and Spatial Structures,2008,49(2):99-110． [5] 曹正罡,范峰,马会环.螺栓球节点试验及在单层网壳结构中的应用性[J].哈尔滨工业大学学报,2010,42(4): 525-530. CAO Zhenggang, FAN Feng, MA Huihuan. Experiment of bolt-ball joint and its application in single-layer reticulated shells[J].Journal of Harbin Institute of Technology,2010, 42(4): 525-530.

[6] FAN Feng,MA Huihuan,CHEN Gengbo.Experimental study of semi-rigid joint systems subjected to bending with and without axial force[J].Journal of Constructional Steel Research,2012,68(3):126-137.DOI:10.1016/j.jcsr. 2011.07.020.

[7] KATO S,MUTOH I,SHOMURA M.Collapse of semi-rigidly jointed reticulated domes with initial geometric imperfections[J].Journal of Constructional Steel Research,1998,48(4):145-168.DOI:10.1016/S0143-974X(98) 00199-0.

[8] WANG Xiaodun,WENG Kai,LIU Hongbo.Experimental study on the mechanical property of visual bolt-ball joint system[J].Advances in Structural Engineering,2013,16(10):1749-1761.DOI:10.1260/1369-4332.16.10. 1749.

[9] 董石麟,邢丽,傅学怡.矩形钢管焊接空心球节点承载能力的简化理论解与实用计算方法研究[J].土木工程学报,2006,39(6):12-18. DOI:10.15951/j.tmgcxb.2006.06.003. DONG Shilin, XING Li, Fu Xueyi. Simplified theoretical solution and practical calculation method for welded hollow spherical joints of rectangular hollow section members[J].China Civil Engineering Journal,2006,39(6): 12-18.DOI:10.15951/j.tmgcxb.2006.06.003.

[10]曾毅恒,朱丹,赵基达.北京A380大跨机库节点承载力试验研究[J].土木工程学报,2008,41(2):29-34.DOI: 10.15951/j.tmgcxb.2008.02.008. ZENG Yiheng, ZHU Dan, ZHAO Jida. Experimental study on the ultimate bearing capacity of the joints in Beijing A380 hangar[J].China Civil Engineering Journal,2008,41(2):29-34.DOI:10.15951/j.tmgcxb.2008. 02.008.

[11]EMMETT A S,THOMAS M M.Behavior of extended end-plate moment connections subject to cyclic loading[J].Journal of Structural Engineering,ASCE,2002,128(4):501-508.DOI:10.1061/(ASCE)0733-9445 (2002)128:4(501).

[12]秦力一,许德刚,周爱民.空间网架焊接空心球节点承载力研究[J].郑州大学学报,2006,27(3):25-29. QIN Liyi, XU Degang, ZHOU Aimin. Research on bearing capacity of welded hollow spherical joint of space truss[J].Journal of Zhengzhou University,2006,27(3):25-29.

[13]纪晗,熊世树,黄丽婷.大型焊接空心球节点的多轴加载有限元分析与足尺试验[J].工程力学,2010,27(4): 173-178. JI Han, XIONG Shishu, HUANG Liting. Finite element analysis and full-scale experimental study on large spherical joint in multi-axial loading[J].Engineering Mechanics,2010,27(4):173-178.

[14]袁行飞,彭张立,董石麟.平面内三向轴压和弯矩共同作用下焊接空心球节点承载力[J].浙江大学学报,2007,41(9):1436-1442. YUAN Xingfei, PENG Zhangli, DONG Shilin. Load-carrying capacity of welded hollow spherical joints subject to combined planar tri-directional axial force and bending moment[J].Journal of Zhejiang University,2007, 41(9):1436-1442.

[15]董石麟,唐海军,赵阳.轴力和弯矩共同作用下焊接空心球节点承载力研究与实用计算方法[J].土木工程学报,2005,38(1):21-30.DOI:10.15951/j.tmgcxb.2005.01.003. DONG Shilin, TANG Haijun, ZHAO Yang. Load-carrying capacity and practical calculation method for welded hollow spherical joints subject to combined axial force and bending moment[J].China Civil Engineering Journal, 2005,38(1):21-30. DOI:10.15951/j.tmgcxb.2005.01.003.

(编辑 赵丽莹)

Mechanical properties on steel and concrete composite joints in reticulated domes

ZHENG Liang, SHAO Xiaobo, LIU Jiefeng, GUO Ziyan, TU Lisong, TIAN Zitong, NING Rui, DONG Yanli

(Department of Civil Engineering, North University of China, Taiyuan 030051，China)

To study the mechanical properties of steel and concrete composite joints under axial compression loads, ten steel and concrete composite joints with different parameters were tested. The main parameter changes of test member include: an inner pipe wall thickness and the radius of the circle, the wall thickness of the outer pipe and the connections between rectangular steel tube and the outer tubes. The experimental results show that steel and concrete composite joints have much in common with steel and concrete, i.e., it has high capacity and good plastic deformation capacity under axial compression loads; the wall thickness and radius of inner pipe is larger than the wall thickness of the outer pipe on the bearing capacity. Connections have greater influence on the joints bearing capacity than others. The bearing capacity of round steel tube is higher than rectangular one and it will be raised at least 15% than the same capacity of round steel tubes and rectangular ones. Under axial compression loads, the failure mode of joints can be divided into central compression failure and spindle deflection failure. Under eccentric loading, the failure mode of joints is divided into joints failure and steel yield damage of pipe.

steel and concrete composite; joints of reticulated domes; axial compression test; eccentric loading; bearing capacity

10.11918/j.issn.0367-6234.2016.12.011

2015-12-01

国家自然科学基金青年科学基金(51208473)

郑 亮(1977—)，男，博士，讲师

郑 亮，zl_5403@126.com

TU398

A

0367-6234(2016)12-0083-06