基于改进蚁群算法的移动机器人三维路径规划

朱颢东， 孙 振， 吴 迪

(郑州轻工业学院 计算机与通信工程学院， 郑州 450002)



基于改进蚁群算法的移动机器人三维路径规划

朱颢东*， 孙 振， 吴 迪

(郑州轻工业学院 计算机与通信工程学院， 郑州 450002)

三维路径规划是移动机器人研究领域的核心内容之一.传统的蚁群算法应用于三维路径规划时，存在收敛速度慢，容易陷入局部最优解等问题.针对这些问题，论文对路径节点的选取方法、信息素的更新方法、启发函数的设计进行了改进，从而避免了算法陷入局部最优解，加快了算法的收敛速度.仿真实验表明改进算法在不同复杂程度的环境中都可以得到最优路径，且路径规划结果较好，这表明了算法有良好的寻优能力.

蚁群算法； 路径规划； 三维空间

路径规划技术是移动机器人关键技术之一和重要的研究内容，也是衡量移动机器人智能化水平的标准之一.机器人路径规划是指在环境已知或者部分未知的情况下，有效避开障碍物的前提下寻找一条从起始点到目的点的最优路径[1].目前，国内外有许多专家学者利用不同的算法对移动机器人路径规划进行了研究，这些算法有A*算法[2]、遗传算法[3]、神经网络算法[4]、人工势场算法[5]等，但是这些算法以往主要是应用在二维环境中来解决路径规划的问题.由于三维环境更加的贴近人们的生产生活，在三维环境中研究机器人路径规划意义重大，近年来，三维空间的路径规划成为了国内外研究的热点之一.但是，由于在三维空间中路径规划问题具有占用存储空间大、计算复杂等难题，导致有些算法很难广泛应用到三维路径规划.对于三维路径规划问题，目前采用的方法主要有神经网络算法、人工势场算法、遗传算法等，这些算法已经应用到三维路径规划问题，但是存在着较大的局限性.文献[6]提出了基于模拟退火神经网络算法移动机器人三维路径规划方法，在障碍物的拐角处用到了平滑策略，有效提高了规划路径的质量.文献[7]提出了一种基于人工势场法的无人飞行器三维路径规划方法，使用一个八叉树的结构表示可移动的对象，飞行器从起始位置通过平移和旋转来搜索相邻区域，直到找到目标地为止.文献[8]提出了基于遗传算法对一组移动机器人三维路径规划方法，首先通过对机器人的初始位置，目标地为止，障碍物等信息建模，然后通过调用地图中的信息来搜寻路径.文献[9]通过对人工势场法的栅格运行费用评估模型和栅格的斥力函数进行改进，有效的解决了三维路径规划中环境适应性和全局性差的问题，提供了一种新的路径规划研究思路.A*算法能够应用到简单环境中的三维路径问题，但是随着环境复杂程度的增加，A*算法将很难满足时间和空间的要求，规划的路径不理想.人工势场法虽然相对应用比较简单，但是难以克服局部极小值和目标不可达问题，不利于推广应用.遗传算法由于进化代数众多，会占用大量的空间，在简单的环境中应用还可以，在复杂的环境中很难规划一条理想的路径.

蚁群算法是1992年由Marco Dorigo在其博士论文中提出，通过观察蚂蚁寻找食物源时发现路径的行为而获得启发.蚁群算法是一种模拟进化算法，具有自组织性、较强的鲁棒性、分布式计算、寻优能力强和易于和其他算法相结合等优点，非常适合应用到移动机器人三维路径规划问题[10].因此，论文提出利用改进蚁群算法对移动机器人三维路径规划，论文首先对移动机器人的环境进行建模，然后设计了启发函数，改进了信息素的更新方式，通过在Matlab软件中仿真实验，表明了该改进算法的有效性和可行性.

1问题描述及环境建模

路径规划中的重要环节之一是环境建模.环境建模是根据机器人周围的环境，通过提取和分析，将现实世界中真实的信息用抽象的方式进行表达，转换成机器人可以理解的信息.通过良好的环境建模，可以提高路径规划的效率.本文主要采用空间等分网格方法对环境进行抽象建模，建模方法如图1所示.

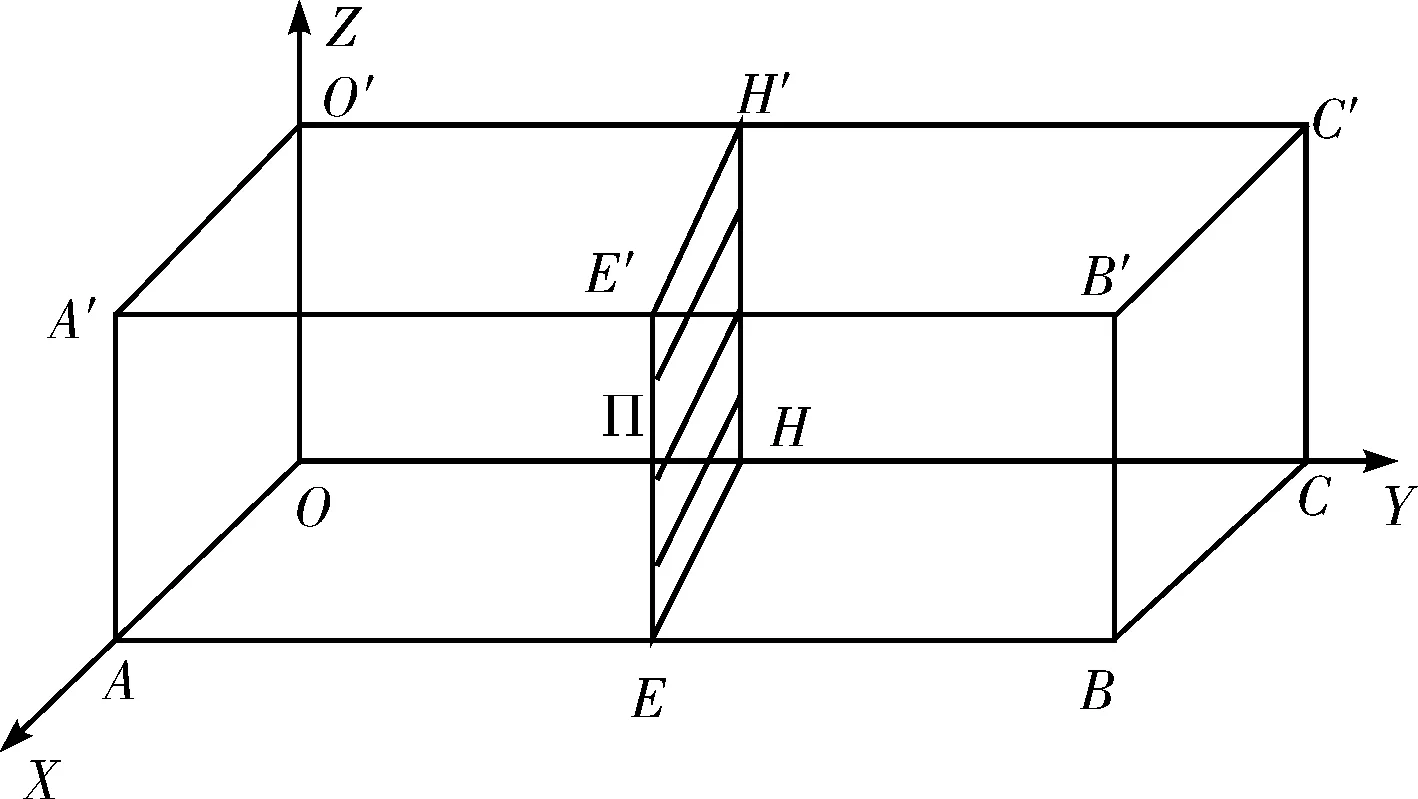
图1 规划空间的划分Fig.1 The division of planning space

首先构造一个规划空间OABC-O’A’B’C’，将三维地图中左下角的O 为顶点，在O点建立三维坐标系，其中，x 轴沿着经度增加的方向，y 轴沿着维度增加的方向，z 轴为垂直于海面的方向.坐标系中以O点为顶点，沿着x轴的方向取三维地图的最大长度OA，沿着y轴的方向取三地图的最大长度OC，沿着z轴的方向取三维地图的最大长度OO’，构建三维地图的立方体区域OABC-O’A’B’C’.三维路径空间建立起来以后，对规划空间进行划分，采用等分空间的方法从三维空间中抽取三维路径所需要的网格点.首先沿着边OC对规划空间OABC-O’A’B’C’进行n等分，将会得到n+1个平面Πj(j=0，1，2，…，n) ，然后对任一平面Πj沿着OA边进行m 等分，再沿着OO'边进行m等分，并且求解出相关的交点[1].平面划分图如图2所示.

将规划空间OABC-O’A’B’C’离散化为一些点，这些点的集合设为P*，空间中任意一点都有两个坐标与其对应，即p1(i，j，k)(其中{i=0，1，2，…，m}、{j=0，1，2，…，n}、{k=0，1，2，…，m})和p2(xi，yi，zi)，其中，i 、j 、k 分别是该点所对应的划分序号.

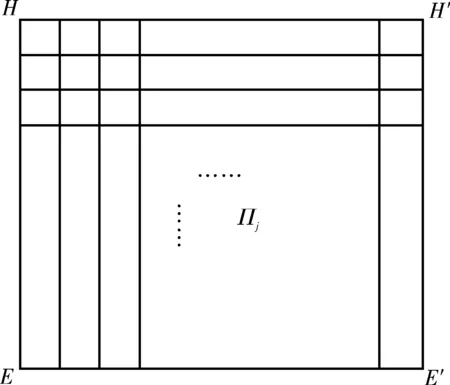
图2 任意平面Πj的划分Fig.2 The division of an arbitrary plane Πj

2本文所采用的三维路径规划

2.1有效路径生成方法

路径规划就是寻找从起始点到目的点的一系列的点，这些点与相邻点之间的连线不和环境中障碍物相交，找到最短的点的序列即是机器人的路径.机器人从起始点O 出发，首先到达平面Π1上某一点p1(i1，j1，k1)(i1，k1∈(0，1，2，…，m)j1∈(0，1，2，…，n))，然后再到达平面Π2上面某一个点p2(i2，j2，k2) ，再然后到平面Πn-1的某一点上pn-1(in-1，jn-1，kn-1)，直到搜索到目标点T为止，连接pn-1(in-1，jn-1，kn-1)和目标点T，这样就构成了一条从起始点O 到目标点T的路径，即O→p1(i1，j1，k1)→p2(i2，j2，k2)→…→ pn-1(in-1，jn-1，kn-1)→ T.当机器人所处复杂的环境中，起始点O和目标点T之间不可避免的会存在障碍物，当存在障碍物时，这条路径是无效的，所以，引进如下定义.

定义1对平面Πj+1上任意一点pi+1(ii+1，ji+1，ki+1)，如果线段pipi+1不与任何障碍物相交，则把pi+1存入一个列表，本文把这个列表定义为allowed(i，j，k)表，计算出当前节点pi所有可行节点，存入allowed(i，j，k)表中.

定义2本文中用欧氏距离来表示任意两点pi、pi+1的距离，这样就把两点间的最优路径问题转化为求解两点间最短距离的问题，任意两点间的距离可用公式(1)表示：

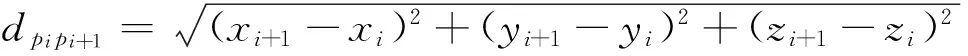
(1)

蚁群算法只需要搜索这些三维路径上的离散的点，最终链接到起始点和目的点，既可以得到最优三维路径.

2.2信息素的表示

大多情况下会把相邻节点间的路径作为信息素的载体，由于三维空间求解路径规划环境模型中节点较多，若将各个节点间的路径作为载体，算法的空间复杂度将会很高，所以这种方法不太适合.每一个平面Πj中有m2个节点，相邻两个平面ΠjΠj+1的连线将会有m4种情况，随着划分间隔距离的减小，m 会逐渐变大，连线的情况也会随之变多，算法的空间复杂度也会变大.所以，论文中采用节点表示法，利用各个离散的节点来存储信息素，每一个点对应一个信息素值，信息素值的大小代表着吸引程度的大小，这样相邻的两个平面ΠjΠj+1上只有2m2种连线情况，有效降低空间的复杂度.

2.3转移规则的设计

伪随机比例规则可以利用节点之间距离的启发信息和节点上存储的信息素的先验知识对节点进行搜索.论文中引入伪随机比例规则，增加了蚁群算法搜索的多样性.

蚂蚁从当前节点选择下一个节点的概率跟启发式函数有较大的关系，所以启发式函数影响着概率公式.我们设一组有m只蚂蚁，最初蚂蚁被放置在起始位置，蚂蚁k按照公式(2)进行下一步位置选择.

(2)

其中，J是根据公式(3)给出的概率分布产生的一个随机变量，q 是[0，1] 之间的一个常数，q0在[0，1]区间且符合正态分布的随机数.

平面Πi上的任意一点Pi(ii，ji，ki)上的蚂蚁，选择平面Πi+1上任意一点Pi+1(ii+1，ji+1，ki+1) 的概率为如公式(3)所示.

(3)

其中，τi+1是平面Πi+1上点Pi+1(ii+1，ji+1，ki+1)上储存的信息量， F 为启发函数，启发函数是保证蚁群算法在合理的时间内搜索到全局最优解的关键点.

2.4启发函数的设计

启发式函数的设计是三维空间路径规划中的重要环节，一个合适的启发函数可以使得算法快速的规划出一条效果理想的三维路径.函数中需要尽可能多的考虑的各项因素，以此来构建路径优化的标准.文献[1]中把障碍物约束条件和路径最短作为两个评价函数，障碍物约束条件可用公式(4)表示.

(4)

当前节点和任意相邻可行节点间的欧式距离为两点间最短路径距离，则路径最短的启发函数为

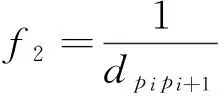
(5)

本文中的启发函数基于考虑障碍物约束条件、路径最短和可行节点距目标点的距离3个因素，加入可行节点到目标点的距离这个因素，可以使得搜索更具有方向性，加快算法的搜索速度，任意当前节点的下一个可行节点距离目标点的距离的启发函数为

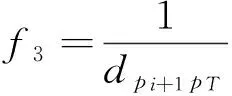
(6)

把下一个任意节点到目标点的距离引入到启发函数中，如公式(7)所示，

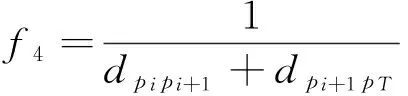
(7)

综上，论文中设计的启发函数为

F=f1*f4.

(8)

2.5信息素的更新规则

基于蚁群算法的三维路径规划是把整个搜索空间离散化为一系列的三维离散点，这些离散点是蚂蚁需要搜索的节点，把信息素存储在离散的点中，每一个离散的点都有一个信息素的值，该点信息素的大小代表着对蚂蚁的吸引程度，各点的信息度值在蚂蚁经过之后更新.

基本的蚁群算法存在着容易陷入局部最优解和收敛速度慢的问题，当还未出现最优的路径时，蚂蚁可能会不断增加当前路径节点上的信息素浓度，使得后续的蚂蚁越来越多的选择这条路径，随着时间的增加，很容易使得算法停滞.论文采用局部信息素更新和全局信息素更新相结合的方式进行信息素更新.局部信息素更新在蚂蚁路径搜索路径的过程中进行，蚂蚁选择一个节点后，利用公式(9)对节点上的信息素进行更新.

τijk=(1-ξ)τijk+ξτ0，

(9)

其中，ξ 是一个参数，取值范围在(0，1)之间，τ0是各个可行解点间的初始信息素量.

全局信息素更新是在本代的蚂蚁找到一条完整的路径之后进行信息素的更新.找出当代蚂蚁中搜索到的最短路径，只更新最短路径各个节点的信息素值.更新规则为

τijk=(1-ρ)τijk+ρΔτijk,

(10)

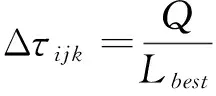
(11)

其中，ρ 是信息素的挥发速率，Lbest表示当代蚂蚁中最优路径长度，Q是信息素浓度常数.

3算法流程

本文算法流程如下.

Step1：初始化参数，根据机器人所在的环境进行抽象环境建模.确定起始点、目的点的位置和搜索方向，将所有的蚂蚁置于起始点.

Step2：根据公式(8)计算各个可行节点的启发函数，根据各个节点的启发函数来选择下一个可行节点.

Step3：当蚂蚁k移动到下一节点，根据公式(9)对当前节点进行局部信息素的更新.

Step4：判断是否所有的蚂蚁找到一条路径，若找到，根据公式(10)进行全局信息素的更新，如若否，返回步骤2，继续寻优.

Step5：判断是否达到最大的迭代次数，如果否，转向步骤2继续寻优，如果是，输出当前群体中最短的路径，即最优的三维路径.

4实验仿真

实验一：不同复杂环境中的仿真实验

(1)随机生成一类地图，设置路径的起始点和目标点.种群规模为：20，最大迭代次数为200.改进蚁群算法路径规划结果如图3所示.

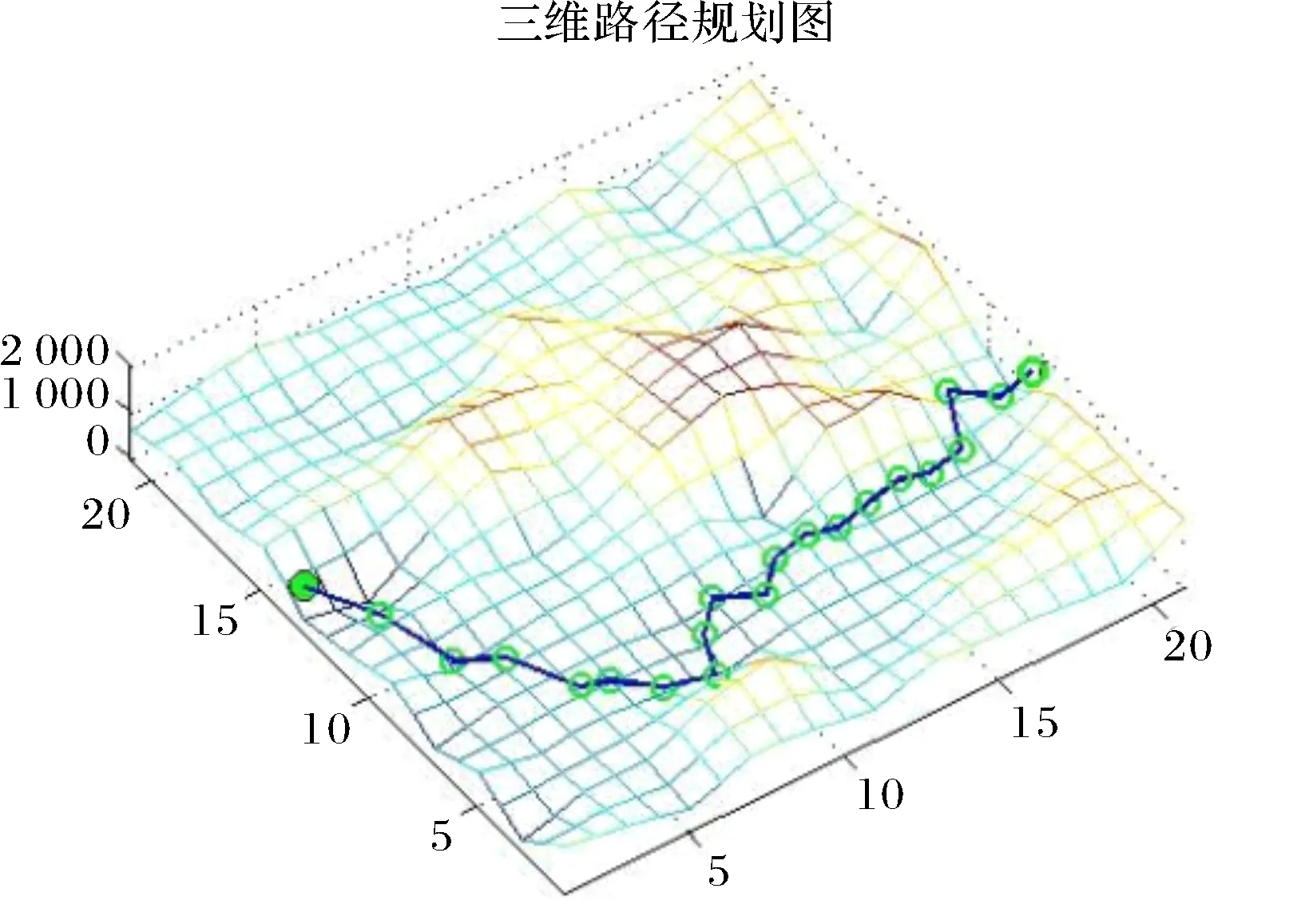
图3 改进蚁群算法的路径规划结果Fig.3 The results of path planning based on improved ant colony algorithm

(2)随机生成一类地图，设置路径的起始点和目标点，种群规模为20，最大迭代次数为200.改进蚁群算法路径规划结果如图4所示.

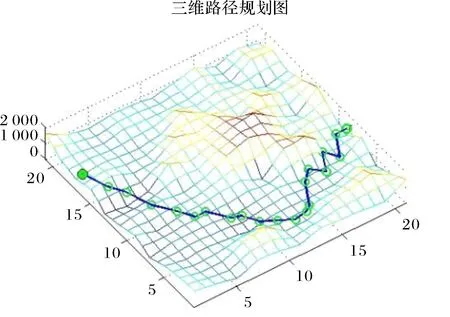
图4 改进蚁群算法的路径规划结果Fig.4 The results of path planning based on improved ant colony algorithm

通过在不同复杂的环境中设置不同的起始点和目标点，论文提出的改进蚁群算法都可以快速搜索出较优的路径结果，证明了改进算法的有效性和可行性.

实验二：和基本蚁群算法的对比实验

(1)随机生成的一类三维地图1，在相同的地图环境中分别对基本蚁群算法和本文改进蚁群算法进行仿真，设置相同的起始点和种群个数，实验结果如图5和图6所示.

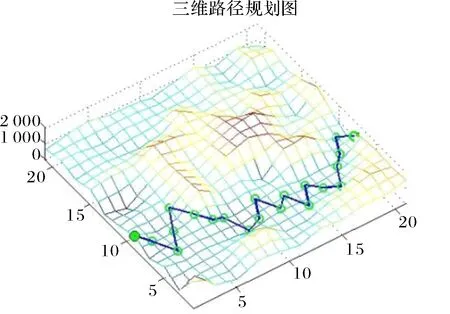
图5 基本蚁群算法的路径规划结果Fig.5 The results of path planning based on basic ant colony algorithm

图6 改进蚁群算法的路径规划结果Fig.6 The results of path planning based on improved ant colony algorithm

(2)随机生成的一类三维地图2，在相同的地图环境中分别对基本蚁群算法和本文改进蚁群算法进行仿真，设置相同的起始点和种群个数，实验结果图7和图8所示.

图7 基本蚁群算法的路径规划结果Fig.7 The results of path planning based on basic ant colony algorithm

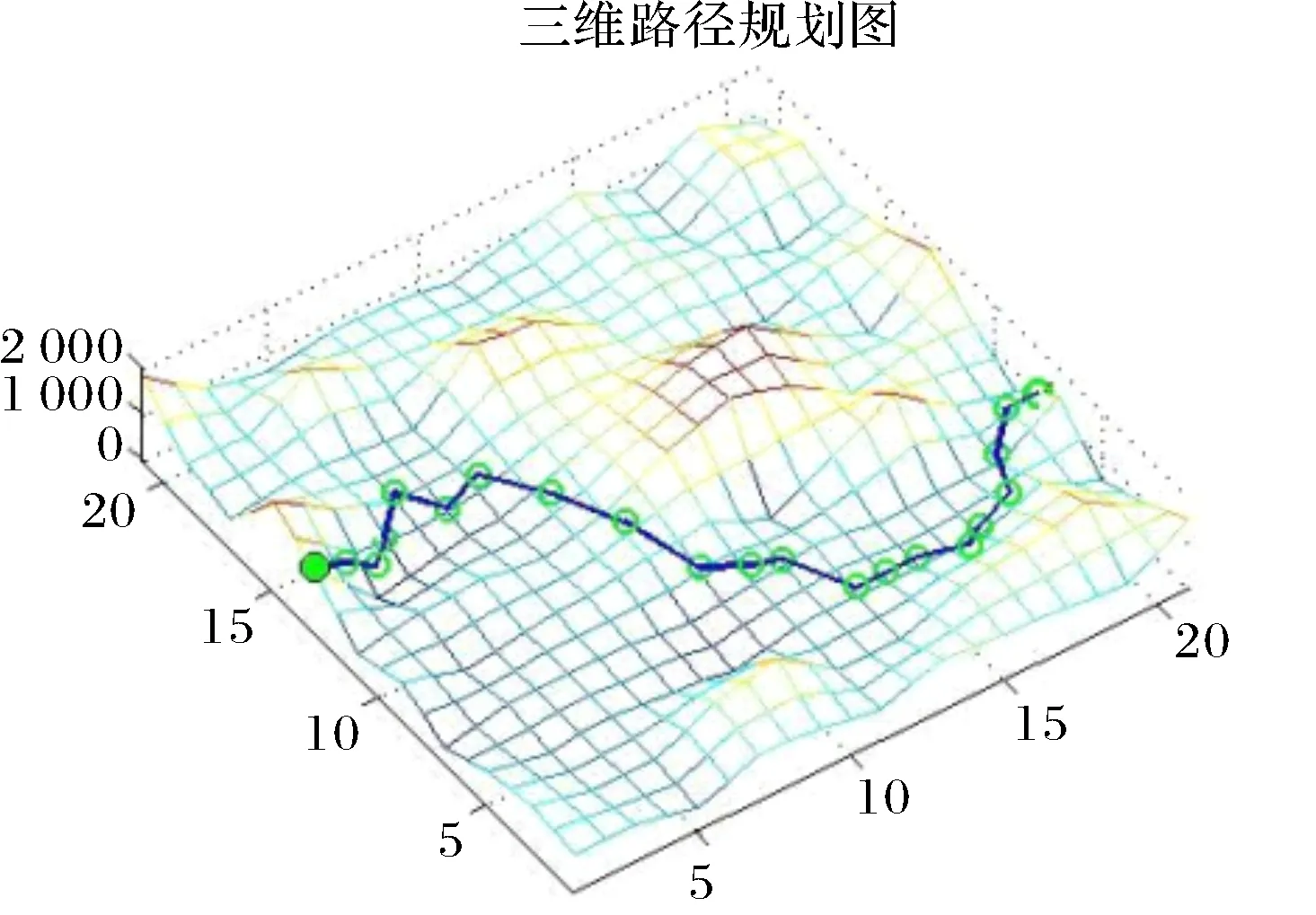
图8 改进蚁群算法的路径规划结果Fig.8 The results of path planning based on improved ant colony algorithm

(3)随机生成的一类三维地图3，在相同的地图环境中分别对基本蚁群算法和本文改进蚁群算法进行仿真，设置相同的起始点和种群个数，实验结果图9和图10所示.

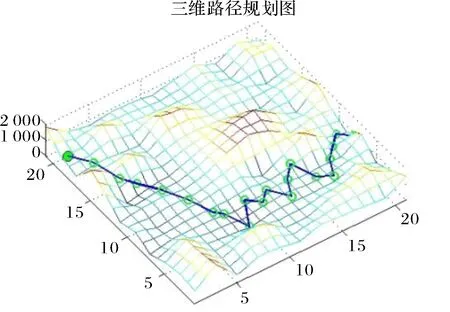
图9 基本蚁群算法的路径规划结果Fig.9 The results of path planning based on basic ant colony algorithm

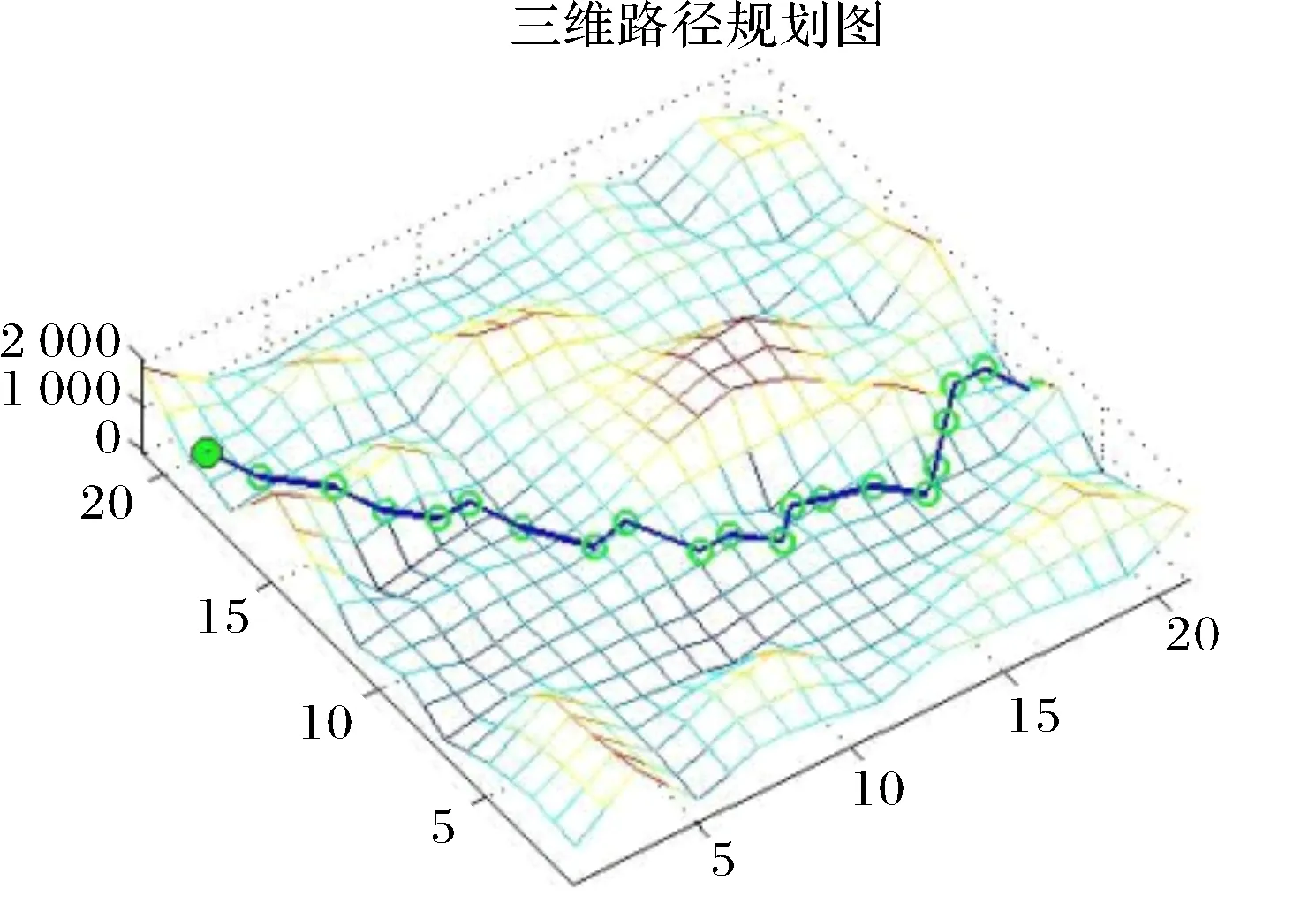
图10 改进蚁群算法的路径规划结果Fig.10 The results of path planning based on improved ant colony algorithm

在3类不同复杂程度的环境中，论文中改进蚁群算法和基本蚁群算法的路径规划结果如表1所示.

表1 路径规划结果比较

由于论文在启发函数的设计中加入可行节点到目标点的距离这个因素，可以使得搜索更具有方向性，加快算法的搜索速度；论文改进了信息素的更新方式，有效的克服了算法容易陷入局部最优解，收敛速度慢等问题.通过对比仿真实验可以看出，论文改进蚁群算法三维路径规划结果均优于基本蚁群算法，证明了改进蚁群算法具有一定的优越性.

5结束语

本文针对传统蚁群算法在路径规划时容易陷入局部最优解、收敛速度慢等问题，并且针对三维路径的复杂性和多样性，提出了一种基于改进蚁群的三维路径规划方法.通过对环境的抽象建模、路径节点的选取、启发函数的设计等一系列的改进，为移动机器人在三维环境中规划提供了一种参考方法.通过在不同三维环境中仿真实验，改进算法均能得到较优路径规划结果，表明了改进算法的有效性和可行性.通过在不同复杂程度的环境中和基本蚁群算法进行对比实验，改进蚁群算法的路径规划结果均优于基本蚁群算法的路径规划结果，表明了改进蚁群算法具有一定的优越性.

[1] 胡 荟， 蔡秀珊. 机器人三维路径规划问题的一种改进蚁群算法[J].计算机工程与科学， 2012， 34(11):153-157．

[2] 王殿君. 基于改进A*算法的室内移动机器人路径规划[J].清华大学学报， 2012， 52(8):1085-1089．

[3] 段俊花， 李孝安. 基于改进遗传算法的机器人路径规划[J]. 微电子学与计算机， 2005， 22(1):70-72．

[4] 陈志华， 谢存禧， 曾德怀. 基于神经网络的移动机器人路径规划算法的仿真[J].华南理工大学学报(自然科学版)， 2003， 31(6):56-59．

[5] YIN L， YIN Y Y， LIN C J. A new potential field method for mobile robot path planning in the dynamic environments[J]. Asian Journal of Control， 2009， 11(2): 214-225.

[6] KROUMOV V， YU J L， SHIBAYAMA K. 3D path planning for mobile robots using simulated annealing neural network[J]. International Journal of Innovative Computing， Information and Control， 2010， 6(7): 2885-2899．

[7] KITAMURA Y， TANAKA T， KISHINO F， et al. 3-d path planning in a dynamic environment using an octree and an artificial potential field[C]//Proc 1995 IEEE Int Conference on Intelligent Robots and Systems. IEEE: Piscataway， N J，USA, 1995：474-481．

[8] ZEIN-SABATTO S， RAMAKRISHNAN R. Multiple path planning for a group of mobile robots in a 3D environment using genetic algorithms[C]//Southeast Con， 2002， Proceedings IEEE. IEEE：Piscataway， N J，USA， 2002: 359-363．

[9] 梁家海. 机器人在已知三维自然环境中的路径规划算法[J].计算机工程与设计， 2012， 33(6):2451-2454.

[10] 胡小兵， 黄席樾. 基于蚁群算法的三维空间机器人路径规划[J].重庆大学学报(自然科学版)， 2004， 27(8):132-135．

Path planning for mobile robot in 3D space based on improved ant colony algorithm

ZHU Haodong, SUN Zhen, WU Di

(School of Computer and Communication Engineering， Zhengzhou University of Light Industry， Zhengzhou 450002)

Path planning for mobile robot in 3D Space is one of the core contents in robotics research field in recent years. When the traditional ant colony algorithm was used in path planning for mobile robot in 3D Space, it is easy to fall into local optimum and has a slow convergence speed. In order to overcome the problems, this paper improved the method for choosing the path points, the adaptive heuristic function and the way to update pheromone, which avoids the algorithm falling into local optimal optimum and accelerates the convergence speed. The simulation results show that the improved algorithm is able to obtain the optimal path in the environments of different complexity levels and has better results of path planning which indicates that the improved algorithm possess good optimization ability.

ant colony algorithm; path planning; 3D space

2016-04-22.

河南省高等学校青年骨干教师资助计划项目(2014GGJS-084); 河南省科技攻关项目(152102210149); 郑州轻工业学院校级青年骨干教师培养对象资助计划项目(XGGJS02);郑州轻工业学院博士科研基金资助项目(2010BSJJ038); 郑州轻工业学院研究生科技创新基金资助项目.

1000-1190(2016)06-0812-06

TP242.6

A

*E-mail: zhuhaodong80@163.com.