基于统一强度理论的隧洞弹塑性应力解析

谷拴成，黄荣宾，苏培莉，丁 潇，2，李 昂

(1.西安科技大学 建筑与土木工程学院，陕西 西安 710054；2.西安工业大学 建筑工程学院，陕西 西安 710021)



基于统一强度理论的隧洞弹塑性应力解析

谷拴成1，黄荣宾1，苏培莉1，丁 潇1，2，李 昂1

(1.西安科技大学 建筑与土木工程学院，陕西 西安 710054；2.西安工业大学 建筑工程学院，陕西 西安 710021)

基于统一强度理论对第一主应力为径向应力及环向应力2种情况进行弹塑性应力分析，推导得出了围岩应力及塑性区半径计算公式。隧洞围岩有完全弹性状态、最大主应力为径向应力的弹塑性状态及最大主应力为环向应力的弹塑性状态3种状态，隧洞弹塑性分析时，首先判断围岩所处状态，进而选择正确的公式进行计算。分析结果表明中间主应力有利于围岩充分发挥其强度潜能，从而提高隧洞围岩稳定性，而且中间主应力系数越小，围岩稳定状态对中间应力敏感度越高；当洞内压力小于第二临界应力时，增大洞内压力有利于提高围岩稳定性，而当洞内压力大于第二临界应力时，则围岩稳定性随洞内压力增大而降低。

统一强度理论；隧洞围岩；芬纳公式；中间主应力；弹塑性分析

0 引 言

通过对地下隧洞工程进行弹塑性分析，能够确定隧洞应力分布、围岩位移及围岩塑性区范围，进而为确定合理支护强度及隧洞安全评价提供依据[1-2]。目前工程中通常采用Mohr-Coulomb强度准则进行弹塑性分析，据此推导得出的Fenner公式[3]、修正的Fenner公式及Kastner公式[4-5]在隧洞工程中得到广泛应用。试验证实中间主应力作用能够使围岩强度增大30%[6]，但是应用Mohr-Coulomb强度准则进行围岩弹塑性分析时，将处于三轴应力状态的围岩视为平面应变问题而不能合理考虑中间主应力的影响，从而导致分析结果偏于保守[7]。

统一强度理论以正交八面体及其二分之一与四分之一单元体为统一的物理力学模型，建立了统一强度理论表达式以及一系列典型的计算准则。该理论不仅合理考虑了中间主应力的影响，而且能够退化为Mohr-Coulomb强度准则、Mises强度准则、Tresca强度准则、双剪强度准则及介于Mohr-Coulomb与双剪强度准则之间的各种角隅模型，在不同的工程领域都得到了广泛应用[8]。胡小荣等[9]应用统一强度理论对岩石在三轴压缩载荷下的强度特性进行了理论分析，并将分析结果分别与实验结果和Mohr-Coulomb强度理论作了对比，研究表明统一强度理论能较全面地反映岩石的各种强度特征。王继秀等[10]考虑井筒周围岩石的渗流作用和孔隙水压力的基础上，基于统一强度理对井筒周围岩石进行了弹塑性分析，并给出了井筒周围岩石的应力分布表达式和保持井壁稳定的弹性极限荷载及塑性极限荷载的统一解析式。张常光等[11]采用统一强度理论和弹脆塑性软化模型，推导衬砌和围岩弹塑性应力统一解，在此基础上得出统一强度理论参数、软化特性参数对衬砌和围岩切向应力的影响规律。曾开华等[12]基于统一强度理论和非关联线性流动法则，考虑塑性区的真实弹性应变，推导了深埋圆形隧洞弹塑性位移统一解。

以上研究就应用统一强度理论进行隧洞弹塑性应力分析取得了大量富有意义的结论，但是由于隧洞所处的地应力条件，支护强度，隧洞状态的不同，第一主应力选取有所不同，而现有研究成果未对此加以区分。笔者基于统一强度理论，分别对第一主应力为径向应力与环向应力条件下的隧洞应力进行分析，推导得出相应的塑性区宽度计算公式，并明确不同计算公式的适用条件，同时分析不同参数条件下的围岩应力状态及塑性区宽度的变化规律。

1 计算模型

假定圆形隧洞半径为r0，受到地应力为P，内压力为Pi，塑性区半径为r0.在对隧洞进行弹塑性应力分析时，按照平面应变问题求解，力学模型的基本假设如下[13]：①隧洞断面等效为圆形，长度无限；②原岩应力P为静水压力，即侧压力系数为1；③围岩均质、各向同性、不可压缩材料，计算过程中不计体力影响。

由于隧洞开挖扰动、支护作用及后期运营期间的应力再调整等因素的影响，第一主应力存在径向应力及环向应力2种情况，不同情况下的围岩弹塑性应力分布规律是不同的，在应用统一强度理论进行隧洞弹塑性应力分析时便分情况进行研究。

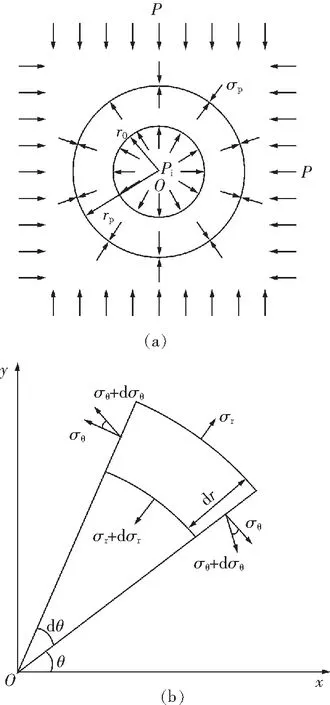
图1 力学计算模型Fig.1 Mechanical analysis model(a)隧洞受力分布 (b)极坐标系中应力分量

2 弹塑性应力分析

2.1 径向应力为第一主应力

在隧洞开挖过程或者内压力相对于地应力处于较小水平时，应力重分布有可能引起围岩在一定范围内出现塑性破坏。分析过程中以受拉为正，受压为负，则此时有σθ<σz<σr<0，即第一主应力应为径向应力。

对于平面应变问题，可假设中间主应力

(1)

其中m为中间主应力系数，0

根据统一强度理论表达式，

(2)

式中 c，φ分别为围岩粘聚力与内摩擦角；b为中间主应力影响参数，表征中间主切应力以及相应面上的正应力对材料破坏影响程度的系数，取值范围为0≤b≤1.

围岩塑性区内假定m=1，由此隧洞围岩统一强度理论为式(2)。图1所示力学计算模型为轴对称平面应变问题，根据弹性力学相关理论，当rp≤r<∞时，弹性应力分布形式为[15]

(3)

轴对称平面应变力学模型的平衡方程式为

(4)

联立式(1)(2b)可得

(5)

联立式(4)及(5)可得

(6)

解得

(7)

式中C为待定系数。

根据边界条件(σr)r=r0=-Pi可得塑性区应力分布为

(8)

(9)

由计算模型可有边界及弹塑性接触面条件如下

(10)

根据(10)可建立方程组，解得

(11)

当b=0时，公式(2)所示的统一强度理论退化为Mohr-Coulomb强度准则，此时式(11)中第三方程式变为

(12)

上式为Fenner公式，即当b=0时，式(11)退化为Fenner公式[16]。

2.2 环向应力为第一主应力

当内水压力很大或支护压力太大时，洞周岩体也可能出现屈服区。由于径向压应力较大，环向压应力较小，甚至成为拉应力，所以第一主应力应为σθ，即σ1=σθ，σ3=σr，同时中间主应力依然为式(1)所示。而围岩屈服准则表达式变为

(13)

联立式(1)(13)可得

(14)

从而有

(15)

解得

(16)

式中D为待定系数。

根据边界条件(σr)r=r0=-Pi可得塑性区应力分布为

(17)

式中

(18)

由边界条件(10)可解得

(19)

当b=0时，公式(2)所示的统一强度理论退化为Mohr-Coulomb强度准则，此时式(19)中第三方程式变为

(20)

上式即为Mohr-Coulomb强度准则条件下，环向应力为第一主应力时的塑性区半径公式。

2.3 公式适用条件

式(11)及式(19)别为最大主应力为径向应力及环向应力条件下，应用统一强度理论推导得出的塑性区半径求解公式。在工程实际中，处于施工期的隧洞，或者内压力较小情况下，最大主应力一般为径向应力，此时应利用式(11)进行隧洞弹塑性应力分析；而处于运行期的水工隧洞或者内压力过大时，最大主应力则转换为环向应力，则应该利用式(19)进行分析。

由上述分析发现，在地应力场作用下，隧洞围岩有3种状态：弹性状态、最大主应力为径向应力条件下的弹塑性状态及最大主应力为环向应力条件下的弹塑性状态。在进行隧洞弹塑性分析前，应首先判断围岩在当前应力场条件下是否出现塑性破坏，然后确定最大主应力方向，进而选择正确的计算公式进行隧洞应力分析。

若隧洞围岩出现塑性区，则应满足

(21)

引入临界应力σp，即当Pi=σp时，rp/r0=1，此时围岩将要出现塑性破坏。分析式(11)及式(19)可知，第一临界应力

(22)

第二临界应力

(23)

由此可以得出应用公式(11)及(19)进行隧洞弹塑性应力分析的适用条件：

1)当Pi<σp1时，围岩部分区域处于塑性状态，且第一主应力为径向应力，此时应用公式(11)进行隧洞弹塑性分析；

2)当σp1≤Pi≤σp2时，围岩完全处于弹性状态，可用弹性力学中轴对称平面应变相关理论进行隧洞应力分析；

3)当σp2

3 算例分析

针对不同的隧洞受力状态，应采取对应的计算公式进行弹塑性分析，而非不加区别的进行分析。同时由于统一强度理论考虑了中间主应力的影响，使得计算结果与Mohr-Coulomb强度准则有所区别。以下通过算例对文中理论进行分析，以验证理论的正确性，同时分析相关参数的影响规律。

圆形隧洞半径r0=8.5m，埋深为180m，原岩应力P=3.55MPa；围岩的粘聚力c=0.2MPa；内摩擦角φ=30°，内压力Pi=0.3MPa；中间主应力系数b=0.25.为进一步研究各参数对隧洞围岩应力分布的影响特点，分别采用单因素影响分析法及多因素影响分析法，得出仅特定因素变化条件下的应力分布变化规律。

在进行分析时，首先利用式(11)计算得出塑性区半径，并根据式(8)及式(3)分别计算出塑性区及弹性区应力分布曲线，图2及图3即显示的是中间主应力系数b分别取0,0.25，0.5，0.75及1.0时环向应力及径向应力分布规律。通过分析，不同情况下围岩塑性区第一主应力都为径向应力，即此时满足Pi<σp1.从图中可以看出，在塑性区范围内，环向应力以较快速率增大至最大值，且随着b值的增大，塑性区内应力随径向坐标变化速率也有增大趋势；同时塑性区内同一位置的径向压应力及环向压应力均有增大趋势，而在弹性区内同一位置的环向压应力及径向压应力随b的增大均有减小趋势；随着b值的增大塑性区范围明显减小，同时弹塑性界面环向压应力由5.49MPa增大至6.63MPa，而径向压应力则由1.60MPa减小至0.48MPa，即弹塑性界面最大剪应力由1.95MPa增大至3.07MPa，说明围岩可以在较大剪应力下仍保持稳定而不发生塑性破坏。

图2 不同b值下环向应力曲线Fig.2 Circumferential stress curves under different b values

图3 不同b值下径向应力曲线Fig.3 Radial stress curves under different b values

图4显示的是中间主应力系数b取不同值条件下围岩塑性区半径rp的变化规律。随着b值由0增大至1.0过程中，塑性区半径rp由14.76m减小至8.70m，b继续增大则围岩由弹塑性状态转为完全弹性状态；同时塑性区半径变化速率由17.81m/L减小至1.78m/L.上述分析说明中间主切应力以及相应面上的正应力有利于围岩保持稳定性，而且中间主应力系数b越小，围岩稳定性状态对中间应力越敏感。

图4 不同b值下塑性区半径变化曲线Fig.4 Curves of plastic zone radius under different b values

图5显示的是b取值不同条件下临界应力σp1及σp2的变化曲线。随着b值由0增大至1.0过程中，第一临界应力σp1由1.60MPa减小至0.43MPa；第二临界应力σp2由5.50MPa增大至6.67MPa，即临界应力差值由3.90MPa增大至6.24MPa.上述分析说明，中间主应力系数b取值越大，围岩越容易由处于最大主应力为径向应力的弹塑性状态进入完全弹性状态，且处于该弹性状态的围岩厚度越大，即b值增大有助于提高隧洞围岩稳定性。

图5 不同b值下临界应力变化曲线Fig.5 Curves of critical stress change under different b values

图6显示的是隧洞内压Pi取不同值条件下塑性区半径变化曲线。利用式(22)及(23)计算确定第一临界应力σp1=1.26MPa，第二临界应力σp2=5.84MPa.当Pi<1.26MPa时，由于隧洞开挖引起地应力释放而造成围岩处于弹塑性状态，且此时最大主应力为径向应力，因此应通过公式(11)计算围岩塑性区半径，随着Pi由0增大至σp1，塑性区半径由20.16m减小至8.50m；当1.26MPa≤Pi≤5.84MPa时，围岩处于完全弹性状态，此时可应用弹性理论进行隧洞应力分析；当Pi>5.84MPa时，由于隧洞内压力过大围岩再次出现塑性破坏且此时最大主应力为环向应力，因此应通过公式(19)计算围岩塑性区半径。利用Fenner公式进行分析时，第一临界应力值为1.68MPa，较式(22)计算结果增大了0.42MPa，且相同隧洞内压力条件下塑性区半径较大，同时没有第二临界应力值，即表示无论隧洞内压力增大至何值，围岩都不会出现塑性破坏，显然该结论是不合理的。

图6 不同隧洞内压Pi下塑性区半径变化曲线Fig.6 Radius change curve of plastic zone under different tunnel pressure Pi

4 结 论

1)基于统一强度理论对隧洞进行弹塑性应力分析，推导得出了第一主应力分别为径向应力与环向应力条件下的隧洞应力解及相应的塑性区半径计算公式。当b=0且仅考虑径向应力为第一主应力时，则文中理论退化为基于Mohr-Coulomb强度理论，而塑性区半径公式退化为Fenner公式；

2)Pi<σp1时围岩部分区域处于塑性状态，且第一主应力为径向应力；σp1≤Pi≤σp2时围岩完全处于弹性状态；σp2

3)随着中间主应力影响系数b增大，弹塑性界面最大主应力、最大剪应力均有增大趋势而塑性区半径有减小趋势；同时围岩越易由处于最大主应力为径向应力的弹塑性状态进入完全弹性状态，且处于该弹性状态的围岩厚度越大。上述分析说明中间主应力有利于围岩充分发挥其强度潜能，从而提高隧洞围岩稳定性，而且b越小，围岩稳定性状态对中间应力敏感度越高；

4)随着隧洞内压力Pi增大，围岩依次处于(2)中的3种状态，且当Pi≤σp2时，增大Pi有利于提高围岩稳定性，而当Pi>σp2时，围岩再次出现塑性破坏，且稳定性随Pi增大而降低。说明隧洞支护抗力(水工隧洞表现为隧洞内水压力)过小或过大都不利于隧洞围岩稳定性，上述结论为隧洞采取合理的支护强度提供科学依据。由于Mohr-Coulomb强度准则没有充分考虑中间主应力的影响，计算结果相对保守，且未能合理显示Pi过大时对围岩稳定性的不利作用。

References

[1] 王军祥，姜谙男.岩石弹塑性损伤本构模型建立及在隧洞工程中的应用[J].岩土力学，2015(4)：1 147-1 158.

WANGJun-xiang，JIANGAn-nan.Anelastoplasticdamageconstitutivemodelofrockanditsapplicationtotunnelengineering[J].RockandSoilMechanics，2015(4)：1 147-1 158.

[2]崔 岚，郑俊杰，章荣军，等.弹塑性软化模型下隧洞围岩变形与支护压力分析[J].岩土力学，2014(3)：717-722，728.

CUILan，ZHENGJun-jie，ZHANGRong-jun,etal.Studyofsupportpressureandsurroundingrockdeformationofacirculartunnelwithanelastoplasticsofteningmodel[J].RockandSoilMechanics，2014(3)：717-722，728.

[3]TalobreJA.Mecaniquedesroches[M].Paris：Dunod，1967.

[4]李咏偕，施泽华.塑性力学[M].北京：水利电力出版社，1987.

LIYong-xie,SHIZe-hua.Plasticmechanivs[M].Beijing:WaterResourcesandEleectricPowerPress,1987.

[5]HKastner.Statikdestunelundstollenbauess[M].Berlin：Springer-Verlag，1962.

[6]许东俊，耿乃光.岩石强度随中间主应力变化规律[J].固体力学学报，1985(1)：72-80.

XUDong-jun，GENGNai-guang.Thevariationlawofrockstrengthwithincreaseofintermediateprincipalstress[J].ActaMechanicaSolidaSinica，1985(1)：72-80.

[7]俞茂宏.工程强度理论[M].北京：高等教育出版社，1999.

YUMao-hong.Engineeringstrengththeory[M].Beijing:HigherEducationPress,1999.

[8]俞茂宏.岩土类材料的统一强度理论及其应用[J].岩土工程学报，1994，16(2)：1-10.

YUMao-hong.Unifiedstrengththeoryforgeoma-terialsanditsapplications[J].ChineseJournalofGeotechnicalEngineering，1994，16(2)：1-10.

[9]俞茂宏.双剪理论及其应用[M].北京：科学出版社，1998.

YUMao-hong.Theapplicationoftwinsheartheory[M].Beijing:SciencePress,1998.

[10]胡小荣，俞茂宏.统一强度理论及其在巷道围岩弹塑性分析中的应用[J].中国有色金属学报，2002(5)：1 021-1 026.

HUXiao-rong，YUMao-hong.Unifiedstrengththeoryanditsapplicationinelasto-plasticanalysistotunnel[J].TheChineseJournalofNonferrousMetals，2002(5)：1 021-1 026.

[11]王继秀，赵均海，王乐健，等.基于统一强度理论的井筒围岩应力分析[J].建筑科学与工程学报，2009(3)：105-109.

WANGJi-xiu，ZHAOJun-hai，WANGLe-jian，etal.Stressanalysisofwellborerockbasedonunifiedstrengththeory[J].JournalofArchitectureandCivilEngineering，2009(3)：105-109.

[12]张常光，张庆贺，赵均海.考虑应变软化、剪胀和渗流的水工隧洞解析解[J].岩土工程学报，2009，31(12)：1 941-1 946.

ZHANGChang-guang，ZHANGQing-he，ZHAOJun-hai.Analyticalsolutionsofhydraulictunnelsconsideringstrainsoftening，sheardilationandseepage[J].ChineseJournalofGeotechnicalEngineering，2009，31(12)：1 941-1 946.

[13]曾开华，鞠海燕，张常光.深埋圆形隧洞弹塑性位移统一解及其比较分析[J].岩土力学，2011(5)：1 315-1 319.

ZENGKai-hua，JUHai-yan，ZHANGChang-guang.Elastoplasticunifiedsolutionfordisplacementsaroundadeepcirculartunnelanditscomparativeanalysis[J].RockandSoilMechanics，2011(5)：1 315-1 319.

[14]郑颖人，沈珠江，龚晓南.岩土塑性力学原理[M].北京：中国建筑工业出版社，2002.

ZHENGYing-ren,SHENZhu-jiang,GONGXiao-nan.Theprinciplesofgeotechnicalplasticmechanics[M].Beijing:ChinaArchitectureandBuildingPress,2002.

[15]B.B.Соколовский.塑性力学[M].王振常,译.北京：建筑工程出版社，1957.

B.B.Соколовский.Plasticmechanics[M].WANGZhen-chang,translator.Beijing:ConstructionEngineer-ing,1957.

[16]徐芝纶.弹性力学[M].北京：人民教育出版社，1982.

XUZhi-guan.Elasticmechanics[M].Beijing:People’sEducationPress,1982.

[17]任青文，张宏朝.关于芬纳公式的修正[J].河海大学学报，2001，29(6)：109-111.

RENQing-wen，ZHANGHong-chao.Amodificationoffannerformula[J].JournalofHehaiUniversity，2001，29(6)：109-111.

Elastoplastic stress analysis of tunnel based on the unified strength criterion

GU Shuan-cheng1，HUANG Rong-bin1，SU Pei-li1，DING Xiao1，2，LI Ang1

(1.CollegeofCivilandArchitecturalEngineering,Xi’anUniversityofScienceandTechnology,Xi’an710054,China；2.SchoolofCivilandArchitectureEngineering，Xi’anTechnologicalUniversity，Xi’an710021，China)

Based on the unified strength theory，the elastic-plastic stress analysis is carried out under the premise that the first principal stress in two cases of radial stress and circumferential stress，and the formula of the radius of the surrounding rock and the plastic zone is derived.Tunnel surrounding rock has three states including the elastic state，the elastoplastic state that the maximum principal stress is the radial stress and the elastoplastic state that the maximum principal stress is the circumferential stress.When the elastic-plastic analysis was carried out on the tunnel，the state of the surrounding rock should be judged and the correct formula is chosen to calculate.Analysis results show that the intermediate principal stress is benefit to the rock to give full play to the strength of the potential，so as to improve the stability of surrounding rock of the tunnel and the smaller intermediate principal stress coefficient，the higher sensitivity of the surrounding rock stability to the intermediate stress.When the inside pressure is less than the second critical stress and increasing the hole pressure is beneficial to improving the stability of surrounding rock，while the hole pressure is greater than the second critical stress，the stability of surrounding rock will reduce with the increase of the hole pressure.

unified strength theory；tunnel surrounding rock；fenner formula；intermediate principal stress；elasto-plastic analysis

10.13800/j.cnki.xakjdxxb.2016.0608

1672-9315(2016)06-0806-07

2016-08-11 责任编辑：李克永

国家自然科学基金(51508462)；陕西省科学基础研究计划(2016JM4014)

谷拴成(1963-)，男，陕西省扶风人，博士生导师，E-mail：yikaiyizhi@qq.com

U 452

A