软岩巷道耦合支护最优化设计粘弹性分析
罗生虎,伍永平,张嘉凡
(1.西安科技大学 理学院,陕西 西安 710054;2.西安科技大学 西部矿井开采及灾害防治教育部重点实验室,陕西 西安 710054;3.西安科技大学 能源学院,陕西 西安 710054)
软岩巷道耦合支护最优化设计粘弹性分析
罗生虎1,2,伍永平2,3,张嘉凡1,2
(1.西安科技大学 理学院,陕西 西安 710054;2.西安科技大学 西部矿井开采及灾害防治教育部重点实验室,陕西 西安 710054;3.西安科技大学 能源学院,陕西 西安 710054)
在地下岩体工程中,无论是软岩还是硬岩,只要岩体受力后的应力水平达到或超过该岩体的流变下限,都将随着时间的增长而发生流变变形。针对深部矿井开采中的巷道支护问题,根据粘弹性理论,在考虑开挖面空间效应的基础上,建立巷道围岩与支护体的耦合作用模型;在此基础上,根据非线性最优化设计原理,建立巷道耦合支护的最优化设计模型。通过算例分析了支护时间、支护体厚度等因素对巷道围岩和支护体稳定性的影响以及对支护设计方案的影响。结果表明,巷道围岩的稳定性与支护时间、支护体厚度等因素密切相关。巷道位移随着支护时间的增大以及支护体厚度的减小而增大;支护体受力随着支护时间的增大以及支护体厚度的增大而减小。当支护体不发生破坏且巷道位移小于某一临界值时,支护体厚度随着支护时间的增大而先减小后增大。
围岩;粘弹性;耦合;最优化设计
0 引 言
巷道支护技术是矿井建设与地下开采中的一项关键技术,安全、合理、高效的巷道支护技术是保证矿井高产高效的必要条件[1-6]。随着采矿工程的发展,国内外学者通过理论和实验等手段对巷道支护问题进行了大量的研究,新奥地利隧道施工方法、轴变理论、联合支护技术等理论和技术被应用到巷道支护工程中,为解决某些具体的实际问题提供了强有力的理论和技术支撑[7-12]。
目前,在巷道耦合支护理论研究方面,较为成熟的理论仍是以弹塑性理论导出的围岩-支护结构作用理论。通过侯公羽[13]对卡斯特纳方程的分析研究可以看出,在卡斯特纳方程求解中,对支护反力的力学简化处理存在缺陷,不具有工程实际意义。在地下岩体工程中,无论是软岩还是硬岩,只要岩体受力后的应力水平达到或超过该岩体的流变下限,都将随着时间的增长而发生流变变形[14]。近年来,已有许多学者对巷道围岩的流变特性及其控制机理展开了研究,并取得了许多有价值的研究成果。王祥秋等[15]基于软弱围岩的蠕变损伤机理,在Burgers模型的基础上建立了围岩的流变损伤模型,采用位移反分析法研究了巷道合理的支护时间。刘保国等[16]在考虑巷道开挖面空间效应的基础上,推演了圆形隧洞围岩与支护结构之间相互作用的时效规律,对合理设计永久性支护结构具有指导意义。朱珍德等[17]对采用锚杆支护的巷道,根据Poynting-Thomson线性流变模型,分析了在两向等压条件下锚杆区围岩应力和位移随时间的变化规律,建立了与时间有关的锚杆支护破坏准则。一些学者通过分析支护体厚度、强度以及刚度等设计参数[17-19],并对设计参数进行优化,以期达到新奥地法所提出的既安全又经济的最佳支护状态[20-22]。但目前关于支护优化设计的研究较多是侧重于在原有支护基础上改进支护措施,或是通过多种设计方案对比分析,确定相对安全、经济、合理的设计方案,这些研究工作丰富了巷道支护优化设计的研究,但仍未给出最佳的巷道支护设计方案。上述研究工作为进一步的研究提供了有力的支撑,但所取得的这些成果,在日益复杂的工程实践中,还远未能达到有效解决和指导井巷工程施工的目的。
文中在前人研究的基础上,首先基于粘弹性理论,考虑巷道开挖面的空间效应,建立围岩与支护体耦合作用的流变模型,分析支护时间和支护体厚度等因素对巷道围岩以及支护体结构稳定性的影响;在此基础上,通过非线性最优化原理,建立巷道支护的最优化设计模型,分析巷道支护的最优化设计方案,以期为巷道支护设计提供科学的理论依据和指导。
1 基本模型
巷道力学模型如图1所示,为了理论求解方便,做如下假设。

图1 巷道力学模型Fig.1 Mechanical model of the rock tune
1)巷道围岩和支护体可视为是连续、均匀以及各向同性的材料,可用线性粘弹性模型模拟巷道围岩的实效特征;
2)巷道深埋,处于静水应力场中,初始地应力为p0;
3)巷道围岩与支护体在交界面上满足应力和位移的连续性条件;
4)巷道断面一次开挖成型,巷道半径为R0;
5)巷道开挖(掌子面推进)是一个三维的过程,为了避免三维问题在计算中带来的困难,用作用在巷道内虚拟的支护力f(t)等效纵向开挖所造成的三维效应。根据已有的研究结果,其可表示为[16,19]
f(t)=p0(1-0.7exp(-mt)).
(1)
式中m=3.15v/2R0;v为巷道开挖面推进速度;
6)支护体在t1时刻瞬间施工完成,并产生支护效应。
根据以上基本假设,原有的三维问题可简化为平面应变问题。整个过程可分为2个阶段,当0≤t 假设巷道围岩为粘弹性体,简化期间,设其流变模型可表示为广义开尔文(General Kelvin)体,如图2所示,当巷道围岩满足其它类型的线性流变模型时,可采用相同的处理方式。其本构方程可表示为[23] (2) 则其蠕变柔量可表示为 3.1 巷道围岩的应力和位移 由弹性力学知识可知巷道围岩在载荷f( t) 作用下产生的应力和位移可描述为[24] 式中 μ0和Er0为巷道围岩的泊松比和弹性模量。 (7) 式中,上标~表示对该量进行Laplace变换,下同。 (8) Δu0r′(R0,t)=u0r′(R0,t)-u0r′(R0,t1)=A1{1-exp[-k1(t-t1)]}+A2{1-exp[-m(t-t1)]}. (9) 式中 A1和A2为常量, 当支护体架设之后,在巷道围岩流变以及开挖面空间效应的影响下,巷道围岩和支护体在交界面上会产生相互作用力p(t)。则巷道围岩在支护力p(t)作用下产生的应力和位移为[24] (10) (11) (12) 根据弹性-粘弹性对应原理,则巷道围岩的径向位移u0r″(R0,t)的粘弹性解在象空间的表达式为[16,23] (13) 式中 p(t)为时间t的未知函数,根据卷积定理可将其表示成积分形式。则式(13)的Laplace逆变换可表示为 ur″(R0,t)= (14) 则从t1到t时刻,巷道围岩在载荷p(t)作用下,在其与支护体交界面R0处产生的位移增量Δu0r″(R0,t)可表示为 (15) 式中 A3为常数,A3=(1+μ0)R0. (16) 3.2 支护体的应力和位移 这里假设支护体为弹性体,不考虑支护体的流变变形。则由弹性理论知识可知,支护体的应力和位移可表示为[24] (17) (18) (19) 式中 μ1和El1为支护体的泊松比和弹性模量。 (20) 式中 A4为常数, 3.3 变形协调条件 根据位移连续性假定,巷道围岩与支护体在接触面上从t1到任意t时刻,二者的径向位移增量相等,即[16,19,24] (21) 将式(16)和(20)带入式(21),得 (22) 整理上式得 (23) 式中 A5为常数,A5=A4-A3/E0. 令ζ=τ+t1,则dζ=dτ.并令T=t-t1,则式(23)变为 (24) 对式(24)进行Laplace变换,得 (25) 整理上式得 (26) 式中 B1,B2,B3为常量, 对式(26)做恒等变换得 (27) 式中 C1,C2,C3为常量, 对式(27)进行Laplace逆变换,得 p(t)=C1+C2exp[-m(t-t1)]+C3exp[-B3(t-t1)]. (28) 由式(28)可以看出,当时间t趋向于无穷大时,新增应力p(t)趋向于C1. 则对应的巷道围岩应力和巷道位移可表示为 (30) (31) (32) 下面将分析支护时间、护体厚度、巷道断面以及原岩应力对巷道围岩流变稳定性的影响。表1为计算中所需的相关物理参量,参量的值是根据已有的文献中选取的标准值[16]。 表1 模型中相关物理参量 4.1 支护时间对巷道稳定性的影响 这里取原岩应力为10 MPa,巷道半径为3 m,支护体厚度为0.2 m,支护时间依次取为2,5,10和15 d,分析支护时间对巷道围岩稳定性的影响。 图3 支护时间对巷道位移的影响Fig.3 Effect of support time on the displacement 图3和图4所示为在不同支护时间条件下,巷道位移和支护体内径处环向应力随时间的变换规律。由图中可以看出,随着支护时间的后移,巷道位移逐渐增大,而环向应力逐渐减小。巷道位移和环向应力随时间的变化规律基本一致,均呈现出在巷道开挖初期变形剧烈,都随时间的增长而迅速增大;经过初期的剧烈变化后,逐渐趋于平缓,并最终趋于某一稳定值。当支护时间从巷道开挖后2 d后移到5,10以及15 d时,巷道位移分别增大了32%,67%和97%;支护体内径处环向应力分别减小了13%,19%和27%.可以看出支护时间对巷道围岩的稳定性有重要的影响。 图4 支护时间对支护体环向应力的影响Fig.4 Effect of support time on the hoop stress 4.2 支护体厚度对巷道稳定性的影响 这里取原岩应力为10 MPa,巷道半径为3 m,支护时间为2 d,支护体厚度依次取为0.1,0.2,0.3和0.4 m,分析支护体厚度巷道围岩稳定性的影响。 图5 支护体厚度对巷道位移的影响Fig.5 Effect of thickness of liner on the displacement 图6 支护体厚度对支护体环向应力的影响Fig.6 Effect of thickness of liner on the hoop stress 图5和图6所示为在不同支护体厚度条件下,巷道位移和支护体内径处环向应力随时间的变换规律。由图中可以看出,随着支护体厚度的增大,巷道位移和环向应力都逐渐减小。当支护体厚度从0.1 m增大到0.2,0.3及0.4 m时,巷道位移分别减小了23%,31%和36%;支护体内径处环向应力分别减小了45%,62%和71%.可以看出支护厚度对阻止巷道收敛有重要的影响。 4.3 原岩应力对巷道稳定性的影响 这里取巷道半径为3 m,支护体厚度为0.2 m,支护时间为2 d,原岩应力依次取为5,10,15和20 MPa,分析原岩应力对巷道围岩稳定性的影响。 图7 原岩应力对巷道位移的影响Fig.7 Effect of rock stress on the displacement 图8 原岩应力对支护体环向应力的影响Fig.8 Effect of rock stress on the hoop stress 图6和图7所示为在不同原岩应力条件下,巷道位移和支护体内径处环向应力随时间的变换规律。由图中可以看出,随着原岩应力的增大,巷道位移和环向应力也逐渐增大。当原岩应力从5 MPa增大到10,15和20 MPa时,巷道位移和支护体内径处的环向应力都分别增大了100%,200%和300%. 4.4 巷道断面对巷道稳定性的影响 这里取原岩应力为10 MPa,支护时间为2 d,支护体厚度为0.2 m,巷道半径依次取为2,2.5,3和3.5 m,分析巷道半径对巷道围岩稳定性的影响。 图9 巷道断面对巷道位移的影响Fig.9 Effect of road section on the displacement 图10 巷道断面对支护体环向应力的影响Fig.10 Effect of road section on the hoop stress 图9和图10所示为在不同巷道断面条件下,巷道位移和支护体内径处环向应力随时间的变换规律。由图中可以看出,随着巷道断面的增大,巷道位移和支护体内径处的环向应力也逐渐增大。当巷道半径从2 m增大到2.5,3以及3.5 m时,巷道位移分别增大了26%,53%和82%;支护体内径处环向应力分别增大了22%,45%和68%. 由以上分析可以看出,在地下井巷工程中,巷道围岩的稳定性与支护时间、支护体厚度等因素密切相关,支护时间越早、支护体厚度越大,巷道位移就越小,巷道围岩也就越稳定。在实际支护工程中,在巷道断面和围岩应力等客观因素给定的情况下,施工人员所面临的关键问题就是何时支护以及以何种方式支护,这也是巷道支护研究的焦点问题。新奥地利隧道施工方法是目前地下工程设计的主要方法之一,采用初期支护和二次支护的复合式支护。其中,对于二次支护时机的确定,王祥秋等[15]从围岩流变的角度出发,建立巷道围岩的流变力学模型,通过位移反分析法对二次支护时间进行了研究,让围岩的弹塑性变形得到有效释放(即,巷道位移趋于稳定)后再进行支护;但对于初次支护方案的设计,目前仍处于探索阶段,支护设计仍基本以经验为主,使得在实际工程中经常发生还未来得及进行二次支护巷道已经破坏。从图4和图6中可以看出,在巷道开挖面空间效应以及围岩流变等因素的影响下,支护体的内径处的环向应力在不断增大,如果支护时间过早或是支护体厚度过小,在还未进行二次支护时,支护体就有可能已经发生破坏,但是如果单方面的从增加支护厚度去保证巷道安全,又势必会造成不必要的浪费。可以看出,如何达到新奥法提出的既安全又经济的最佳支护状态,是巷道支护工程势必要解决的问题。 基于以上分析,文中根据非线性最优化设计原理,从保证巷道安全和降低工程造价2方面考虑,建立巷道支护的最优化设计模型,以期达到新奥法提出的既安全又经济的最佳支护状态。 首先,从保证巷道安全的角度出发,巷道围岩越稳定越好,这里用巷道位移来表征巷道围岩的稳定性,要求巷道位移越小越好,且要求巷道位移必须小于等于实际工程所容许的临界值ucr,即 minu0r(R0,h,t1), (33) u0r(R0,h,t1)≤ucr, (34) 其次,从经济的角度出发,巷道支护耗材越少越好,这里用单位厚度支护体的体积来表征,即 (35) 最后,为保证巷道安全,要求支护体不发生破坏。这里用支护体是否发生塑性变形作为判定巷道安全与否的条件,则由Mohr-Coulomb准则可得 (36) 式中σ0为混凝土的许用应力。 基于以上分析可以看出,巷道支护优化模型中的决策变量取为支护时间t1和支护体厚度h;目标函数取为巷道位移和单位厚度的支护体体积;约束条件取为支护体不发生塑性变形和巷道位移小于等于某一临界值。则其对应的巷道支护最优化设计模型可表示为[25] minV(h) minu0r(R0,h,t) (37) s.t.u0r(R0,h,t)≤ucr h,t1>0 式(37)中位移和应力的具体表述形式可根据耦合模型中的计算结果得出。 可以看出,这是一个多目标非线性的最优化问题,文中采用共轭梯度法求解。对于具体工程问题,可根据实际要求设定决策变量、目标函数以及约束条件等。 表2 巷道支护优化设计参数 上述模型是一个两自由度的最优化模型,在满足实际要求的情况下,有2个参量可进行自由匹配,并最终获取最优的设计参数。但在实际工程中,支护时间或支护体厚度可能是预先设计的。例如,在上述约束条件不变的情况下,当支护时间确定时,与之匹配的支护体厚度应该为多少;或者当支护体厚度确定时,与之匹配的支护时间应该为多少。这实际上是将上述模型简化为单自由度的优化模型,为此只需在上述模型中对某一参量按照实际要求取为常量,即可求出与之匹配的另一个参量值。 表3 支护体厚度优化设计 表3给出了在支护时间确定的情况下与之匹配的支护体厚度。由表中可以看出,在约束条件不变的情况下,随着支护时间的增大,支护体厚度先减小后增大。这反映出,当支护时间较早时,原岩应力没有得到有效释放,因此在这种情况下,当围岩变形处于稳定状态时,支护体所承受的载荷较大,当支护体受力处于临界状态时,巷道位移并没有达到事先设定的临界值。随着支护时间的增大,巷道原岩应力逐步得以有效释放,当围岩变形处于稳定状态时,且支护体受力处于临界状态时对应的支护体厚度也在逐渐减小,巷道位移逐渐趋向于事先设定的临界值。当支护时间大于某一临界值时,要保证巷道位移小于等于事先设定的临界值,只能通过增加支护体厚度来实现,即支护体厚度随着支护时间的增大而增大,但此时支护体的受力明显没有达到临界状态。 表4 支护时间优化设计 注:***表示模型求解失败,无法获取支护时间。 表4给出了在支护体厚度确定的情况下与之匹配的支护时间。由表中可以看出,当支护体厚度较小时,优化模型无法求出与之匹配的支护时间,即支护设计失效;当支护体厚度大于某一临界值后,支护时间随着支护体厚度的增大而减小。表中给出了支护失效情况下,当支护体受力处于临界状态时对应的ucr-u0,可以看出,此时的巷道位移已大于模型中事先设定的临界值ucr,已不满足模型中的约束条件,因此无法获取与之匹配的支护时间。这实际上反映出,当支护体厚度较小时,如果支护时间较早,就无法保证支护体的稳定性,如果支护时间较晚又无法保证巷道围岩的稳定性(即,巷道位移大于了事先设定的临界值)。因此在实际工程中因综合考虑各因素的影响,合理的架设支护体。 在考虑了巷道开挖面空间效应的基础上,根据粘弹性理论建立了巷道围岩与支护体的耦合作用模型,并在此基础上,通过非线性最优化设计原理,建立了巷道支护的最优化设计模型。研究结果显示 1)通过围岩与支护体耦合作用的粘弹性模型,分析了各因素对围岩-支护体流变稳定性的影响。结果显示,支护时间、支护体厚度等因素都与与巷道围岩和支护体的稳定性密切相关。巷道位移随着支护时间的增大以及支护体厚度的减小而增大,支护体内径处的环向应力随着支护时间的增大以及支护体的增大而减小; 2)通过建立巷道支护的优化设计模型,分析了支护时间和支护体厚度对巷道支护设计方案的影响,给出了在满足实际约束条件下的最优化设计参数,达到了优化设计的目的。在支护时间确定的情况下,支护体厚度随着支护时间的增大而先减小后增大;而当支护体厚度确定的情况下,当支护体厚度较小时会发生支护失效的可能,并且随着支护体厚度增大,支护时间在逐渐减小; 3)文中只是针对圆形断面巷道探讨了围岩与支护体的耦合作用关系,并在此基础上给出了巷道支护的优化设计模型,与实际的支护情况仍有一定的差距。但从文中的模型中可以看出,巷道支护与开挖面空间效应、支护时间以及支护体的力学特性等因素密切相关,是一个复杂的耦合过程。在实际工程中,应根据工程实际要求,结合工作面的空间效应、围岩和支护体的力学特性等因素,合理架设支护体。 References [1] 于学馥,郑颖人,刘怀恒,等.地下工程围岩稳定分析[M].北京:煤炭工业出版社,1983. YU Xue-fu,ZHENG Ying-ren,LIU Huai-heng,et al.Surrounding rock stability analysis in underground engineering[M].Beijing: China Coal Industry Press,1983. [2]何满潮.深部软岩工程的研究进展与挑战[J].煤炭学报,2014,39(8): 1 409-1 417. HE Man-chao.Progress and challenges of soft rock engineering in depth[J].Journal of China Coal Society,2014,39(8):1 409-1 417. [3]伍永平,刘孔智,贠东风,等.大倾角煤层安全高效开采技术研究进展[J].煤炭学报,2014,39(8): 1 611-1 618. WU Yong-ping,LIU Kong-zhi,YUN Dong-feng,et al.Research progress on the safe and efficient mining technology of steeply dipping seam[J].Journal of China Coal Society,2014,39(8): 1 611-1 618. [4]康红普,王金华,李玉梅,等.掘进工作面围岩应力分布特征及其与支护的关系[J].煤炭学报,2009,23(7): 145-150. KANG Hong-pu,WANG Jin-hua,LI Yu-mei,et al.Stress distribution characteristics in rock surrounding heading face and its relationship with supporting[J].Journal of China Coal Society,2009,23(7): 145-150. [5]谢和平,周宏伟,薛东杰,等.煤炭深部开采与极限开采深度的研究与思考[J].煤炭学报,2012,37(4): 535-542. XIE He-ping,ZHOU Hong-wei,XUE Dong-jie,et al.Research and consideration on deep coal mining and critical mining depth[J].Journal of China Coal Society,2012,37(4): 535-542. [6]何满潮,谢和平,彭苏萍,等.深部开采岩体力学研究[J].岩石力学与工程学报,2005,24(16):2 803-2 813. HE Man-chao,XIE He-ping,PENG Su-ping,et al.Study on rock mechanics in deep mining engineering[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(16): 2 803-2 813. [7]柳选军,刘庆利,朱世阳,等.深井长距离大断面回采巷道支护方案优化[J].西安科技大学学报,2015,35(1): 28-31. LIU Xuan-jun,LIU Qing-li,ZHU Shi-yang,et al.Supporting scheme optimization for long distance and large dimension entry of deep mine[J].Journal of Xi’an University of Science and Technology,2015,35(1): 28-31. [8]吕兆海,来兴平,来红祥,等.大采高工作面穿越断层破碎区预注浆耦合加固实践[J].西安科技大学学报,2014,34(6): 670-675. LV Zhao-hai,LAI Xing-ping,LAI Hong-xiang,et al.Coupled strengthening by pre-grouting practice on large mining height working face through the fault fracture zone[J].Journal of Xi’an University of Science and Technology,2014,34(6): 670-675. [9]丁国峰,王苏健,谢文兵,等.加固顶板和两帮控制回采巷道底臌研究[J].西安科技大学学报,2014,34(4): 384-389. DING Guo-feng,WANG Su-jian,XIE Wen-bing,et al.Mechanism of reinforcing roof and sides for floor heave control of roadway[J].Journal of Xi’an University of Science and Technology,2014,34(4): 384-389. [10]张雪媛.深井岩巷破坏机理与支护优化研究[J].西安科技大学学报,2014,34(4): 390-395. ZHANG Xue-yuan.Failure mechanism and support optimization of deep rock roadway[J].Journal of Xi’an University of Science and Technology,2014,34(4): 390-395. [11]刘巨海.水对灰质泥岩隧道围岩稳定性影响研究[J].西安科技大学学报,2014,34(3): 302-308. LIU Ju-hai.Influence of water on the stability of surrounding rock in lime mudstone tunnel[J].Journal of Xi’an University of Science and Technology,2014,34(3): 302-308. [12]冯晓光,任建喜,谷拴成,等.公路隧道围岩现场快速分级方法研究[J].西安科技大学学报,2013,33(3): 277-282. FENG Xiao-guang,REN Jian-xi,GU Shuan-cheng,et al.On-site rapid classification method of surrounding rock in highway tunnel[J].Journal of Xi’an University of Science and Technology,2013,33(3): 277-282. [13]侯公羽.围岩-支护作用机制评述及其流变变形机制概念模型的建立与分析[J].岩石力学与工程学报,2008,27(增刊2): 3 618-3 629. HOU Gong-yu.Review of interaction mechanism between surrounding rock and analysis of conceptual model of theological deformationmechanism[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(Supp.2): 3 618-3 629. [14]孙 钧.岩石流变力学及其工程应用研究的若干进展[J].岩石力学与工程学报,2007,26(6): 1 081-1 106. SUN Jun.Rock rheological mechanics and its advance in engineering applications[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(6): 1 081-1 106. [15]王祥秋,杨林德,高文化.软弱围岩蠕变损伤机理及合理支护时间的反演分析[J].岩石力学与工程学报,2004,23(5): 793-796. WANG Xiang-qiu,YANG Lin-de,GAO Wen-hua.Creep damage mechanism and back analysis of optimum support time for soften rock mass[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(5): 793-796. [16]刘保国,杜学东.圆形洞室围岩与结构相互作用的黏弹性解析[J].岩石力学与工程学报,2004,23(4): 561-564. LIU Bao-guo,DU Xue-dong.Viscoelastical analysis on interpaly berween supporting structure and surrounding rocks of circle tunnel[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(4): 561-564. [17]朱珍德,王玉树.巷道围岩流变对巷道稳定性的影响[J].力学与实践,1998,20(1): 26-29. ZHU Zhen-de,WANG Yu-shu.Influence of roadways surrounding rock’srehology on stability of roadways[J].Mechanics and Practice,1998,20(1): 26-29. [18]Wang H N,Utili S,Jiang M J.An approach for the sequential excavation of axisymmetric lined tunnels in viscoelastic rock[J].International Journal of Rock Mechanics and Mining Sciences,2014,68(6): 85-106. [19]勾攀峰,辛亚军.深井巷道围岩锚固体流变控制力学解析[J].煤炭学报,2013,38(12): 2 019-2 025. GOU Pan-feng,XIN Ya-jun.Rheological control mechanical analyticity of surrounding rock anchorage body in deep roadway[J].Journal of China Coal Society,2013,38(12): 2 019-2 025. [20]张向东,李永靖,张树光,等.软岩蠕变理论及其工程应用[J].岩石力学与工程学报,2004,23(10):1 635-1 639. ZHANG Xiang-dong,LI Yong-jing,ZHANG Shu-guang,et al.Creep theory of soft rock and its engineering application[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(10):1 635-1 639. [21]华心祝,吕凡任,谢广祥.锚注软岩巷道流变研究[J].岩石力学与工程学报,2003,22(2): 297-303. HUA Xin-zhu,LV Fan-ren,XIE Guang-xiang.Rheological study on bolt-grouting supported roadways in soft rock[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(2): 297-303. [22]韦四江,勾攀峰.锚杆预紧力对锚固体强度强化的模拟实验研究[J].煤炭学报,2012,37(12): 1 987-1 993. WEI Si-jiang,GOU Pan-feng.Analogy simulation test on strengtheningeffect for pretention of bolts on anchorage body[J].Journal of China Coal Society,2012,37(12):1 987-1 993. [23]杨挺青.粘弹性力学[M].武汉:华中理工大学出版社,1990. YANG Ting-qing.Viscoelastic mechanics[M].Wuhan: Huazhong University of Science and Technology Press,1990. [24]王龙甫.弹性理论[M].北京:科学出版社,1984. WANG Long-pu.Elastic theory[M].Beijing: Science Press,1984. [25]解可新,韩立兴,林友联.最优化方法[M].天津:天津大学出版社,1997. XIE Ke-xin,HAN Li-xing,LIN You-lian.Optimization method[M].Tianjin:Tianjin University Press,1997. Visco-elastical analysis on optimized design of coupling support for soft rock roadway LUO Sheng-hu1,2,WU Yong-ping2,3,ZHANG Jia-fan1,2 (1.CollegeofSciences,Xi’anUniversityofScienceandTechnology,Xi’an710054,China; 2.KeyLaboratoryofWesternMineExplorationandHazardPreventionMinistryofEducation,Xi’anUniversityofScienceandTechnology,Xi’an710054,China;3.CollegeofEnergyScienceandEngineering,Xi’anUniversityofScienceandTechnology,Xi’an710054,China) In the underground rock engineering,the mechanical properties of surrounding rock mass exhibits time-dependent,as long as the rock mass stress level reaches or exceeds the rock rheological limit.In view of the roadway problems of underground mining on the soft rock roadway,based on the theory of viscoelasticity,a model of coupling action between rock and supporting body is built with considering the spatial effect of excavation face.On this basis,based on the theory of nonlinear optimization principle,an optimization model of roadway support is established.The influences of the support time and the thickness of the supporting body on the deformation are analyzed,and the optimal design parameter of the roadway support is discussed in detail by a case study.The results show that support time and the thickness of the supporting body have a certain impact on the deformation.With increases roadway support time and increases supporting body thickness,the displacement increases.When the supporting body is safe and the roadway displacement is less than a critical value,the thickness of the supporting body decrease firstly with the increasing of the support time,and increase later. surrounding rock;viscoelasticity;coupling;optimized design 2016-03-15 责任编辑:李克永 伍永平(1962-),男,陕西汉中人,博士,教授,E-mail:wuyp@xust.edu.cn 10.13800/j.cnki.xakjdxxb.2016.0601 1672-9315(2016)06-0759-10 TD 823 A2 围岩流变力学特性

3 巷道围岩-支护体流变力学解析






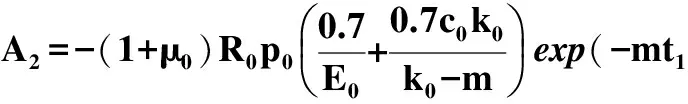















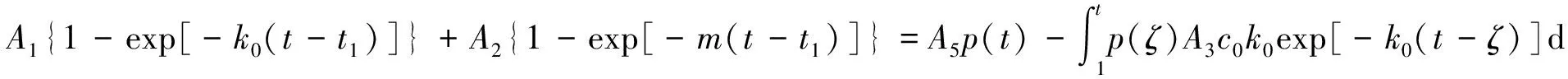











4 围岩流变影响参数分析









5 巷道耦合支护最优化设计






6 结 论

