内容分块算法中预期分块长度对重复数据删除率的影响

王龙翔,董小社,张兴军,王寅峰,公维峰,魏晓林

(1.西安交通大学电子与信息工程学院,710049,西安;2.深圳信息职业技术学院软件学院,518172,广东深圳;3.浪潮集团高效能服务器和存储技术国家重点实验室,250101,济南)



内容分块算法中预期分块长度对重复数据删除率的影响

王龙翔1,董小社1,张兴军1,王寅峰2,公维峰3,魏晓林1

(1.西安交通大学电子与信息工程学院,710049,西安;2.深圳信息职业技术学院软件学院,518172,广东深圳;3.浪潮集团高效能服务器和存储技术国家重点实验室,250101,济南)

针对基于内容分块重复数据删除方法缺少能够定量分析预期分块长度与重复数据删除率之间关系的数学模型,导致难以通过调整预期分块长度优化重复数据删除率的问题,提出了一种基于Logistic函数的数学模型。在大量真实数据测观察基础上,提出了通过Logistic函数描述非重复数据的“S”形变化趋势,解决了该数据难以从理论上推导、建模的问题,证明了基于内容分块过程服从二项分布,并从理论上推导出了元数据大小模型。基于上述两种数据模型,通过数学运算最终推导得到重复数据删除率模型,并利用收集到的3组真实数据集对模型进行了实验验证。实验结果表明:反映数学模型拟合优度的R2值在0.9以上,说明该模型能够准确地反映出预期分块长度与重复数据删除率之间的数学关系。该模型为进一步研究如何通过调整预期分块长度使重复数据删除率最优化提供了理论基础。

基于内容分块;重复数据删除率;Logistic函数

重复数据删除是一种数据精简技术,是应对大数据时代下数据存储规模越来越庞大这一问题的重要解决方案,目前在备份、归档等二级存储系统中得到了广泛应用[1-5],并有逐渐在文件系统等主存储系统中大量应用的趋势[6-7]。基于内容的分块算法[8]能够避免数据更新敏感问题,显著提高重复数据识别效率,是目前基于重复数据删除存储系统应用最广泛的分块算法。重复数据删除率反映了重复数据删除能够消除的重复数据比例,是衡量重复数据删除去重效果的基本指标,因此,提高重复数据删除率成为了一项重要研究。在进行重复数据删除后主要需要存储两类数据:非重复数据与元数据。非重复数据是指经过重复数据检测被判定为存储系统尚未存储过的数据;元数据是为了重构数据流需要保存的数据块在存储系统中的地址信息。预期分块长度是基于内容分块算法中需要预先设置的参数值,该值设置越小,所形成的数据块粒度越小,重复数据检测效率越高,但是也会产生更多的分块,使得元数据存储大小增加。因此,预期分块长度会显著影响重复数据删除率,该参数是基于内容分块算法中需要预先设置的一个重要参数[9],研究者指出通过合理设置预期分块长度能够显著提高重复数据删除率[10]。然而,已有研究主要通过改进基于内容分块算法来提高重复数据删除率,如何合理设置预期分块长度以提高重复数据删除率,却未引起研究者的重视。目前,研究者普遍根据经验认为4 kB[11]或者8 kB[5,8,12-13]是预期分块长度的合理值,但是这种设置方法既缺少理论上的证明也没有通过真实数据集进行验证。为了验证预期分块长度设置为4 kB或者8 kB在实际中能否使重复数据删除率最优,本文收集了3组真实数据集用于实验验证,分别为:①Linux内核源代码;②维基百科网页转储数据;③SQLite备份数据集。实验结果表明,预期分块长度设置为4 kB或者8 kB并不能使重复数据删除率最优。为了揭示预期分块长度与重复数据删除率之间隐含的数学关系从而更加合理地设置预期分块长度,本文提出了一种基于Logistic函数的数学模型描述预期分块长度与重复数据删除率之间的数学关系。基于3组真实数据集对数学模型进行了验证,结果表明,反映数学模型拟合优度的R2值基本在0.9以上,说明本文数学模型能够准确地描述预期分块长度与重复数据删除率之间的关系。

1 基于内容分块算法的原理

基于内容分块算法的主要原理如图1所示。通过设置大小为48 B的滑动窗口,从数据流的起始处开始滑动,并计算窗口内数据的Rabin指纹值[14];通过将Rabin指纹值和掩码值进行“与”操作,判断所得结果是否等于一个预先设定的魔数。如果以上条件成立,则将当前窗口的最后一个字节作为分块的边界点,当窗口在数据流中滑动结束后,所形成的边界点将数据流划分为长度不同的一系列数据块集合。为了避免出现分块过大或过小的情况,可设置分块大小的最小值与最大值,当分块大小小于最小值时,舍弃当前边界点;当分块大小大于最大值时,强制设置当前窗口最后一个字节为边界点。

在基于内容分块算法中,预期分块长度μ由掩码长度x决定,两者存在指数关系。

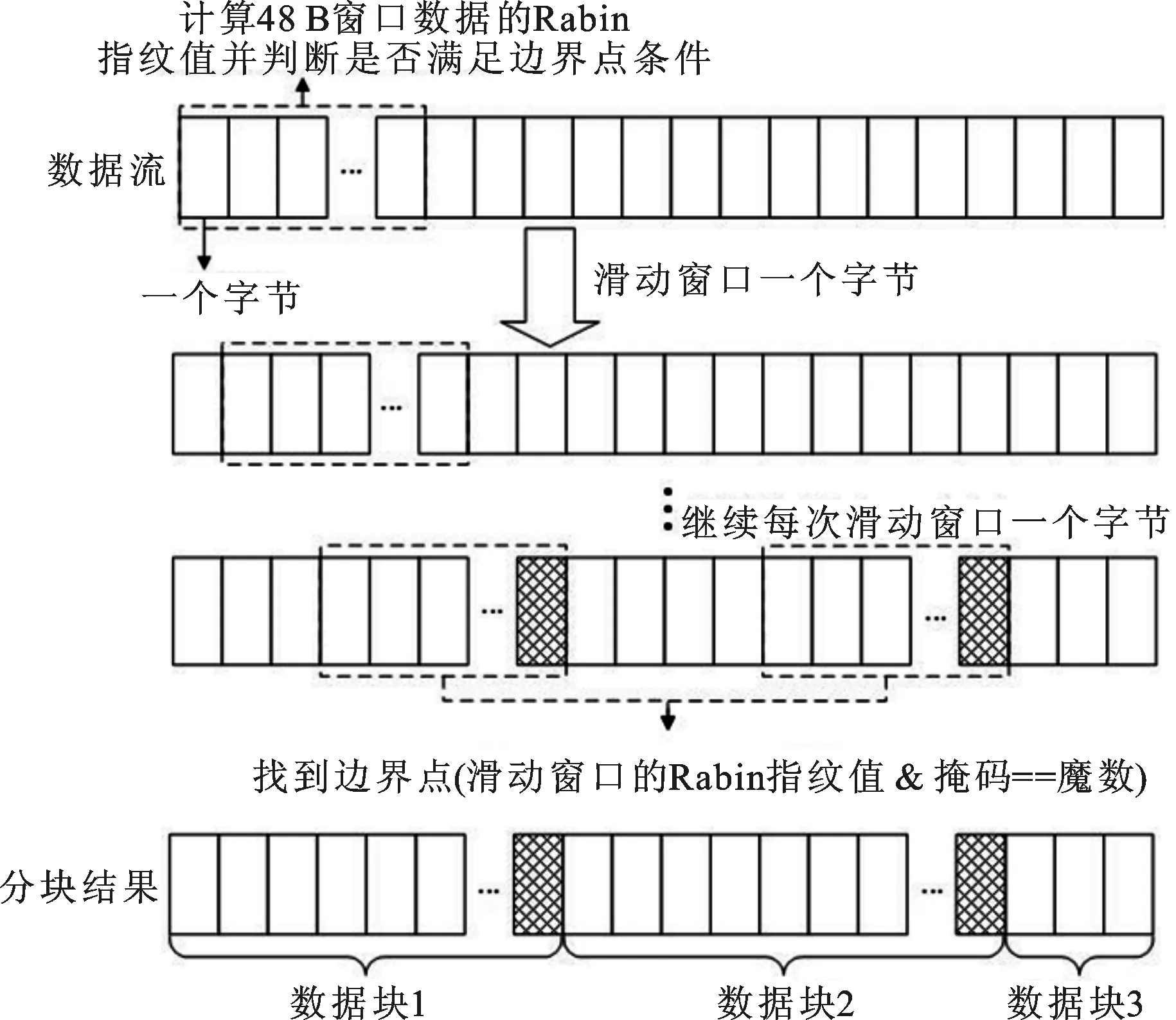
图1 基于内容分块算法的原理

2 重复数据删除率与预期分块长度的建模

在进行重复数据删除后需要存储的数据为:①非重复数据块,即经过基于内容分块算法分块后判定为尚未存储过的数据块;②元数据,为了重构数据流需要保存的数据块实际存储地址信息。③指纹值,所有非重复数据块对应的MD5/SHA-1指纹值信息。与前两种数据相比,由于指纹值存储空间很小,对重复数据删除率的影响可忽略不计,因此本文的建模中忽略指纹值。

2.1 元数据大小建模

经过分块算法对数据流进行切分后所形成的每一个数据块,无论其是否重复都需要保存对应的元数据信息。元数据主要是当前数据块在重复数据删除系统中的实际存储地址信息,用于在系统进行恢复时取回对应的数据块。数据流对应的元数据数量Nm等于总分块数量

(1)

式中:So代表原始数据大小;μ代表预期分块长度;x代表基于内容分块算法中设置的掩码长度。

假设每条元数据大小为m,则元数据大小为

(2)

2.2 非重复数据大小建模

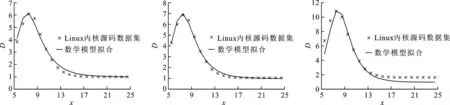
非重复数据大小与预期分块长度之间的关系无法从理论上直接进行推导。本文通过对大量真实数据集进行实验观察后发现:非重复数据与预期分块长度之间的关系曲线呈现S型,增长率表现出先急后缓的趋势,并且曲线有上界,该曲线符合Logistic函数曲线的特征。图2是本文所观察的真实数据集中非重复数据大小与预期分块长度(该长度是掩码长度的指数函数)之间关系曲线的典型代表,3组数据分别是Linux内核310个版本数据、维基百科网站12次转储数据、SQLite 90次备份数据。

Logistic函数的定义为

Logistic(x)=L/(1+exp(-k(x-x0)))

(3)

式中:L是Logistic函数的上界;k为函数陡峭程度;x0是函数增长率发生变化的横坐标值。

在基于内容分块算法中,非重复数据大小的上界为去重前的数据大小So,因此,非重复数据大小Su的数学模型为

(4)

2.3 重复数据删除率建模

进行重复数据删除处理后需要存储的数据总大小Sd等于元数据大小Sm与非重复数据大小Su之和,其数学关系为

Sd=Su+Sm=

(5)

根据重复数据删除率的定义,可推导重复数据删除率D与预期分块长度μ关系的数学模型为

(6)

(a)Linux内核数据集3.0～3.5.2

(b)维基百科数据集

(c)SQLite数据集图2 真实数据集中非重复数据大小与基于内容分块算法中设置的掩码长度之间的关系

式中:m为单个元数据大小,其数值取决于具体的系统实现,为常量。k与x0在式(6)中属于需要确定的参数。式(6)分母中1/(1+exp(-k(x-x0)))随着x的增大而增大,m/2x随着x的增大而减小,并且减小速率会逐渐变小。因此,式(6)分母的变化趋势在x值较小时由m/2x决定,随着x的增大而减小;之后由1/(1+exp(-k(x-x0)))决定,随着x的增大而增大。D则先随着x的增大而增大,后随着x的增大而减小。这种变化趋势符合实际中重复数据删除率的变化规律,因此,从理论上分析,式(6)可作为重复数据删除的数学模型。

3 实 验

3.1 实验环境

本文采用开源重复数据删除软件deduputil[15]作为测试程序,deduputil软件支持多种分块方式,包括基于内容分块。

测试所使用服务器配置为:2个IntelE5-2650v2(2.6GHz/8c)/8GT/20M处理器;128GBDDR3内存;1.2TMLCSSDPCIe接口磁盘;CentOSrelease6.5(Final)操作系统。

3.2 数据集

本文收集了3组真实数据集用于实验测试,分别为:①Linux内核源码数据集[16],总大小为233.95GB,包括版本3.0～3.4.63,共260个版本;②维基百科转储数据集[17],来自于Wikipedia网站部分页面定期的转储数据,总大小为11GB,共12次转储;③SQLite备份数据集[18],即SQLite数据库在运行TPC-C[19]测试程序后自动备份得到的数据集,总大小为148GB,共90次备份。

由于真实存储系统中数据规模会不断增大,为了更全面地观察实验结果,本文模拟了真实存储系统中数据的特点,将3组数据集的数据规模由小到大分别进行了测试。在Linux内核测试中,将前60个版本作为第一次测试,之后每间隔100个版本进行一次测试,即分别测试前60个版本,前160个版本,最后的260个版本;Wikipedia数据集前4个转储数据作为第一次测试,之后每间隔4个转储数据进行一次测试;SQLite数据集前10个备份数据作为第一次测试,之后每间隔40个备份数据进行一次测试。在基于内容的分块算法中需要设置分块最小值与最大值参数,本文设置最小值为64B,最大值为32MB。因此,实验中设置需要观察的预期分块长度范围为64B～32MB,对应x范围为5～25。

3.3 实验结果

实验结果如图3～5所示,结果表明:在所有测试中,将预期分块长度设置为4kB或者8kB都不能使重复数据删除率最优。此外,实验结果还表明,不同类型数据集,重复数据删除率最优的预期分块长度不同,即使同一类型数据集,随着数据规模的增大,最优重复数据删除率对应的预期分块长度也会发生变化,因此,按照经验将预期分块长度设置为某个固定值无法使重复数据删除率最优。

本文通过R2值反映所提出重复数据删除率数学模型与实际曲线的拟合程度,其取值范围为0～1,越接近于1说明数学模型拟合效果越好。图3～5表明,测试结果的R2值均在0.9以上,并且数据规模越大,拟合程度越高,说明本文所提出的重复数据删除率的数学模型能够准确反映出真实数据集中重复数据删除率与预期分块长度之间的数学关系。

(a)Linux内核源码3.0～3.0.60 (b)Linux内核源码3.0～3.2.47 (c)Linux内核源码3.0～3.4.63(共60个版本),R2=0.986 (共160个版本),R2=0.995 (共260个版本),R2=0.955图3 Linux内核数据集实验结果

(a)4次转储数据集,R2=0.920 (b)8次转储数据集,R2=0.944 (c)12次转储数据集,R2=0.951图4 维基百科转储数据集实验结果

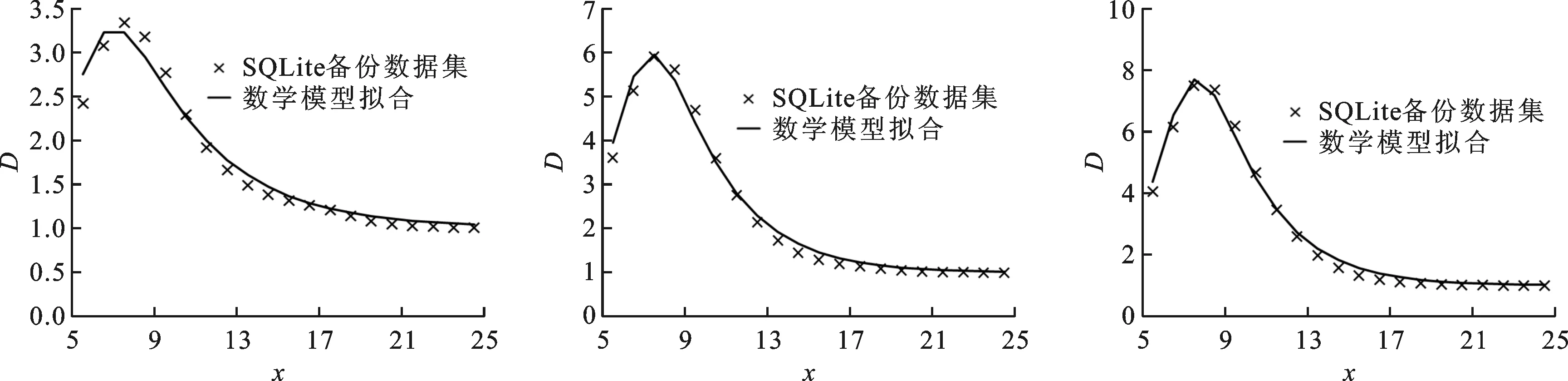
(a)10次备份数据集,R2=0.977 (b)50次备份数据集,R2=0.991 (c)90次备份数据集,R2=0.993图5 SQLite备份数据集实验结果

4 结 论

本文通过3组真实数据集Linux内核源代码、维基百科转储数据、SQLite备份数据,对目前研究者认为合理的预期分块长度值4 kB以及8 kB进行了实验验证,结果表明4 kB或者8 kB不能使基于内容分块算法的重复数据删除率最优。为了揭示预期分块长度与重复数据删除率之间隐含的数学关系,从而合理设置预期分块长度值,本文提出了一种基于Logistic函数的数学模型来描述预期分块长度与重复数据删除率之间的数学关系,并基于3组真实数据集对数学模型进行了验证。实验结果表明,反映数学模型拟合优度的R2值在0.9以上,说明所提数学模型能够准确地描述预期分块长度与重复数据删除率之间的关系。该模型为将来进一步研究能使重复数据删除率接近最优的预期分块长度设置方法奠定了理论基础。

[1] EMC. EMC data domain white paper [EB/OL]. (2014-07-01)[2016-04-20]. http: ∥www.emc.com/collateral/software/white-papers/h7219-data-domain-data-invul-arch-wp.pdf.

[2] DUBNICKI C, GRYZ L, HELDT L, et al. Hydrastor: a scalable secondary storage [C]∥Proceedings of the USENIX Conference on File and Storage Technologies. Berkeley, CA, USA: USENIX Association, 2009: 197-210.

[3] 王龙翔, 张兴军, 朱国峰, 等. 重复数据删除中的无向图遍历分组预测方法 [J]. 西安交通大学学报, 2013, 47(10): 51-56. WANG Longxiang, ZHANG Xingjun, ZHU Guofeng, et al. A grouping prediction method based on undirected graph traversal in de-duplication system [J]. Journal of Xi’an Jiaotong University, 2013, 47(10): 51-56.

[4] QUINLAN S, DORWARD S. Venti: a new approach to archival data storage [C]∥Proceedings of the First USENIX Conference on File and Storage Technologies. Berkeley, CA, USA: USENIX Association, 2002: 89-101.

[5] MIN J, YOON D, WON Y. Efficient deduplication techniques for modern backup operation [J]. IEEE Transactions on Computers, 2011, 60(6): 824-840.

[6] TSUCHIYA Y, WATANABE T. DBLK: deduplication for primary block storage [C]∥Proceedings of the Symposium on Mass Storage Systems. Piscataway, NJ, USA: IEEE, 2011: 1-5.

[7] SRINIVASAN K, BISSON T, GOODSON G, et al. iDedup: latency-aware, inline data deduplication for primary storage [C]∥Proceedings of the USENIX Conference on File and Storage Technologies. Berkeley, CA, USA: USENIX Association, 2012: 24-35.

[8] MUTHITACHAROEN A, CHEN B, MAZIERES D. A low-bandwidth network file system [C]∥Proceedings of the 18th ACM Symposium on Operating Systems Principles. New York, USA: ACM, 2001: 174-187.

[9] YOU L L, KARAMANOLIS C. Evaluation of efficient archival storage techniques [C]∥Proceedings of the 21st IEEE/12th NASA Goddard Conference on Mass Storage Systems and Technologies. Piscataway, NJ, USA: IEEE, 2004: 227-232.

[11]LILLIBRIDGE M, ESHGHI K, BHAGWAT D, et al. Sparse indexing: large scale, inline deduplication using sampling and locality [C]∥Proceedings of the USENIX Conference on File and Storage Technologies. Berkeley, CA, USA: USENIX Association, 2009: 111-123.

[12]DEBNATH B, SENGUPTA S, LI J. ChunkStash: speeding up inline storage deduplication using flash memory [C]∥Proceedings of the 2010 USENIX Conference on USENIX Annual Technical Conference. Berkeley, CA, USA: USENIX Association, 2010: 1-16.

[13]付印金, 肖侬, 刘芳, 等. 基于重复数据删除的虚拟桌面存储优化技术 [J]. 计算机研究与发展, 2012, 49(S1): 125-130. FU Yinjin, XIAO Nong, LIU Fang, et al. Deduplication based storage optimization technique for virtual desktop [J]. Journal of Computer Research and Development, 2012, 49(S1): 125-130.

[14]RABIN M O. Department of computer science: TR-15-81 [R]. Cambridge, MA, USA: Havard University, 1981.

[15]LIU A. Dedup util homepage [EB/OL]. (2010-06-07)[2016-04-20]. http: ∥sourceforge.net/projects/dedu putil/.

[16]TORVALDS L. The linux kernel archives. [EB/OL]. (2016-04-02)[2016-04-20]. http: ∥kernel.org/.

[17]WIKIPEDIA. Svwiki dump [EB/OL]. (2016-01-11)[2016-04-20]. http: ∥dumps.wikimedia.org/svwiki/.

[18]RICHARDHIPP D. SQLite homepage [EB/OL]. (2016-03-02)[2016-04-20]. http: ∥sqlite.org/.

[19]TPCC. TPC BENCHMARKTMC Standard Specification [EB/OL]. (2009-02-11)[2016-04-20]. http: ∥www.tpc.org/tpc_documents_current_versions/pdf/tpc-c_v5.11.0.pdf.

(编辑 武红江)

Influence of Expected Chunk Size on Deduplication Ratio in Content Defined Chunking Algorithm

WANG Longxiang1,DONG Xiaoshe1,ZHANG Xingjun1,WANG Yinfeng2,GONG Weifeng3,WEI Xiaolin1

(1. School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. School of Software, Shenzhen Institute of Information Technology, Shenzhen, Guangdong 518172, China;3. Inspur Group Co. Ltd., State Key Laboratory of High-End Server and Storage Technology, Jinan 250101, China)

A logistic function based mathematical model is proposed to solve the problem that, mathematical model is not used to quantitatively analyze the relationship between the expected chunk size and the deduplication ratio in the content defined chunking (CDC) based deduplication method, resulting in the difficulty in optimizing the deduplication ratio by adjusting the expected chunk size. The logistic function is used to describe the S-shaped variation trend of unique data on the basis of observation on a large number of real data sets, and the problem that the unique data is hard to be modeled by theoretical derivation is solved. It is assumed that the CDC process fits a binomial distribution, and based on the assumption two metadata models are deduced theoretically. The deduplication ratio model is finally deduced based on these two data models. Three realistic datasets are used to verify the deduplication ratio model. Experimental results show that theR2value, which denotes the goodness of fit of the model, is greater than 0.9 in most results inferring the correctness of the model. The mathematical model may facilitate the study on optimization of deduplication ratio by reasonably setting the expected chunk size.

content defined chunking; deduplication ratio; logistic function

2016-5-20。 作者简介:王龙翔(1988—),男,博士生;张兴军(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61572394);国家重点研究发展计划资助项目(2016YFB1000303);深圳市基础研究资助项目(JCYJ20120615101127404,JSGG20140519141854753)。

时间:2016-09-22

10.7652/xjtuxb201612012

TP333

A

0253-987X(2016)12-0073-06

网络出版地址:http: ∥www.cnki.net/kcms/detail/61.1069.T.20160922.1205.006.html