声子晶体板中低频完全禁带形成机理研究

李锁斌,陈天宁,奚延辉,王小鹏

(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学机械结构强度与振动国家重点实验室,710049,西安)



声子晶体板中低频完全禁带形成机理研究

李锁斌1,2,陈天宁1,2,奚延辉1,2,王小鹏1,2

(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学机械结构强度与振动国家重点实验室,710049,西安)

针对固体基局域共振型声子晶体中难以出现100 Hz以下的完全弹性波禁带问题,提出了一种新型声子晶体板,其结构由锥形复合散射体周期性阵列于一个二维二组元声子晶体板两边构成。采用有限元方法对其禁带特性和禁带形成机理进行理论研究,获得了声子晶体板中低频完全禁带的形成机理以及禁带调节规律。研究发现,不同形式的板波模态与对应的局域共振模态依据模态叠加原理相互耦合生成面内、面外两种禁带,二者叠加形成完全禁带;散射体振子的等效弹簧质量系统耦合是难以产生低频完全禁带的主要原因。研究结果表明:新型声子晶体板中散射体振子的等效弹簧质量系统可被引入的橡胶填充体解耦,致使面内、面外禁带分离;引入的锥形复合散射体可使相互分离的面内、面外禁带被同时单独调节至低频发生重叠,最终生成了一条频率范围为59～103 Hz的低频完全禁带。研究结果和结论可将声子晶体应用于工程结构低频减振中。

声子晶体板;低频完全禁带;低频禁带机理;低频减振

声子晶体是由散射体周期性排列于基体中形成的一种新型人工周期性复合材料或结构,当弹性波通过时,部分频段会被抑制,这种特性称为声子禁带[1-3]。声子禁带的存在使得声子晶体具有广泛的潜在应用价值,例如工程减振[4],因此近二十多年来对声子晶体的研究受到了广泛关注[5]。

目前,声子禁带有两种产生机理,分别为布拉格散射机理[6]和局域共振机理[7]。由布拉格散射产生的声子禁带,其波长与结构周期为同一数量级,禁带位置和带宽取决于散射体几何形状、结构对称性以及散射体与基体材料的弹性比[8-9],这便导致低频禁带需采用大尺寸结构。由局域共振产生的声子禁带,其波长比布拉格禁带低两个数量级,禁带位置和宽度主要取决于散射体的振子特性,因此突破了布拉格禁带的低频限制,可基于小尺寸来控制大波长,实现低频禁带。

由于局域共振型声子晶体中存在低频局域共振禁带,所以其有望应用于工程结构低频减振领域[10]。板结构被广泛应用于工程结构中,因此近年来对声子晶体板的研究成为热点[11-17]。弹性波在板中的传播称为兰姆波。声子晶体板有平直型和带边型两种。平直型声子晶体板由均匀板上开孔或在孔中填充散射体而形成,研究表明,此类声子晶体板较难得到低频禁带[11]。带边型结构[12]由带边(例如柱状散射体)周期性阵列于均匀基板上组成。已有学者对带边的组成材料[13]、几何形状[14-15]以及单双边布置形式[16]对禁带特性的影响分别进行了研究。另有学者将单边结构基板替换为二维二组元声子晶体板,发现其更易获得低频宽带的声子禁带[17]。

由于兰姆波主要存在面内和面外两种振动模式,分别与振子的不同局域共振模式耦合,形成面内和面外禁带。对于已提出的声子晶体板结构[11-17],在面内、面外局域共振模式的等效弹簧质量系统中,其等效刚度和等效质量均由散射体的同一物理元件提供,例如经典型声子晶体板[15],如图1所示。其中:结构元胞如图1a所示;散射体振子面内、面外局域共振模式的等效弹簧质量系统分别为K1-M1和K2-M2,如图1b所示。系统的等效刚度K1、K2由圆柱散射体A提供,等效质量M1、M2由圆柱散射体B提供,振子的等效弹簧质量系统完全耦合,进而面内、面外禁带难以被同时调节于低频处相互重叠,致使完全禁带打开位置均高于150 Hz,而工程实际中,振动频率大多低于100 Hz[18]。因此,如何通过对散射体振子的等效弹簧质量系统进行解耦,使面内、面外禁带可被单独调节至低频范围并发生重叠,进而形成一打开位置低于100 Hz的低频完全禁带,这对声子晶体应用于低频结构减振中显得尤为重要。目前,这一问题尚未得到解决。

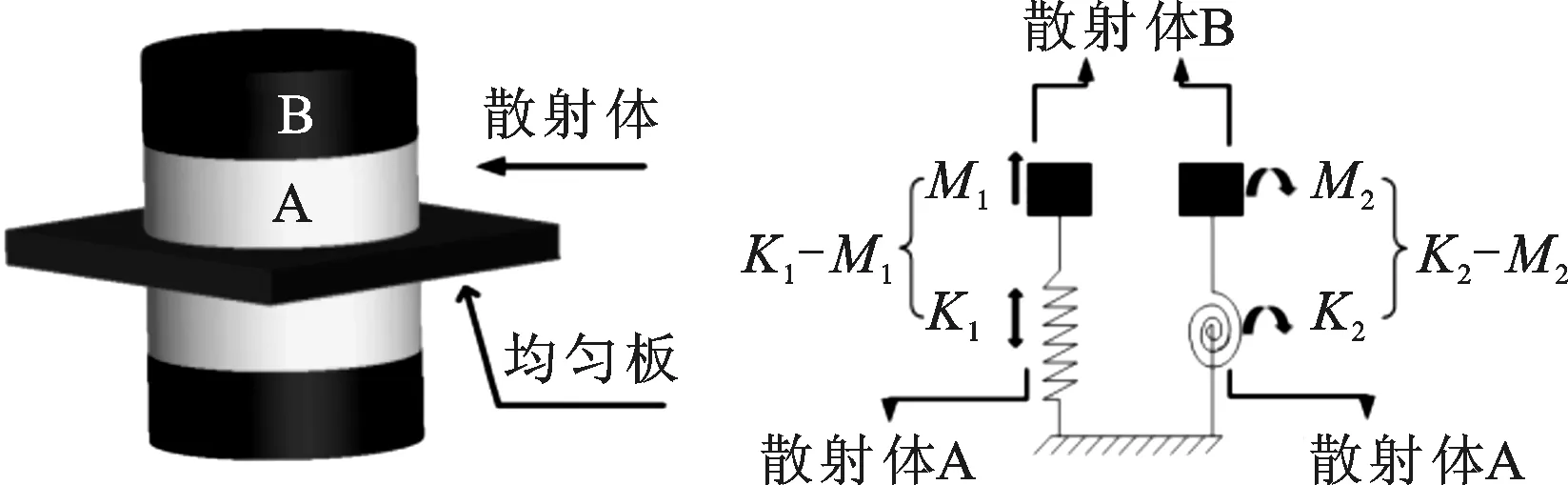
(a)晶胞单元 (b)振子等效弹簧-质量系统图1 经典型声子晶体板

将橡胶填充体和复合锥形散射体引入到经典型双边声子晶体板[15]中,构造出了一种新型声子晶体板结构,在对振子等效弹簧-质量系统解耦的基础上,可分别调节面内、面外禁带,使二者于低频处重叠,进而得到一条100Hz以下的低频完全禁带。

1 模型与计算方法

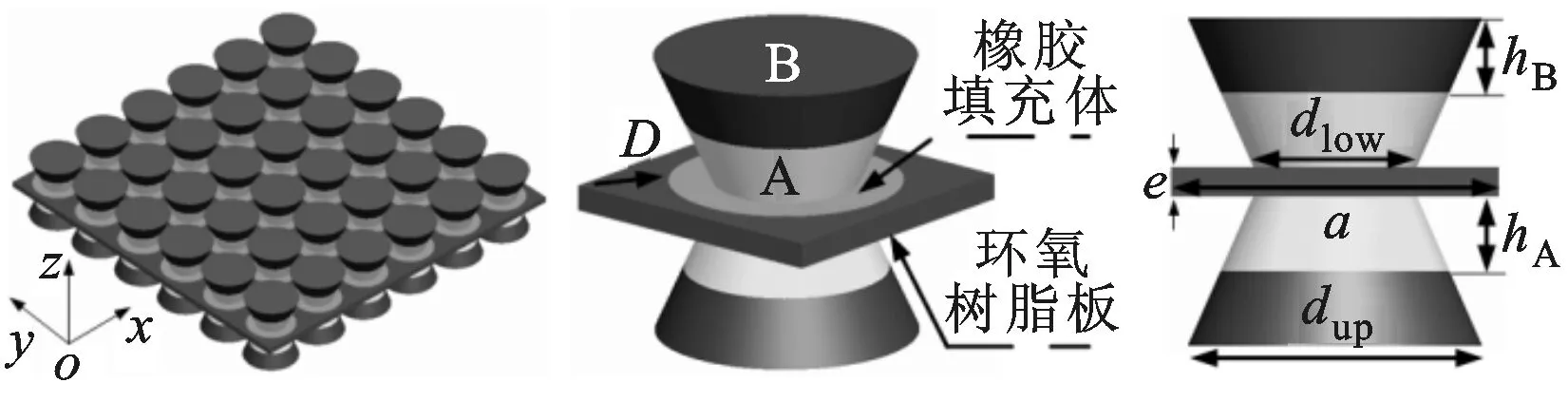
(a)部分结构 (b)晶胞单元 (c)晶胞正视图图2 新型声子晶体板结构

新型声子晶体板的具体结构如图2所示。图2a表示部分结构,由锥形复合散射体周期性阵列于一个二维二组元声子晶体板两边构成;图2b表示晶胞单元,其中锥形复合散射体单元包括A与B两部分,分别由橡胶和钢材料构成,基体单元由将橡胶材料填充于环氧树脂板孔中形成的二维二组元声子晶体板单元构成;图2c表示结构几何参数,包括晶格常数a,基板板厚e,橡胶填充体,直径为D,锥形复合散射体,底面直径为dlow、顶面直径为dup、散射体A高度为hA、散射体B高度为hB。结构材料参数见表1。

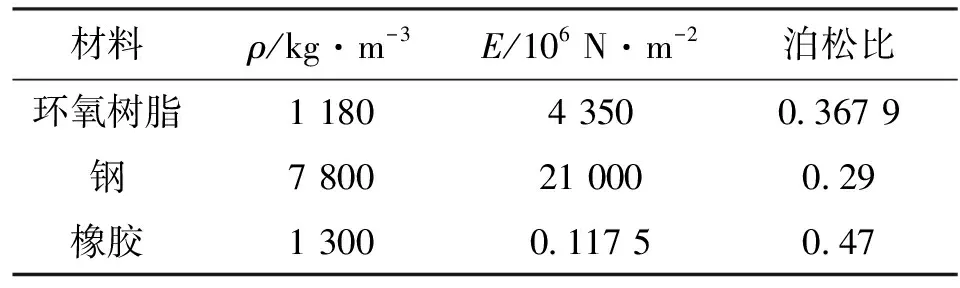
表1 结构材料参数

为了研究结构的禁带特性与形成机理,采用有限元方法计算了结构能带结果与振动模式。有限元计算采用Comsol Metaphysics 3.5a软件。基于结构周期性,以图2b所示的单个晶胞单元作为计算对象。计算过程中,z方向施加应力自由边界条件,基于布洛赫周期性条件

(1)

式中:u表示位移;x、y和z表示位置矢量;kx与ky表示第一布里渊区内周期性波矢,于x、y方向施加了周期性边界条件。波矢沿着不可约布里渊区边界点M-Γ-X-M进行扫描,求解各个波矢下结构的本征频率和对应本征模态,得到声子晶体板结构的能带结构图和单元振动模态。为了进一步证明结构能带计算结果,采用有限元方法计算了由6个元胞沿x方向组成的有限周期声子晶体板振动传输谱,结构一端施加加速度激励信号,另一端拾取加速度响应信号。通过式(2)得到有限结构的传输谱

(2)

式中:αo和αi表示输出与输入的加速度。依次改变激励频率,最终得到结构传输谱。

2 计算结果及分析

计算过程中,结构各个参数设置为D=8 mm,e=1 mm,a=10 mm,h=5 mm(hA=hB=2.5 mm),dup=9 mm,dlow=5 mm。

新型声子晶体板能带结果如图3所示。在频率0～400 Hz范围内,存在14条能带,分别为板波模式能带和由振子局域共振产生的平直模式能带。其中:板波模式包括以对称兰姆波模式为主的面内模式(如图3a中能带S2、S4)和以非对称兰姆波模式为主的面外模式(如图3a中能带A2);平直模式能带包括与板波模式发生耦合的平直模式能带(如图3a中能带S1、S3、A1)和不能与板波模式发生耦合的平直模式能带(如图3a中能带f4)。两种模式耦合形成对应的面内和面外禁带,两种禁带相互重叠形成完全禁带。

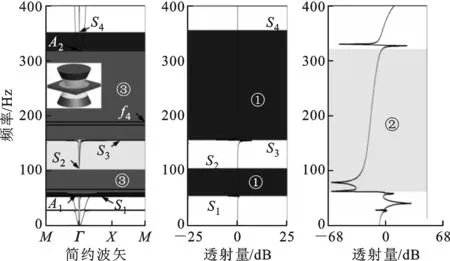
(a)能带 (b)面内传输谱 (c)面外传输谱图3 新型声子晶体板能带图及透射谱

图3中包含2条面内禁带(图3b中①号区域表示),1条面外禁带(图3c中②号区域表示)和由二者重叠形成的2条完全禁带(图3a中③号区域表示)。第1条面内禁带由面内模式S2与对应的平直模式S1耦合而成,禁带范围为53～103 Hz,绝对带宽为50 Hz;第2条面内禁带由面内模式S4与对应的平直模式S3耦合而成,禁带范围为154～352 Hz,绝对带宽为198 Hz;1条面外禁带由面外模式A2与对应的平直模式A1耦合而成,禁带范围为59～318 Hz,绝对带宽为259 Hz;第1条完全禁带由第1条面内禁带与第1条面外禁带重叠而成,禁带范围为59～103 Hz;第2条完全禁带由第2条面内禁带与第1条面外禁带重叠而成,禁带范围为154～318 Hz。带宽用绝对带宽与禁带中心位置之比得到的相对带宽表示,对应的第1、2条完全禁带相对带宽分别为54%和69%。为了进一步验证能带计算结果,分别计算了结构面内和面外振动传输谱,结果分别如图3b和图3c所示。可以看出,禁带范围内均出现了弹性波的衰减,进而验证了能带计算结果。为了比较,进一步计算了经典型声子晶体板[15]和由通过引入锥形复合散射体形成的过渡型声子晶体板的能带结构,结果分别如图4、图5所示。在0～800 Hz频率范围内,二者均只有一条完全禁带出现,其频率范围分别为217～405 Hz和321～469 Hz,禁带起始位置均高于100 Hz。

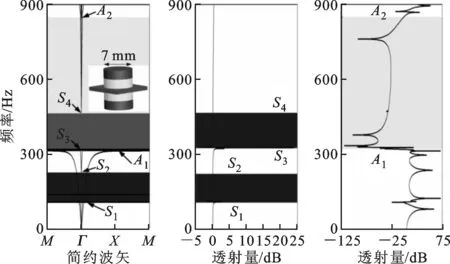
(a)能带 (b)面内传输谱 (c)面外传输谱图4 经典型声子晶体板能带图及透射谱

(a)能带 (b)面内传输谱 (c)面外传输谱图5 过渡型声子晶体板能带图及透射谱

比较3种结构能带结果可以发现:经典型声子晶体板在引入双边锥形复合散射体后,其面内、面外禁带均移向低频,但完全禁带仍由第2条面内禁带与第1条面外禁带叠加而成;进一步引入橡胶填充体后,第1条面外禁带继续向低频移动,最终与第1条面内禁带重叠,进而产生一条低于100Hz的低频完全禁带。

3 低频完全禁带形成机理

为了进一步探讨新型声子晶体板中低频完全禁带形成机理,分别提取了3种声子晶体板能带结构中第1条面外、面内禁带上下边界对应的单元振动模式A1、S1和A2、S2。

(a)新型结构 (b)过渡型结构 (c)经典型结构图6 单元面外振动模式

3种声子晶体板面外禁带上下边界对应的单元振动模式位移云图如图6所示,图中A1为单元局域共振模式,对应禁带下边界;A2为单元面外振动模式,对应禁带上边界。当面外波激励时,模式A2激活后放大成为主模态,此时基板沿z方向运动,而散射体基本保持静止,因此面外波可通过基板面外振动模式在声子晶体板中传播;当激励频率接近散射体振子固有频率时,模式A1激活后放大转换为主模态,此时振子沿z方向且通过橡胶填充体给基板一个作用力,其大小正比于振子振幅(约正比于放大因子)、橡胶填充体刚度,进而阻止了基板沿z方向运动,抑制了基板面外振动模式,致使面外波无法在声子晶体板中传播,第1条面外禁带打开;在面外禁带内(平直能带A1上方区域),局域共振模式A1始终保持为主模态,反作用力持续作用于基板上,基板面外振动模式继续被抑制。依据模态叠加原理[19]

(3)

式中:x表示响应;ηAn表示模式An的参与因子。当激励频率逐渐远离振子固有频率时,模式A1的放大因子逐渐变小,其参与因子ηA1变小,振子振幅随之减弱,致使作用于基板上的反作用力逐渐变小,最终消失,此时第一面外禁带关闭。该形成原理可视化过程如图7所示,共包含4个过程。当有限结构基板右端激励频率接近振子固有频率时,参与因子ηA1约等于放大因子,此时模式A1激活后放大成为主模态,致使波传播被抑制,即结构左端基板保持静止,如图7过程1所示;当波激励频率逐渐远离振子固有频率时,放大因子变小而导致参与因子ηA1逐渐变小,此时模式A2转换为主模态,致使激励被传播,即结构右端基板末端出现微幅运动,如图7过程4所示。

图7 禁带形成过程机理

面外禁带打开位置由局域共振模式A1的固有频率决定,模式A1的振动过程可理解为一等效弹簧-质量系统(K1-M1),其固有频率由下式确定

(4)

式中:K1表示系统刚度(压缩或拉伸);M1表示系统集中质量。对于经典型和过渡型声子晶体板,系统刚度K1由单个散射体A提供,系统集中质量M1由单个散射体B提供。相比柱形散射体,锥形散射体的等效刚度较小,但系统等效质量M1保持不变,于是过渡型声子晶体板面外禁带可被调节至低频;对于新型声子晶体板,散射体沿z方向做整体运动,同时受橡胶填充体约束,且固有频率不为0,依据振动力学中的刚体模态概念,将散射体的这种振动模式命名为“类刚体模态”,此时系统集中质量M1由整个散射体提供而变大,系统等效刚度K1由橡胶填充体提供,于是该型板的面外禁带可调节至更低频。

(a)新型结构 (b)过渡型结构 (c)经典型结构图8 面内振动模式

(5)

式中:ηSn表示模式Sn的参与因子。当激励频率逐渐远离振子固有频率时,模式S1的放大因子逐渐变小,导致参与因子ηS1变小,振子振幅随之减弱,致使作用于基板上的反作用力逐渐减小,最终消失,第一面外禁带关闭。

禁带打开位置由单元共振模式S1决定,其振动过程可理解为一等效弹簧-质量系统(K2-M2)。对于3种声子晶体板,系统等效刚度K1均由单个散射体A提供,等效质量M2均由单个散射体B提供。由于锥形散射体等效刚度小于柱形散射体,因此可将面内带隙调节至低频。

从以上分析可以得出,对于带边型声子晶体板,其散射体振子的等效弹簧质量系统包含K1-M1与K2-M2这2个子系统。子系统K1-M1中特定的局域共振模式与反对称兰姆波振动模式依据模态叠加原理耦合产生面外禁带;子系统K2-M2中特定的局域共振模式与对称兰姆波振动模式依据模态叠加原理耦合产生面内禁带;禁带打开位置取决于子系统固有频率。

相对子系统K1-M1与K2-M2相互耦合的经典型声子晶体板,在新型声子晶体板中,橡胶填充体的引入使得子系统K1-M1与K2-M2相互解耦,如图9所示。系统中等效刚度K1由橡胶填充体提供,K2由散射体A提供,等效质量M1由整个散射体提供,M2由散射体B提供,于是面内、面外禁带可被单独调节;同时,“类刚体模态”形成,系统等效质量M1增大,等效刚度K1减小,于是将面外禁带调至低频;锥形散射体引入,使得等效刚度K2减小,于是将面内禁带调至低频;最终,面内面外禁带在低频处发生相互重叠,进而产生了一条低于100 Hz的完全禁带。

图9 新型结构散射体振子的等效弹簧-质量系统

4 散射体参数对低频禁带影响规律

由上述分析可知,锥形复合散射体可同时影响“类刚体模态”的集中质量M1和面内振动模式的等效刚度K2,因此,锥形复合散体为调节禁带的主要因素,于是将进一步研究锥形复合散射体对面内、面外禁带的影响规律。以散射体B的高度hB为影响参数,研究锥形复合散射体对面内、面外禁带的影响规律。

4.1 散射体B高度对面外禁带的影响规律

当散射体B高度hB从0逐渐变化为5 mm时,面外禁带的变化规律如图10所示。可以看出,随着高度hB增大,面外带隙打开位置逐渐移向低频(从118 Hz降到51 Hz),同时带宽逐渐变宽。

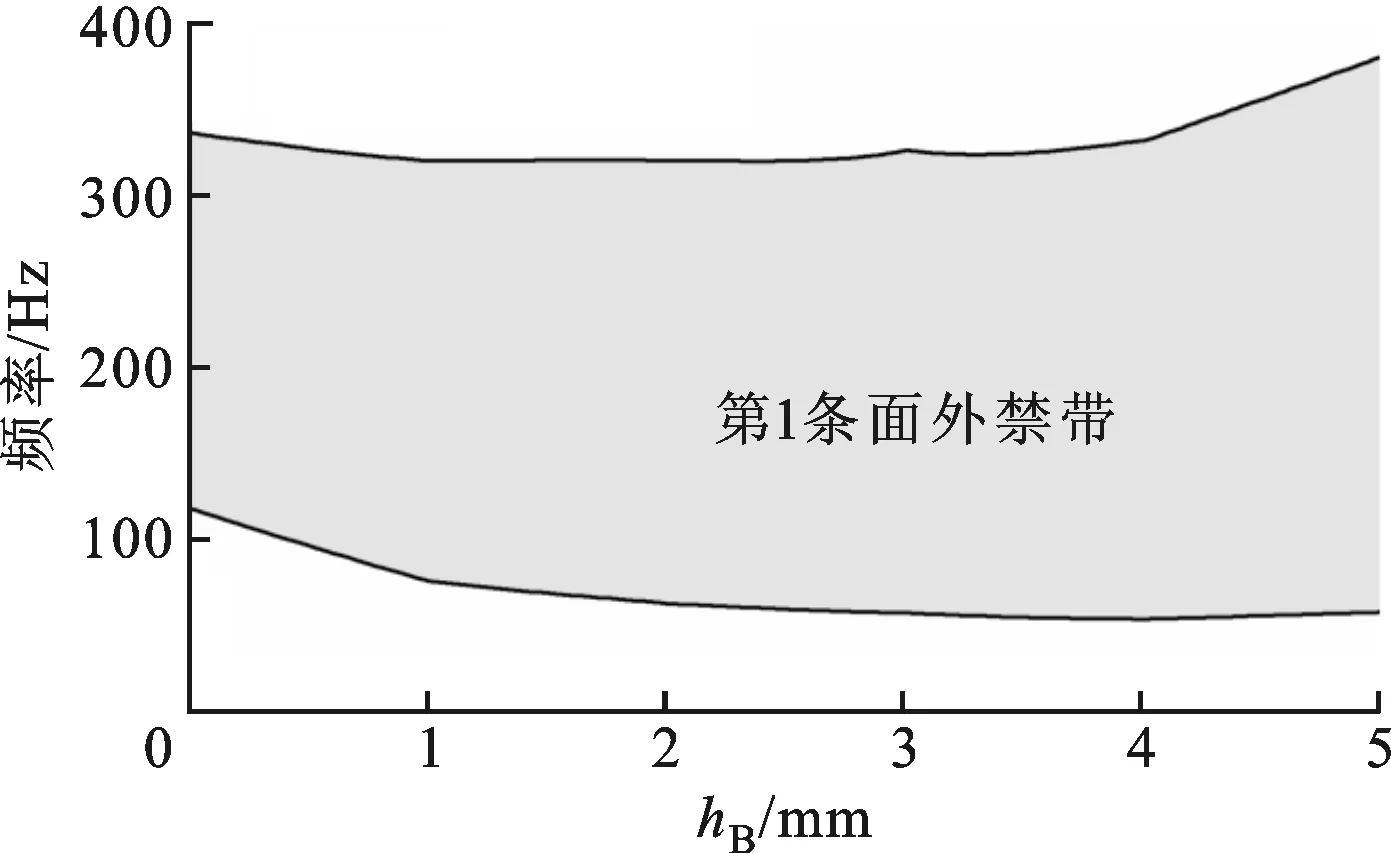
图10 散射体B高度对面外禁带的影响规律

由低频禁带形成机理可知,面外禁带打开位置由子系统K1-M1的固有频率决定,固有频率大小主要由“类刚体模态”确定,当hB逐渐增大时,“类刚体模态”的等效质量M1逐渐增大,等效刚度K1保持不变,于是子系统K1-M1固有频率减小,面外禁带移向低频。其可视化机理如图11所示。

目前，民富社区腰鼓队有33名队员，全部是辖区的退休人员。9月14日上午，民富社区活动室，记者看到腰鼓队队员正挥舞着鼓棒，个个英姿飒爽、精神抖擞地在练习腰鼓。

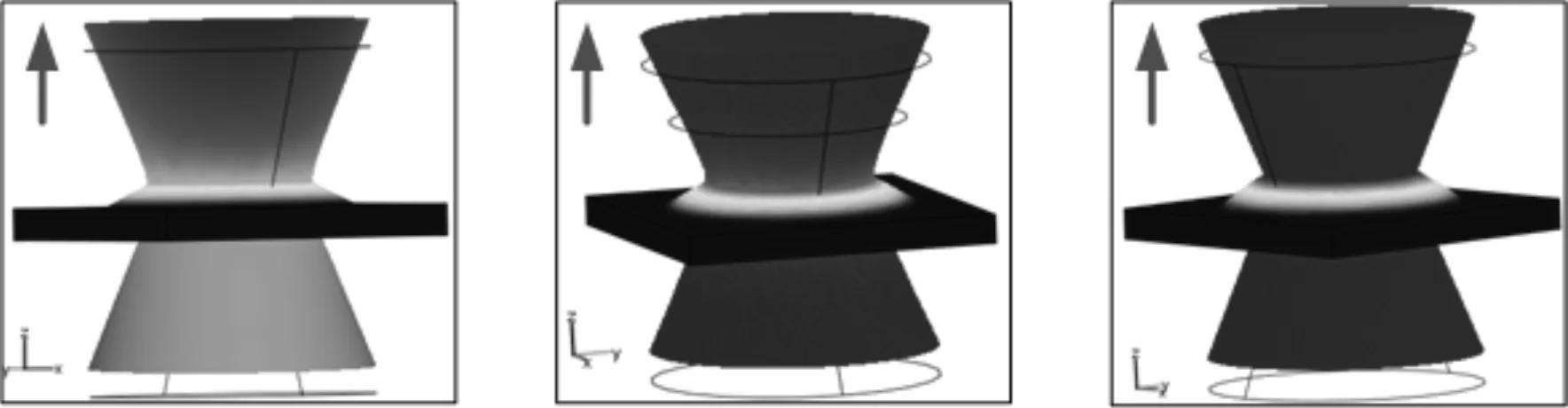
(a)hB=0 (b)hB=2 mm (c)hB=5 mm图11 面内局域振动模式(类刚体模态)随hB的变化规律

此过程中,由于双边的引入,散射体的“类刚体模态”与板波振动模式的耦合随着hB的增大而增大,导致禁带变宽。

4.2 散射体B高度对面内禁带的影响规律

当散射体B高度hB从0逐渐变为5 mm时,第1、2条面内禁带的变化规律如图12所示。可以看出,随着hB增大,二者先向低频移动,之后又移向高频,同时禁带逐渐变宽。

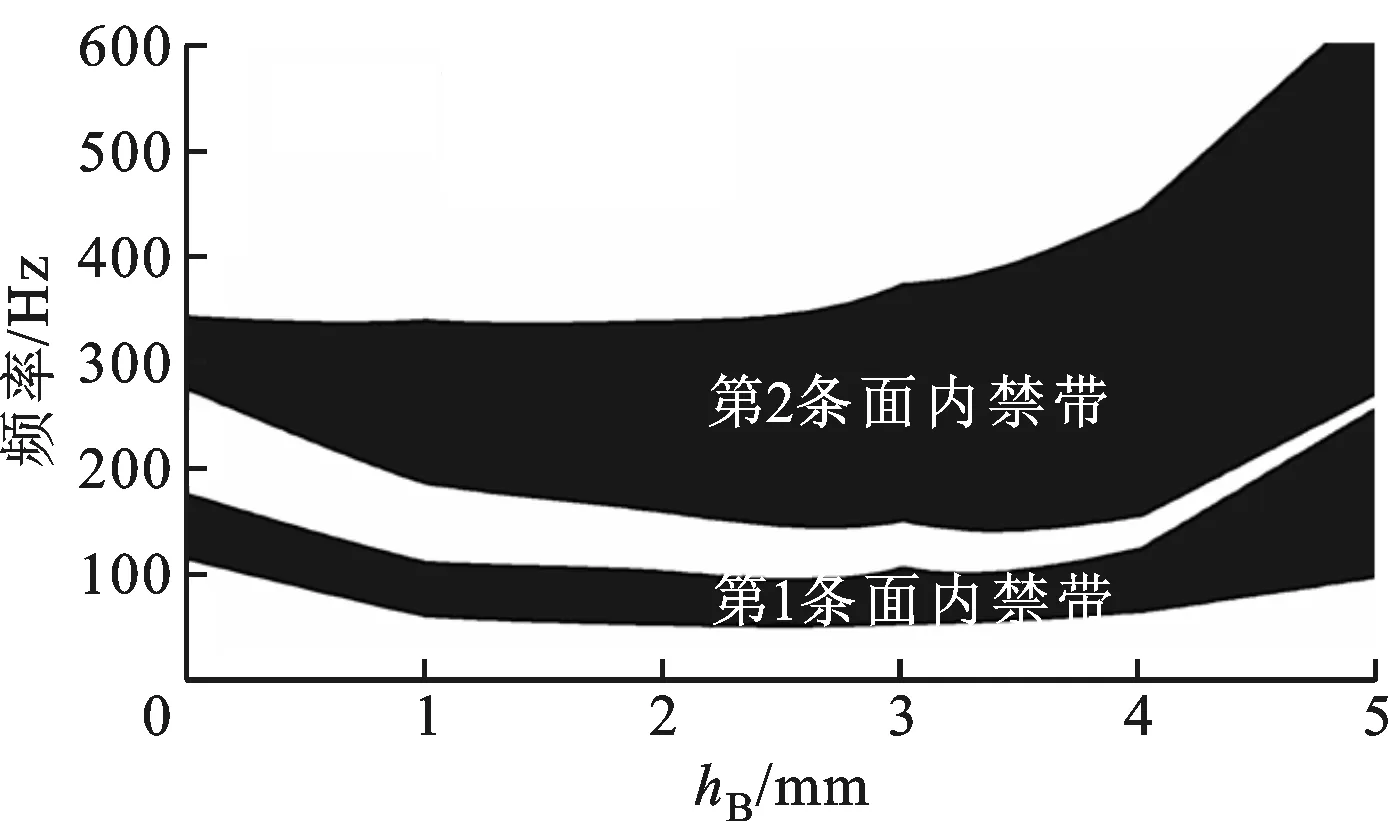
图12 散射体B高度对面内禁带的影响规律

由低频禁带形成机理可知,面内禁带打开位置由子系统K2-M2的固有频率决定,当hB开始增大(不大于4 mm)时,等效刚度K2减小,等效质量M2增大,子系统K2-M2的固有频率减小,面内禁带移向低频;当hB进一步增大(大于4 mm)时,沿xy平面出现“类刚体模态”,此时橡胶填充体替代散射体A成为子系统K2-M2的等效刚度,其大小等于橡胶填充体的横向刚度,致使K2变大,其增幅大于M2,进而导致子系统K2-M2的固有频率增大,面内带隙移向高频。其可视化机理如图13所示。

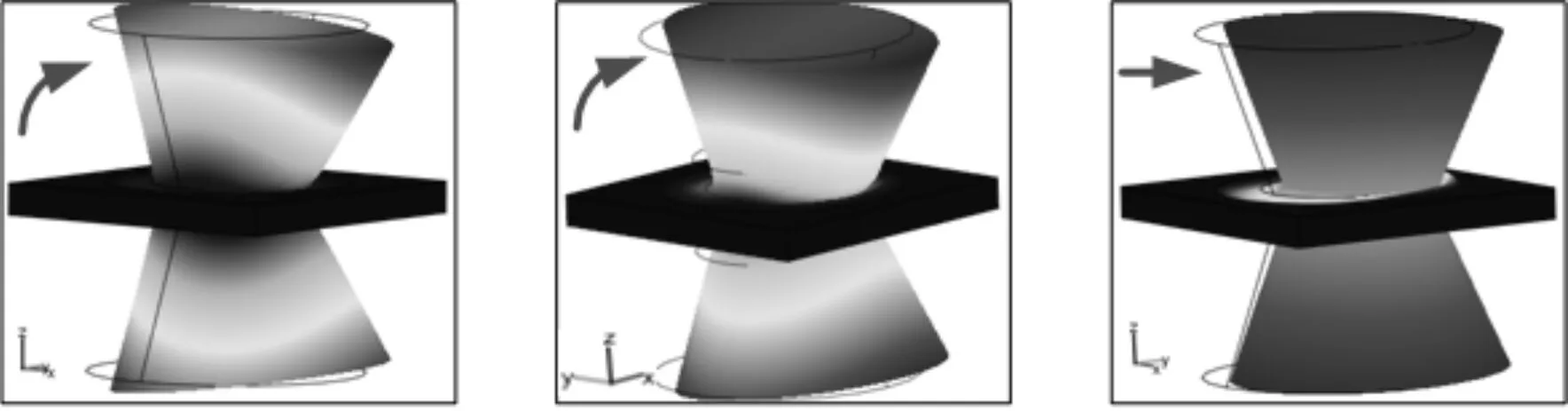
(a)hB=0 (b)hB=4 mm (c)hB=5 mm图13 面内局域振动模式随散射体B高度hB的变化规律

此过程中,由于双边的引入,局域共振模式与兰姆波模式的耦合随着hB的增大逐渐增大,导致禁带变宽。

5 结 论

在分析传统型声子晶体板结构特性的基础上,提出了一种新型声子晶体板结构,通过对其禁带特性的研究,最终提出了声子晶体板中低频完全禁带的形成机理和禁带调节规律,并得出如下结论。

(1)低频完全弹性波禁带的频率范围为59～103 Hz。

(2)研究发现,系统主振型在局域共振模式与板波振动模式二者间的相互切换决定着禁带的打开与关闭。

(3)新结构中通过引入橡胶填充体解耦了振子的等效弹簧-质量系统,进而实现了对面内、面外禁带进行单独调节;形成的“类刚体模态”可将面外禁带单独调节至低频。进一步引入双边复合锥形散射体,可将面内禁带调节至低频。最终,面内、面外禁带相互重叠,产生了一条低于100 Hz的完全禁带。

(4)复合锥形散射体可同时影响“类刚体模态”和面内振动模式,通过调节散射体参数可对结构低频完全禁带进行调节。

研究结果表明,声子晶体可应用于工程结构低频减振领域,研究结论可为得到低频完全禁带提供理论参考。

[1] SIGALAS M, ECONOMOU E N. Elastic and acoustic wave band structure [J]. Journal of Sound and Vibration, 1992, 158(2): 377-382.

[2] SIGALAS M, ECONOMOU E N. Band structure of elastic waves in two dimensional systems [J]. Solid State Commun, 1993, 86(3): 141-143.

[3] 温熙森, 温激鸿, 郁殿龙, 等, 声子晶体 [M]. 北京: 国防工业出版社, 2009: 1-30.

[4] LI Xiaochun, LIU Zhengyou. Coupling of cavity modes and guiding modes in two-dimensional phononic crystals [J]. Solid State Commun, 2005, 133(5): 397.

[5] LI Fengming, WANG Yize. Elastic wave propagation and localization in band gap materials: a review [J]. Science China, 2012, 55(10): 1734-1746.

[6] KUSHWAHA M S, HALEVI P, DOBRZYNSKI L, et al. Acoustic band structure of periodic elastic composites [J]. Physical Review Letters, 1993, 71(13): 2022-2025.

[7] LIU Zhengyou, ZHANG Xixiang, MAO Yiwei, et al. Locally resonant sonic materials [J]. Science, 2000, 289(5485): 1734-1736.

[8] GORISHNYY T, ULLAL C K, MALDOVAN M, et al. Hypersonic phononic crystals [J]. Physical Review Letters, 2005, 94(11): 3035.

[9] ZHOU Xiaozhou, WANG Yuesheng, ZHANG Chuanzeng. Effects of material parameters on elastic band gaps of two-dimensional solid phononic crystals [J]. Journal of Applied Physics, 2009, 106(1): 014903.

[10]HO K M, CHENG C K. YANG Z, et al. Broadband locally resonant sonic shields [J]. Applied Physics Letters, 2003, 83(26): 5566-5568.

[11]CHEN J J, HAN X, LI G Y. Asymmetric Lamb wave propagation in phononic crystal slabs with graded grating [J]. Journal of Applied Physics, 2013, 113(18): 184506.

[12]WU T T, HUANH Z G, TSAI T C, et al. Evidence of complete band gap and resonances in a plate with periodic stubbed surface [J]. Applied Physics Letters, 2008, 93(11): 111902.

[13]PENNEC Y, DJAFARI-ROUHANI B, LARAB I, et al. Low-frequency gaps in a phononic crystal constituted of cylindrical dots deposited on a thin [J]. Physical Review: B, 2008, 78(78): 104105.

[14]HSU J. Local resonances-induced low-frequency band gaps in two-dimensional phononic crystals slabs with periodic stepped resonators [J]. Journal of Physics: D Applied Physics, 2011, 44(5): 55401-55409.

[15]ZHANG Siwen, WU Jiuhui, HU Zhiping. Low-frequency locally resonant band-gaps in phononic crystal plates with periodic spiral resonators [J]. Journal of Applied Physics, 2013, 113(113): 163511.

[16]ASSOUAR M B, OUDICH M. Enlargement of a locally resonant sonic band gap by using double-sides stubbed plate [J]. Applied Physics Letters, 2012, 100(12): 123506.

[17]LI Yinggang, CHEN Tianning, WANG Xiaopeng, et al. Enlargement of locally resonant sonic band gap by using composite plate-type acoustic metamaterial [J]. Physicals Letters A, 2015, 379(5): 412-416.

[18]ROUNDY S. On the Effectiveness of vibration-based energy harvesting [J]. Journal of Intelligent Material Systems and Structures, 2005, 16(16): 809-823.

[19]THOMSON W T, DAHLEH M D. Theory of vibration with applications [M]. Beijing: Tsinghua University Press, 2005: 81-82.

[本刊相关文献链接]

张凯,陈天宁,王小鹏.非阻塞性颗粒阻尼器内部的颗粒莱顿弗罗斯特现象.2016,50(8):15-19.[doi:10.7652/xjtuxb 201608003]

蔺彦虎,赵宁,彭艳军.具有循环对称特点的耦合结构振动特性分析.2016,50(7):68-74.[doi:10.7652/xjtuxb201607011]

周建星,孙文磊,曹莉,等.行星齿轮传动系统碰撞振动特性研究.2016,50(3):16-21.[doi:10.7652/xjtuxb201603003]

刘雅琳,上官博,徐自力.干摩擦阻尼对失谐叶盘系统受迫振动的影响.2016,50(2):111-117.[doi:10.7652/xjtuxb2016 02019]

郭涛,管志成,孙光普,等.调频振子-液体联合水平减振的流固耦合机理研究.2016,50(1):28-33.[doi:10.7652/xjtuxb 201601005]

权双璐,刘杰,韩罗峰,等.一种机械系统非线性类别辨识方法.2015,49(12):104-111.[doi:10.7652/xjtuxb201512017]

郭涛,李国君.内嵌晃荡液体减振的流固耦合分析.2014,48(9):117-122.[doi:10.7652/xjtuxb201409020]

毛阳,陈志勇,史文库,等.磁流变液双质量飞轮扭振减振特性研究.2014,48(6):127-133.[doi:10.7652/xjtuxb201406 022]

张超,陈天宁,王小鹏,等.颗粒阻尼线性离散元模型参数的选取方法.2014,48(3):96-101.[doi:10.7652/xjtuxb201403 018]

(编辑 武红江)

Forming Mechanisms of Low-Frequency Complete Band Gaps in Phononic Crystal Plate

LI Suobin1,2,CHEN Tianning1,2,XI Yanhui1,2,WANG Xiaopeng1,2

(1. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049, China)

A novel phononic crystal plate is proposed to obtain a complete band gap below 100 Hz for the application of localized resonance phononic crystals (LRPCs) to the reduction of low-frequency vibration control in engineering. The structure of the plate is composed of double-sided taper composite stubs which are deposited on a 2D locally resonant PC plate, and its theoretical properties are studied. The dispersion relationship, the power transmission spectrum and the displacement fields of the eigenmode are calculated using a finite element method. It is shown that the coupling between the local resonance mode and the Lamb wave mode follows the modal superposition principle and is responsible for the formation of the band gaps. Moreover, the spring-mass system of the resonator is decoupled by introducing the rubber filler, and then the out-of-plane band gap and the in-plane band gap are adjusted into the same lowest frequency range respectively. As a result, the frequency range of the generated complete band gap is between 59 Hz and 103 Hz due to the overlap between the in-plane and out-of-plane band gaps. This study provides an effective way for phononic crystals to obtain complete band gaps in low-frequency range (below 100 Hz), and has potential application to the reduction of low frequency vibration.

phononic crystal plate; low-frequency complete band gap; forming mechanism of lower-frequency band gap; vibration reduction

2016-05-26。 作者简介:李锁斌(1984—),男,博士生;陈天宁(通信作者),男,教授,博士生导师。 基金项目:长江学者和创新研究团队发展计划资助项目(IRT1172);国家自然科学基金资助项目(51275377)。

时间:2016-10-19

10.7652/xjtuxb201612009

O799

A

0253-987X(2016)12-0051-07

网络出版地址:http: ∥www.cnki.net/kcms/detail/61.1069.T.20161019.1112.002.html