一种提高异步电动机转矩性能的直接转矩控制方法

刘小勇,郑爱红,蒋峰,昝鑫,曹建福

(西安交通大学电子与信息工程学院,710049,西安)



一种提高异步电动机转矩性能的直接转矩控制方法

刘小勇,郑爱红,蒋峰,昝鑫,曹建福

(西安交通大学电子与信息工程学院,710049,西安)

针对传统异步电动机直接转矩控制方法中存在的磁链控制不对称和转矩脉动较大的问题,提出了一种优化的异步电动机直接转矩控制方法。该方法通过重新划分电压矢量对定子磁链和电磁转矩作用的影响范围,改进了电压矢量选择表,使转矩和磁链变化时能正确选择所需电压矢量,以减小转矩脉动,从而避免了传统直接转矩控制方法在选取电压矢量时,忽略转矩增加的必要条件和磁链变化的临界条件的问题;通过求解转矩脉动公式,推导出最佳转矩误差值,提出了转矩脉动全局最小条件下的占空比计算方法,进一步优化了转矩性能,并给出了定子磁链和电磁转矩的控制推导公式。仿真及实验结果表明,所提方法比传统直接转矩控制策略的系统动态响应速度提高了约30%,同时转矩及电流脉动减小,磁链控制更接近圆形轨迹,具有工程实用价值。

异步电动机;直接转矩控制;转矩脉动;电压矢量;占空比

直接转矩控制(DTC)技术在发展过程中不断地进行优化和提高,但还没有完善,其显著的缺点是转矩波动较大、低速控制性能较差,制约了其在高性能调速领域的应用。

DTC方法摒弃了矢量控制中解耦的思想,根据定子磁链的位置、定子磁链和转矩的误差,采用滞环比较器和开关逻辑表,直接生成作用于电机的定子电压矢量,以驱动电机。DTC方法因其具有对电机模型参数依赖程度小的优点,已成为交流传动的新热点,但它的缺点是转矩脉动较大、开关频率不固定等[1]。为了克服传统DTC方法的缺点,已提出了很多方法,包括空间矢量调制(SVW)技术[2-3]、转矩脉动最小化方法[4-5]、模糊逻辑自适应方法[6]、在一个周期使转矩平均与参考值逼近方法[7]等,但这些方法依赖多项电机参数,很难在实际中应用。

在DTC方法中,定子电压矢量用于驱动电机,决定着转矩和磁链轨迹的变化,所以其选择表尤为重要。传统的DTC方法在考虑定子电阻压降的影响时,其区间的电压选择不精确,且当定子磁链处于区段线附近时控制性能变差[8]。文献[9]对此进行了一些探讨,提出实际应用中应考虑定子电阻压降的影响。本文在此基础上分析了电压矢量对磁链和转矩的影响,进一步提出转矩增加的前提条件和磁链变化的临界条件,从而优化了电压矢量选择表,使转矩和磁链变化时能正确选择所需电压矢量,以减小转矩脉动;同时根据转矩脉动公式,推导出最佳转矩误差值,得到在转矩脉动全局最小条件下的占空比计算方法。仿真与实验证明了理论分析的正确性和有效性,在加快系统响应的同时减小了转矩和电流脉动,改善了调速性能。

1 直接转矩控制原理

直接转矩控制技术是将电机与逆变器作为一个整体,在定子坐标系下,利用空间电压矢量分析法观测磁链和转矩值,综合定子磁链的位置、定子磁链和转矩的误差,通过滞环比较器和开关逻辑表,直接生成系统所需的瞬时定子电压矢量,来控制定子磁链的运动,以迅速改变负载角,实现对转矩的直接控制。

us为定子电压空间矢量;is为定子电流空间矢量;ir为转子电流空间矢量;Ψs为定子磁链空间矢量;Ψr为转子磁链空间矢量;Rs为定子电阻;Rr为转子电阻;Ll为漏电感;L为主电感;ω为角速度图1 异步电动机的空间矢量等效电路图

运用直接转矩控制对异步电动机进行控制,其空间矢量等效图[10]如图1所示。首先分析异步电动机的数学模型,异步电动机定子方程为

(1)

转子方程为

(2)

磁链方程为

(3)

(4)

转矩方程为

(5)

或

(6)

式中:D为微分符号;np是电机极对数;θ是磁通角(rad)。

电机运动方程

(7)

式中:TL为负载转矩;J为转动惯量。

由式6可见,正确控制磁链是转矩控制的关键,下面分析电压矢量如何作用于磁链和转矩。

2 电压矢量对磁链和转矩作用范围

根据式(5),施加不同的电压矢量,对磁链和转矩产生的作用是不同的,力矩在定子侧可表示为

(8)

两边求导并同时乘以Ll得到

(9)

根据图1可知

(10)

结合式(10)以及式(2)、(4),可推导出

(11)

磁链与电压、电流的关系式为

(12)

将式(11)、(12)代入式(9),得

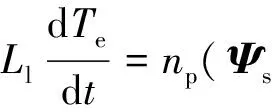
(13)

式中:Rm=((1+Ll/L)Rs+Rr。

根据式(13),当转矩增加时,即dTe/dt>0,

np|Ψs||us|sinθ2>npωΨs·Ψr+RmTe

(14)

在直接转矩控制中,对电流进行限制的情况下,转子磁链与定子磁链很接近,在负载不超过额定负载很多时,可以认为Ψs≈Ψr[9],那么,式(13)近似为

即当Ψs和us的夹角大于θ2时,才能使转矩增加。θ2可表示为

(15)

由定子电压式(1)可知

(16)

式中:Es为定子反电势矢量。

定子电压矢量和反电势矢量的夹角θ1为

(17)

根据式(16),ΔΨs和Es的方向一致,即定子电压矢量与ΔΨs的夹角为θ1。当电压矢量与磁链夹角为(90°-θ1)时,考虑定子电阻压降的影响,此时实际的ΔΨs与磁链夹角为90°,如图2所示,由于Ψs+1=Ψs+ΔΨs,因此此时得到的磁链Ψs+1幅值(为三角形的斜边)最大。文献[7]以此刻为影响范围的临界划分点,应当以|Ψs+1|=|Ψs|时,电压矢量与磁链所成夹角为划分点。

图2 电压矢量与磁链夹角为90°-θ1时的各矢量关系图

|Ψs+1|=|Ψs|时的矢量图如图3所示,设此时ΔΨs与Ψs的夹角为θ3,即Es与Ψs的夹角为θ3,电压矢量us与Ψs的夹角为(θ3-θ1),根据余弦定理,可得

(18)

(19)

其余3个象限夹角范围的临界划分与第一象限的分析相同。综合θ1、θ2、θ3的影响,可得改进的电压矢量对定子磁链和转矩的影响范围如图4和表1所示。

图3 |Ψs+1|=|Ψs|时定子磁链空间矢量关系图

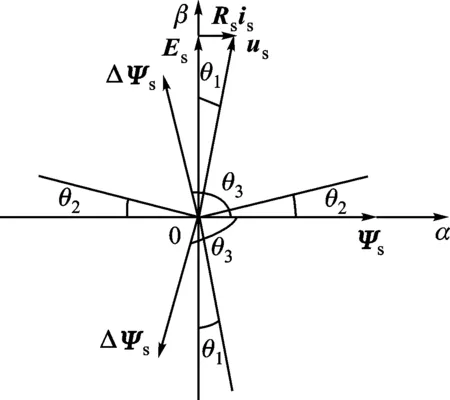
图4 改进的电压矢量对定子磁链和转矩的影响范围

电压矢量与磁链的夹角范围电压矢量对磁链的作用电压矢量对转矩的作用θ2～θ3-θ1增大增大θ3-θ1～180°-θ2减小增大180°-θ2～360°-θ3-θ1减小减小360°-θ3-θ1～360°+θ2增大减小

3 改进的电压矢量选择表

12区段磁链闭环直接转矩控制是将传统的6区段再划分,每区段为30°,并且以(-15°,15°)为第1区段,用S1表示,控制定子磁链按逆时针方向旋转。采用12区段(S1～S12)控制,增加和减小磁链的两电压矢量对磁链幅值的影响是比较对称的,可大大减小转矩的脉动[11]。根据以上电压矢量对磁链和转矩的影响,可以分析出12区段的电压矢量选择表,如表2所示,磁链和转矩调节器都采用双位调节器,Ψ和τ分别表示磁链和转矩调节器的输出。Ψ=0表示要减小磁链,Ψ=1表示要增加磁链,τ=0表示要减小转矩,τ=1表示要增加转矩。

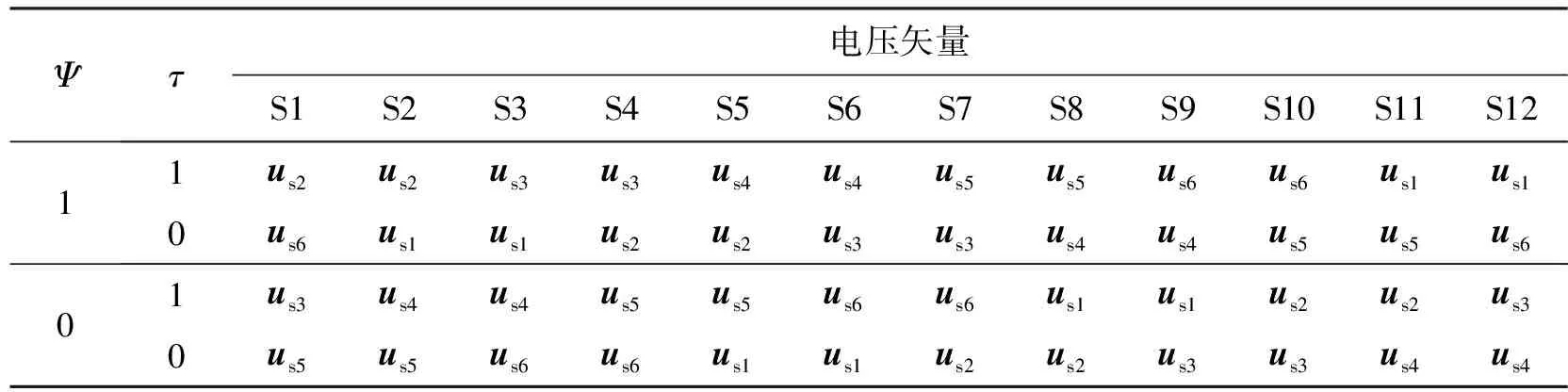
表2 改进的12区段直接转矩控制电压矢量选择表

4 优化的占空比计算方法

以定子和转子磁链矢量为状态变量的异步电动机的状态变量形式为

(20)

式中:σ为电机漏磁系数。电磁转矩为

(21)

在一个控制周期tsp内,定子和转子的磁链在(k+1)采样点可表示为

(22)

(23)

将式(22)、(23)代入式(21)的离散形式,通过施加一个非零电压矢量,转矩在(k+1)时刻的增量为

(24)

式中

(25)

同理,在一个周期tsp内,通过施加一个零电压矢量,转矩在(k+1)时刻的减小量为

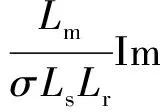
(26)

式中

(27)

那么转矩脉动误差可以表示为

(28)

在一个控制周期tsp内,若非零矢量usk和零矢量u0分别作用的时间为ts和(tsp-ts),那么

(29)

电压矢量usk作用的最优时间满足以下方程

(30)

解方程(30),可以得到

(31)

注意到转矩脉动方程(29)也是关于转矩误差初始值的方程,那么必定存在一个最佳转矩误差初始值Terror_t0(opt)满足以下方程

(32)

解方程(32),可得

(33)

占空比如下

(34)

(35)

式(35)是通过最佳转矩误差计算所得,满足转矩脉动全局最小条件,保证了系统的转矩性能。

5 仿真和结果分析

5.1 仿真结果分析

在Matlab/Simulink的环境下,建立异步电动机的直接转矩控制系统模型。在相同的条件下,将传统DCT方法和本文提出的改进方法进行了仿真对比。采用的异步电动机参数:功率为15 kW,额定电压为400 V,额定频率为50 Hz,额定转速为1 460 r/min,电机的定子电阻为0.214 7 Ω,给定磁链为0.7 Wb,磁链容差为0.001 Wb,转矩容差为0.1 N·m。在两种情况下进行了对比。首先,给定空载转速的情况下,设电机的初始转速为400 r/min、0.3 s时转速为200 r/min、0.6 s时转速为800 r/min;其次,给定初始负载转矩为20 N·m、0.3 s时负载转矩为40 N·m、0.6 s时负载转矩为20 N·m,转速恒定为400 r/min,对系统性能进行分析,仿真结果如下。

当电机空载且恒定转速时,与传统DTC方法相比,本文新DTC方法中的磁链更光滑,脉动更小,尤其在高转速时更加明显,如图5所示。

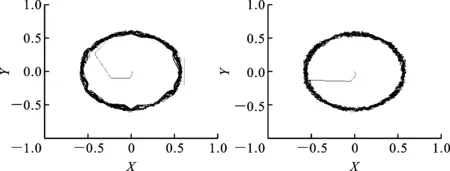
(a)传统DTC控制(转速为140 r/min) (b)新DTC控制(转速为140 r/min)

(c)传统DTC控制(转速为1 400 r/min) (d)新DTC控制(转速为1 400 r/min)图5 2种控制方法在电机空载且恒定转速时的定子磁链的空间分布图

当给定转速时,电机空载启动和转速突变两种情况下,本文新DTC方法的响应速度分别提高到约63%和96%。如图6所示。

(a)传统DTC控制(电机启动时) (b)新DTC控制(电机启动时)

(c)传统DTC控制(电机转速由400降到200 r/min) (d)新DTC控制(电机转速由400降到200 r/min)图6 2种控制方法在电机空载和转速突变时的转速波形图

给定转速、电机空载启动时,新DTC方法的电机转矩响应时间缩短了约30%,如图7所示。

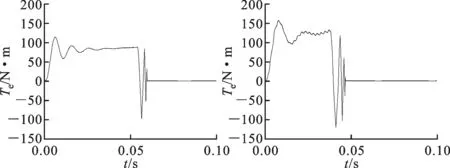
(a)传统DTC控制 (b)新DTC控制图7 2种控制方法在电机空载且给定转速时的启动转矩波形图

给定负载时,新DTC方法中,转矩纹波更小,且当转矩突变时,系统响应更快,如图8所示。

给定负载电机启动时,新DTC方法中的转速响应时间缩短了约28%,如图9所示。

5.2 实验结果分析

实际测试中,电机参数:PN=2 kW,n=1 450 r/min,TN=14 N·m,RS=2.33 Ω,LS=0.299 4 H,Rr=2.12 Ω,Lr=0.300 7 H,Lm=0.286 6 H,负载为200 N·m,通过38∶1的减速机连接到电机轴上,实测电机A相的电流波形图如图10所示。

(a)传统DTC控制 (b)新DTC控制

(c)传统DTC(转矩由20升到40 N·m) (d)新DTC(转矩由20升到40 N·m)图8 2种控制方法给定负载时电机转矩波形图

(a)传统DTC控制 (b)新DTC控制图9 2种控制方法在给定负载电机启动时的转速波形图

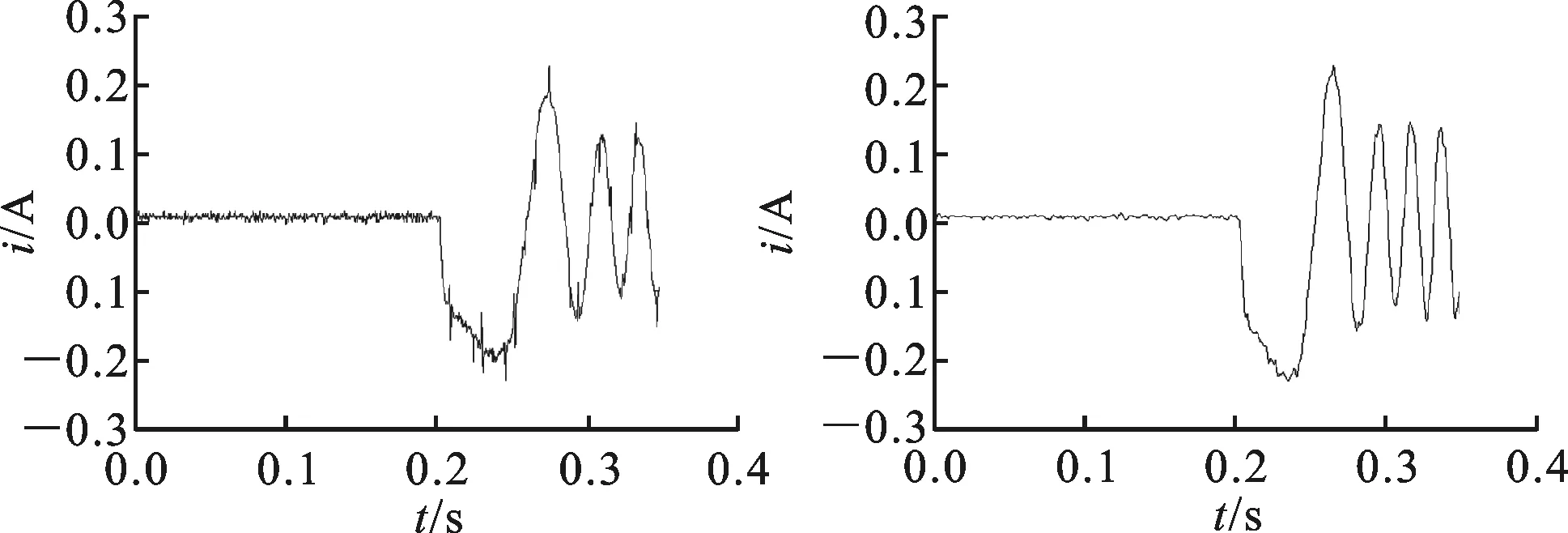
(a)传统DTC控制 (b)新DTC控制图10 2种控制方法在给定负载、转速恒定时电机的启动电流波形图

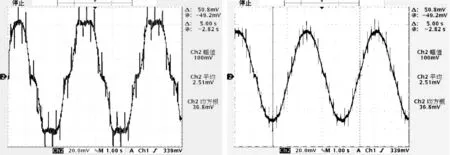
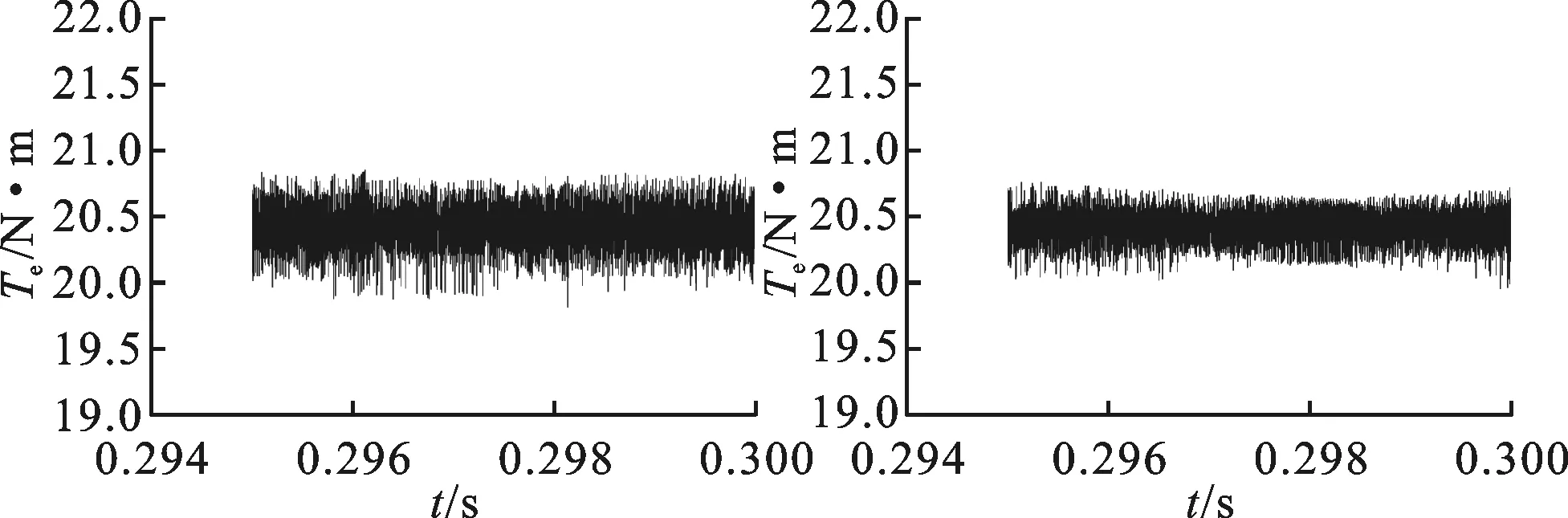
(a)传统DTC控制 (b)新DTC控制图11 2种控制方法在给定负载、转速恒定时电机稳定运行的电流波形截屏图

由图10及图11可知,给定负载时,新DTC方法中的电流响应速度更快,电流曲线更平滑,脉动更小。

仿真和实验结果表明,本文提出的异步电动机直接转矩控制方法的系统磁链波动更小,且可以很好地跟踪电机的给定转速和转矩,不仅响应快而且脉动小,电流更加平滑,无论在启动时刻,还是负载突变时刻都有更好的控制性能。

6 结束语

异步电动机的直接转矩控制方法对定子磁链的区间判断要求严格,选择的定子电压矢量决定着系统的磁链和转矩将增加或减小,进而决定了控制系统的性能好坏。本文通过分析定子电阻压降的影响以及磁链和转矩控制公式,提出转矩增加的前提条件和磁链变化的临界条件,重新确定电压矢量对磁链和转矩的作用范围,优化电压矢量选择表;在转矩脉动全局最小的条件下,得到改进的占空比计算方法。仿真和实验分析表明,基于以上两点提出的直接转矩控制方法具有更好的控制精度和跟随性能,达到了优化转矩的目的。

[1] 杨家强, 黄进. 基于转矩预测的异步电动机直接转矩控制研究 [J]. 浙江大学学报, 2005, 39(9): 1277-1281. YANG Jiaqiang, HUANG Jin. Research on direct torque control of induction machine based on torque prediction [J]. Journal of Zhejiang University, 2005, 39(9): 1277-1281.

[2] GAO H, DAS S, WU B. A space vector modulation based direct torque control scheme for a current source inverter fed induction motor drive [C]∥Proceedings of the 41st Annual Conference of the IEEE Industrial Electronics Society. Piscataway, NJ, USA: IEEE, 2015: 1307-1312.

[3] SUMAN K, SUNEETA K, SASIKALA M. Direct torque controlled induction motor drive with space vector modulation fed with three-level inverter [C]∥Proceedings of the IEEE International Conference on Power Electronics, Drives and Energy Systems. Piscataway, NJ, USA: IEEE, 2012: 1-6.

[4] KANG J K, SUL S K. New direct torque control of induction motor for minimum torque ripple and constant switching frequency [J]. IEEE Transactions on Industry Applications, 1999, 35(5): 1076-1082.

[5] ADAM A A, GULEZ K, ALISKAN I, et al. Steering DTC algorithm for IPMSM used in electrical vehicle (EV)-with fast response and minimum torque ripple [C]∥Proceedings of the 11th IEEE International Workshop on Advanced Motion Control. Piscataway, NJ, USA: IEEE, 2010: 279-283.

[6] ZHAO Shuai, YU Haisheng, YU Jinpeng, et al. Induction motor DTC based on adaptive SMC and fuzzy control [C]∥Proceedings of the 2015 27th Chinese Control and Decision Conference. Piscataway, NJ, USA: IEEE, 2015: 4474-4479.

[7] 吴晓东, 南余荣. 无速度传感器十二区段直接转矩控制 [J]. 机电工程, 2008, 25(3): 46-48. WU Xiaodong, NAN Yurong. Twelve section without speed sensor [J]. Mechanical and Electrical Engineering, 2008, 25(3): 46-48.

[8] ESSAADI M, KHAFALLAH M, SAAD A, et al. A comparative analysis between conventional and new direct torque control strategies of induction machine [C]∥Proceedings of the 2014 2nd World Conference on Complex Systems. Piscataway, NJ, USA: IEEE, 2014: 350-354.

[9] 廖晓钟, 邵立伟. 直接转矩控制的十二区段控制方法 [J]. 中国电机工程学报, 2006, 26(6): 167-173. LIAO Xiaozhong, SHAO Liwei. Twelve section control method for direct torque control [J]. Chinese Journal of Electrical Engineering, 2006, 26(6): 167-173.

[10]李夙. 异步电动机直接转矩控制 [M]. 北京: 机械工业出版社, 1994: 5-7.

[11]FLACH E, HOFFMANN R, MUTSCHLER P. Direct mean torque control of an induction motor [EB/OL]. (2008-11-19) [2015-04-11]. http:∥tubiblio.ulb.tu-darmatadt.de/12940.

[12]ZHANG Yongchang, ZHU Jianguo. Direct torque control of permanent magnet synchronous motor with reduced torque ripple and commutation frequency [J]. IEEE Transactions on Power Electronics, 2011, 26(1): 235-248.

[本刊相关文献链接]

王悍枭,刘凌,吴华伟.改进型滑模观测器的永磁同步电机无传感器控制策略.2016,50(6):104-109.[doi:10.7652/xjtuxb201606016]

常雪剑,彭博,刘凌,等.新型非奇异终端滑模观测器的永磁同步电机无传感器控制.2016,50(1):85-91.[doi:10.7652/xjtuxb201601014]

李彪,李黎川.新型磁链观测算法及其在永磁同步电机无位置传感器控制中的应用.2015,49(11):102-109.[doi:10.7652/xjtuxb201511017]

常雪剑,刘凌,崔荣鑫.永磁同步电机非奇异快速终端可变边界层滑模控制.2015,49(6):53-59.[doi:10.7652/xjtuxb 201506009]

郭伟,王跃,李宁.永磁同步电机飞轮储能系统充放电控制策略.2014,48(10):60-65.[doi:10.7652/xjtuxb201410010]

(编辑 刘杨)

A Direct Torque Control Method for Inductive Motor with Torque Optimization

LIU Xiaoyong,ZHENG Aihong,JIANG Feng,ZAN Xin,CAO Jianfu

(School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

A direct torque control method for optimizing the torque performance of inductive motors is proposed to address the issues that the flux control is asymmetric and the torque ripple is large in the traditional direct torque control. First, the voltage vector selection table is improved by redividing the range of the effects caused by voltage vectors on the stator flux and electromagnetic torque, and the required voltage vector is selected to reduce the torque ripple when the torque and the flux linkage change. The method considers the necessary condition that the torque increases and the critical condition that the flux changes when the voltage vector is selected. Moreover, the optimal torque error is derived from the torque ripple formula, and the duty cycle calculation is presented under the condition of the global minimum torque ripple. Then the control formula of stator flux and electromagnetic torque is given. Experimental results and a comparison with the traditional direct torque control method show that the dynamic response of the system is improved by 30%, the torque and the current ripple are reduced, and the flux linkage control is more close to the circular trajectory. It is concluded that the proposed method is applicable to engineering.

inductive motor; direct torque control; torque ripple; voltage vector; duty ratio

2016-04-11。 作者简介:刘小勇(1972—),男,副教授。 基金项目:国家自然科学基金资助项目(61573272)。

时间:2016-10-10

10.7652/xjtuxb201612003

TM921.51

A

0253-987X(2016)12-0012-07

网络出版地址:http: ∥www.cnki.net/kcms/detail/61.1069.T.20161010.1753.006.html