免疫粒子群优化RBF神经网络的变压器故障诊断

李 浩 王福忠 王 锐

(河南理工大学电气工程与自动化学院，河南 焦作 454000)



免疫粒子群优化RBF神经网络的变压器故障诊断

李 浩 王福忠 王 锐

(河南理工大学电气工程与自动化学院，河南 焦作 454000)

电力变压器运行的可靠性直接关系到电力系统的安全性及供电的可靠性。为提高变压器内部绝缘故障诊断的准确率，通过分析变压器油中溶解气体组分含量和变压器内部绝缘故障，提出了一种免疫粒子群优化RBF神经网络的变压器故障诊断算法。介绍了基于人工免疫网络算法确定RBF网络隐层中心数目和初始位置的方法，以及基于粒子群算法优化RBF网络权重的方法。仿真结果表明，该算法能有效诊断变压器故障类型，提高故障诊断的准确率。

变压器 故障诊断 RBF神经网络 人工免疫网络算法 粒子群算法 最小二乘法 可靠性

0 引言

电力变压器是电力系统的重要设备，正确诊断电力变压器绝缘故障对提高电力系统运行安全性和可靠性具有重要意义[1]。变压器油中溶解气体组分分析(dissolved gas analysis,DGA)技术是目前诊断油侵式变压器内部绝缘故障最有效的方法之一。它能够有效发现变压器内部潜伏性故障及其发展程度，从而防止由此引发的安全事故[2]。为提高变压器绝缘故障诊断准确率，目前在变压器油中溶解气体分析的基础上，引入许多智能算法，如人工神经网络[3-5]、人工免疫算法[6]、支持向量机[7]、粒子群算法等。

神经网络算法具有自组织、自学习、无需建立具体物理模型等优点，在模式识别、故障诊断等领域获得了广泛应用，但该算法也存在训练样本需求量大、训练时间长以及容易陷入局部最小等缺陷。为提高变压器绝缘故障诊断准确率，本文提出采用免疫粒子群优化径向基函数(radial basis function,RBF)神经网络算法，并将其应用于变压器故障诊断。

1 RBF神经网络

RBF是一种前馈型神经网络，在数值计算、模式识别、函数拟合、故障诊断等领域获得了广泛的应用。RBF神经网络由输入层、隐含层和输出层3部分组成，其网络结构如图1所示。

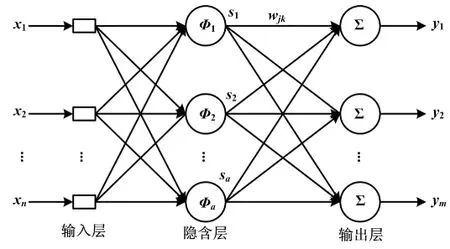
图1 RBF网络结构图

RBF神经网络的主要原理是：网络隐层单元的非线性作用过程采用RBF激励函数作为隐层单元的“基”构成隐含层空间，代表从n维输入空间到m维输出空间的非线性映射f：Rn→Rm。径向基函数的基本形式如式(1)所示。

Sj(x)=φj(‖x-cj‖) j=1,2,…,a

(1)

在RBF神经网络中,高斯函数由于具有表达形式简单、解析性好、光滑性好以及任意阶次可微分等优点而成为常用的径向基函数。因此，本文采用高斯函数作为径向基函数，其基本形式如式(2)所示。

φj(‖x-cj‖)

(2)

式中:φj()为基函数；‖x-cj‖为输入向量x与基函数中心向量cj之间的欧式距离；cj为隐含层基函数的中心向量；δj为隐含层第j个基函数的宽度参数。

网络的隐含层到输出层为线性映射，网络的输出层为隐含层节点的线性组合，其表达式如式(3)所示。

(3)

2 基于RBF神经网络的变压器故障诊断模型

2.1 故障诊断模型输入/输出设计

在变压器油井的DGA过程中，根据油中溶解气体类型与内部绝缘故障性质的对应关系，以及油中溶解的氢气(H2)、甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)、乙炔(C2H2)、一氧化碳(CO)和二氧化碳(CO2)7种特征气体的含量判断变压器绝缘故障。由于CO、CO2含量分散且现场获得的数据常有缺失，因此本文选取H2、CH4、C2H6、C2H4、C2H2这5种气体作为特征气体，并将这5种特征气体的含量作为神经网络的输入量。

变压器内部绝缘故障主要有放电性故障和过热性故障。根据《变压器油中溶解气体分析和判断导则》，本文选取局部放电(PD)、低能放电(D1)、高能放电(D2)、低温过热(T1)、中温过热(T2)、高温过热(T3)6种模式作为网络的输出向量。设定网络的实际输出以0～1之间的数值表示对应故障发生的程度，数值越接近1，表示发生此类故障的可能性越大。

设网络的输入数据共有N组，X=[x1,x2,…,xN]，每个元素xi=[xi1,xi2,xi3,xi4,xi5]T代表一组故障数据，与其对应的神经网络实际输出为Y=[yi1,yi2,yi3,yi4,yi5,yi6]。由于RBF神经网络的隐含层到输出层为线性映射，所以根据图1所示的网络结构，可得到网络的输出层结果表达式如下。

Φ

(4)

式中:yk为输出层节点k的输出；wk=[wk1,wk2,…,wka]为输出层节点k的权值矢量；Φ=[φ1,φ2,…,φa]T为基函数矢量。

由式(4)可知，构建RBF神经网络故障诊断模型的关键在于以下两个方面。

①利用输入故障样本，确定隐含层中心向量以及隐含层神经元个数。

②根据给定的训练样本，训练网络隐含层到输出层权值。常用的求解RBF网络中心算法主要有聚类算法、正交最小二乘算法等。但是这些算法都存在自身的缺陷，例如聚类算法需要预先指定聚类的数量，而正交最小二乘法在输入数据量较大时会出现病态矩阵[8]问题。为克服这类问题，本文采用人工免疫网络算法，对输入网络的训练数据集进行处理，进而得到RBF网络的隐层中心数目及位置。

2.2 基于人工免疫网络算法的RBF隐层中心的确定

人工免疫网络算法是一种模拟生物免疫系统的新型智能算法。该算法将克隆选择和免疫抑制原理有机结合，通过模拟抗原与抗体之间的作用关系，使抗体在学习抗原模式的过程中不断优化，从而得到能够表征抗原特征的独特性抗体[9]。本文采用人工免疫网络原理，对输入RBF网络的变压器故障样本数据进行处理，从而求得网络隐层中心数与中心矢量。

变压器故障样本数据处理算法如下。

①原始抗原集提取。由上文可知，本文选取H2、CH4、C2H6、C2H4、C2H2这5种气体作为变压器发生故障时的特征气体，选取这5种特征气体的含量作为原始抗原集，设为xi=[xi1,xi2,xi3,xi4,xi5]。

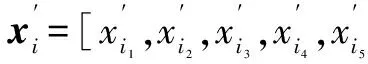
(5)

③随机初始化抗体集合。随机抽取一定数目(N)的各类故障模式的训练样本，生成免疫网络的初始抗体集合Ab。

(6)

⑤克隆选择。根据亲和度向量fi，从抗体集合Ab中选择n个亲和度最高的抗体构成新的抗体集合Ab{n}。

⑥克隆操作。对新的抗体集合Ab{n}中的每个抗体进行克隆操作，克隆数目Nc由式(7)决定，经过克隆操作后的抗体集为Ci。

(7)

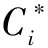
(8)

⑨免疫抑制操作。计算抗体集Ab*中各个抗体之间的亲和度，删除亲和度大于特定阈值σs的抗体，更新抗体集Ab*。

⑩重复上述操作,直到达到规定的迭代次数为止。

2.3 RBF网络权值的粒子群优化算法

粒子群算法(particleswarmoptimization,PSO)是一种基于群体智能的优化算法。同其他优化算法，如遗传算法(geneticalgorithm,GA)等相比，粒子群算法具有简单、易实现以及更强的局部与全局寻优能力等优点，因此本文选用粒子群算法优化RBF网络模型的连接权值。

在PSO中，采用位置与速度模型进行搜索，每个粒子代表解空间中的一个潜在解。假设m个粒子组成的一个群体在R维(每个粒子的维数)解空间中以一定的速度飞行；每个粒子由自身的位置和速度向量表示，记为Pi=(Pi1,Pi2,…,PiR)、Vi=(Vi1,Vi2,…,ViR)；每个粒子个体搜索到的最优值记为BestPi；群体搜索到的最优值记为BestGi，则每个粒子的速度和位置可根据式(9)和式(10)计算得到。

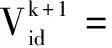
(9)

(10)

式中：i=1,2,…,m；d=1,2,…,R;ω为惯性因子；C1、C2为学习因子；R1、R2为[0,1]之间的随机数；k为迭代次数。

采用粒子群算法寻找RBF神经网络的最佳权重，设定群体中每个粒子的位置向量为RBF神经网络的一组权值，随机产生多个粒子，也即产生了多组网络权值组成粒子群。采用PSO搜索最优位置，当目标函数值达到最小时，即可得到网络中的最佳连接权重。其优化算法如下。

①初始化粒子群。确定粒子个数m，设定学习因子C1、C2，设定最大迭代次数kmax，随机产生粒子的位置向量Pi和速度向量Vi。

②计算每个粒子的适应值。根据RBF神经网络的输出，计算每个粒子的适应度值，记录每个个体粒子的极值以及群体粒子的极值，分别用BestP和BestG来表示。

整个网络的适应值评价函数如式(11)所示:

(11)

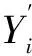
③比较粒子的适应值和个体极值BestP处的适应值，取最优者作为该粒子新的个体极值BestP；比较粒子的适应值和全局极值BestG处的适应值，取最优者作为种群新的全局极值BestG。

④根据式(9)、式(10)，对粒子的位置向量和速度向量进行更新。

⑤如果达到最大迭代次数kmax或满足网络的精度要求，就停止迭代输出结果，否则返回第②步。

3 仿真分析

3.1 仿真样本的选取

为提高网络训练的准确性，本文以某变压器油中溶解气体含量值为例，收集已知故障类型的样本数据300组。随机选择其中的120组包含各个故障类型的气体特征量集作为训练集，剩下的180组作为测试上述算法性能的测试集。

3.2 仿真过程

将经过人工免疫网络算法处理所得的结果作为RBF神经网络隐含层中心数量和位置。采用粒子群算法对网络进行权值寻优，粒子群参数设置如下：群体大小m=40；学习因子C1=C2=2；最大惯性因子ωmax=1.4；最小惯性因子ωmin=0.4；最大迭代次数kmax=100。输入RBF网络的数据是5种特征气体的体积分数向量及其对应故障类型编码向量的集合。为训练神经网络的权重，需对变压器的故障类型进行编码，以作为RBF神经网络的期望输出，具体如表1所示。

表1 故障类型期望输出编码

3.3 诊断结果

将剩余180组气体特征量用于测试训练后的RBF神经网络的诊断精度，诊断结果如表2所示。

表2 诊断结果

表3列出了5组典型变压器故障实例与采用该算法诊断出的结果。

为验证本文方法在诊断变压器故障类型上具有较高的准确性，此处将收集到的故障数据依次采用IEC三比值法、BP神经网络算法和标准RBF神经网络算法进行诊断，结果如表4所示。

表3 5组变压器故障诊断实例

表4 不同诊断算法诊断精度对比

由表2可以看出，不同的变压器故障类型有不同的诊断准确率，T2的诊断准确率相对较低，但也达到了89.5%；T1、D1和D2的诊断准确率居中，平均约为91%左右；T3和PD的诊断准确率最高，平均达到93%以上。由表3所示的诊断结果可以看出，本文采用的变压器故障诊断算法，对5组故障实例均可正确诊断。比较表2和表4可以看出，较其他几类算法，本文采用的算法具有较高故障诊断率。

4 结束语

本文将变压器油中溶解气体含量作为研究对象，针对电力变压器内部绝缘故障，采用RBF神经网络算法作为变压器故障诊断模型基础，对变压器的故障进行诊断。为提高变压器绝缘故障诊断的精度，在RBF神经网络原理的基础上，引入了人工免疫网络算法与粒子群优化算法。采用人工免疫网络算法对故障数据进行处理，能够较好地求得RBF隐含层节点数目及中心向量，精简RBF神经网络结构，提高网络的泛化能力。采用粒子群算法训练网络权值，提高了网络的全局收敛能力。

从仿真结果可以看出，将人工免疫网络算法与粒子群优化算法结合并用于优化RBF神经网络的方法，对诊断变压器故障类型非常有效。该方法能够有效提高变压器故障诊断的精度。

[1] 郑蕊蕊,赵继印,赵婷婷,等.基于遗传支持向量机和灰色人工免疫算法的电力变压器故障诊断[J].中国电机工程学报,2011,31(7):57-63.

[2] 吴晓辉,刘炯,梁永春,等.支持向量机在电力变压器故障诊断中的应用[J].西安交通大学学报,2007,41(6):722-726.

[3] 项文强,张华,王姮,等.基于L-M算法的BP网络在变压器故障诊断中的应用[J].电力系统保护与控制,2011,39(8):100-103.

[4] 王雪梅,李文申,严璋.BP网络在电力变压器故障诊断中的应用[J].高电压技术,2005,31(7):12-14.

[5] 陈江波,文习山,蓝磊,等.基于新径向基函数网络的变压器故障诊断法[J].高电压技术,2007,33(3):140-143.

[6] 周爱华,张彼德,张厚宣.基于人工免疫分类算法的电力变压器

故障诊断[J].高电压技术,207,33(8):77-80.

[7] 董明,孟源源,徐长响,等.基于支持向量机及油中溶解气体分析的大象电力变压器故障诊断模型研究[J].中国电机工程学报,2003,23(7):88-92.

[8] 任静,黄家栋.基于免疫RBF神经网络的变压器故障诊断[J].电力系统保护与控制,2010,38(11):6-9.

[9] 熊浩,孙才新,陈伟根,等.电力变压器故障诊断的人工免疫网络分类算法[J].电力系统自动化,2006,30(6):57-60.

[10]赵安新,汤晓君,王尔珍,等.变压器油溶解气体的FTIR定量分析[J].光谱学与光谱分析,2013,33(9):2407-2410.

[11]王华国,孙玉坤,王博,等.改进的PSO-FNN在发酵软测量中的应用[J].自动化仪表,2016,37(3):62-64.

[12]王晓霞,王涛.基于粒子群优化神经网络的变压器故障诊断[J].高电压技术,2008,34(11):2362-2367.

Transformer Fault Diagnosis by Using RBF Neural Network Optimized by Immune Particle Swarm

The operational reliability of the power transformer is closely linked to the security of power system and the reliability of power supply.In order to improve the accuracy of fault diagnosis for internal insulation of transformer,by analyzing the contents of the dissolved gas components in transformer oil,and the fault of internal insulation,the fault diagnosis algorithm using RBF neural network optimized by immune swarm optimization algorithm is put forward.The method based on artificial immune network algorithm for determining the number and the initial position of hidden layer centers in RBF network center; as well as the method based on particle swarm optimization for optimizing the weights of RBF network are introduced.The results of simulation show that the proposed algorithm can effectively diagnose the fault types of transformer and improve the accuracy of fault diagnosis.

Transformer Fault diagnosis RBF neural network Artificial immune network algorithm Particle swarm optimization algorithm Least square method Responsibility

国家自然科学基金资助项目(编号：61104079);

河南省产学研基金资助项目(编号：132107000027)。

李浩(1992—)，男，现为河南理工大学电气工程专业在读硕士研究生；主要从事电气设备故障诊断方向的研究。

TH18;TP183

A

10.16086/j.cnki.issn 1000-0380.201611002

修改稿收到日期：2016-04-14。