钢框架−装配式混凝土抗侧力墙板结构基于性能的抗震设计方法
吴函恒,周天华,陈军武, 2,吕晶
钢框架−装配式混凝土抗侧力墙板结构基于性能的抗震设计方法
吴函恒1,周天华1,陈军武1, 2,吕晶1
(1. 长安大学建筑工程学院,陕西西安,710061;2. 陕西有色建筑设计研究院有限公司,陕西西安,710054)
为研究钢框架−预制混凝土抗侧力墙板装配式结构体系(SPW体系)的基于性能的抗震设计方法,对4榀钢框架−预制混凝土抗侧力墙板结构足尺试件进行低周反复荷载作用下的试验研究。对SPW体系的抗震性能水平及性能指标的量化进行研究,提出5个性能水平的失效判别标准,并给出不同性能水平对应的层间位移角限值建议;提出SPW结构体系直接基于位移的抗震性能设计方法和设计步骤,并通过算例给出16层SPW结构体系的基于性能的抗震设计过程。实验结果表明:该结构体系为一种典型的双重抗侧力体系,加载过程呈现出明显的2个阶段性,抗侧力墙板为结构体系的第1道防线,钢框架为结构的第2道防线。
钢框架;混凝土抗侧力墙板;装配式结构;抗震性能指标;设计方法
钢框架与内填式混凝土墙组成的双重抗侧力体系能充分结合二者的优点,具有抗侧刚度大、延性好、多道抗震设防的特点[1−4]。钢框架—预制混凝土抗侧力墙装配式结构体系(简称“SPW体系”)[5]是在推动建筑产业化和现代化的背景下,提出的一种新型装配式双重抗侧力结构体系,其主要抗侧力组成−钢框架和预制装配式混凝土抗侧力墙板均可实现预制装配化,具有施工周期短,现场湿作业少、节省人力、效率提高等优点。周天华等[6−7]对4榀由钢框架和型钢混凝土抗侧力墙、钢筋混凝土抗侧力墙组成的单层单跨足尺SPW体系结构模型开展水平低周反复加载试验研究,研究表明:该体系能充分结合钢框架与混凝土抗侧力墙板的优点,具有抗侧刚度大、延性好、多道抗震设防的优点,在抗震设防区具有广泛的应用前景。周天华等[8]对SPW体系的竖向受力性能进行研究,表明:预制墙体顶部连接板的长圆孔构造形式能有效地降低墙体的轴压比,使墙体仅承担使用阶段活荷载所传递而来的竖向力。本文作者在试验研究的基础上,总结了SPW体系的抗震性能和破坏机理,并结合我国抗震设计规范[9]基于性能的抗震设计目标,将该结构体系的抗震性能划分为5个水平,并根据试验结果,给出5个性能水平对应的层间位移控制指标限值,建立SPW装配式结构体系的抗震性能目标,提出基于性能的抗震设计方法,为后续理论研究和工程应用提供参考。
1 试验概况及破坏形态
1.1 试验概况
对4榀足尺单层单跨SPW结构进行了水平低周反复加载试验,其中试件SPW-1,SPW-2的墙体为型钢混凝土抗侧力墙板,试件SPW-a和b的墙体为钢筋混凝土抗侧力墙板,框架柱、梁规格为分别为HW300×300×10×15和HN350×175×7×11,钢材材质为Q235B级,梁柱节点采用栓焊式刚性连接,并按照文献[9]进行了“强节点”设计,预制混凝土抗侧力墙高2 430 mm,宽1 200 mm,厚度为120 mm,混凝土设计强度等级为C30级,水平分布钢筋为8@100(双层),竖向分布钢筋采用6.5@100(双层),暗柱尺寸为250 mm×120 mm,内配66.5纵向钢筋,箍筋6.5@100/200(加密区/非加密区),加密区高度为暗柱上下各500 mm范围,试件SPW-1和SPW-2在暗柱内均设置I10型钢。试件几何尺寸和连接构造如图1所示。
按照采用力和位移控制加载模式[10],对顶部框架梁施加水平低周反复荷载,直至试件发生破坏。水平加载过程中,框架柱顶部保持500 kN的竖向荷载。
1.2 试件破坏形态
图2所示为试件SPW-1和SPW-2的破坏过程。钢框架−型钢混凝土墙体试件(SPW-1,SPW-2)。抗侧力墙板作为第1道防线,在加载前期承担主要的水平荷载,随着荷载的增大,抗侧力墙板呈现出弯曲型破坏的特点,角部受压区混凝土压碎、剥落进而出现露筋现象,损伤累积严重(图2(a)),角部受拉区型钢端部达到屈服状态,此时水平荷载达到峰值max,而通过应变观察,钢框架仍处在弹性阶段;墙体逐步退出工作后,荷载向钢框架转移,框架梁、柱端先后出现较大塑性变形(图2(b),2(c)),而抗侧力墙板在加载后期由于变形过大,在型钢和混凝土界面发生“黏结滑移”破坏(图2(d))。
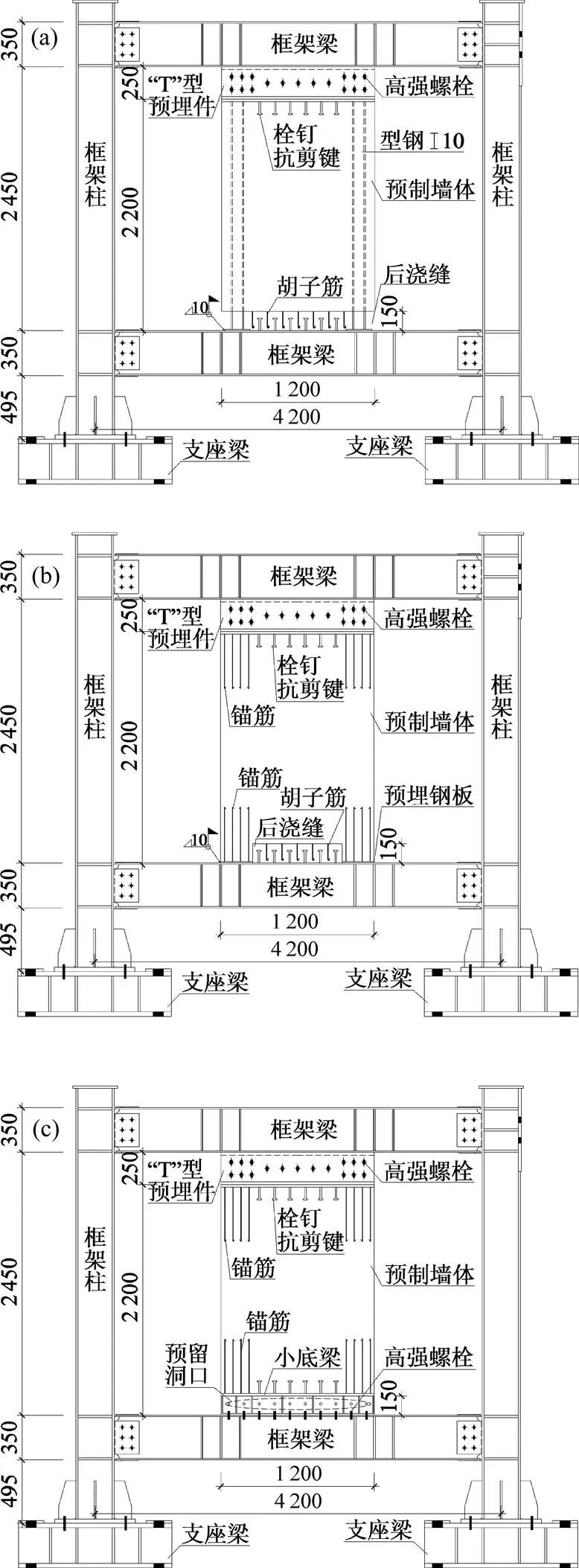
单位:mm

(a) 角部混凝土压碎、露筋;(b) 框架梁端塑性变形;(c) 框架柱端塑性变形;(d) 型钢与混凝土界面处竖向裂缝
图3所示为试件SPW-a和SPW-b的破坏过程。钢框架−钢筋混凝土墙体试件(SPW-a,SPW-b)。在加载前期,抗侧力墙板承担主要的水平荷载,随着荷载的增大,抗侧力墙板顶部预埋锚筋和栓钉抗剪键发生破坏(图3(a)),墙体顶部连接失效(图3(b)),抗侧力墙板完全退出工作;继续加载,结构由双重抗侧力体系变为单一的钢框架体系,并相继在梁端和柱端出现塑性铰(图3(c),3(d)),钢框架达到承载能力的极限状态。
由图3可以看出:结构体系的破坏过程呈现出较为明显的2个阶段:第1阶段,抗侧力墙板承担大部分水平荷载,达到其承载能力的极限状态,试件SPW-1,SPW-2的抗侧力墙板发生弯曲型破坏、试件SPW-a,SPW-b的抗侧力墙板发生连接型破坏;第2阶段,钢框架承担主要水平荷载,达到其承载能力的极限状态。结构体系在不同受力阶段的破坏特征,如表1所示。

(a) 角部锚筋连接失效;(b) 墙体顶部连接失效;(c) 框架梁端塑性变形;(d) 框架柱端塑性变形

表1 试件各受力阶段的破坏形态
2 结构体系的性能指标
钢框架−混凝土抗侧力墙装配式结构体系(SPW体系)属于一种典型的双重抗侧力体系,其破坏过程具有明显的2阶段性,抗侧力墙板与钢框架在整个破坏过程中先后发挥抗侧力功能,根据试验研究结果,将SPW体系的抗震性能划分为正常使用、暂时使用、修复后使用、生命安全和防止倒塌5个水平,表2给出各个性能水平的界定与宏观描述。
结构的破坏与倒塌主要取决于结构构件变形能力,《建筑抗震设计规范》(GB50011—2010)[9]以层间位移角作为结构的性能指标,层间位移角与结构的破坏程度有较好的相关性,能够反映结构层间各构件变形的综合结果和层高的影响,因此,本文以层间位移角作为SPW体系的性能指标。基于试验研究结果,表3给出SPW体系在5个性能水平下的层间位移角。
由表3可知:SPW体系对应于正常使用的性能要求时,层间位移角介于1/400~1/350之间;对应于暂时使用的性能要求时,层间位移角介于1/250~1/200之间;对应于修复后使用的性能要求时,层间位移角介于1/160~1/130之间;对应于生命安全的性能要求时,层间位移角介于1/65~1/50之间;对应于防止倒塌的性能要求时,层间位移角介于1/45~1/28之间。
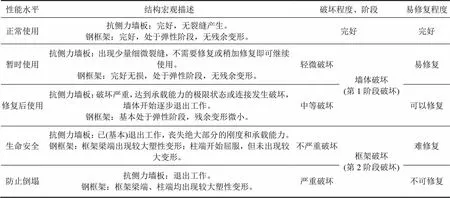
表2 SPW体系抗震性能水平及其宏观描述
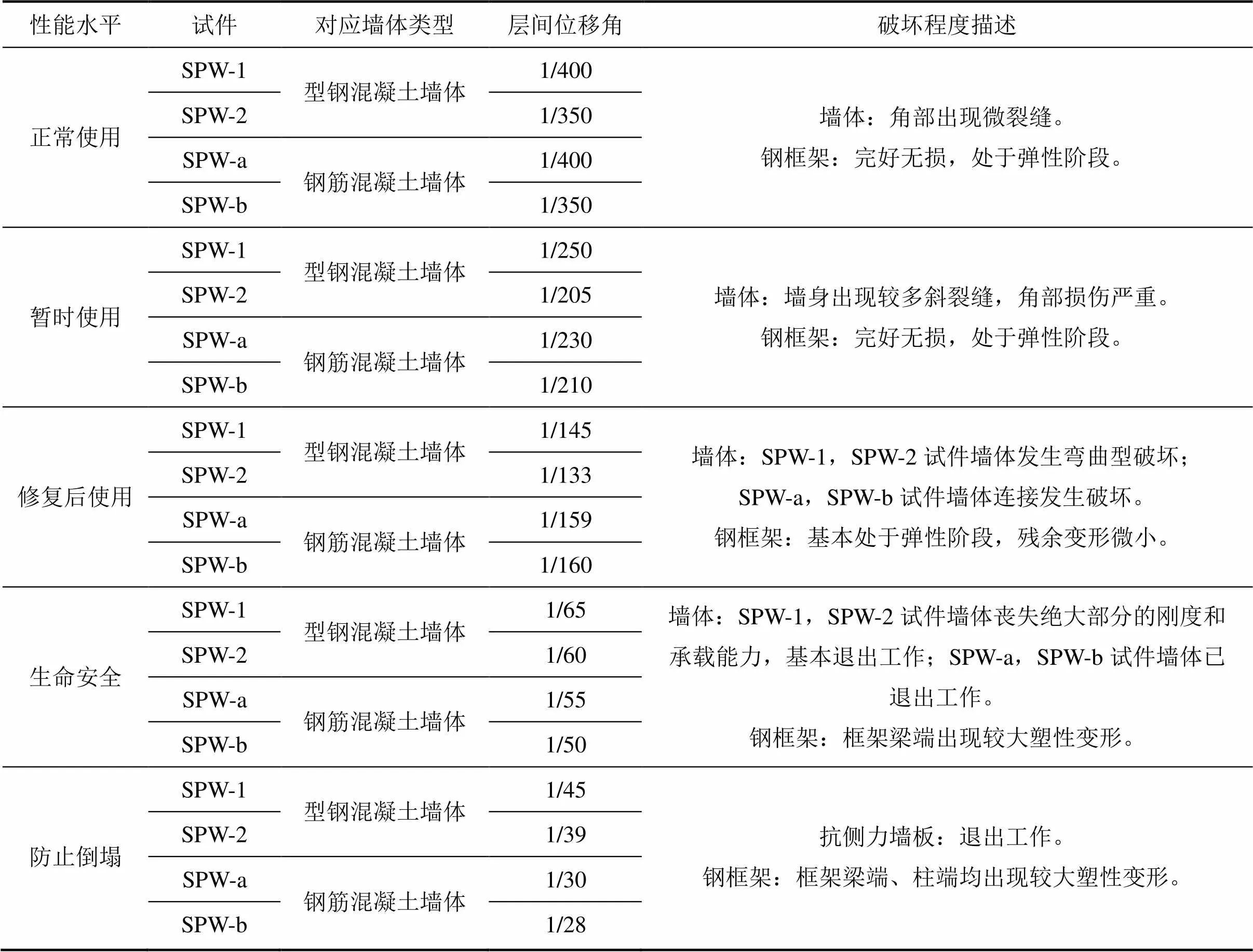
表3 SPW体系性能指标量化值
SPW体系是由钢框架与混凝土墙体组成的双重抗侧力体系,其变形性能应介于钢框架结构与混凝土剪力墙结构之间,综合文献[9, 11]对2种结构基于不同性能水平的层间位移角容许值的建议,并结合本次试验结果,本文偏保守的建议SPW装配式结构5个性能水平对应的层间位移角限值,见表4。

表4 层间位移角限值
3 基于性能的抗震设计方法
采用直接基于位移的抗震性能设计方法,在设计的开始阶段就按照结构的位移进行设计,可方便地控制结构在地震作用下的行为。基于位移的抗震设计需先确定结构的振动侧移模式,并将多自由度体系等效为单自由度体系,然后由等效的单自由度体系确定其弹塑性地震位移反应,并根据侧移模式反算出原多自由度体系各楼层的弹塑性地震位移反应。
3.1 侧移模式及目标侧移曲线
图4所示为结构的侧移模式。将结构的水平地震作用简化为倒三角分布,SPW结构体系在水平力为倒三角形分布模式下(见图4),任意截面高度处侧移()
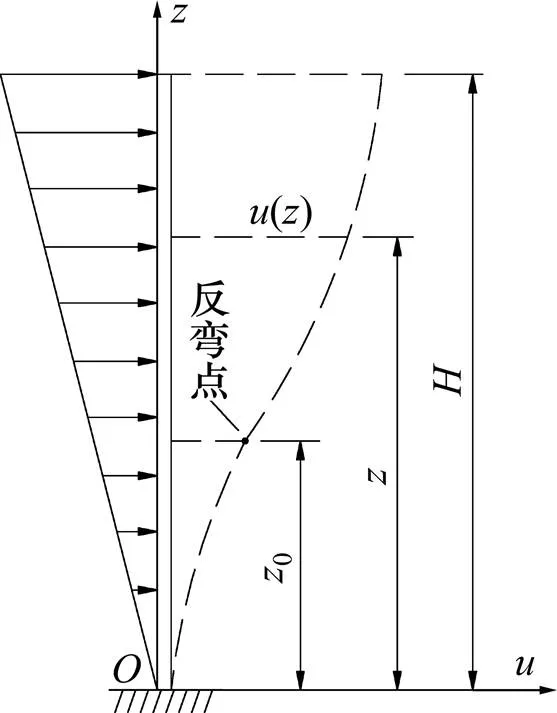
图4 结构的侧移模式
可表示为[12]
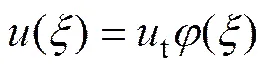
(2)
式中:,为结构任意截面的相对高度;t为结构的顶点位移;()为结构的侧移形状函数;为结构的总高度;为结构的刚度参数[12];为倒三角形分布的地震作用峰值。
SPW体系为钢框架与混凝土抗侧力墙板组成的双重抗侧力体系,其侧移曲线为弯剪型(见图4),侧移曲线上的反弯点相对高度0可由对式(1)求二阶导数为0得到,即:
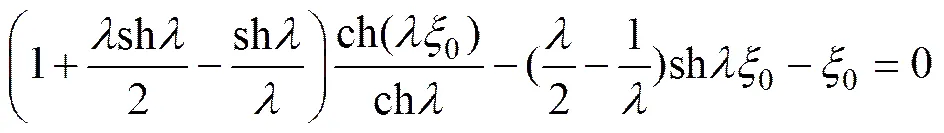
对平面和立面布置规则、且结构刚度和质量分布比较均匀的SPW结构体系,其反弯点所在楼层的层间侧移最先达到层间位移限值。设处的楼层为第层,令第层的层间位移达到某种性能水平的极限状态,则有
(4)
式中:为第层层高[]为某种性能水平对应的层间位移角限值,见表4。
由式(4)得
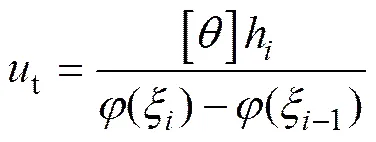
将式(5)代入式(1)可求出相应极限状态时的每层的侧移值(ξ)。
3.2 等效单自由度体系的等效参数
将多自由度体系等效为单自由度体系,如图5所示。其基本假定为:1) 多自由度体系与等效单自由度体系的基底剪力相等;2) 水平地震力在2种体系上所做的功相等。
根据上述假定,等效单自由度体系的等效质量eff、等效位移eff、等效刚度eff和基底剪力b分别为:
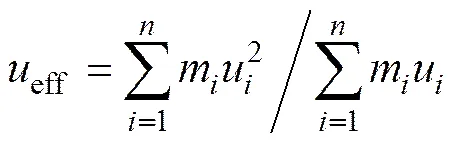
(7)
(a) 多自由度体系;(b) 位移形状;(c) 等效单自由度体系
图5 多自由度体系及等效单自由度体系
Fig. 5 Multi-degree and equivalent single-degree-of-freedom systems
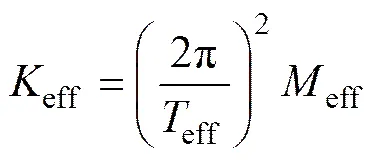
(9)
式中:i为各楼层的质量;u为各楼层处的侧移;eff等效单自由度体系的周期。
3.3 位移反应谱
基于位移的抗震性能设计是以位移反应谱为基础,根据我国现行抗震设计规范[9]的加速度反应谱a(),按下式换算为位移反应谱
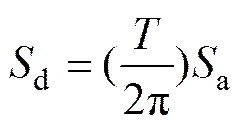
根据文献[9]的加速度反应谱,由式(10)可得
(11)
式中:max为水平地震影响系数最大值;1和2为地震影响系数曲线的调整系数,max,1和2的取值参见文献[9];当等效单自由度体系的等效位移eff已知(在式(11)中用d表示),由式(11)可确定相应的等效周期eff。
3.4 设计步骤
1) 根据功能要求进行初步结构设计,包括柱网布置、层高、构件截面尺寸等。
2) 根据业主要求和房屋的重要性程度,确定在一定强度水准地震作用下的性能目标及相应的层间位移角限值(见表4)。
3) 确定结构的初始目标侧移曲线。根据初步设计,计算侧移曲线上的反弯点相对高度0,设0处的楼层为第层,拟定第层的层间位移达到限值,按照式(2)和(5)计算(ξ),(ξ−1)和t;再按照式(1)计算各楼层处的侧移u。
4) 根据各楼层处的u和m,按式(6)和(7)分别确定等效单自由度体系的等效位移eff和等效质量eff。
5) 根据地震设防水准、等效阻尼比eff和等效位移eff由式(11)确定等效周期eff。其中等效阻尼比eff按下式确定[13]:
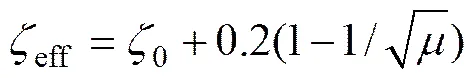
式中:0为结构在弹性阶段的黏滞阻尼比,SPW体系为钢框架与混凝土抗侧力墙板组成的双重抗侧力体系,参照取0.04,为位移延性需求,正常使用、暂时使用、修复后使用、生命安全和防止倒塌时对应的可分别取1.5,2.0,3.0,4.0和4.5。
6) 根据等效质量eff和等效周期eff,按式(8)确定等效单自由度体系的等效刚度eff,再将eff和eff代入式(9)求得基底剪力b,基底剪力b按倒三角形进行分配,确定各质点的水平地震作用。
7) 将水平地震作用和重力荷载进行组合,得到构件截面的内力设计值,进行构件承载力计算,并采取必要的构造措施。
8) 按上述步骤设计对SPW结构进行静力推覆分析,校核所得侧移形状,评价结构的变形能力和强度需求。如果由静力推覆分析得到的侧移形状不满足预期目标位移,则将分析结果中得到的结构某一层或几层达到相应位移角限值的侧移形状作为修正后的侧移形状重新进行计算。
4 算例及分析
某16层钢框架−预制混凝土抗侧力墙板装配式结构体系,层高为3 m,结构总高度48 m。抗震设防烈度为8度(0.20 g),设计地震分组为第1组,场地类别为Ⅱ类(g=0.35 s),楼(屋)面恒载为4 kN/m2(含楼板),活荷载为2 kN/m2,平面布置如图5所示。初步确定框架柱截面采用箱型截面,截面高度和宽度均为350 mm,壁厚为20 mm,框架梁采用H型钢截面,截面规格为HN400×200×8×13。钢材材质为Q345B级,抗侧力墙板墙宽3 000 mm,厚200 mm,混凝土墙体等级为C30,算例仅研究结构的横向受力情况,经过计算,得到总框架刚度F=189 493 kN,约束梁刚度B=114 788 kN,抗侧力墙板等效抗弯刚度eq=40 358 116 kN·m2,刚度参数=4.17,各楼层结构自重G=2 383 kN(=1, 2, 3, …, 16)。本例先按“正常使用”性能水平对SPW结构体系进行设计,然后按“修复后使用”和“防止倒塌”2个性能水平对设计结果进行校核分析。
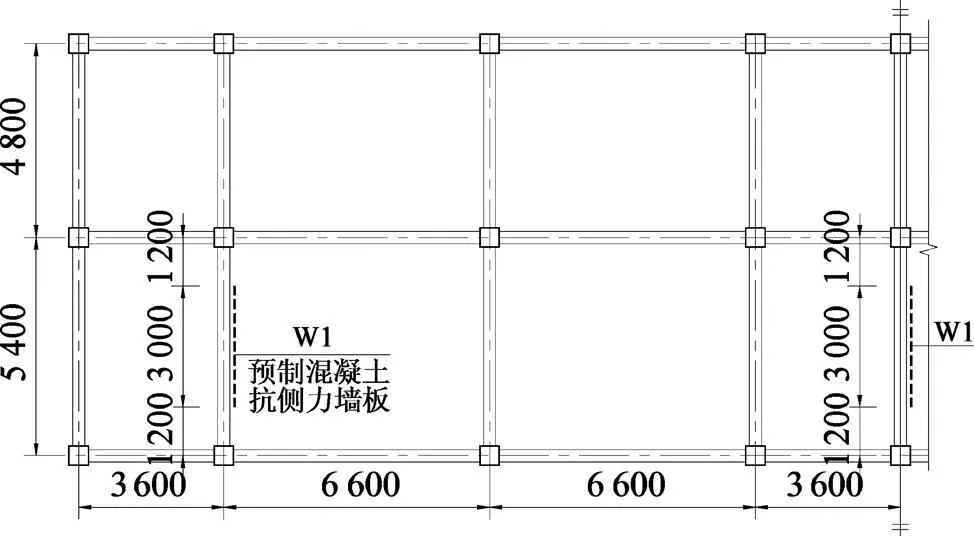
单位:mm
4.1 按“正常使用”性能水平设计
该结构的刚度参数=4.17,代入式(3)计算出反弯点相对高度0为0.48,则假定该结构第8层的层间位移达到“正常使用”层间位移角限值1/500,由式(1),(2),(5)得到各楼层的侧移u,如表1所示。各层位移u确定后,由式(6)和(7)确定等效单自由度体系的等效位移eff=53.1 mm和等效质量eff=2 746.5 t。
取延性系数=1.5,由式(12)确定等效阻尼比eff=0.077,将eff,eff,max=0.16和g=0.35代入式(11)确定等效周期eff=2.57s,由式(8)确定等效刚度eff=42.5 kN/mm,再由式(9)确定基底剪力b=2 250 kN。将基底剪力b按倒三角进行分配,即可确定各楼层的地震作用效应,并与相应的重力荷载及风荷载效应进行组合,得到各个构件的内力设计值。对于框架柱、框架梁进行截面验算,对抗侧力墙板进行截面配筋设计并采取相应构造措施。
利用Midas/GEN对所设计的结构进行静力推覆分析(pushover),分析模型如图7所示。结构基底剪力达到2 253.6 kN(第79加载步)时的侧移曲线与按“正常使用”性能水平设计时采用的侧移曲线(式(1))的对比见图8。由图8可知:在相同地震作用的情况下,结构的变形需求小于结构的变形能力,满足8度多遇地震下“正常使用”的性能水平要求。

图7 pushover分析模型
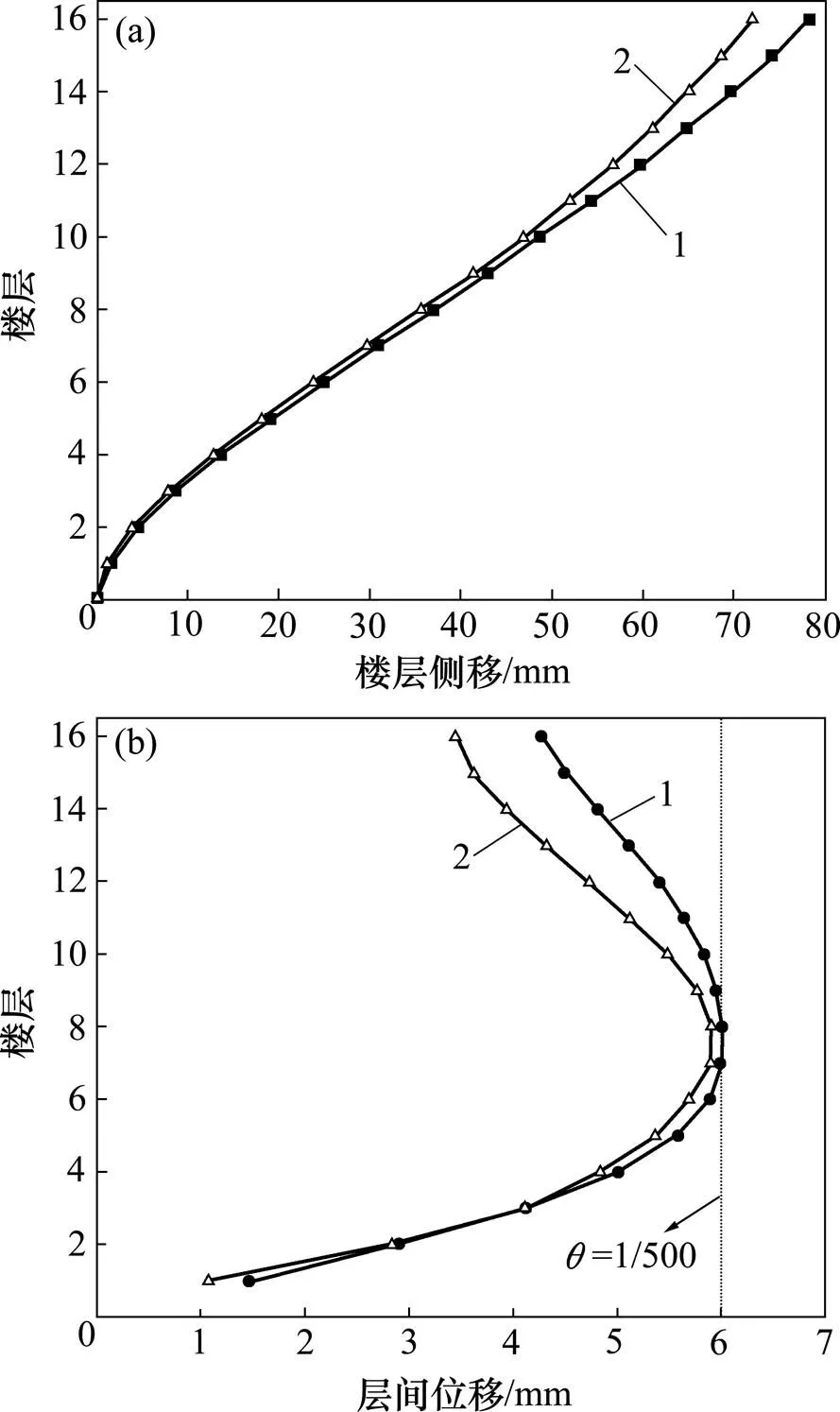
(a) 楼层侧移;(b) 层间位移
4.2 按“修复后使用”性能水平校核
按“修复后使用”性能水平校核,当推覆加载至第202步时,结构的第8层首先达到“修复后使用”状态的层间位移角限值(=1/200),取相应的推覆曲线作为楼层目标侧移曲线,代入式(6)和(7),计算得到等效单自由度体系的等效位移eff=142.5 mm和等效质量eff=2 802.5 t。
取延性系数=3.0,由式(12)确定等效阻尼比eff= 0.125,将eff,eff,max=0.45和g=0.35代入式(11)确定等效周期eff=2.83 s,由式(8)确定等效刚度eff= 38 kN/mm,再由式(9)确定基底剪力b=5 420 kN。
结构基底剪力达到5 428.3 kN(第202加载步)时的侧移曲线与按“修复后使用”性能水平设计时采用的侧移曲线(式(1))的对比见图9。由图9可知:结构的变形需求小于结构的变形能力,满足8度设防烈度地震下“修复后使用”的性能水平要求。
同时,位于结构底部3层的抗侧力墙板出现了塑性铰(见图10),而钢框架处于弹性阶段,修复和更换墙体后结构仍可使用。

(a) 楼层侧移;(b) 层间位移

图10 第202步时的塑性铰分布
4.3 按“防止倒塌”性能水平校核
按“防止倒塌”性能水平校核,当推覆加载至第450步时,结构的第4层首先达到“防止倒塌”状态的层间位移角限值(=1/50),取相应的推覆曲线做为楼层目标侧移曲线,代入式(6)和(7),计算得到等效单自由度体系的等效位移eff=353.2 mm和等效质量eff= 3 096.5 t。取延性系数=4.5,由式(12)确定等效阻尼比eff=0.146,将eff,eff,max=0.90和g=0.40 s代入式(11)确定等效周期eff=3.27 s,由式(8)确定等效刚度eff= 19.8 kN/mm,再由式(9)确定基底剪力b=6 990 kN。
结构基底剪力达到6 995.4 kN(第450加载步)时的侧移曲线与按“防止倒塌”性能水平设计时采用的侧移曲线(式(1))的对比见图11。由图11可知:结构的变形需求小于结构的变形能力,满足8度罕遇地震下“防止倒塌”的性能水平要求。
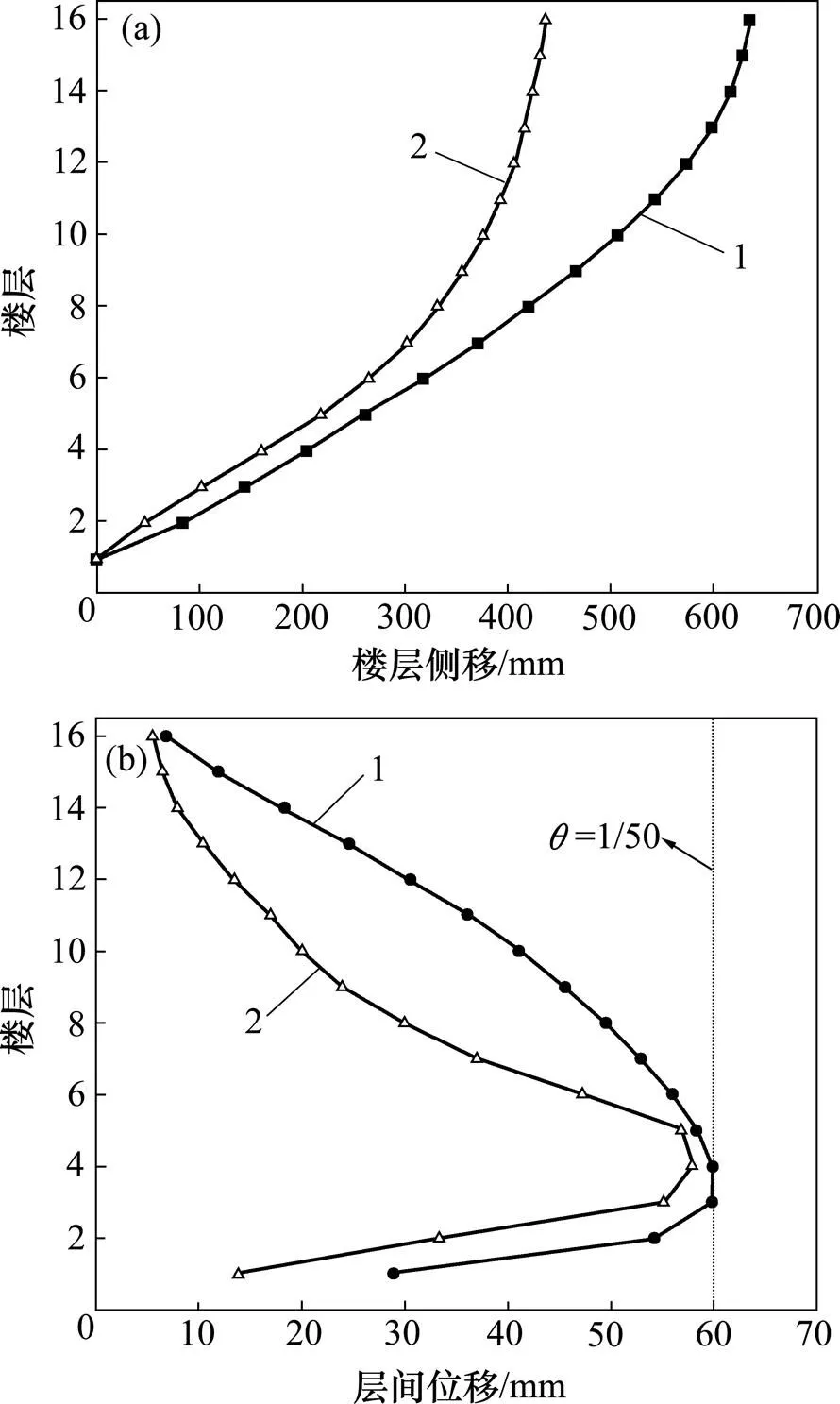
(a) 楼层侧移;(b) 层间位移
图12所示为第450步时的塑性铰分布。同时,抗侧力墙板和框架梁端出现了大量的塑性铰(见图12),而框架柱端出现塑性铰很少,结构不会倒塌。

图12 第450步时的塑性铰分布
5 结论
1) 钢框架−钢筋混凝土抗侧力墙结构是一种典型的双重抗侧力体系,加载过程呈现出明显的两阶段性。抗侧力墙板作为结构体系的第1道防线,在加载前期承担主要的水平荷载,钢筋混凝土墙体发生连接型破坏。随着墙体逐步退出工作,水平荷载向钢框架转移,钢框架成为结构的第2道防线。
2) 对SPW双重抗侧力体系的抗震性能水平及性能指标的量化进行探索研究,在试验研究的基础上,总结分析结构的破坏顺序和破坏形态,提出5个性能水平的失效判别标准,并给出不同性能水平对应的侧移角限值建议。
3) 提出了SPW结构体系直接基于位移的抗震性能设计方法,结合其特点给出了具体的设计步骤,并通过算例给出了16层SPW结构在多遇地震、设防烈度地震和罕遇地震作用下的性能设计过程。
参考文献:
[1] 赵伟, 童根树, 杨强跃. 钢框架内填预制带竖缝钢筋混凝土剪力墙抗震性能试验研究[J]. 建筑结构学报, 2012, 33(7): 141−146. ZHAO Wei, TONG Genshu, YANG Qiangyue. Experimental study on seismic behavior of steel frame with prefabricated reinforced concrete infill slit shear walls[J]. Journal of Building Structures, 2012, 33(7): 141−146.
[2] 彭晓彤, 顾强. 钢框架内填钢筋混凝土剪力墙混合结构破坏机理及塑性分析[J]. 工程力学, 2011, 28(8): 56−61.PENG Xiaotong, GU Qiang.The failure mechanism and plastic analysis of composite steel frame-reinforced concrete infill wall structures[J]. Engineering Mechanics, 2011, 28(8): 56−61.
[3] JU Rueyshyang, LEE Hungien, CHEN Chengcheng, et al. Experimental study on separating reinforced concrete infill walls from steel moment frames[J]. Journal of Constructional Steel Research, 2012, 71(4): 119−128.
[4] HITAKA T, MATSUI C. Experimental study on steel shear wall with slits[J]. Journal of Structural Engineering, ASCE, 2003, 129(5): 586−594.
[5] 周天华, 吴函恒, 白亮, 等. 钢框架−预制混凝土抗侧力墙装配式结构体系[J]. 建筑科学与工程学报, 2013, 30(3): 1−6. ZHOU Tianhua, WU Hanheng, BAI Liang, et al. Fabricated structural system of steel frame-prefabricated concrete lateral resistance wall[J]. Journal of Architecture and Civil Engineering, 2013, 30(3): 1−6.
[6] 周天华, 吴函恒, 白亮, 等. 钢框架−型钢混凝土抗侧力墙装配式结构抗震性能试验研究[J]. 建筑结构学报, 2014, 35(7): 131−137. ZHOU Tianhua, WU Hanheng, BAI Liang, et al. Experimental study on seismic behavior of steel frame-steel reinforced concrete lateral force resisting wall fabricated structures[J]. Journal of Building Structures, 2014, 35(7): 131−137.
[7] 周天华, 吴函恒, 陈军武, 等. 钢框架−预制混凝土抗侧力墙结构抗震性能试验研究[J]. 建筑结构学报, 2015, 36(6): 29−34. ZHOU Tianhua, WU Hanheng, CHEN Junwu, et al. Experimental study on seismic behavior of steel frame-concrete lateral force resisting wall fabricated structures[J]. Journal of Building Structures, 2015, 36(6): 29−34.
[8] 周天华, 管宇, 吴函恒, 等. 钢框架−预制混凝土抗侧力墙装配式结构竖向受力性能研究[J]. 建筑结构学报, 2014, 35(9): 27−34. ZHOU Tianhua, GUAN Yu, WU Hanheng, et al. Research on vertical mechanical behavior of steel frame-prefabricated concrete lateral resistance wall fabricated structures[J]. Journal of Building Structures, 2014, 35(9): 27−34.
[9] GB 50011—2010, 建筑抗震设计规范[S]. GB 50011—2010, Code for seismic design of buildings[S].
[10] JGJ/T 101—2015, 建筑抗震试验方法[S]. JGJ/T 101—2015, Specification of testing methods for earthquake resistant building[S].
[11] FEMA 356/November 2000, Prestandard and commentary for the seismic rehabilitation of buildings[S].
[12] 吴函恒. 钢框架−预制混凝土抗侧力墙装配式结构体系受力性能研究[D]. 西安: 长安大学, 2014. WU Hanheng. Mechanical behavior research on steel frame-prefabricated concrete lateral resistance wall fabricated structural[D]. Xi’an: Chang’an University, 2014.
[13] MIRANDA E, GARCIA J G. Evaluation of approximate methods to estimate maximum inelastic displacement demands[J]. Earthquake Engineering and Structural Dynamics, 2002(31): 539−560.
(编辑 陈爱华)
Performance-based seismic design method of steel frame-concrete lateral resistance wall fabricated structures
WU Hanheng1, ZHOU Tianhua1, CHEN Junwu1, 2, LÜ Jing1
(1.School of Civil Engineering, Chang’an University, Xi’an 710061, China;2.Shaanxi Design and Research Institute of Nonferrous Architectures Co., Ltd, Xi’an 710054, China)
In order to research the performance-based seismic design method of steel frame-concrete lateral force resisting wall fabricated structures, four full scale specimens were tested under the cyclic horizontal load. Seismic performance levels and quantitative index of SPW system were analyzed; failure criteria of five performance levels was put forward, and storey drift ratio limitation for the five performance levels was suggested. The performance-based seismic design method and procedure of SPW system were proposed for SPW system, and the design process was presented through the example of 16-storey SPW system. Experimental results show that the structure is a kind of typical double lateral force resisting system. The concrete lateral force resisting wall is the first line of defense for the structural system, and the steel frame is the second line of defense.
steel frame; concrete lateral resistance wall; fabricated structure; seismic performance index; design method
10.11817/j.issn.1672-7207.2016.11.032
TU398.2
A
1672−7207(2016)11−3852−09
2016−01−25;
2016−03−28
国家自然科学基金资助项目(51508029);中国博士后科学基金资助项目(2015M580802);中央高校基本科研业务费专项资金资助项目(310828161011) (Project(51508029) supported by the National Natural Science Foundation of China; Project(2015M580802) supported by the Postdoctoral Science Foundation of China; Project(310828161011) supported by the Fundamental Research Funds for the Central Universities)
吴函恒,博士,讲师,从事钢结构、钢—混凝土组合结构研究;E-mail: wuhanheng@163.com

