2种锚杆耦合支护的喷混凝土力学模型

李涛，吴爱祥，韩斌，王少勇



2种锚杆耦合支护的喷混凝土力学模型

李涛，吴爱祥，韩斌，王少勇

(北京科技大学土木与资源工程学院，北京，100083)

为确定混凝土层受破坏时中性层的位置并探究不同支护方式下锚喷支护参数与围岩自承能力间的关系，以弹性力学理论为手段，分别将湿喷+管缝式锚杆与湿喷+树脂锚杆耦合支护视为简支梁与固支梁模型，得出这2种耦合支护模型的数学解析式；用数值方法得出混凝土层受破坏时中性层偏离质心的位移计算公式；结合莫尔−库仑准则得出巷道围岩自承能力与锚杆间距、混凝土喷层厚度及混凝土强度之间的力学模型；推导得出喷层厚度每增加10 mm，湿喷+管缝式锚杆与湿喷+树脂锚杆模型中岩体自承能力最高分别提高0.01 MPa与0.40 MPa，喷射混凝土的抗拉强度与围岩破坏所需最大主应力间大致呈线性关系，进而为合理优化巷道支护参数提供依据。

锚喷支护；树脂锚杆；中性层；力学模型

岩土锚固技术是近代岩土工程领域的重要组成部分，作为主动支护形式的一种，它能最大限度地保持围岩的完整性和稳定性，充分发挥围岩自身的支撑作用，对于控制围岩变形、位移及裂隙发育有着重要作用[1−3]。湿喷混凝土与树脂锚杆耦合支护在提高巷道支护效果、保证巷道安全方面效果显著，高刚度、高强度和高可靠性已成为锚杆支护技术的发展趋势[4]。目前，国内外对锚喷支护作用已有较多研究，并取得一定成果[5−13]，但由于岩土工程自身的复杂性，并没有对喷射混凝土层受破坏时中性层的位置及锚喷支护参数与围岩自承能力间的相互作用机理进行定性描述。为此，本文作者以弹性力学理论为研究手段，分别对湿喷混凝土与管缝式锚杆和树脂锚杆这2种不同的耦合支护方式进行力学建模，并结合莫尔−库仑岩体破坏准则对这2种支护方式下喷射混凝土的稳定性进行比较，以便为探究混凝土层破坏作用及合理确定锚喷支护参数提供参考。

1 不同锚杆类型的锚喷支护力学模型

喷射混凝土与锚杆在锚喷支护过程中共同对围岩产生支护效应，由于不同类型锚杆的锚固力相差较大，因而针对不同类型的锚喷支护需要分别建立力学模型：管缝式锚杆的锚固力为100 kN左右，不能有效抵抗岩体的变形移动，此时，可以用简支梁力学模型来解析锚喷支护的力学模型；而树脂锚杆锚固力大，一般在200 kN以上，锚杆托盘可将喷射混凝土层紧贴巷道岩面，树脂锚杆间的喷射混凝土可简化为以锚杆为支点的固支梁力学模型。

1.1 基于管缝式锚杆的锚喷支护力学模型

由于力的相互作用原理，锚固支护时巷道表面围岩会对喷射混凝土层产生反向作用力，在此视为均布载荷。为便于对混凝土层力学模型进行分析，进行如下假设：1) 视锚杆为支点，锚杆间混凝土层为连续、均质、各向同性、符合弹性力学假设条件的梁；2) 喷射混凝土层在屈服破坏之前满足本构方程(其中，为应力，为弹性模量，为应变)； 3) 作用于混凝土层的水平应力较小，因此，水平应力对混凝土层的弯曲影响不大，故在此水平应力忽略不计。由于管缝式锚杆锚固力与树脂锚杆的锚固力相比较低，因此，略去梁两端的边界约束，近似简支。根据上述假设，建立如图1所示的力学模型并进行应力计算。

图1不考虑自重的锚喷支护简支梁力学模型

将式(1)代入应力公式并对积分，得

(2)

其中：，，…，均为常数。利用模型的对称性及上、下2边的主要边界条件：

1.2 基于树脂锚杆的锚喷支护力学模型

图2所示为湿喷+树脂锚杆耦合支护的固支梁力学模型。对其进行力学建模时不能直接应用半逆解法进行求解，需要先对固支梁力学模型进行分解，如图3所示。分别对图3(a)和图3(b)进行应力分量求解，这2部分分量之和即为整个固支梁模型的应力分量。

对图3(a)所示模型进行应力函数求解，得

图2 不考虑自重的锚喷支护固支梁力学模型

(a) 考虑均布载荷作用；(b) 考虑弯矩与剪力作用

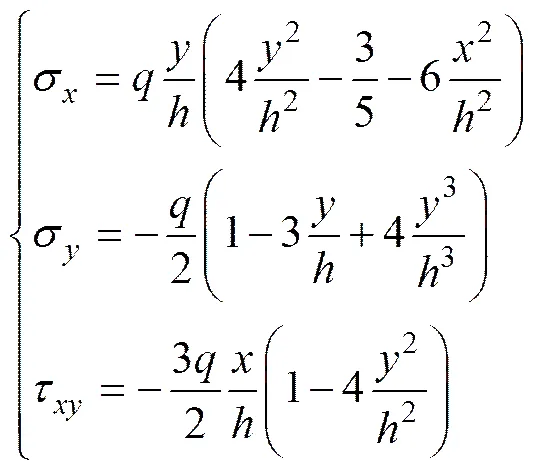
同理，对图3(b)所示模型进行应力函数求解，得应力分量：

(6)

将式(5)和(6)联立可得

应力分量中包含弯矩和剪力s共2个待定系数，根据二次静不定结构的特点利用位移边界条件进行求解。考虑应变分量的物理方程

，，

及几何方程

，，(9)

将式(7)和式(9)中的各应力分量代入式(8)，得

积分后代入式(9)中的第3式，得

式(11) 2边分别为和的函数，设2边都等于相同的常数，则

式中：0，0和均为表征刚体位移的常数。根据固支梁模型假设知，模型具有对称性，且固定端的边界中点近似为完全固定不动，由位移约束条件

2 混凝土层受破坏时中性层位置的确定

混凝土层在受力变形的过程中，必定存在拉伸区和压缩区的分界面即中性层。对于中性层的位置，有的认为其存在于混凝土层的质心处[5]，但在实际条件下，中性层会发生上移而偏离中心位置。这是由于混凝土类材料在应力达到一定值后，拉应力−拉应变之间的曲线并不呈线性关系[14−15]，当梁边沿拉应力超过材料的抗拉强度时，该处不是先产生弹性断裂，而是发生塑性屈服。由于混凝土材料的抗压强度远大于其抗拉强度，最终破坏是由拉力区的过度变形引起拉伸破坏，为保持梁的平衡，其中性轴会在受力过程中逐渐上移而偏离中心位置。以上为材料力学解释，下面以简支梁为例对混凝土层受破坏时中性层的偏移情况进行数值求解。假定在混凝土中间截面的形心处(=0，=0)，水平位移为0，而铅直位移等于挠度，则由式(4)得

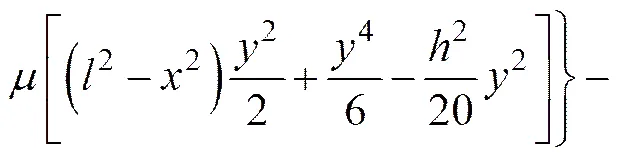
由的表达式可见混凝土层的中性层并不在中线处。假定混凝土层的截面在弯曲时保持为平面且两端()挠度为0，则由的表达式得挠度曲线方程：

对挠度曲线方程进行的二次求导，可求得曲率的表达式：

3 支护参数与提高围岩自承能力的关系

在围岩中布置锚杆与喷射混凝土等都是以约束坑道周边位移来实现其支护作用。锚喷支护后，围岩会在应力场的作用下发生变形，在围岩变形过程中，锚杆主要起支撑和约束作用。根据式(4)和式(11)中的计算公式可知，这2种支护方式的最大拉应力均在，处，即

为寻求喷射混凝土厚度、喷射混凝土强度及锚杆间距与围岩自承能力间的关系，结合莫尔−库伦强度准则有岩体黏聚力与内摩擦角的关系式：

(14)

式(14)即为锚喷支护参数与围岩自承能力在固支梁与简支梁这2种情况下的关系表达式。

3.1 喷射混凝土厚度

在锚杆间距、混凝土层承受的载荷相同的条件下，根据式(14)可得出2种不同支护方式下混凝土厚度与围岩破坏所需最大主应力的关系曲线，如图4所示。

1—简支梁力学模型；2—固支梁力学模型。

从图4可以看出：

1) 不论湿喷混凝土+树脂锚杆支护还是湿喷混凝土+管缝锚杆支护，随着喷射混凝土厚度的增加，两者都不同程度地提高了岩体所能承受的最大主应力。

2) 湿喷混凝土+树脂锚杆支护模型中，围岩的自承能力随喷射混凝土厚度以指数函数形式增长，喷层厚度每增加10 mm，岩体的自承能力最大可提高 0.4 MPa。而对于湿喷混凝土+管缝锚杆支护，随着喷射混凝土厚度的增加，岩体的自承能力增加不明显，喷射厚度每增加10 mm，岩体的自承能力可增加0.01 MPa。2种支护方式相比较，采用树脂锚杆或高强度锚杆更有利于维持巷道的稳定性。

3.2 喷射混凝土强度

如上所述，根据式(14)可得出混凝土抗拉强度与围岩破坏所需最大主应力关系曲线，如图5所示。由图5可看出：

1) 随着混凝土抗拉强度的增加，固支梁力学模型即湿喷+树脂锚杆耦合支护下的岩体破坏所需最大主应力要比简支梁力学模型的大，但两者相差不大，且均呈线性增加，即岩体承载能力随之增加。

2) 当混凝土抗拉强度由1 MPa增大到5 MPa时，岩体破坏所需的最大主应力提高了0.35 MPa左右，说明为了加强巷道支护作用，可适当提高喷射混凝土 强度。

1—简支梁力学模型；2—固支梁力学模型。

4 工程应用

吉林板庙子矿岩体为构造角砾岩，稳定性较差，采用分段空场嗣后充填采矿法。之前采用的干喷+管缝式锚杆支护具有混凝土强度低、回弹量高、粉尘量大及锚杆锚固力低等缺点。采用湿喷混凝土+树脂锚杆支护，设备主要为Spraymec 1050 WPC湿喷台车及H282双臂液压凿岩台车。主斜坡道断面宽×高为 5.0 m×5.2 m，分段联络道及分段道宽×高为4.6 m× 4.8 m。

通过适当增大湿喷混凝土厚度及混凝土的抗拉强度可提高巷道围岩的自承能力。板庙子金矿原支护参数为锚杆长度为2.4 m，锚杆间距为1.2 m，排距为 2.0 m，干喷厚度为60.0 mm，新支护参数为锚杆间距为 1.0~1.2 m，排距为1.2 m，湿喷混凝土厚度增加到75.0~100.0 mm。使用新的支护工艺后，采用标准法进行湿喷混凝土的强度检测：将搅拌好的料浆均匀装入长×宽×高为100 mm×100 mm×100 mm试模，48 h脱模后养护至28 d，进行单轴抗压强度测试。测试结果的平均值为30 MPa，明显高于干喷混凝土强度。另外，利用ZY−20型锚杆拉拔计进行树脂锚杆拉拔试验，锚固力试验结果为150~190 kN，说明树脂锚杆有较好的锚固效果。在正常情况下其锚固力都能大于150 kN，锚固强度比管缝式锚杆提高120 kN左右，有利于围岩的稳定，说明湿喷+树脂锚杆耦合支护模型具有良好的适用性。

5 结论

1) 分别将湿喷+管缝式锚杆与湿喷+树脂锚杆耦合支护视为简支梁和固支梁模型，可得出这2种耦合支护模型的合理数学解析式。

2) 用数值方法求解出混凝土层在受破坏过程中中性层偏离质心的位移计算公式，并推导出混凝土层受力变形时的挠度曲线方程和曲率表达式。

3) 结合莫尔−库仑强度准则，分别得出2种支护方式下不同支护参数与围岩自承能力间的关系表达式，进而可据数学解析式对两者进行对比分析。

4) 湿喷混凝土+树脂锚杆支护模型中，围岩的自承能力随着喷层厚度的增加幅度较大，喷层厚度每增加10 mm，岩体的自承能力最大可提高0.4 MPa，而湿喷混凝土+管缝锚杆支护则仅最大提高0.01 MPa。故采用树脂锚杆或高强度锚杆更利于维持巷道的稳 定性。

5) 喷射混凝土的抗拉强度与围岩破坏所需最大主应力间大致呈线性关系，采用高强度的湿喷混凝土技术能明显减少冒落事故。

参考文献：

[1] 姚爱敏, 孙世国, 刘玉福. 锚杆支护现状及其发展趋势[J]. 北方工业大学学报, 2007, 19(1): 91−94. YAO Aimin, SUN Shiguo, LIU Yufu. Present situation and development trend of bolt support[J]. Journal of the Northern Industrial University, 2007, 19(1): 91−94.

[2] 张连福. 新型锚喷支护技术及其在桃园矿区的应用[J]. 岩石力学与工程学报, 2006, 25(11): 2208−2212. ZHANG Lianfu. New technology of bolted shotcrete support and its application to Taoyuan coal mine[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(11): 2208−2212.

[3] AKISANYA A R, IVANOVIĆ A. Debonding along the fixed anchor length of a ground anchorage[J]. Engineering Structures, 2014, 74: 23−31.

[4] ALI A, ABADLLA J, HAWILEH R, et al. CFRP mechanical anchorage for externally strengthened RC beams under flexure[J]. Physics Procedia, 2014, 55: 10−16.

[5] 王少勇, 吴爱祥, 韩斌, 等. 湿喷混凝土+树脂锚杆耦合支护的力学模型[J]. 中南大学学报(自然科学版), 2013, 44(8): 3486−3492. WANG Shaoyong, WU Aixiang, HAN Bin, et al. Wet shotcrete and resin bolt coupling mechanics model[J]. Journal of Central South University (Science and Technology), 2013, 44(8): 3486−3492.

[6] FEYS D, VERHOEVEN R, DE SCHUTTER G. Fresh self compacting concrete, a shear thickening material[J]. Cement and Concrete Research, 2008, 38(7): 920−929.

[7] LI T, BROWN E T. Dynamic capable ground support development and application[C]// Proc 5th Int Symp Ground Support in Mining & Underground Construction. Perth, 2004: 28−30.

[8] GUO Zhibiao, YANG Xiaojie, BAI Yunpeng. A study of support strategies in deep soft rock: the horsehead crossing roadway in Daqiang Coal Mine[J]. International Journal of Mining Science and Technology, 2012, 22(5): 665−667.

[9] CAI Yue, ESAKI T, TIANG Yujing. An analytical model to predict axial load in grouted rock bolt for soft rock tunneling[J]. Tunnelling and Underground Space Technology, 2004, 19(6): 607−618.

[10] NELSON C R. Spray grouting for tunnel support and lining[J]. Underground Space, 1977, 14(5): 241−246.

[11] PICKELMANN J, PLANK J. A mechanistic study explaining the synergistic viscosity increase obtained from polyethylene oxide (PEO) and-naphthalene sulfonate (BNS) in shotcrete[J]. Cement and Concrete Research, 2012, 42(11): 1409−1416.

[12] MALMGREN L, NORDLUND E, ROLUND S. Adhesion strength and shrinkage of shotcrete[J]. Tunnelling and Underground Space Technology, 2005, 20(1): 33−48.

[13] LEUNG C K Y, LAI R, LEE A Y F. Properties of wet-mixed fiber reinforced shotcrete and fiber reinforced concrete with similai composition[J]. Cement and Concrete Research, 2005, 35(4): 788−795.

[14] 姜福田. 混凝土力学性能与测定[M]. 北京: 中国铁道出版社, 1989: 109. JIANG Futian. Mechanical properties of concrete and determination[M]. Beijing: China Railway Press, 1989: 109.

[15] 唐礼忠, 彭续承. 尾砂胶结充填体变形及强度试验研究[J]. 中南工业大学学报(自然科学版), 1996, 27(2): 145−148. TANG Lizhong, PENG Xucheng. Research on backfilling consolidated filling body deformation and strength[J]. Journal of Central South University of Technology (Natural Science), 1996, 27(2): 145−148.

(编辑 陈灿华)

Mechanical models of wet shotcrete with two kinds of bolt coupling support

LI Tao, WU Aixiang, HAN Bin, WANG Shaoyong

(School of Civil & Environment Engineering, University of Science & Technology, Beijing, Beijing 100083, China)

In order to determine the position of the neutral layer when the concrete layer is in failure, and explore the relationship between parameters of bolt-shotcrete support and surrounding rock self-supporting capacity under different ways of support, the mathematic analysis of this two coupling support models was obtained by means of elastic mechanics theory, with wet shotcrete pluses slotted tube bolt and resin bolt being regarded as beam and fixed-end beam, respectively. The neutral layer displacement formula of deviating from the center of mass were obtained by using numerical method. Combined with Mohr−coulomb criterion, the mechanical model of the bolt spacing, the shotcrete layer thickness and strength to surrounding rock self-supporting capacity was obtained. The results show that surrounding rock self- supporting capacity increases up to 0.01 MPa and 0.40 MPa in resin wet shotcrete pluses slotted tube bolt and resin bolt respectively when shotcrete layer thickness increases every 10 mm, and there is approximately linear relationship between tensile strength of shotcrete and the desired maximum principal stress of rock damage, which provides basis for the reasonable roadway supporting parameters optimization.

bolt-shotcretesupport; resin bolt; neutral layer; mechanical model

10.11817/j.issn.1672-7207.2016.11.031

TD35

A

1672−7207(2016)11−3846−06

2015−11−12；

2016−01−15

国家“十二五”科技支撑计划项目(2012BAB08B02，2013BAB02B05) (Projects(2012BAB08B02，2013BAB02B05) supported by the State “Twelfth Five-year” Science and Technology Support Plan)

吴爱祥，教授，从事采矿与岩石力学研究；E-mail: 1604598578@qq.com