关于秩-3矩阵的Yang-Baxter 型矩阵方程的交换解*

周端美，丁佳文

(赣南师范大学 数学与计算机科学学院，江西 赣州 341000)



·计算方法·

关于秩-3矩阵的Yang-Baxter 型矩阵方程的交换解*

周端美，丁佳文

(赣南师范大学 数学与计算机科学学院，江西 赣州 341000)

令A是一个特征值为0，秩为3的矩阵，本文给出矩阵方程AXA=XAX的所有交换解.

Yang-Baxter矩阵方程； Jordan标准型；秩

1 引言

在1967年12月，杨振宁教授发表了一篇关于简单一维多体问题的论文[1]，并引入方程

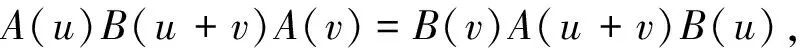
(1)

其中A和B是有理函数.5年后，R. J. Baxter在研究一些经典二维统计力学问题时同样独立给出了这个方程[2].之后这方程被定义为Yang—Baxter Equation (YBE).由 (1) 式，还导出了不同形式的YBE.设V是复向量空间，R(u)是u∈C的取值于Endc(V⊗V)中的函数.关于R(u)的下述方程就称为YBE：

R12(u)R13(u+v)R23(v)=R23(v)R13(u+v)R12(u)

这里Rij表示V⊗3的如下的矩阵：它作用在第i个与第j个分量上相当于R(u)，作用在另一个分量上相当于恒等映射；例如R23(u)=I⊗R(u)，变量u称为谱参数.(1) 式的解常常称作R矩阵.

自从YBE由杨振宁(1967)[1]和巴克斯特(R. J. Baxter1972)[2]分别独立引入到物理学中，它一直是作为统计力学与量子场论中可积模型的主要方程在研究.在其它领域，如C*-代数，环链不变量，量子群和保形场论等也有很多应用[3-7]，这使YBE的重要性更加突出，并引起了许多人的兴趣.近年来，研究者发现YBE和量子信息、拓扑量子计算有着紧密的联系.随着量子信息和量子计算的快速发展，量子信息理论被当作一种重要的物理资源引起越来越多的关注.从而YBE 及其相关的数学物理性在近几年已成为理论物理和数学物理研究领域的前沿分支之一，它包含了极为丰富的物理内容.借助幺正的YBE来研究量子纠缠、量子信息传输以及拓扑量子计算成为了比较热门的研究课题.该分支领域的研究极大的丰富了以YBE为中心的理论.然而，这样一个简单的矩阵方程却还没有在矩阵论中得到很好的研究[8-14].下面我们把YBE (1) 做一些限制性条件，从而转化成更简单的矩阵方程.

如果A和B关于u和v都是独立的，则YBE (1) 化简成

(2)

则称(2)为Yang—Baxter矩阵方程(YBME).要找到所有满足矩阵方程(2)的矩阵对(A,B)并不是一件简单的工作.在两个n×n矩阵A和B中固定一个矩阵，如固定A，找满足矩阵方程(2)的B等价于求解一个n2个未知数，n2个二次方程的方程组.多项式方程系统的解是代数几何的一个主要的热点问题，要找到所有的解并不是一件容易的事，即使是3×3的矩阵[8].本文的目的：当A是特征值为0,秩为3矩阵时，找到所有满足(2)式的可交换矩阵对(A,B).因此，我们假定矩阵A已知，解下面方程

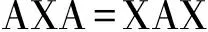
(3)

中的矩阵X.A为任意矩阵时， X=0和X=A都是方程(3)的解，所以要解的是这两个平凡解之外其他的解.以下如无特别声明，都指非平凡解.YBME(3)作为二次方程，方程有无穷多解.

当A任意时，令A的Jordan分解为

(4)

再令Y=W-1XW,则由AXA=XAX可得JYJ=YJY,由于需要找矩阵方程AXA=XAX的交换解，即满足AX=XA，由此可得JY=YJ.反过来说，如果J=W-1AW，Y=W-1XW满足JYJ=YJY和JY=YJ，那么A和X就满足AXA=XAX和AX=XA.所以求解交换解X可求解

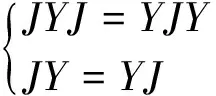
(5)

这个矩阵方程组，然后再用X=WYW-1回代求出最终的交换解.

因为矩阵A的特征值为0，且秩为3，所以它的相似Jordan矩阵J满足下面两个条件：

2 当Λ=Λ1时YBME的所有交换解

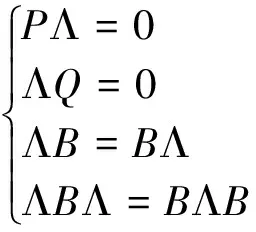
(6)

在这一部分，假设J=diag(0,Λ1)，即Λ=Λ1.另外两种情况J=diag(0,Λ2)和J=diag(0,Λ3)将分别在第3和第4部分进行研究. 因为方程组(6)中最后一个方程ΛBΛ=BΛB本身就是一个YBME，为求YBMEJYJ=YJY的所有交换解，可先求解矩阵方程ΛBΛ=BΛB的所有交换解，即求解矩阵方程组

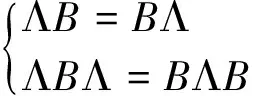
(7)

由此可得b21=b32=b31=b42=b41=b43=0，b11=b22=b33=b44，b12=b23=b34,b13=b24.所以，

(8)

再由矩阵方程组(7)中ΛBΛ=BΛB知

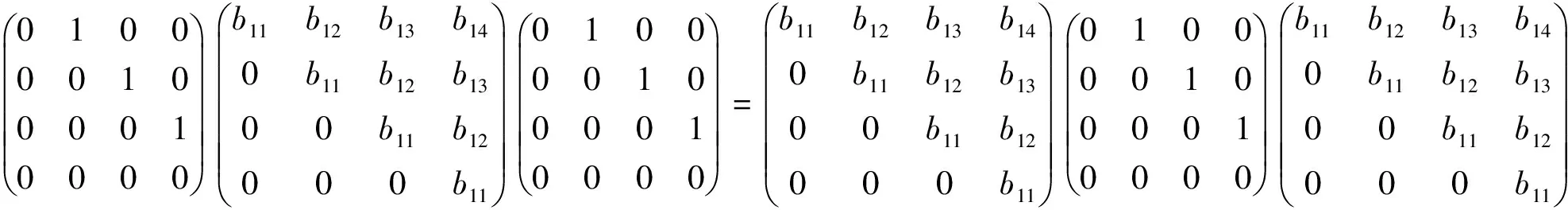
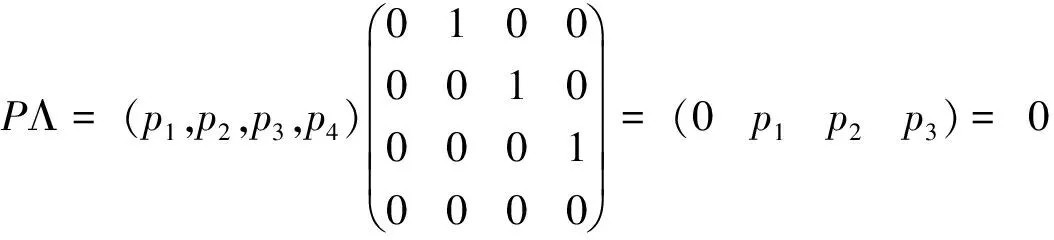
可得q2=q3=q4=0.因为M,p4,q1在方程中始终未出现，所以它们为任意量.由引理1知，当B=B1时，

3 当Λ=Λ2时YBME的所有交换解

在这一部分，本文给出在Λ=Λ2时，YBME(3)的所有交换解，即求解矩阵方程组(6).

引理2 当Λ=Λ2时，矩阵方程组(7)关于B的解为

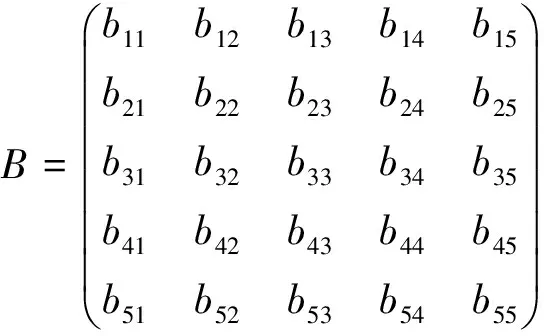
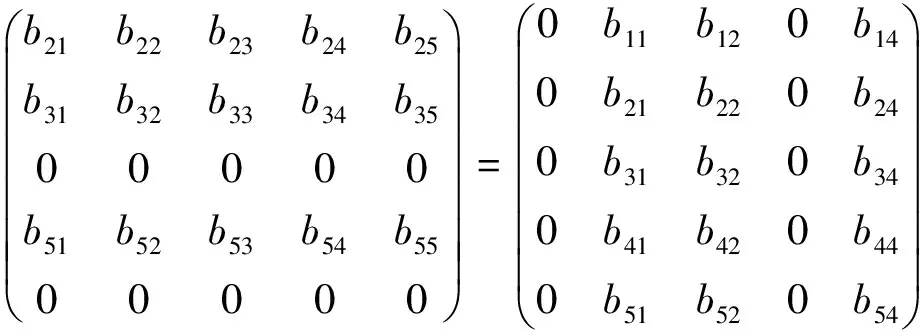
(9)

由此知b11=0，b44=0，b14=0，b42任意；或b11=0，b44=0，b42=0，b14任意.将b11,b44,b14,b42代入(9)可得B的解.证毕.

定理2 当Λ=Λ2时，YBME(3)的所有交换解为X=WYW-1,

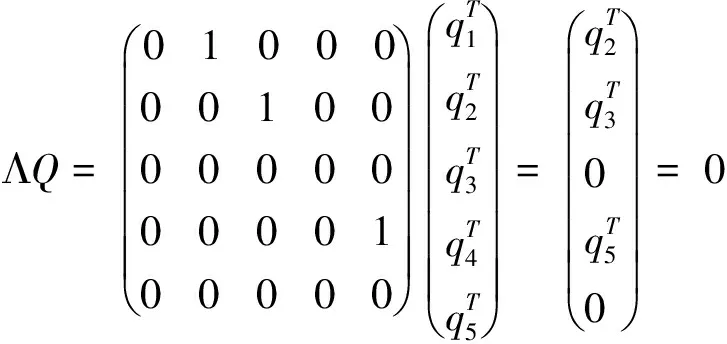
证毕.

4 当Λ=Λ3时YBME的所有交换解

在这一部分，给出Λ=Λ3这种情况下，矩阵方程组(6)的解.

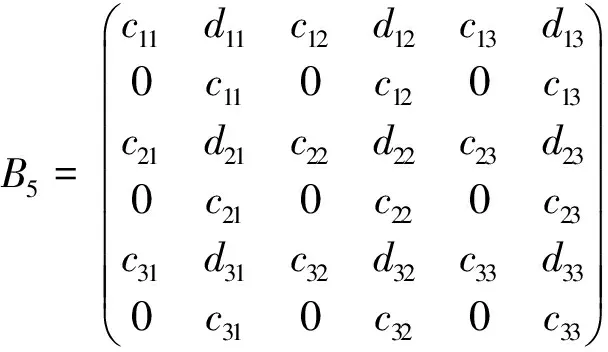
则C2=0.

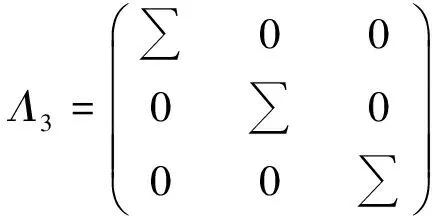
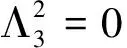
定理3 当Λ=Λ3时，YBME(3)的所有交换解为X=WYW-1,

5 数值例子

在这一部分我们将根据J=diag(0,Λ1)和J=diag(0,Λ2)两种情况分别给出两个例子.

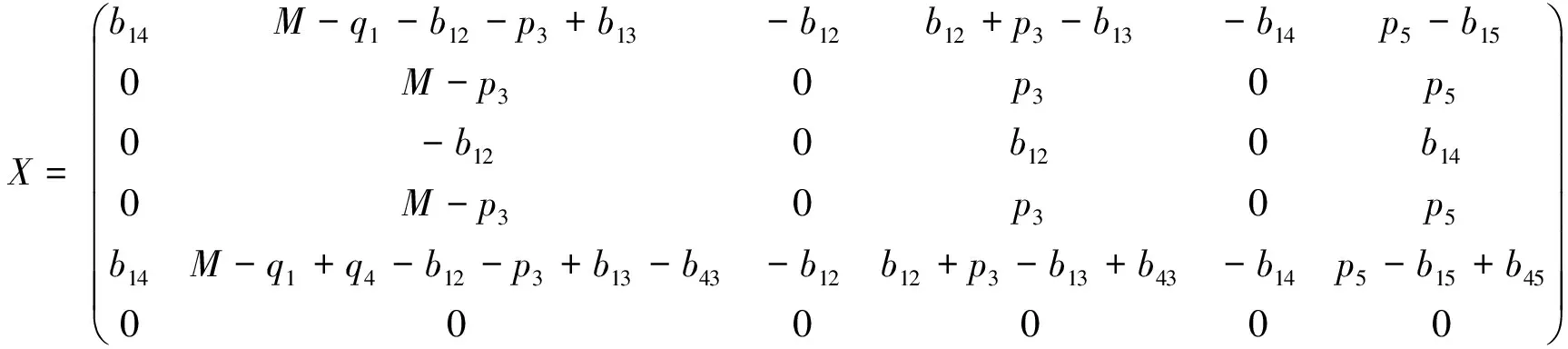
6 结论

当A是一个秩为3，特征值为0的矩阵时，本文给出了YBME(3)的所有交换解.本文所采用的方法是先找出A的Jordan标准型，用A的Jordan标准型代替A，从而得到一个简化的YBME.根据A的Jordan标准型的不同形式，解出其相应的交换解，再回代最终得到YBME(3)的所有交换解.虽然不能用代数几何方法找到YBME(3)的所有解，但在一些特殊情况下，本文找到了一部分解.

[1] C. N. Yang. Some exact results for the many-body problem in one dimension with repulsive delta-function interaction[J].Phys. Rev. Lett,1967,19:1312-1315.

[2] R.J.Baxter. Partition function of the eight-vertex lattice model[J].Ann.Phys,1972,70:193-228.

[3] M. Atiyah. Geometry, topology and physics[J].Quart. J. Roy. Astr. Soc,1988,29:287-299.

[4] L.D. Faddeev. History and perspectives of quantum groups[J].Milan J. Math.,2006,74:279-294.

[5] F. Felix, Nonlinear Equations, Quantum Groups and Duality Theorems: A Primer on the Yang-Baxter Equation[M].VDM Verlag,2009.

[6] M. Jimbo. Introduction to the Yang-Baxter Equation[M].Braid Group, Knot Theory and Statistical Physics II, World Scientic,1994:153-176.

[7] C. Yang, M. Ge. Braid Group, Knot Theory, and Statistical Mechanics[M].World Scientific,1989.

[8] A. Cibotarica, J. Ding, J. Kolibal, N. Rhee.Solutions of the Yang-Baxter matrix equation for an idempotent[J].Numer. Algb., Control, Optim., 2013,3(2):235-245.

[9] J. Ding and N. Rhee. A nontrivial solution to a stochastic matrix equation[J].East Asian J. Applied Math., 2012,2:277-284.

[10] J. Ding and N. Rhee. Spectral solutions of the Yang-Baxter matrix equation[J].J. Math. Anal. Appl.,2013,402:567-573.

[11] J. Ding, N. Rhee, C. Zhang. Further solutions of a Yang-Baxter-like matrix equation[J].East Asian J. Applied Math.,2013,2(4):352-362.

[12] J. Ding, N. Rhee, C. Zhang. Commuting solutions of the Yang-Baxter matrix equation[J].Applied Math. Lett., 2015,44:1-4.

[13] J. Ding and C. Zhang. On the structure of the spectral solutions of the Yang-Baxter matrix equation[J].Applied Math. Lett.,2014,35:86-89.

[14] H. Tian. All solutions of the Yang-Baxter-like matrix equation for rank-one matrices[J].Applied Math. Lett.,2016,51:55-59.

Commuting Solutions of the Yang-Baxter Matrix Equation for Rank-Three Matrices

ZHOU Duanmei, DING Jiawen

(SchoolofMathematicsandComputerScience,GannanNormalUniversity,Ganzhou341000,China)

LetAbe a rank 3 matrix with eigenvalues 0. We get all the commuting solutions of the quadratic matrix equationAXA=XAX.

Yang-Baxter Matrix Equation; Jordan Form; Rank

2016-05-26

10.13698/j.cnki.cn36-1346/c.2016.06.001

国家自然科学基金(11501126，11471122)；江西省自然科学基金(20151BAB211011)；江西省教育厅科学技术研究项目(GJJ150979)；中央财政支持地方高校发展专项基金；赣南师范学院大学生创新创业训练计划项目

周端美(1985-),男,赣南师范大学数学与计算机科学学院讲师,博士,研究方向：矩阵方程求解与应用.

http://www.cnki.net/kcms/detail/36.1037.C.20161209.1500.004.html

O151.21

A

1004-8332(2016)06-0001-07