二维TM波时域非连续伽略金算法理论数值通量研究

李林茜 魏兵 杨谦 葛德彪 王飞

(1.西安电子科技大学物理与光电工程学院,西安 710071;2.西安电子科技大学信息感知技术协同创新中心,西安 710071)



二维TM波时域非连续伽略金算法理论数值通量研究

李林茜1,2魏兵1,2杨谦1,2葛德彪1,2王飞1,2

(1.西安电子科技大学物理与光电工程学院,西安 710071;2.西安电子科技大学信息感知技术协同创新中心,西安 710071)

采用数值通量的方式进行场量交互是时域非连续伽略金(Discontinuous Galerkin Time Domain,DGTD)算法区别于时域有限元(Finite Element Time Domain, FETD)方法的主要方面.从二维TM情形弱解方程出发,讨论了当前三角形单元和相邻单元进行场量交互时数值通量物理意义和不同形式.结合数值通量和弱解方程得到了DGTD算法的迭代计算式.给出了线元辐射和双线元干涉的数值算例,算例结果表明了文中方法的正确性.

时域非连续伽略金算法;算法值通量;结点基函数

DOI 10.13443/j.cjors.2015111702

引 言

时域电磁仿真方法因其能够通过一次时域计算结合傅里叶变换即可得到宽频带信息的特点,近年来受到人们广泛关注.时域有限差分(Finite Difference Time Domain, FDTD)方法[1-2]是目前电磁学领域内被人们广泛、深入地研究,并取得巨大成功应用的方法.该方法原理直观、编程简便、实用性强,一直在时域方法中占主导地位.但由于FDTD方法采用规则网格剖分,其建模的能力弱,对弯曲表面的阶梯近似,严重限制了将其应用于复杂几何结构时的计算精度.另外一种时域算法为时域有限元(Finite Element Time Domain, FETD)方法,该算法采用非结构单元拟合(如四面体),与真实目标的差异小.但FETD每一时间步需要求解大型线性方程组,难以处理电尺寸较大目标的电磁问题.

非连续伽略金 (Discontinuous Galerkin,DG) 方法20世纪70年代就应用于偏微分方程的求解,随后，该算法思想被应用于流体力学及时域有限体积(Finite Volume Time Domain, FVTD)法中.近年来,人们基于FETD和FVTD的思想,提出了非连续伽略金时域(Discontinuous Galerkin Time Domain, DGTD)[3-5]算法.DGTD算法既具有有限元方法采用非结构网格对复杂外形拟合好、便于采用高阶基函数和计算精度高的优点,又具有FVTD方法完全显式迭代、计算效率高的优点.在多尺度问题、波导不连续问题等方面广泛的应用前景使得该算法成为近年来计算电磁学界的热点之一.

非连续的核心思想就是放宽单元之间的连续性边界条件,即边界处数值通量[3，6-7]的处理.本文从时域弱解方程出发,着重讨论了数值通量的形成,给出了二维TM波情形的通量表达式.结合数值通量和弱解方程得到了DGTD算法的矩阵方程,离散得到时域步进公式,最后给出了具体算例.

1 二维TM波DGTD算法理论的关键技术:数值通量

二维TM波情形下弱解方程为[8-9]

(1)

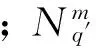
(2)

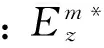
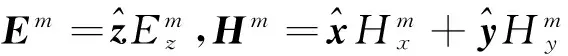
(3)

式(3)代入式(2)得到

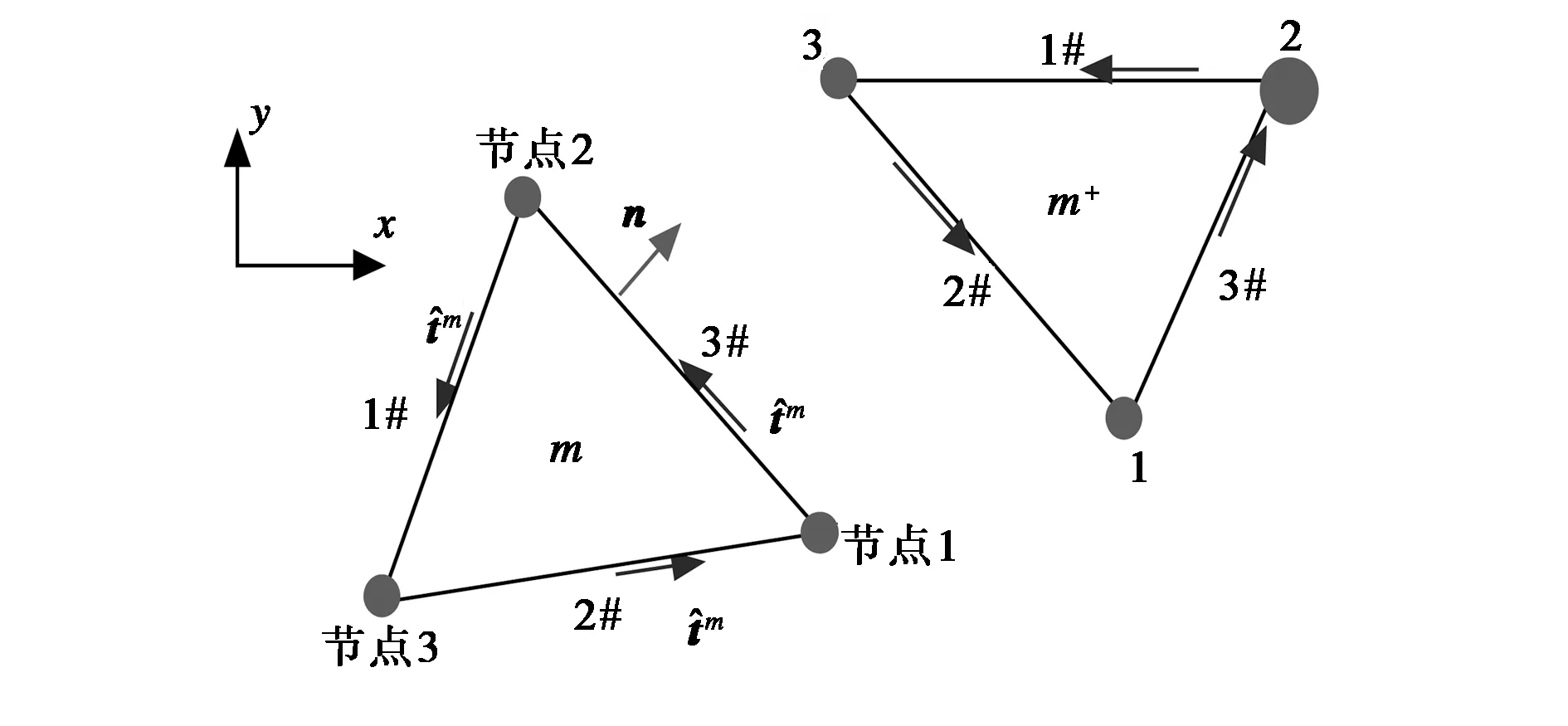
图1 相邻二个三角形单元

(4)

消去单位矢量后式(4)变为

(5)

为了便于应用,将式(5)的第二式拆分为两个独立式，有

(6)

表1给出了DGTD算法中数值通量的三种常见形式[4].若采用中心数值能量(Centered Numerical Flux,CNF)即νh=νe=0,κh=κe=κ=1/2,式(6)变为

(7)

将突变边界条件式(6)代入式(1)得

(8)

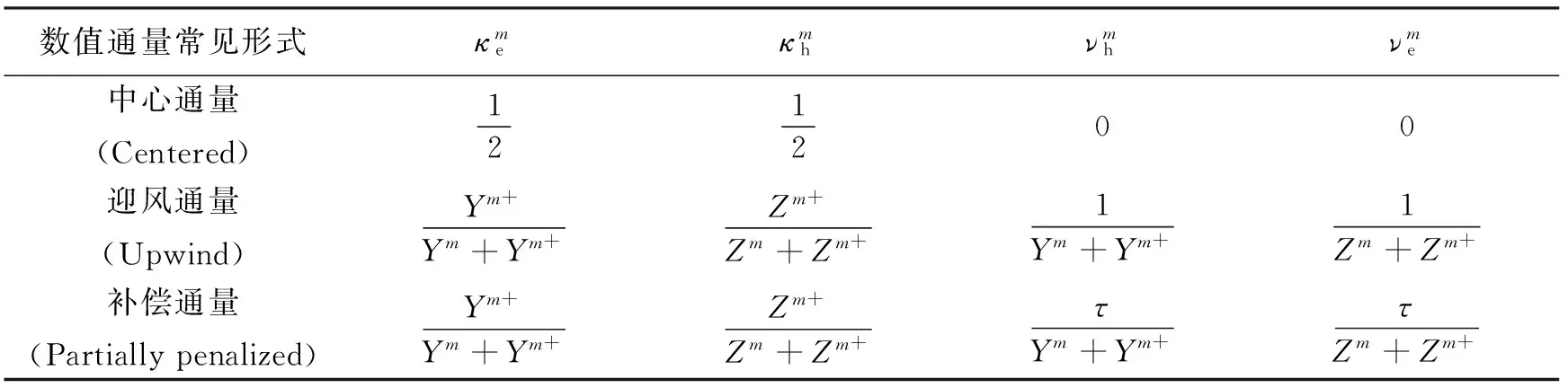
表1 DGTD算法中数值通量的三种常见形式

(9)

将展开基函数式(9)代入式(8)整理后写成矩阵形式:

(10)

(11)

(12)

式中:[Mm],[Sx],[Sy]的元素

以及

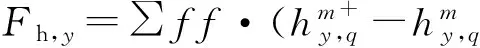
(13)

(14)

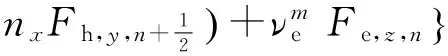
(15)

式中:

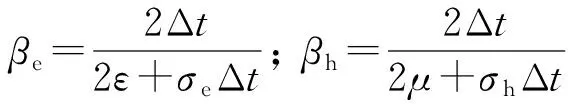
2 数值算例

算例1 线电流源TM波与解析结果的比较.计算域为6m×6m的矩形域,被离散为2 773个结点,5 376个三角形单元.线源设置在计算区域的中心(0m, 0m)处.时谐场频率f=0.15GHz,时间间隔Δt=0.33×10-10s,采用Gedney形式的各向异性完全匹配层(UniaxialPerfectMatchedLayer,UPML)吸收边界.图2(a)是第1 000个时间步的场值快照,图2(b)是二维DGTD算法计算值与利用Hankel函数得到的解析结果的比较.

(a) 第1 000个时间步的场值快照

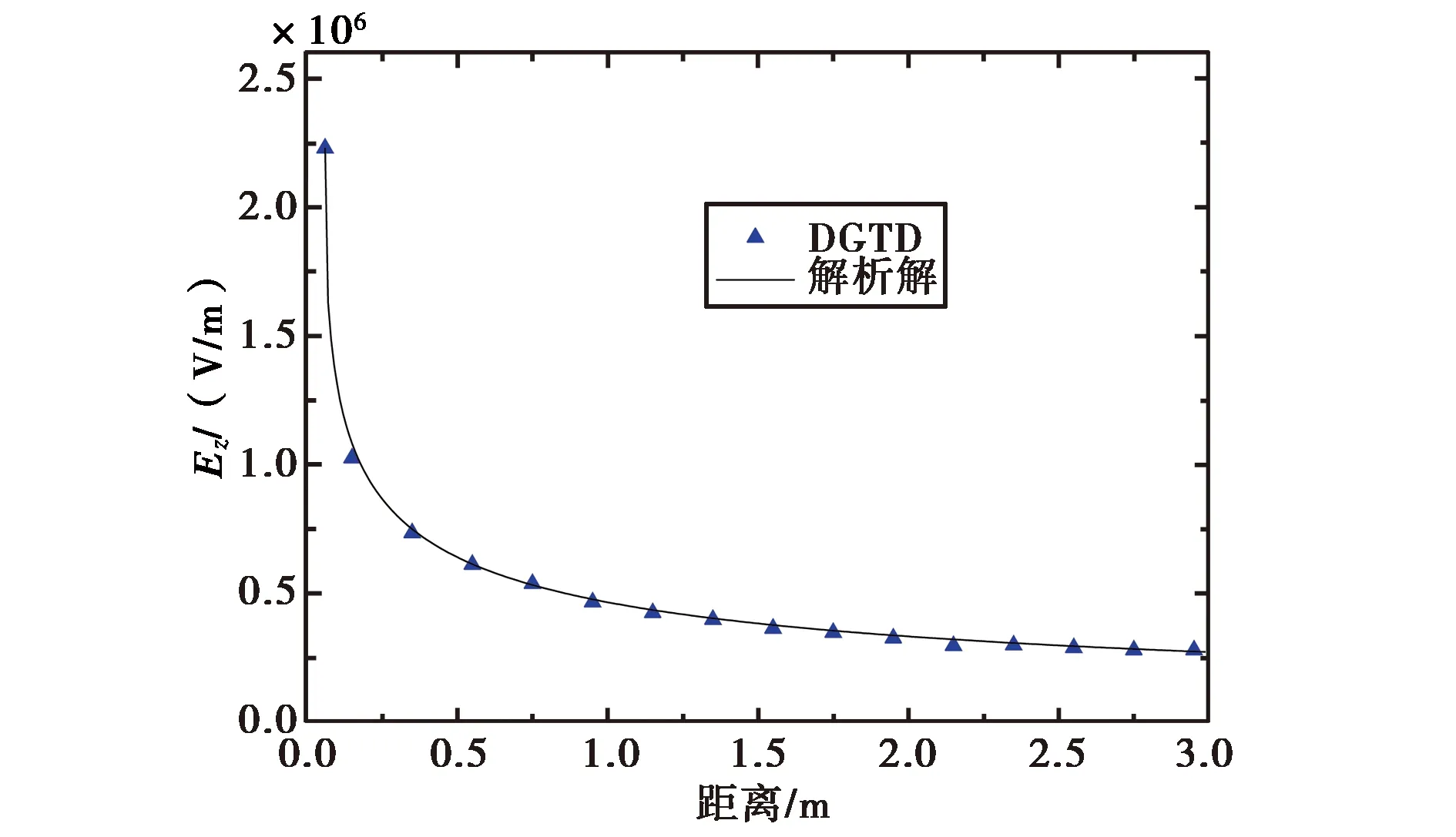
(b) 空间场值分布图2 线电流源在自由空间中的辐射电场

算例2 两个电流源干涉时的近、远场分布.计算域为4m×4m的矩形区域,外推边界边长3m×3m,离散尺度0.1m,共离散为2 736个结点,5 310个三角形单元(如图3(a)所示).电磁波波长1m,Δt=0.416×10-10s两个线源相距半个波长.第200个时间步的场值快照如图3(b)所示,图3(c)是归一化的远区辐射场(圆圈),作为比较图中还给出了解析结果(实线).

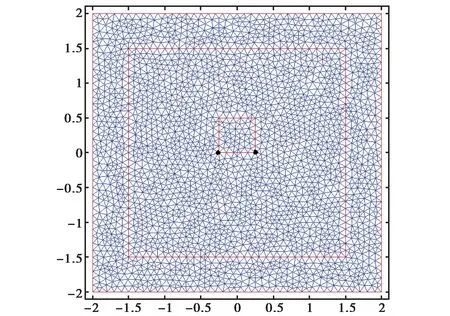
(a) 计算区域示意图

(b) 第200个时间步的场值快照

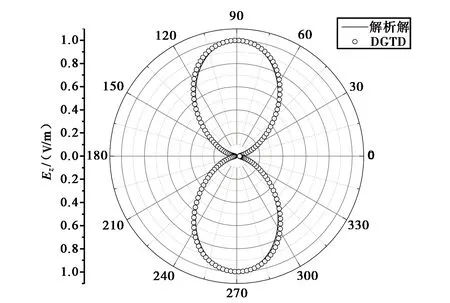
(c) 计算域幅值归一化的远区场值分布图图3 两个线电流源干涉

3 结 论

本文讨论了二维TM情形DGTD算法的实现过程,主要给出了其核心思想数值通量和物理含义及其具体表达式.二维线电流源辐射和双线电流源干涉的算例,表明本文算法的正确有效性.DGTD算法将相邻单元之间的切向连续性关系变为不连续,使将形成的大型矩阵方程变成相邻单元之间相关的显式的小矩阵方程,其求解所需要的内存和时间都远远小于FETD方法,二维情形,如果计算域有n个三角形单元,则有约3n/2个棱边,FETD方法求逆复杂度为O((3n/2)3),而DGTD算法的求逆复杂度为O(33n),因此DGTD算法具有巨大优势.

[1]苏卓, 谭峻东, 张俊, 等.基于高阶时域有限差分算法的电磁波传播计算[J].电波科学学报, 2014, 29(3):431-436.

SUZ,TANJD,ZHANGJ,etal.Anelectromagneticwavepropagatorbasedonhigher-orderFDTDmethod[J].Chinesejournalofradioscience, 2014, 29(3)：431-436.(inChinese).

[2]阎亚丽, 傅光, 龚书喜, 等.基于并行FDTD方法分析表面等离子波导的特性[J].电波科学学报, 2015, 30(4)：668-672.

YANYL,FUG,GONGSX,etal.Analysisofasurfaceplasmonicwaveguideusingparallelfinitedifferencetimedomainmethod[J].Chinesejournalofradioscience, 2015, 30(4)：668-672.(inChinese).

[3]JIX,LUT,CAIW,etal.DiscontinuousGalerkintimedomain(DGTD)methodsforthestudyof2-Dwaveguide-coupledmicroringresonators[J].Journaloflightwavetechnology, 2005, 23(11)：3864-3874.

[4]ALVAREZJ.Adiscontinuousgalerkinfiniteelementmethodforthetime-domainsolutionofmaxwellequations[D].Granada：UniversityofGranada, 2013：31-39.

[5]PIPERNOS.Symplecticlocaltime-steppinginnon-dissipativeDGTDmethodsappliedtowavepropagationproblems[J].ESAIM：mathematicalmodellingandnumericalanalysis, 2006, 40(5)：815-841.

[6]SHUCW.AbriefsurveyondiscontinuousGalerkinmethodsincomputationalfluiddynamics[J].Advancesinmechanics, 2013, 43：541-554.

[7]SHANKARV,MOHAMMADIANAH,HALLWF.Atime-domain,finite-volumetreatmentfortheMaxwellequations[J].Electromagnetics, 1990, 10(1/2)：127-145.

[8]JINJM.Thefiniteelementmethodinelectromagnetic[M].NewYork：JohnWiley&Sons, 2002.

[9]葛德彪, 魏兵.电磁波时域计算方法[M].西安：西安电子科技大学出版社, 2014:188-191.

李林茜 (1985-),男,新疆人，博士研究生,主要研究方向为计算电磁学.

魏兵 (1970-),男,甘肃人，教授,博士生导师,主要研究方向为电磁理论、复杂系统中的场与波和计算电磁学等.

杨谦 (1989-),男,陕西人，博士研究生,主要研究方向为计算电磁学.

Study on numerical flux of node DGTD method：TM case

LI Linqian1,2WEI Bing1,2YANG Qian1,2GE Debiao1,2WANG Fei1,2

(1.SchoolofPhysicsandOptoelectronicEngineering,XidianUniversity,Xi’an710071,China;2.CollaborativeInnovationCenterofInformationSensingandUnderstanding,XidianUniversity,Xi’an710071,China)

The main difference between the discontinuous Galerkin time domain (DGTD)and the finite element time domain (FETD) is the exchanging field by numerical flux.Based on the weak form solution of TM case in 2D, the physical meaning of numerical flux and the different express between main unit and adjacent unit are firstly described.And then, combining the above, the DGTD iterative formulae are obtained.Finally, numerical examples of line source radiation and interference are given to demonstrate the validity of DGTD algorithm.

discontinuous Galerkin method;numerical flux;nodal basic function

李林茜, 魏兵, 杨谦,等.二维TM波时域非连续伽略金算法理论数值通量研究[J].电波科学学报,2016,31(5)：877-882.

10.13443/j.cjors.2015111702

LI L Q, WEI B, YANG Q, et al.Study on numerical flux of node DGTD method：TM case [J].Chinese journal of radio science,2016,31(5)：877-882.(in Chinese).DOI:10.13443/j.cjors.2015111702

2015-11-17

国家自然科学基金(61231003；61401344；61571348)

O441.4

A

1005-0388(2016)05-0877-06

联系人：李林茜 E-mail：395106835@qq.com