带摄动力拟合的低轨卫星实时定轨STCKF算法
李兆铭 杨文革 丁丹 王超
(1.装备学院研究生院,北京 101416;2.装备学院光电装备系,北京 101416;3.西安卫星测控中心,西安 710043)
带摄动力拟合的低轨卫星实时定轨STCKF算法
李兆铭1杨文革2丁丹2王超3
(1.装备学院研究生院,北京 101416;2.装备学院光电装备系,北京 101416;3.西安卫星测控中心,西安 710043)
针对低轨卫星实时定轨过程中滤波初值及轨道模型不精确导致定轨精度降低的问题,提出一种带摄动力拟合的强跟踪容积卡尔曼滤波(Strong Tracking Cubature Kalman Filter,STCKF)算法.通过强跟踪滤波(Strong Tracking Filter,STF)的等价表示计算次优渐消因子以在线实时调整增益矩阵,强迫残差序列相互正交,有效降低了对初始状态的敏感性.使用欧拉预测校正法对带J2项摄动的轨道动力学方程进行离散,用多项式拟合函数表示其余摄动力以提高模型精度.仿真结果表明,带摄动力拟合的STCKF算法可以有效提高实时定轨精度,并且降低了定轨精度对滤波初值的依赖.
摄动力;多项式拟合;实时定轨;强跟踪容积卡尔曼滤波;欧拉预测校正法
DOI 10.13443/j.cjors.2016011702
引 言
近年来低轨卫星的数量日益增多,轨道资源愈发紧张,为了提高空间资源利用效率,需要对低轨卫星进行监视、编目和预报.对低轨卫星的监视需要实时确定被测卫星的轨道状态,雷达以其全天时、全天候的工作特点成为空间监视系统中一类重要的传感器[1-2],研究利用其输出的测距、测速和测角数据对低轨卫星进行实时定轨在本质上是一个非线性滤波问题,具有重要的研究价值.
扩展卡尔曼滤波[3](Extended Kalman Filter,EKF)算法和无迹卡尔曼滤波[4-5](Unscented Kalman Filter,UKF)算法是解决非线性滤波问题的常用方法.但EKF算法对强非线性系统的滤波精度较低且鲁棒性不强.强跟踪滤波[6-7](Strong Tracking Filter,STF)算法通过在EKF算法中引入次优渐消因子在线实时调整增益矩阵,迫使残差序列相互正交,具有较强的鲁棒性和对初始状态的低敏感性,但并没有在本质上提高滤波精度.UKF算法采用Sigma点的分布近似表示非线性函数的分布,具有较高的滤波精度,但在采样点和权值等参数的选取上没有明确的理论依据,且当变量维数大于3时,负权值的存在使得协方差矩阵不满足半正定条件,降低了滤波稳定性.2009年Arasaratnam[8-9]等采用一组等权值的容积点集来解决贝叶斯滤波积分问题,提出容积卡尔曼滤波(Cubature Kalman Filter,CKF)算法,该算法在本质上与UKF同属一个滤波处理框架,并具有严格的数学证明,同时降低了计算量,目前已经在许多领域取得了应用.针对地基实时定轨中的非线性滤波问题,文献[10]验证了CKF算法在实时定轨中具有更高的精度和数值稳定性.文献[11]采用非线性预测滤波对模型误差进行补偿修正,进一步提高了实时定轨的精度.但在上述研究中状态方程仅考虑了J2项摄动,对于低轨卫星,忽略大气阻力等摄动影响会造成较大的模型误差.同时,实时定轨滤波初值由地面测控中心提供,并外推至滤波初始时刻,当轨道历元与滤波初始时刻间隔较长时,容易造成滤波初值与真实值偏差较大,从而降低实时定轨的精度.
针对低轨卫星实时定轨过程中滤波初值及轨道模型不精确导致定轨精度降低的问题,本文提出一种带摄动力拟合的STCKF算法.该算法兼具了CKF算法的高精度和STF算法的强鲁棒性,有效降低了对初始状态的敏感性.并用多项式拟合函数表示其余摄动力,提高了轨道模型精度.仿真结果表明,本文提出的算法可以在有效提高定轨精度的同时降低定轨精度对滤波初值的依赖,具有一定的工程应用价值.
1 STCKF滤波算法
考虑如下离散非线性动态系统:
xk=f(xk-1)+wk-1;
(1)
yk=h(xk)+vk.
(2)
式中:xk∈Rnx为状态向量;yk∈Rny为量测向量;系统噪声wk-1和量测噪声vk相互独立,且满足wk-1~(0,Qk-1),vk~(0,Rk).
1.1 STF基本算法
STF算法由EKF算法改进而来,其计算过程为:
(3)
(4)
(5)
(6)
(7)
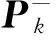
步骤1 估算残差εk的协方差矩阵Vk
(8)
式中,0<ρ≤1被称作遗忘因子,常取ρ=0.95.
步骤2 计算矩阵Nk和Mk
(9)
(10)
为了使状态估计更加平滑,避免渐消因子引起过调节作用,在式(9)中引入弱化因子β(β≥1),其数值主要通过计算机仿真确定.
步骤3 计算渐消因子λk的次优解
(11)
1.2 STF算法的等价表示
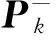
(12)
(13)
(14)
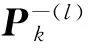
(15)
将式(15)代入式(9)、(10)便得Nk和Mk的等价表达式为:
(16)
(17)
1.3 STCKF算法
CKF算法采用Spherical-Radial原则,利用一组等权值的容积点实现对贝叶斯滤波积分的非线性逼近.当采用三阶容积准则时,容积点总数是状态维数的2倍,容积点及其权值取为
i=1,2,…,m=2nx.
(18)
式中:ξ(i)为容积点;ωi为对应的权值;[1]i表示矩阵
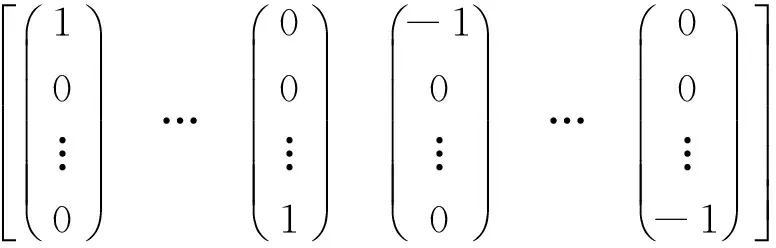
(19)
的第i列.
利用式(16)和式(17)便可以将STF算法与CKF算法结合得到STCKF算法,其步骤如下:
步骤1 滤波器初始化
(20)
循环k=1,2,…,完成以下步骤.
步骤2 时间更新
(21)
(22)
(23)
(24)
步骤3 计算渐消因子λk
(25)
(26)
(28)
(29)
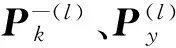
步骤4 量测更新
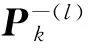
(30)
(31)
(32)
(33)
(34)
(35)
(36)
步骤5 状态更新
(37)
(38)
(39)
2 实时定轨数学模型
2.1 系统状态方程
在低轨卫星所受的摄动力中,J2项摄动是指地球非球形摄动中的J2项部分,是摄动力中的最主要部分.在地球固连坐标系(下文简称地固系)中描述卫星的运动,考虑J2项引力摄动,卫星轨道动力学方程为[12]
(40)
(41)
式中,h为步长.按照上述格式可以将式(40)写成如下状态方程形式:
Xk=f(Xk-1)+wk-1.
(42)
对于低轨卫星,忽略大气阻力等摄动影响会造成较大的模型误差,然而传统的高精度轨道数值计算会造成较大的计算压力,降低实时性.为此,考虑使用多项式拟合函数来近似表达其余摄动力以提高状态模型的精度.
px=a0+a1t+…+amtm.
(43)
由曲线拟合的定义,应使
(44)
取极小值进而可得出系数ai是下面线性方程组的解:
(45)
式中,
(46)
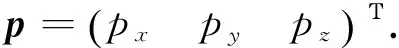
(47)
2.2 量测方程
在雷达站地平坐标系(下文称地平系)中描述量测方程,地固系到地平系的转换矩阵为
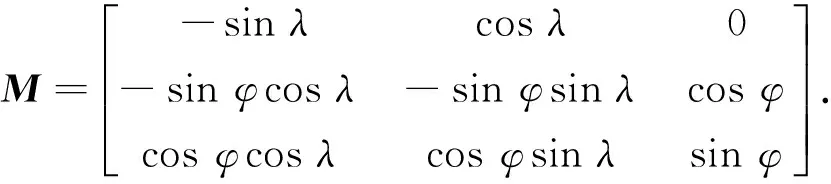
(48)
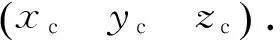
(49)
(50)
(51)
3 仿真实验与分析
STK(Satellite Tool Kit)是美国AGI公司开发的用于航天领域仿真的专业软件,具有很强的适用性和极高的可信度.为了得到可靠的仿真数据,参考轨道数据由STK中高精度轨道预报(High Precision Orbit Propagation,HPOP)算法产生,该算法考虑了地球非球形摄动、大气阻力摄动、三体引力摄动和太阳光压摄动的影响.卫星过境分析用Access模块生成,同时可以生成模拟测距、测速和测角数据.仿真场景为地面雷达站对低轨太阳同步轨道卫星进行实时定轨,轨道历元为1 Jul 2015 13:05:00(UTCG),半长轴6 778.137 km,偏心率0,轨道倾角97.035°,升交点赤经279.066°,近地点幅角0°,真近点角0°.雷达站地理纬度为29.782 6°,经度为108.261°.雷达站对低轨卫星的可见时间窗口为1 Jul 2015 16:14:00(UTCG)到1 Jul 2015 16:21:00(UTCG),持续420 s.假设测距精度为60 m,测速精度为0.1 m/s,测角精度为0.015°.
首先,对摄动力进行拟合,分别用高精度轨道预报算法和状态方程(42)预报可见时间窗口内的轨道值,然后采用6阶多项式对该时间窗口内的摄动力进行拟合,拟合结果为

采用6阶多项式拟合是仿真得出的结论,而低阶多项式拟合的精度较低.用整个过境段的高精度轨道预报与状态方程预报的差拟合出摄动力,从而修正状态方程进行滤波迭代.低轨卫星过境时间为5 min左右,每次定轨都要对摄动力进行重新拟合.以对高精度轨道拟合为例,给出x、y、z三个方向的拟合误差,如图1所示.可以看到,由于卫星过境时间较短,可见弧段轨道曲率较小,因此用多项式拟合可以达到较高的拟合精度.
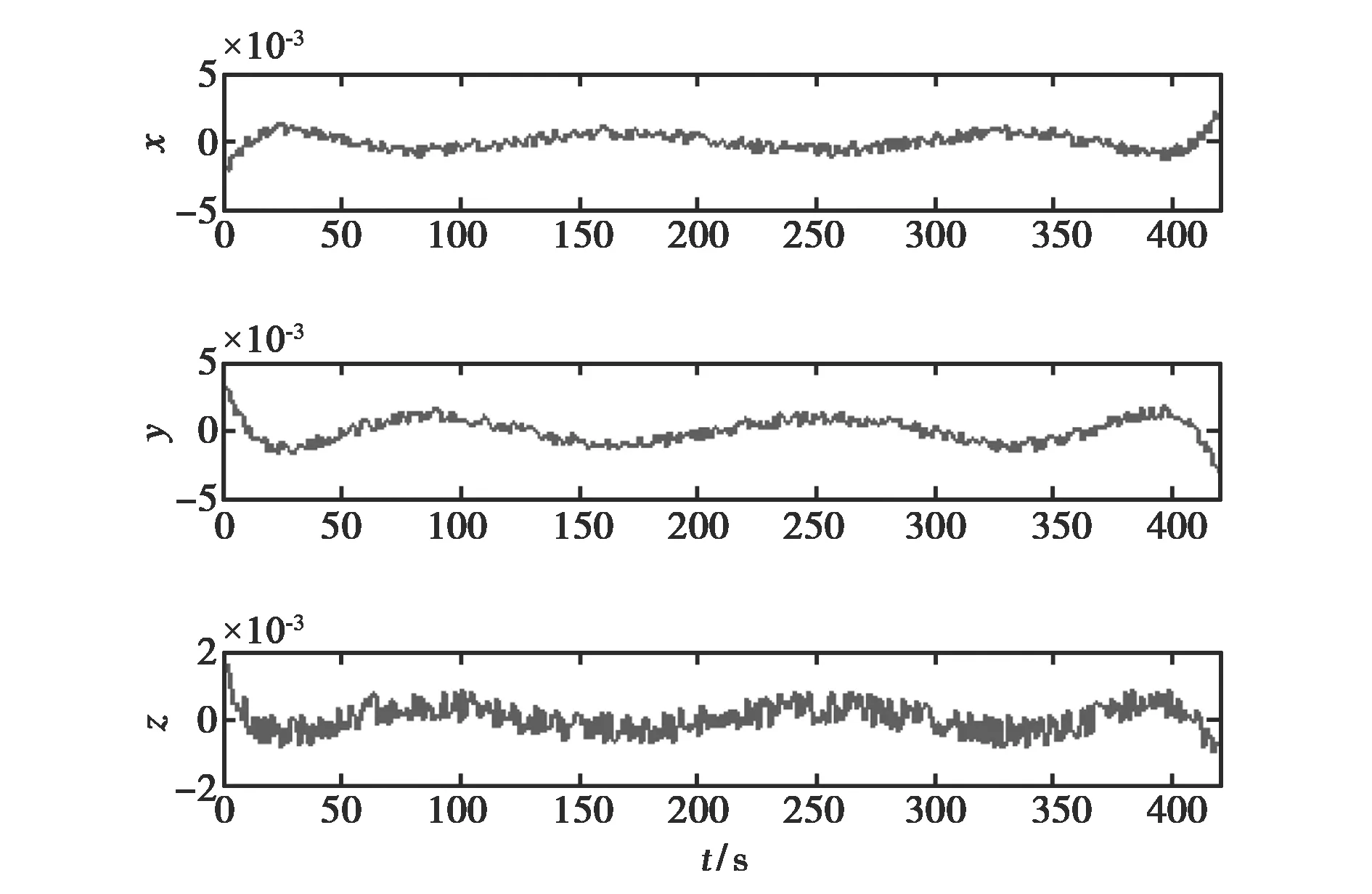
图1 x、y、z三个方向的拟合误差
为了验证本文提出的带摄动力拟合STCKF算法的性能,将其与标准CKF、带摄动力拟合CKF和STCKF算法分三种情况进行仿真对比分析,如表1所示.

表1 三种仿真情况
三种情况的滤波初值分别为:
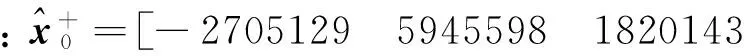
2177 -1252 7324];
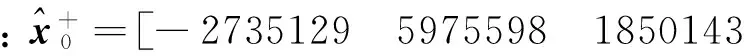
2177 -1252 7324];
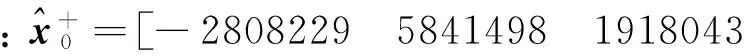
2177 -1252 7324].
STCKF滤波器参数为:
β=100,ρ=0.95.
采用位置均方根误差(Root Mean Square Error,RMSE)和速度RMSE来评价实时定轨结果,位置RMSE定义如下:
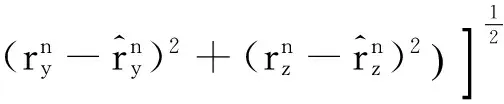
(52)
式中,N为蒙特卡洛仿真次数.
取观测数据时间间隔T=1.0 s,运行200次蒙特卡洛仿真.三种情况的仿真结果如图2~4所示,为了表述得更加清晰,对300~420 s进行局部放大,并统计位置和速度的平均RMSE列于表2.从仿真结果可以看出,当滤波初值与真实值相差较小时,CKF算法与STCKF算法精度相当,带摄动力拟合CKF算法与带摄动力拟合STCKF算法精度相当,说明强跟踪算法本身并没有提高精度,而是用拟合摄动力修正了模型,从而将定轨位置精度提高了32.728 m.随着滤波初值与真实值的偏差逐渐增大,CKF算法与带摄动力拟合CKF算法的定轨精度明显下降,而STCKF算法与带摄动力拟合STCKF算法的定轨精度基本维持不变,证明了强跟踪算法对滤波初值的低敏感性.当滤波初值与真实值的偏差达到173 km时,STCKF算法定轨精度维持在58 m左右,而带摄动力拟合的STCKF算法的定轨精度维持在28 m左右.同时,带摄动力拟合STCKF算法运行200次的时间为60.3 s,平均运行一次的时间为0.301 5 s,而运行一次需要迭代计算420 s的数据,由此可见该算法具有很强的实时性.
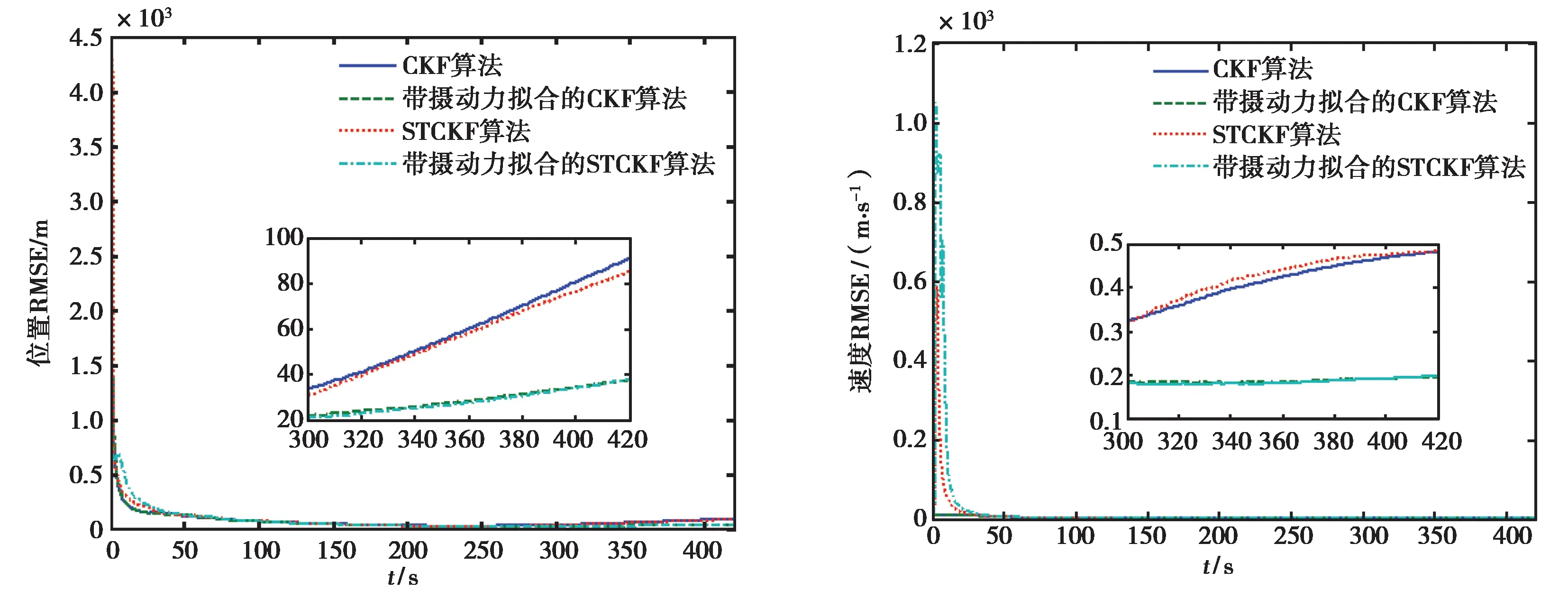
(a) 位置RMSE比较 (b) 速度RMSE比较图2 四种算法对比(情况一)
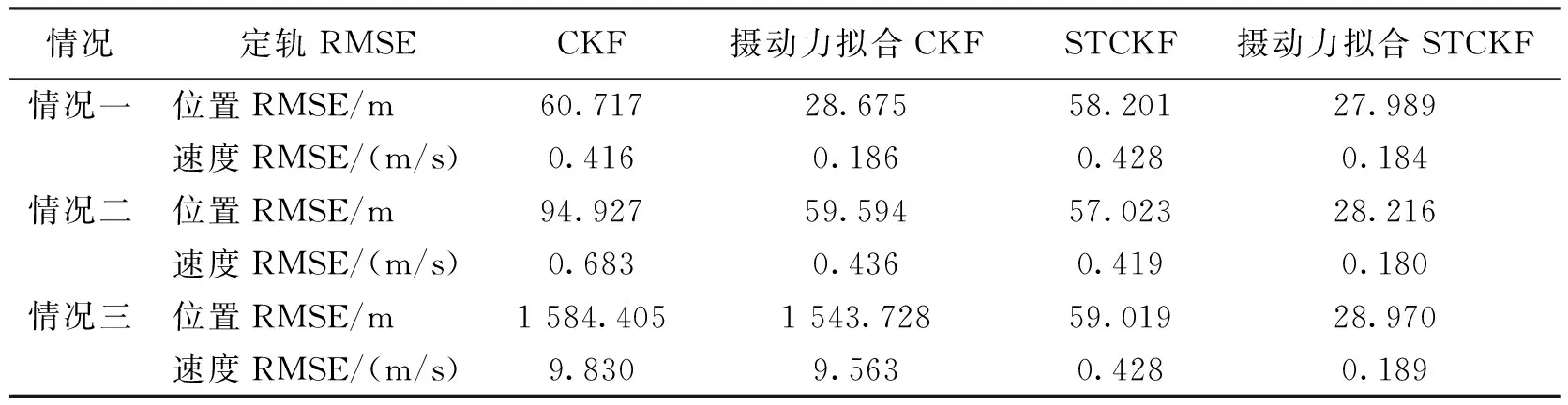
情况定轨RMSECKF摄动力拟合CKFSTCKF摄动力拟合STCKF情况一位置RMSE/m60.71728.67558.20127.989速度RMSE/(m/s)0.4160.1860.4280.184情况二位置RMSE/m94.92759.59457.02328.216速度RMSE/(m/s)0.6830.4360.4190.180情况三位置RMSE/m1584.4051543.72859.01928.970速度RMSE/(m/s)9.8309.5630.4280.189
4 结 论
针对低轨卫星实时定轨过程中滤波初值及轨道模型不精确导致定轨精度降低的问题,提出了一种带摄动力拟合的STCKF算法.通过STF的等价表示计算次优渐消因子以在线实时调整增益矩阵,强迫残差序列相互正交,有效降低了对初始状态的敏感性.使用欧拉预测校正法对带J2项摄动的轨道动力学方程进行离散,用多项式拟合函数表示其余摄动力以提高模型精度.仿真结果表明:
1) 当滤波初值与真实值相差较小时,在轨道模型中加入摄动力的多项式拟合函数可以有效提高滤波定轨精度.
2) 随着滤波初值与真实值的偏差逐渐增大,CKF算法的定轨精度明显下降,而本文算法则将定轨精度维持在28 m左右,证明本文算法对滤波初值具有低敏感性.
[1]金旺, 吴振森, 吴健, 等.非相干散射雷达探测空间碎片实验研究[J].电波科学学报, 2011, 26(5):956- 960.
JIN W, WU Z S, WU J, et al.Space debris experimentation study using incoherent scatter radar[J].Chinese journal of radio science, 2011, 26(5):956- 960.(in Chinese)
[2]金旺, 吴振森, 吴健, 等.930MHz雷达测空间碎片散射截面[J].电波科学学报, 2012, 27(6):1076-1080.
JIN W, WU Z S, WU J, et al.Space debris cross section observations with 930MHz radar[J].Chinese journal of radio science, 2012, 27(6):1076- 1080.(in Chinese)
[3]PSIAKI M L.Backward-smoothing extended kalman filter[J].Journal of guidance control and dynamics, 2005, 28(5):885-894.
[4]JULIER S, UHLMANN J, DURRANT-WHYTE H F.A new method for nonlinear transformation of means and covariances in filters and estimators[J].IEEE transactions on automatic control, 2000, 45(3):477-482.
[5]JULIER S J.The scaled unscented transformation[C]// Proceedings of the American Control Conference.May 8-10, 2002:4555-4559.
[6]ZHANG Z T, ZHANG J S.A strong tracking nonlinear robust filter for eye tracking[J].Journal of control theory and applications, 2010, 8(4):503-508.
[7]钱华明, 黄蔚, 孙龙, 等.基于多重次渐消因子的强跟踪UKF姿态估计[J].系统工程与电子技术, 2013, 35(3):581-583.
QIAN H M, HUANG W, SUN L, et al.Attitude estimation of strong tracking UKF based on multiple fading factors[J].Systems engineering and electronics, 2013, 35(3):581-583.(in Chinese)
[8]ARASARATNAM I, HAYKIN S.Cubature Kalman filters[J].IEEE transactions on automatic control, 2009, 54(6):1254-1269.
[9]ARASARATNAM I, HAYKIN S.Cubature Kalman smoothers[J].Automatica, 2010, 47(10):2245- 2250.
[10]宁夏, 叶春茂, 杨健, 等.容积卡尔曼滤波在空间目标轨道确定中的应用[J].电波科学学报, 2014, 29(1):27-32.
NING X, YE C M, YANG J, et al.Cubature Kalman filtering for orbit determination of space targets[J].Chinese journal of radio science, 2014, 29(1):27-32.(in Chinese)
[11]李志军, 侯黎强.一种用于实时轨道确定的NPF-SRCKF滤波算法[J].宇航学报, 2014, 35(7):812-816.
LI Z J, HOU L Q.An improved NPF-SRCKF based algorithm for spacecraft orbit determination[J].Journal of astronautics, 2014, 35(7):812-816.(in Chinese)
[12]王向磊, 丁硕, 苏牡丹.UKF在基于地磁场的自主导航中的应用[J].测绘科学, 2011, 36(6):103-105.
WANG X L, DING S, SU M D.Application of UKF in geomagnetic field based autonomous navigation[J].Science of surveying and mapping, 2011, 36(6):103-105.(in Chinese)
[13]张池平.计算方法[M].北京:科学出版社, 2006.
ZHANG C P.Computing method[M].Beijing:China Science Publishing &Media Group Ltd, 2006.(in Chinese)

李兆铭 (1989-),男,黑龙江人,装备学院博士研究生,研究方向为航天测控最优状态估计.
An STCKF algorithm for LEO satellite orbit determination with disturbing fitting function
LI Zhaoming1YANG Wenge2DING Dan2WANG Chao3
(1.CompanyofPostgraduateManagement,AcademyofEquipment,Beijing101416,China;2.DepartmentofOpticalandElectricalEquipment,AcademyofEquipment,Beijing101416,China;3.Xi’anSatelliteControlCenter,Xi’an710043,China)
A strong tracking cubature Kalman filter(STCKF) algorithm with disturbing fitting function is proposed for Leo satellite orbit determination when inaccurate initial value and orbit model lead to low precision of filter.The suboptimal fading factor is calculated using the equivalent expression of strong tracking filter(STF) to adjust the gain matrix online and to force the residual sequence orthogonal to each other, which effectively reduces the sensitivity to the initial state.Improved Eular method is used to disperse the orbital dynamic equation withJ2perturbation, and the polynomial fitting function is used to represent the rest disturbing force.The simulation results show that STCKF with disturbing fitting function can effectively improve the orbit determination accuracy, and reduce the dependence on initial value of the filter.
disturbing force;polynomial fitting;orbit determination;strong tracking cubature Kalman filter;improved Eular method
李兆铭, 杨文革, 丁丹, 等.带摄动力拟合的低轨卫星实时定轨STCKF算法[J].电波科学学报,2016,31(5):843-850.
10.13443/j.cjors.2016011702
LI Z M, YANG W G, DING D, et al.An STCKF algorithm for LEO satellite orbit determination with disturbing fitting function[J].Chinese journal of radio science,2016,31(5):843-850.(in Chinese).DOI:10.13443/j.cjors.2016011702
2016-01-17
国家高技术研究发展计划(2015AA7026085)
V249.3
A
1005-0388(2016)05-0843-08
联系人:李兆铭 E-mail:ilovemolly@163.com

