GPS精密星历轨道内插与拟合方法研究
何丽娜 张成
(河海大学地球科学与工程学院,江苏南京 211100)
GPS精密星历轨道内插与拟合方法研究
何丽娜 张成
(河海大学地球科学与工程学院,江苏南京 211100)
GPS精密星历以15min为间隔发布卫星精密轨道。在实际应用中,往往需要求解任意时刻卫星精密轨道。常用的方法有拉格朗日插值法和切比雪夫多项式拟合法。基于此,利用2007年7月8日的2号卫星精密星历数据,编程实现了不同阶数条件下的轨道拟合,并比较2种方法的精度,分析各自的优缺点。
精密星历;拉格朗日插值法;切比雪夫多项式拟合法;卫星坐标
一般有2种方法可以得到GPS卫星轨道,一是由广播星历计算获取,参考历元下轨道精度在2m左右,难以达到高精度应用要求;另一种是通过精密星历内插或拟合得到,精度较高[1]。由于IGS精密星历及精密钟差是采样间隔为15min的离散数据,为了得到连续的星历及钟差参数,在应用前对精密星历进行插值或拟合,以得到卫星连续轨道。本文介绍求解卫星连续轨道的2种常见方法,分别是拉格朗日多项式插值法和切比雪夫多项式拟合法,通过实例计算分析2种方法各自的特点。
12 种方法求解连续卫星轨道的原理
1.1 拉格朗日多项式插值卫星坐标的原理
设在n+1个时间为t1,t2,……,tn+1插值节点上的卫星坐标分别为x1(t1),x2(t2),……,xn+1(tn+1),那么在任意时刻t卫星的坐标可表示为:

利用式(1)在X、Y、Z方向上分别进行插值处理,即可得到任意时刻的卫星坐标。插值的阶数为节点数减1[2]。
1.2 切比雪夫多项式拟合卫星坐标的原理
在时间段[t0,t0+Δt]内,将GPS星历用n阶切比雪夫多项式拟合,t0为初始历元,Δt为拟合时间区间长度,由下面的转换公式把t∈[t0,t0+Δt]转换为τ∈[-1,1]。

则卫星坐标X、Y、Z分量用如下切比雪夫多项式表示:

式(3)中,n为切比雪夫多项式阶数,Cxi、Cyi、Czi分别是X、Y、Z坐标分量的切比雪夫多项式系数。切比雪夫多项式Ti用以下递推公式确定。

用最小二乘方法求解多项式系数原理如下:

式(5)中,

由最小二乘原理VTPV=min得误差方程的解为:
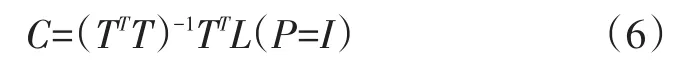
式(6)中,C即为切比雪夫多项式系数,这时带入式(2)和(4)中,即可利用式(3)计算得到卫星求解时刻的轨道坐标[3]。X、Y、Z分别平差计算出一套多项式系数,即经过3次这样的过程可以得到卫星任意时刻的精密坐标。
22 种方法求解连续卫星坐标的比较
IGS精密星历给出的是间隔15min的卫星轨道,如果要获得任意时刻的卫星坐标,需要经过插值或拟合方法。如果插值或拟合的阶数较低,则得到的坐标精度较低,不能满足实际需要,但是由于精密星历本身的精度限制以及高阶多项式本身的数学问题,阶数并不是越高越好,因此选择合适的阶数是获得精确坐标的前提。
本文分别用上述2种方法分别编程对2007年7月8日的2号卫星0∶00-6∶00共25个时刻数据进行计算并比较如下。
2.1 拉格朗日插值法
以2号卫星10 800s时刻作为插值点,因此去除该时刻数据使其不作为插值节点,利用该时刻前后分别2个时刻的数据(即4阶拉格朗日插值)至6个时刻数据(即12阶拉格朗日插值),分别插值计算,得到的10 800s时刻的坐标结果如表1所示。
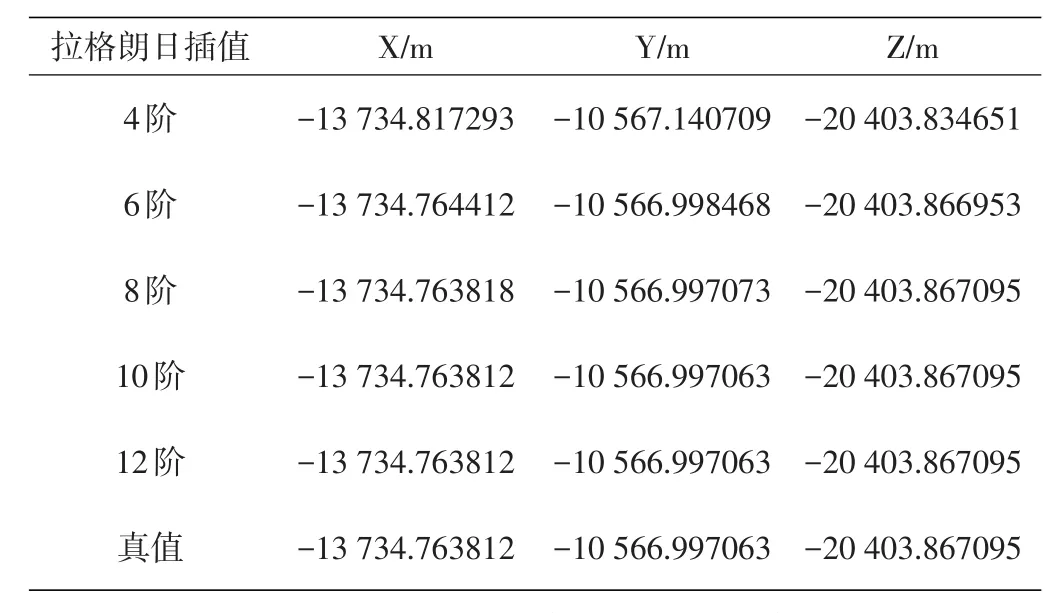
表1 各阶拉格朗日插值得到的10 800s的2号卫星的坐标值
由表1数据可以看出,当拉格朗日插值阶数达到8阶时,精度可达到厘米级;阶数小于8时,阶数增加对精度提高有明显作用;大于8时,阶数越高,精度没有显著提高。所以,一般使用8阶拉格朗日内插卫星坐标。
2.2 切比雪夫多项式拟合法
将10 800s时刻作为拟合点,去除2号卫星在该时刻的卫星坐标,利用选取的6h共24个时刻的数据分别进行拟合计算,得到卫星精密坐标拟合结果如表2所示。

表2 各阶切比雪夫多项式拟合10 800s的2号卫星的坐标值
由表2数据可以看出,当切比雪夫多项式插值阶数达到10阶时,精度可达到厘米级;阶数小于10时,阶数增加对精度提高有明显作用;大于16时,阶数越高,精度没有显著提高。所以,一般使用12~15阶切比雪夫多项式拟合卫星坐标。
3 结语
通过比较拉格朗日插值计算卫星坐标和切比雪夫多项式拟合卫星坐标,得出以下结论:①选择合适阶数的插值和拟合方法均可得到给定时刻下的卫星坐标值;②8~10阶拉格朗日内插的卫星坐标达到厘米级精度,超过10阶精度提高不明显,一般使用8~10阶拉格朗日插值进行卫星坐标的计算,该方法计算简单,容易实现,但由于阶数改变即选择的节点不同,方程要重新建立,使计算量增大;③12~15阶切比雪夫拟合卫星坐标可达到厘米级精度,超过15阶精度提高不明显,一般使用12~15阶切比雪夫拟合卫星坐标,该方法精度较好,是工程中使用的经典方法之一,但由于要平差求解切比雪夫多项式系数,程序较复杂,涉及求逆问题,计算上不太方便。
[1]叶达忠.GPS精密单点定位(PPP)原理、测试及应用[J].广西水利水电,2007(1):24-26.
[2]魏二虎,柴华.GPS精密星历插值方法的比较研究[J].全球定位系统,2006(5):13-15.
[3]陈正阳,易重海.用切比雪夫多项式进行GPS卫星轨道标准化[J].矿山测量,2002(2):5-7.
Study on Orbit Interpolation and Fitting Method of GPS Precise Ephemeris
He LinaZhang Cheng
(School of Earth Science and Engineering,Hohai University,Nanjing Jiangsu 211100)
GPSprecise ephemeris with 15min interval released satellite precise orbit.In practical applications,it is often required tosolvethesatellitepreciseorbit at any time.Thecommonly used method hasLagrangeinterpolation method and Chebyshev polynomial fitting.Based on this,by July 8,2007 2 satelliteephemerisdata,thetrack fitting of different order condition was realized by programming,and the accuracy of the two methods were compared,and the advantage sand disad vantages of each method were anal yzed.
precise ephemeris;lagrang interpolating method;chybishev polynomial fitting;satellite coordinate
P228.4
A
1003-5168(2016)11-0031-02
2016-10-19
何丽娜(1985-),女,博士,讲师,研究方向:大地测量。

