一类具有Logistic增长的SIQS传染病模型
程晓云,胡志兴
(1.西安培华学院 通识教育中心,西安 710065; 2.西北大学 数学学院,西安 710069;3.北京科技大学 数理学院,北京 100083)
一类具有Logistic增长的SIQS传染病模型
程晓云1,2,胡志兴3
(1.西安培华学院 通识教育中心,西安 710065; 2.西北大学 数学学院,西安 710069;3.北京科技大学 数理学院,北京 100083)
建立了一类具有Logistic增长的SIQS传染病模型,利用Hurwitz判据、Lasalle不变原理及Dulac判别法等,证明了疾病消除平衡点的全局稳定性和地方病平衡点的局部稳定性,及在无因病死亡时地方病平衡点的全局稳定性.而且对所得结果进行了数值模拟.
传染病模型;平衡点;局部渐近稳定;全局渐近稳定
传染病动力学是研究传染病的一种重要方法,它是根据种群成长的特性,疾病的发生及在种群内的传播规律,建立反映传染病动力学特征的数学模型.通过对模型动力学状态的定性、定量分析及数值模拟,预测疾病的发展趋势,并寻求疾病流行原因和关键因素,从而为传染病的预防和控制提供一定的指导.众所周知,在传染病的控制中,对染病者隔离是重要的措施,因此考虑具有隔离项的传染病模型具有重要的现实意义.
1 模型的建立
文献[1-5]研究了对染病者进行隔离的传染病模型,文献[6-9]研究了具有Logistic增长的传染病及生态模型.本文将研究染病种群隔离且隔离恢复后不具免疫力的具有Logistic增长的SIQS传染病模型.疾病的传播机制如下:

图1 疾病的传播机制图
由图1建立相应的传染病模型:
(1)
该模型参数除α为非负数外,其余均为正.其中S、I、Q分别表示t时刻易感种群、染病种群及隔离种群的数量,β、γ分别表示疾病的传染率和恢复率,δ表示对染病种群的隔离率,α表示染病种群和被隔离种群的因病死亡率,ε表示隔离种群的恢复率.种群数量N=S+I+Q满足方程:

(2)
当种群无疾病传播时,种群的增长符合Logistic方程:

其中η=b-d表示种群的内禀增长率,b和d分别表示种群的自然出生率和自然死亡率,且假设因病死亡率比自然死亡率要小,即α 作归一化变换:x=S/N,y=I/N,z=Q/N,则x+y+z=1.于是模型(1)和(2)等价于模型(3): (3) 系统(3)在xyN空间的正向不变集: (4) 定理1 系统(3)在区域D内总存在平衡点E1(0,0,K);当R0>1,φ<1时,存在正平衡点E2(y2,z2,N2).其中 定理2 当R0≤1时,疾病消除平衡点E1在区域D内全局渐近稳定. 证明 通过求系统(3)在E1处的Jacobian矩阵,容易证得当R0<1时,E1局部稳定. 下面分两种情形证E1在区域D内全局渐近稳定: 1)若β>α作Liapunov函数V=y,由R0<1得β<(γ+δ+α+b)-η. 则 V=y[β-(γ+δ+α+b-η)-η(1-N/K)-(β-α)(y+z)]≤0 及最大不变集M=E={V′=0}={y=0}.由LaSalle不变原理及极限系统理论知识即证:只要初值N0>0,系统(3)从D内出发的任一解都趋向于平衡点E1(0,0,K). 2)若β≤α构造Liapunov函数V=y+z,V沿系统(3)的全导数: V′=y(β-α)[1-(y+z)]-γy-(ε+α)z-(y+z)[b(1-N/K)+dN/K+αz]≤0 及最大不变子集M=E={V′=0}={y=0,z=0}. 定理3 当R0>1且φ<1时,地方病平衡点E2局部渐近稳定. 证明 系统(3)在E2处的Jacobian矩阵的特征方程: H(λ)=λ3+mλ2+nλ+p=0, (5) 其中m=ηN2/K+(β-α)y2+(ε+α+d-αz2)>0, n=αN2η/K(y2+z2)+(β-α)(ε+δ+α+d)y2+ηN2/K[(β-α)y2+(ε+α+d-αz2)]>0, p=ηN2/Ky2(β-α)(ε+δ+α+d)+αN2ηy2/K(ε+δ+α+d)>0, 则 mn-p=(ε+δ+α+d)y2{(β-α)[(β-α)y2+(ε+α+d-αz2)]-αN2η/K}+ m{αN2η/K(y2+z2)+ηN2/K[(β-α)y2+(ε+α+d-αz2)]}, 令f(β)=(β-α)[(β-α)y2+(ε+α+d-αz2)]-αN2η/K,并将y2,z2,N2代入,可得 f(β)=(ε+α+d)β3+[(ε+α+d)(ε-γ-2α)-αδ]β2+ α(ε+α+d)(2γ+δ+2α+d-ε)β+(ε+δ+α+d)(α2-αη)β+ αδ(γ+δ+2α+d)β-2α2(γ+δ+α+d)(ε+δ+α+d), 及 f‴(β)=6(ε+α+d)>0,故f″(β)>f″(γ+δ+α+d). 又f″(γ+δ+α+d)=(ε+α+d)(4γ+6δ+2α+6d+2ε)-2αδ>0,故f′(β)单调递增,因此f′(β)>f′(γ+δ+α+d).而 f′(γ+δ+α+d)=(ε+α+d)[(γ+δ+α+d)(α+γ+3δ+2ε+3d)-α(ε+δ+d)-αη+α2]- αδ(γ+δ+d)-αηδ+α2δ >(ε+α+d)[(γ+δ+α+d)(α+γ+3δ+2ε+3d)-α(ε+δ+d)]- αδ(γ+δ+d)>0, 所以f(β)单调递增,故f(β)>f(γ+δ+α+d). 又 f(γ+δ+α+d)=(γ+δ+α+d)(ε+δ+α+d)[α(γ+δ+d-η)+(ε+d)(γ+δ+d)], 因为α 当α=0时,系统(1)变为: (6) 定理5 当R0′<1时,系统(6)的无病平衡点E1′(0,0,K)在区域D′内全局渐近稳定. 证明 当R0′<1时,容易证得平衡点E1′局部渐近稳定. 构造Liapunov函数V=I,显然有V′≤0,且最大不变子集M′={V′=0}={I′=0}. 由Lasalle不变原理,点E1′在区域D′内是全局吸引的,结合局部稳定性,命题得证. 对系统(6),由第三个方程可知,当t→时,N→K.故系统(6)的极限系统为: (7) 定理6 对极限系统(7),当R0′>1,惟一的地方病平衡点E2′在区域D″内全局渐近稳定. 证明 当R0′>1时,容易证明E2′局部渐近稳定. 由定理6并结合极限系统的理论知识,可得下面的定理: 定理7 当R0′>1时,系统(6)的惟一正平衡点E2′在区域D″内全局渐近稳定,即当无因病死亡时,系统(3)的正平衡点全局渐近稳定. 图2 β=0.01,α=0.005时系统(3)的轨线图 为验证本文结果,对模型(3)的参数赋值,通过matlab软件进行数值模拟.不妨令:K=1 000,b=0.05,d=0.01,γ=0.03,ε=0.2,δ=0.5. 初值:(0.8,0.08,300),(0.7,0.05,890),(0.46,0.27,680),(0.1,0.75,500). 1)令β=0.01,α=0.005,此时R0<1,系统(3)满足定理2,则系统(3)的轨线的图像如图2. 图2表明,系统(3)的轨线最终趋向于无病平衡点,即染病种群和隔离种群在总种群中的比例最终为零,此时传染病是最终消除. 2)令β=0.8,α=0,此时R0′>1,系统(3)满足定理7,则系统(3)的轨线的图像如图3. 图3 β=0.8,α=0时系统(3)的轨线图 图4 β=0.8,α=0.005时系统(3)的轨线图 图3表明,系统(3)的轨线最终趋于正平衡点,即染病种群和隔离种群在总种群中所占的比例最终趋于某一不变的不为零的常数,此时传染病最终不会消除而成为地方病. 3)令β=0.8,α=0.005,此时R0>1,系统(3)存在惟一正平衡点,则系统(3)的轨线的相图如图4. 图4表明,在存在因病死亡时,系统(3)的正平衡点是稳定的.因此推测定理7可放宽到因病死亡存在的情况,这种情况有待进一步研究. [1] 陈军杰.几个具有隔离的传染病模型的局部稳定性和全局稳定性[J].生物数学学报,2004,19(1):57-64. [2] 李建全,王峰,马知恩.一类带有隔离的传染病模型的全局分析[J].工程数学学报,2005,1(22):20-24. [3] 李琪,陈绍东.一类SIQS传染病模型稳定性分析[J].兰州理工大学学报(自然科学版),2012,38(1):167-172. [4] 杨俊仙,徐丽.一类具有非线性发生率和时滞的传染病模型的全局稳定性[J].山东大学学报(理学版),2014,49(5):67-74. [5] 王雪琴,杨秀香.具有非线性传染率的SIQR流行病模型的全局稳定性分析[J].西北师范大学学报(自然科学版),2012,48(5):18-22. [6] 王辉,,胡志兴,马知恩.非线性接触率和种群动力学对SI传染病模型的影响[J].生物数学学报,1997,5(12):434-438. [7] 苏方林,罗桂烈,江佑霖.一类具有Logistic增长率的SIS传染病模型的概周期解[J].数学研究,1999,32(4):249-354. [8]XIAOYan-ni,CHENLan-sun.Modelingandanalysisofapredator-preymodelwithdiseaseintheprey[J].MathematicalBiosciences,2001,171:59-82. [9] 宫兆刚,蔡江涛,阳志峰.一类具有种群Logistic增长的SIR传染病模型的稳定性[J].贵州师范大学学报(自然科学版),2012,30(1):64-69. [责任编辑 马云彤] A Class of SIQS Epidemic Model with Logistic Growth CHENG Xiao-yun1, 2, HU Zhi-xing3 (1.General Education Center, Xi’an Peihua University, Xi’an 710065, China; 2.School of Mathematics, Northwest University,Xi’an 710069, China; 3. School of Applied Science,Beijing University of Science and Technology, Beijing 100083, China) In this paper, a class of SIQS epidemic model with logistic growth is established, by using of the Hurwitz criterion, the Lasalle invariant principle and the Dulac discriminant method, etc., the global stability of the equilibrium point of disease elimination and the local stability of equilibrium point of endemic diseases are proved. Moreover, the obtained results are numerically simulated. epidemic model; equilibrium point; local asymptotic stability; global asymptotic stability 1008-5564(2016)04-0026-05 2016-04-12 国家自然科学基金资助项目(61174209) 程晓云(1978—),女,山西应县人,西安培华学院通识教育中心讲师,西北大学数学学院博士研究生,主要从事生物数学与逻辑代数研究; 胡志兴(1962—),男,陕西汉中人,北京科技大学数理学院应用数学系教授,博士,硕士生导师,主要从事非线性动力系统与生物数学研究. R51;O175.1 A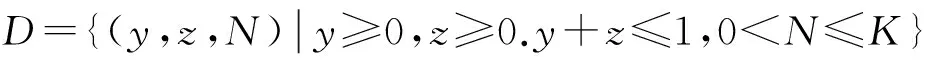
2 平衡点的存在性
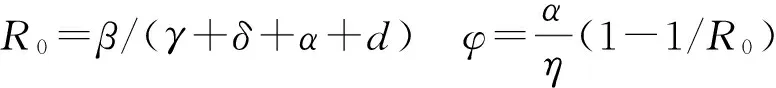
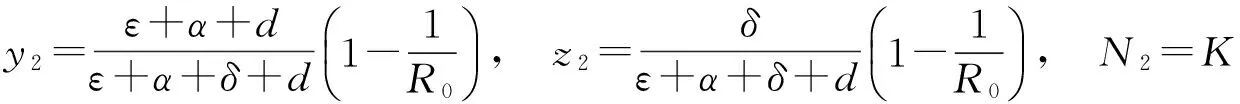
3 疾病消除平衡点的全局稳定性
4 地方病平衡点的局部稳定性
5 无因病死亡时平衡点的全局稳定性
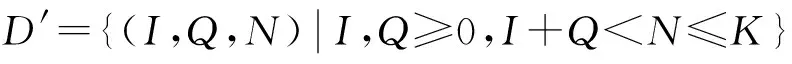
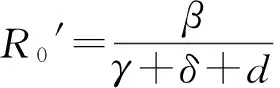
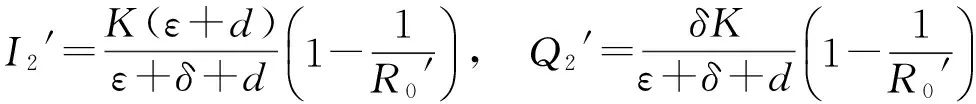

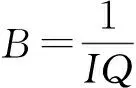
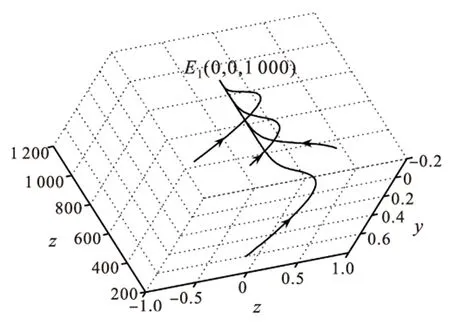
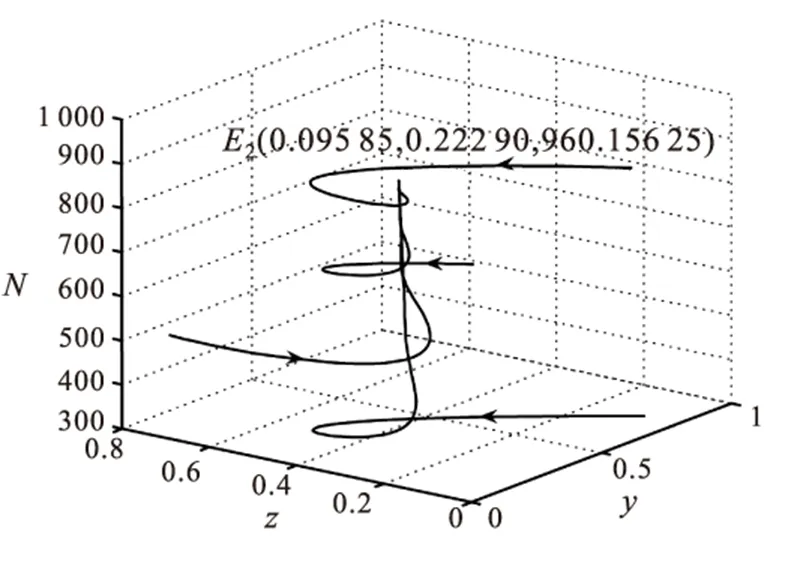
6 数值模拟及结论