多介质球(轴)对称问题的高精度数值模拟方法
刘肖肖
(南京航空航天大学 理学院,南京 211106)
多介质球(轴)对称问题的高精度数值模拟方法
刘肖肖
(南京航空航天大学 理学院,南京 211106)
给出了球对称和轴对称多介质流动问题的高精度数值模拟方法.在界面处利用RGFM(Real Ghost Fluid Method)方法跟踪界面并定义界面边界条件,将多介质流动问题转化为单介质流动问题,并利用高精度RKDG(Runge-Kutta Discontinuous Galerkin)法进行计算.对于水下爆炸等问题中出现的空化现象,采用等熵的单流体空化模型来处理.数值试验结果表明,该方法能够有效捕捉各种物理现象,保持界面清晰,且大大提高计算效率.
多介质;对称;RKDG;RGFM;空化
Cockburn和Shu等构造了求解一维守恒律方程的高阶RKDG方法[1-2],并且将该方法成功地推广到多维标量守恒律[3]和多维守恒律方程组[4].RKDG方法具有高精度和紧性,易于处理复杂的边界,被广泛应用于流体力学问题的数值模拟.
可压缩多介质流动问题是计算流体力学研究的重要内容之一,该类问题的数值模拟在流体力学,航空航天,爆炸等领域应用非常广泛,尤其是涉及到激波与不同介质交互界面的相互作用的空气爆炸,气泡变形与坍塌以及水下爆炸等问题.在水下爆炸等问题中,由于低压区有时会出现空化现象,且空化气泡破裂对船舶,水下舰艇会产生非常大的破坏作用,因此准确的模拟空化问题也具有非常重要的意义.
对于多介质流动问题的数值模拟,由于在界面两边流体的状态方程不同,流体的密度会出现大梯度变化,若采用单介质流动问题的数值方法,数值不稳定情况就会出现,在界面处会出现非物理振荡,甚至使得计算难以进行.Fedkiw等提出的GFM(Ghost Fluid Method)方法[5]是一个简单有效的方法,Liu等在此基础上构造了更加稳健的MGFM(Modified GFM)方法[6].本文利用RGFM[7]来处理界面,通过求解Level Set方程跟踪界面的位置,在界面处利用Riemann问题的解定义界面边界条件,将多介质问题转化为单介质问题,并结合高精度RKDG方法进行求解.
1 方程
1.1 控制方程
球对称欧拉方程组为:
(1)

轴对称欧拉方程组为:
(2)

为了使欧拉方程组封闭,需要加入如下状态方程:
理想气体的状态方程:
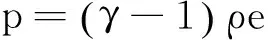
(3)
水的状态方程:
p=(N-1)ρe-NB
(4)
其中γ、N、β均为正常数,将在具体算例中给出.
1.2 空化区域混合流体的状态方程
水中因压力降低会产生的空化现象,对于空化区域的混合流体,状态方程采用Liu等提出的等熵单流体空化模型[8].
混合流体的状态方程:
(5)
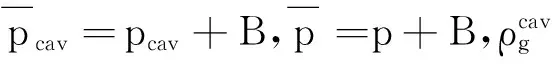
1.3 Level Set方程
本文通过求解Level Set方程跟踪界面的位置,二维Level Set方程为
(6)
其中φ(x,y,t)为符号距离函数,u和v分别为径向和z方向的速度.利用求解Hamilton-Jacobi方程的三阶RKDG方法求解方程(6),可以得到准确的界面位置.
2 数值计算方法
为简单起见,本文只给出一维含源项欧拉方程组(1)的离散方法.
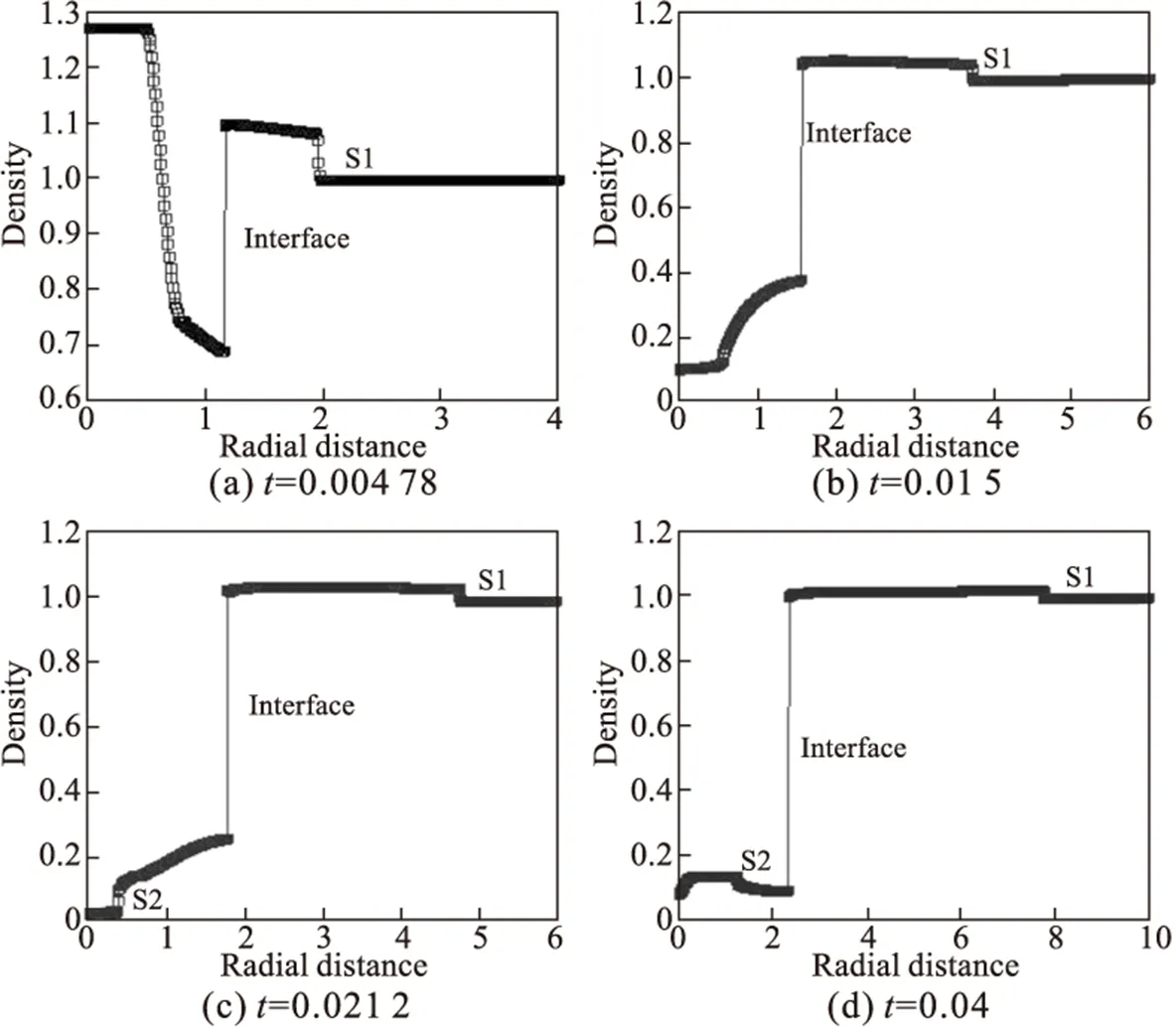
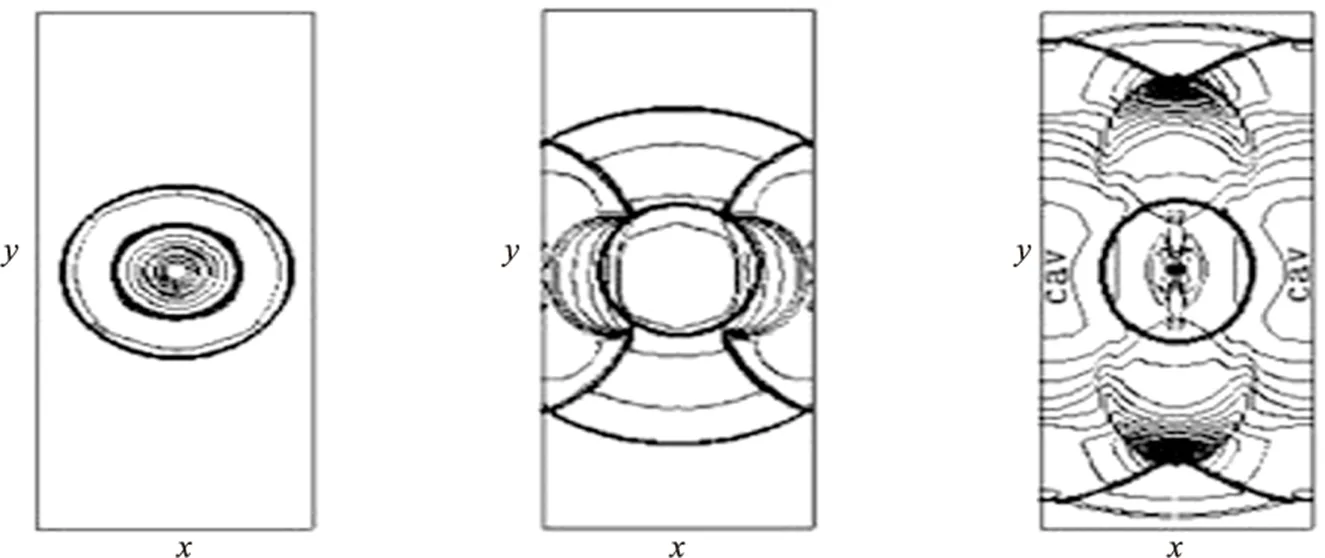
首先将计算区域[a,b]划分成N个网格,a=r1/2 (7) (8) (9) (10) (11) (12) Uh(x,t)在网格Ij左右边界处的值可表示为: (13) (14) 其中TVD限制器函数为: (15) 对于方程组(1),(2),Uh为向量函数,可将Uh映射到特征空间,对其每一个分量重复式(13)~(14)即可. 三维欧拉方程组经坐标变换后得到方程组(1)和(2),可见r=0处为奇点,直接用数值方法求解方程组,会导致数值不稳定.为了保证所采用的数值格式与方程组(1),(2)的相容性,在奇点附近采用如(16)的守恒型方程组 (16a) (16b) 在奇点处u=0 (16c) α=2时为轴对称问题在任意z处奇点附近的流动控制方程,α=3为球对称问题在奇点附近的流动控制方程. 对于方程组(16)采用如下差分格式离散: (17a) (17b) (17c) (17d) 其中λr=Δt/Δr,下标“1”和“2”分别表示变量在r1=Δr和r2=2Δr处的值,“0”表示变量在r=0处的值. 将二阶(k=1)精度RKDG方法中的方程(12)结合一维和二维RGFM界面处理方法应用于多介质球(轴)对称水下爆炸问题的数值模拟.对于一维方程组(1),r方向采用均匀步长,根据RKDG方法的稳定性条件,时间步长取为 对于二维方程组(2),r方向和z方向均采用均匀步长,时间步长取为 其中CFL=0.3,c为音速. 例1 深水高压气泡爆炸问题 本算例是一个深水高压气泡爆炸问题,气泡内是高压气体,气泡外是水,气泡的半径为1,气体的无量纲初始状态值为uH=0.0,pH=8 290,γ=1.4,ρH=1.27,水的无量纲初始状态值为ρl=1.0,ul=0.0,pl=1.0,N=7.15,A=1.0,B=3 310,计算时刻t=0.004 78时的计算区域为[0,4],网格数为400,t=0.015和t=0.021 2时的计算区域时[0,6],网格数为600,t=0.04时的计算区域为[0,10],网格数是1 000.图1分别给出了密度在不同时刻的分布图,并给出了半径随时间的变化曲线(图2). 图1 密度在半径方向的分布图 图2 半径随时间的分布图 例2 圆柱形容器内水下爆炸问题 本算例是容器内气泡爆炸的轴对称问题,圆柱形容器的半径为0.044 45 m,高度为0.228 6 m,在容器中心有一个高压气泡,气泡半径为0.015 m,气泡外是水,气泡内气体的初始状态值为ρH=1 770 kg/m3,uH=0.0 m/s,vH=0.0 m/s,pH=2.0×109Pa,γ=2.0,气泡外水的初始状态值为ρl=1 000 kg/m3,N=7.15,ul=0.0 m/s,vl=0.0 m/s,pl=105Pa,A=105Pa,B=3 310×105Pa,计算区域为r×z∈[0,0.044 45]×[-0.114 3,0.114 3],网格数为70×360,在容器壁处采用反射边界条件,图3分别给出了不同时刻压力的等值线图. (a) t=10 μs (b) t=30 μs (c) t=50 μs图3 不同时刻压力的等值线图 例3 近水面水下爆炸问题 此问题是一个轴对称问题,用固壁代替自由面,计算区域是[0,9]×[-9,3],网格数是270×360,y=3处为固壁,高压气泡位于(0,0)点,半径为1,固壁处采用反射边界,其他边界为自由边界.气泡的初始状态值为ρH=1 270 kg/m3,uH=0.0 m/s,vH=0.0 m/s,pH=8.29×108Pa,γ=2.0,周围水的初始状态值为ρl=1 000 kg/m3,ul=0.0 m/s,vl=0.0 m/s,pl=105Pa,N=7.15,A=105Pa,B=3 310×105Pa.图4~图9分别给出了不同时刻压力,r方向和z方向的速度等值线图. 图4 t=2.0 ms时刻压力的等值线图 图5 t=2.0 ms时刻r方向速度的等值线图 图6 t=2.0 ms时刻z方向速度的等值线图 图7 t=4.0 ms时刻压力的等值线图 图8 t=4.0 ms时刻r方向速度的等值线图 图9 t=4.0 ms时刻z方向速度的等值线图 本文给出了可压缩多介质流动球对称和轴对称问题的数值模拟方法,利用RGFM方法将多介质问题转化为单介质问题,并利用RKDG方法求解欧拉方程.对于水下爆炸问题中出现的空化现象,采用等熵的单流体空化模型进行处理.数值试验结果表明,该算法可大大减少计算量,有效捕捉各种物理现象. [1] COCKBURN B,SHU C W.TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws.II.General framework[J].Mathematics of Computation,1989,52(186):411-435. [2] COCKBURN B,LIN S Y,SHU C W.TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws III:one-dimensional systems[J].Journal of Computational Physics,1989,84(1):90-113. [3] COCKBURN B,HOU S,SHU C W.The Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws.IV.The multidimensional case[J].Mathematics of Computation,1990,54(190):545-581. [4] COCKBURN B,SHU C W.The Runge-Kutta discontinuous Galerkin method for conservation laws V:multidimensional systems[J].Journal of Computational Physics,1998,141(2):199-224. [5] FEDKIW R P,ASLAM T,MERRIMAN B,et al.A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the ghost fluid method)[J].Journal of Computational Physics,1999,152(2):457-492. [6] LIU T G,KHOO B C,YEO K S.Ghost fluid method for strong shock impacting on material interface[J].Journal of Computational Physics,2003,190(2):651-681. [7] WANG C W,LIU T G,KHOO B C.A real ghost fluid method for the simulation of multimedium compressible flow[J].SIAM Journal on Scientific Computing,2006,28(1):278-302. [8] LIU T G,KHOO B C,XIE W F.Isentropic one-fluid modelling of unsteady cavitating flow[J].Journal of Computational Physics,2004,201(1):80-108. [责任编辑 王新奇] A High Precision Numerical Simulation Method for theSymmetric Problem of Multi Media Balls (Shaft) LIU Xiao-xiao (School of science, Nanjing University of Aeronautics & Astronautics, Nanjing 211106, China) In this paper, a high precision numerical simulation method for the flow problem of spherical symmetric and axisymmetric multimedia is presented. At the interface, the RGFM (Real Ghost Fluid Method) method is used to track the interface and define the boundary conditions. The multi medium flow problem is transformed into the single medium flow problem, and the calculation is carried out by using the high precision RKDG (Runge-Kutta Discontinuous Galerkin) method. The single fluid cavitation model with equal entropy is used to deal with the problems of the phenomenon of cavitation during the underwater explosion. The numerical experiment results show that the method can effectively capture all kinds of physical phenomena, keep the interface clear, and greatly improve the computational efficiency. multimedia; symmetry; RKDG (Runge-Kutta Discontinuous Galerkin); RGFM (Real Ghost Fluid Method); cavitation 1008-5564(2016)04-0011-06 2016-01-15 刘肖肖(1988—),女,山东济宁人,南京航空航天大学理学院硕士研究生,主要从事计算流体力学研究. O351 A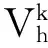
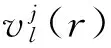


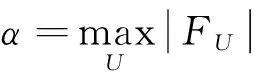


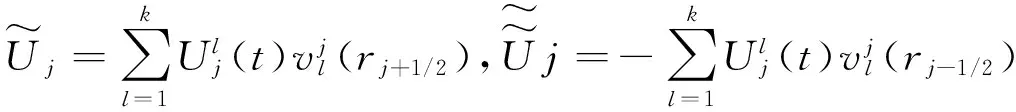
3 数值实验







4 结论

