基于多项式拟合法北斗三频周跳探测改进技术研究

王耀鼎,刘文祥,王飞雪

(国防科学技术大学 电子科学与工程学院,长沙 410073)



基于多项式拟合法北斗三频周跳探测改进技术研究

王耀鼎,刘文祥,王飞雪

(国防科学技术大学 电子科学与工程学院,长沙 410073)

传统三频线性组合的周跳检测量一般通过历元间作差产生,这样要求组合后必须保证不含几何距离,使得线性组合的方式存在一个强约束,很多具有优良特性的单纯载波相位组合无法使用。而将多项式拟合法应用到三频线性组合载波后,则无需限制组合无几何约束。静态场景下,本文提出了一种基于多项式拟合法的三频周跳探测改进算法,通过定义电离层放大因子、钟差放大因子以及组合噪声/波长放大因子,选择出三组线性组合,以此来探测周跳。实测结果表明,本算法可以有效的探测出1周的小周跳。

北斗系统;周跳探测;三频线性组合;多项式拟合法;放大因子

0 引 言

利用载波相位测量值进行高精度导航定位的前提是对周跳进行预处理。北斗三频数据的出现,为周跳的探测与修复提供了更多具有电离层延迟小、波长长、组合噪声小的组合[1]。国内外很多专家学者均对三频周跳探测与修复技术展开了研究。

文献[2]和文献[3]通过检查大周跳、小周跳、特殊周跳三级检测法最终将所有周跳组合检测出来。文献[4]利用三频伪距/载波组合探究了周跳探测算法在GEO、IGSO、MEO三种不同卫星下的探测效果。文献[5]利用空间搜索法探测周跳。文献[7]通过定义波长参数、电离层参数、噪声参数,并以此为目标函数进行周跳探测。文献[8]和文献[9]通过电离层两次历元间作差,削弱了电离层延迟对周跳探测精度的影响。文献[10]分析了不同采样间隔下无几何相位组合和伪距/相位组合的探测性能。文献[11]推导了组合观测值电离层比例因子和噪声比例因子的关系。文献[12]提出将观测数据进行平滑之后再进行周跳探测。文献[13]提取了伪距多路径误差,改善探测精度。文献[14]探测方法对采样间隔较大、电离层较活跃的场景下有较强的适应性。

静态场景下,可以考虑用多项式拟合星地距离。通过线性组合,扩大组合后波长,降低了接收机钟差对探测结果的影响。实测结果表明,本算法可以有效的探测出1周的小周跳。

1 多项式拟合法原理

多项式拟合法基于观测量平滑变化,此时对于观测量可以用一个多项式进行拟合。由于星地距离4次差分后残差已接近于白噪声,因此可利用4阶多项式对观测量进行拟合。其拟合模型为

φi= a0+a1(ti-t0)+a2(ti-t0)2+

a3(ti-t0)3+a4(ti-t0)4

(1)

式中: φi为时刻的载波相位； ai,i=0,…,4为多项式拟合系数； t0为拟合窗口起始时间； ti为拟合窗口内i时刻。目前文献一般利用多项式拟合法直接对单频原始载波相位进行拟合。对于北斗三频载波相位,进行线性组合后,其组合结果并不破坏原始载波相位的平滑性。因此,本文提出将多项式拟合法应用于三频线性组合后的载波相位,对组合后载波相位进行多项式拟合。

2 实数线性组合约束

首先写出原始载波相位观测值表达式:

φ= λφ=r+c(δtu-δts)-I+

T+εφ-λN,

(2)

φi,j,k=iφ1+jφ2+kφ3.

(3)

波长为

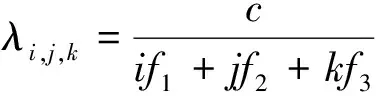
(4)

定义频率无关量为

s=r+c(δtu-δts)+T.

(5)

则将式(2)展开,得:

∑tempρ·(-Ntemp),

tempρ=i,j,k; temp=1,2,3.

(6)

可以通过限制组合系数(i,j,k),使得式(6)中的某一项置零。

考虑周跳探测的误差来源,提出如下无电离层、无钟差、最小组合噪声三种约束。

2.1 无电离层约束

限制组合后电离层系数为0,经过化简,得无电离层组合约束为

(7)

对于北斗系统,可得:

i+1.293j+1.231k=0.

(8)

满足上式的实数解即可满足无电离层约束。

定义式(8)为电离层放大因子αi,j,k,其表达式为

αi,j,k=i+1.293j+1.231k.

(9)

其实际上构成了一个以(i,j,k)为自变量的空间中的平面,则空间中越靠近该平面的点,其对应组合后的电离层放大因子越小。

2.2 无钟差约束

限制组合后钟差系数为0,即非频率部分系数为0,得无钟差约束为

if1+jf2+kf3=0,

(10)

代入数值,得:

763i+590j+620k=0.

(11)

满足上式的(i,j,k)可以消除钟差,其同样定义了一个平面,空间中越靠近该平面的点其钟差影响越小。

定义钟差放大因子为βi,j,k,其值为上式相对于f1的放大倍数

(12)

代入数值,得

βi,j,k=i+0.7733j+0.8126k.

(13)

该值越小,钟差影响越小。

2.3 最小组合噪声约束

定义以周为单位的组合噪声放大因子为

(14)

由上式可知,(i,j,k)在空间中越靠近原点,噪声放大因子越小。

(15)

上式值越小,说明噪声放大程度越小于波长放大程度,则性能越好。

3 最优整数组合

为保证组合后的模糊度为整数,载波组合系数必须为整数。因此需要在整数范围内搜索能够最大限度接近第2节描述的三种约束条件的整数组合。同时,为便于周跳探测,组合后的波长应尽可能长。将整数组合进行分类,定义组合系数之和为M,即:

M=i+j+k.

(16)

同时,定义Mx为满足i+j+k=±x的(i,j,k)的类,由此可以得到多类Mx,由文献[1]可知,M0类和M1类具有优良的特性,而在进行周跳探测时,只需要构造三组线性无关的组合即可。因此,研究M0类和M1类中的组合已经满足要求,故不需再考虑其他类。

3.1 M0类

此时i+j+k=0,由于噪声放大因子不可过大,因此,限制(i,j,k)∈[-5,5]进行搜索,挑选其中的较优组合如表1所示.

表1 M0类组合

为提高多项式拟合法精度,应选择电离层放大因子、钟差放大因子及噪声放大因子均较小的量。

由表1可知,(0,-1,1)是最佳选择,因此,将其确定为第一个线性组合。对于多项式拟合法,接收机钟差对其影响较大,因此需选择钟差放大因子较小的组合。考察组合(1,4,-5),其钟差放大因子在剩余组合中最小,虽然其噪声放大因子较大,但其噪声/波长放大因子γi,j,k较小,因此其性能仍然较好,故选择其为第二个线性组合。

由于限制i+j+k=0,因此M0类中最多有2个线性独立的组合,故第三组组合需要从M1类中进行选择。

3.2 M1类

此时i+j+k=±1,同样,为防止噪声放大因子过大,限制(i,j,k)∈[-5,5]进行搜索,挑选其中的较优组合如表2所示。

表2 M1类组合

由上表可知,噪声放大因子最小的组合是(1,0,0)(0,1,0)(0,0,1),但是其噪声/波长放大因子γi,j,k较大,故不采用。对于组合(-4,2,3),其钟差放大因子及噪声/波长放大因子均最小,虽然电离层放大因子较大,但是由于在产生检测量时用多项式拟合法,因此对于电离层变化不太大的情况,其电离层延迟变化可以很好的通过多项式拟合法消弱其影响。综上,第三组线性组合选择为(-4,2,3)。

4 改进算法流程

由第三节分析可知,选择的载波相位组合系数为(0,-1,1),(1,4,-5),(-4,2,3),假设其组合后的检测量为L,则其周跳组合表达式为

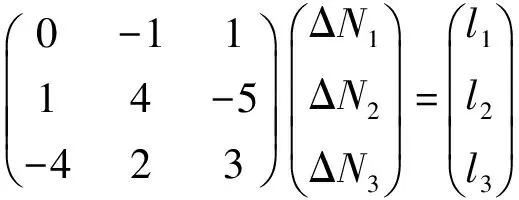
(17)

式中:ΔNi为各频点的周跳值; li为各线性组合的周跳检测量。由于系数矩阵行列式为1,故矩阵是可容许的,则由上式可以解算出各个频点的周跳值,其表达式为

(18)

以第一组线性组合为例,介绍改进算法周跳检测量的产生过程。

根据式(1)和式(3),对组合后载波相位φi,j,k进行多项式拟合,窗口宽度取6,得到多项式系数。

预测第7个历元的组合观测值,其预测值为

a3(t7-t0)3+a4(t7-t0)4,

(19)

φ0,-1,1=0·φ1+(-1)·φ2+1·φ3,

(20)

则周跳检测量l1为

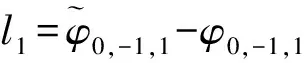
(21)

另外两组线性组合的周跳检测量产生过程与之完全相同,不再赘述。

对li直接取整,即为周跳检测值。

5 实测数据验证

利用北斗一期监测接收机2015年12月22日9时至15时的观测数据,采样间隔为1 s.选取C09卫星进行研究。图1示出了三种组合的周跳检测量情况。

为测试改进算法对特殊周跳(1,1,1)的检测性能,在三个频点400历元处均加入1周小周跳,结果如图2所示。

图1 三种组合的周跳检测量

图2 改进算法三种组合的周跳检测量

理论上三种组合在400历元处的检测量为0,0,1,实际结果为-0.0079,0.0231,1.0470,取整后结果符合理论值。

随机在某些历元加入模拟周跳,其周跳探测情况如表3所示。

对应的周跳探测结果图，如图3所示。

图3 模拟周跳三种组合的检测量

表3 模拟周跳探测与修复结果

6 结束语

在静态场景下,星地距离可以很好的用多项式进行拟合。利用多项式拟合法对组合后载波进行周跳探测,使得组合后观测值即保持了以周为单位的载波的组合系数的整数特性,又可以不再限制几何距离无关,这为探讨新的具有优良特性的线性组合方式开辟了道路。通过限制钟差放大因子和噪声/波长放大因子,选择了三组载波几何相关组合,取代了伪距/相位组合,充分利用载波测量的高精度特性,提高了探测精度。通过加入模拟周跳,验证本算法可以探测小周跳、特殊周跳、大周跳等周跳类型。该方法可应用于北斗三频非差观测数据中各频点周跳的探测。对于动态场景,由于很难用多项式进行拟合,故如何提高动态场景下的探测精度有待进一步研究。

[1] 张小红,何锡扬.北斗三频相位观测值线性组合模型及特性研究[J].中国科学,2015,45(5):601-10.

[2] 曹新运,王坚.GPS三频非差观测值探测与修复周跳[J].武汉大学学报(信息科学版),2014,39(4):450-457.

[3] CLARA DE LACY M, REGUZZONI M,SANSO F. Real-time cycle slip detection in triple-frequency GNSS[J].GPS Solutions,2012,16(3):353-362.

[4] 刘俊,何秀凤,刘炎雄.北斗三频非差观测数据的周跳探测与修复[J].大地测量与地球动力学,2014,34(4):117-22.

[5] 黄令勇,宋力杰,王琰,等.北斗三频无几何相位组合周跳探测与修复[J].测绘学报,2012,41(5):763-8.

[6] 常志巧,刘利,何海波.基于最优观测组合的三频周跳探测与修复[C]//CSNC2010第一届中国卫星导航学术年会论文集,2010.

[7] 韩绍伟.GPS组合观测值理论及应用[J].测绘学报,1995,24(2):8-13.

[8] 黄令勇,翟国君,欧阳永忠,等.削弱电离层影响的三频TurboEdit周跳处理方法[J].测绘学报,2015,44(8):840-847.

[9] 黄令勇,翟国君,欧阳永忠,等.三频GNSS电离层周跳处理[J].测绘学报,2015,44(7):717-725.

[10] 谢恺,柴洪洲,王敏.不同采样间隔下的三频周跳探测与修复算法[J].大地测量与地球动力学,2014,34(1):139-143.

[11] 孙保琪,欧吉坤,盛传贞,等.一种适于Compass周跳探测的三频数据优化组合[J].武汉大学学报(信息科学版),2010,35(10):1157-1160.

[12] 范建军,王飞雪,郭桂蓉.GPS三频非差观测数据周跳的自动探测与改正研究[J].测绘科学,2006,31(5):24-26.

[13] 肖国锐,隋立芬,戚国宾,等.大地测量与地球动力学[J].大地测量与地球动力学,2015,35(4):671-675.

[14] 王兴,刘文祥,李柏渝,等.北斗三频非差观测数据周跳探测与修复[J].国防科技大学学报,2015:1-7.

A New Triple-Frequency Cycle Slip Detection Algorithm Based on Polynomial

WANG Yaoding,LIU Wenxiang,WANG Feixue

(CollegeofElectronicScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China)

Traditional methods of Tri-frequency cycle slip detection are based on the difference of epochs, which requires that the combination do not contain geometric distance. And that causes a strong constraint in the combination. When the polynomial fitting applies to the Tri-frequency cycle slip detection, the constraint is relieved. In static case, this novel applies the polynomial to Tri-frequency cycle slip, and defines ionosphere amplification factor、clock bias amplification factor and noise amplification. The results shows that this method can detect at least 1 slip.

BeiDou; cycle slip; tri-frequency Linear combination; polynomial; amplification factor

10.13442/j.gnss.1008-9268.2016.05.016

2016-07-11

P228.4

A

1008-9268(2016)05-0079-05

王耀鼎 (1992-),男,山东滨州人,硕士,研究方向为星基导航与定位技术。

刘文祥 (1981-),男,江西宜春人,博士,讲师,研究方向为星基导航与定位技术。

王飞雪 (1971-),男,福建长汀人,博士,教授,博士生导师,主要研究方向为卫星导航定位、扩频信号处理、电子系统抗干扰。

联系人： 王耀鼎 E-mail: wangyaodingsdu@126.com