基于GIM的Klobuchar电离层模型的精度及影响因素分析

林清莹,郭金运,闫金凤,沈毅,李旺

(1.山东科技大学 测绘科学与工程学院,青岛 266590;2.河海大学 地球科学与工程学院,南京 210098)



基于GIM的Klobuchar电离层模型的精度及影响因素分析

林清莹1,郭金运1,闫金凤1,沈毅1,李旺2

(1.山东科技大学 测绘科学与工程学院,青岛 266590;2.河海大学 地球科学与工程学院,南京 210098)

利用2003年-2014年的GPS广播星历提供的Klobuchar模型的参数,计算得到全球范围内的电离层延迟,以CODE发布的高精度的全球电离层图(GIM)数据作为参考,对Klobuchar模型进行时空精度分析,并探讨太阳活动和地磁活动与模型精度相关性。结果表明:按年份来看,Klobuchar模型精度与太阳活动和地磁活动呈负相关,在太阳和地磁活动剧烈的年份,模型精度较差,反之较好。按月份来看,Klobuchar模型的精度呈现一个半年的周期,在一月份和七月份的精度较高,在四月份和十月份的精度较低。空间上,Klobuchar模型精度在南北半球大致呈现对称分布;在太阳和地磁活动剧烈的年份,在低纬度地区的精度较低,在中高纬度地区精度较高;在太阳和地磁活动平静的年份,模型在全球范围内的精度较好。

Klobuchar模型;GIM;电离层延迟;精度分析;TEC

0 引 言

电离层延迟是导航定位的重要误差源之一,为了获取快速实时的高精度的导航定位,选取合适的电离层改正模型至关重要。双频接收机可以利用双频信号进行改正,是对于单频用户来说,需要依靠Klobuchar模型进行电离层延迟改正。Klobuchar模型经过多年的观测验证被广泛认为是一种计算方便、实用可靠的电离层时延改正的有效算法[1-2]。

Klobuchar模型是依据长时期的观测资料而建立起来的经验电离层模型,适合大范围的电离延迟修正,全球的改正精度约为50%～60%,利用该模型估计区域电离层延迟,那么该模型精度不够理想。但是该模型具有它独特优势,所以很多专家学者对此深入研究并对其修正[3-8]。只有了解Klobuchar模型在全球范围内不同区域和时间的精度情况,才能更有利于对模型的改进和区域化。

以欧洲定轨中心(CODE)发布的高精度的全球电离层图(GIM)数据作为参考,对Klobuchar模型进行精度分析,探讨太阳活动和地磁活动与模型精度的相关性,分析模型在不同时间、不同区域范围内的精度情况,为Klobuchar模型的改进和区域化提供参考。

1 数据和处理方法

本文利用2003年至2014年每一天的GPS广播星历(ftp://cddis.gsfc.nasa.gov/gps)提供的Klobuchar模型的8个参数来计算Klobuchar模型的电离层延迟。CODE发布全球高精度的电离层格网数据(ftp://ftp.unibe.ch/aiub/CODE),采用的函数模型为球谐函数模型,数据的时间分辨率为2 h,空间分辨率为5°×2.5°(经度上间隔5°,纬度上间隔2.5°)。本文计算Klobuchar模型电离层延迟的时间分辨率为2 h,空间分辨率为5°×2.5°.

对Klobuchar模型精度的分析,主要是将Klo-buchar模型的值与CODE做差,得到偏差(偏差较大说明精度较差,偏差较小说明精度较差),对其偏差进行时间和空间的分析,探讨Klobuchar模型在全球范围内的精度情况以及太阳活动F10.7和地磁活动Kp指数对模型精度影响的相关性。

1.1 Klobuchar模型

Klobuchar模型是美国专家Klobuchar在1987年提出针对单频用户的一种电离层延迟的改正方法。该模型由bent模型简化而来[9],将白天的电离层延迟看做余弦函数的中正部分,夜间的电离层延迟看做常数且取值为5 ns[9-11]。该模型表达式为

(1)

式中: A1为夜间的延迟量,取值为5 ns; A2为白天的余弦函数振幅; P为余弦函数的周期项; t为地方时,单位为s; Tp为初始相位,其值为50 400 s.

将电离层延迟转换为TEC的方法为[12-13]:

(2)

式中: f为GPS在L1载波上的卫星信号; c为光速; Tg为电离层延迟。

1.2 球谐函数模型

CODE向全球提供高精度的GIM产品被GNSS用户广泛应用[12-15]。CODE采用球谐函数模型来计算电离层延迟,球谐函数模型是全球的电离层模型中最为常用的一种方法[12]。

CODE利用的函数模型为球谐函数模型,数学表达式为[15-17]

bnmsin(mβ)] ,

(3)

式中: α为地理纬度; β为日固经度; N为最高阶次; Pnm(α)为标准化的勒让德函数; anm和bnm为球谐函数的系数; n为阶数; m为次数。

2 结果与分析

2.1 时间分析

时间方面的分析主要从两个方面进行,一是以年为单位,分析2003-2014年的年精度;二是以月为单位,分析1-12月的月精度。

对每个格网点以年为单位计算了2003-2014年的年均值,统计了每年TEC偏差的最大正偏差和最大负偏差,如表1所示。结合图1和图2可以看出,地磁活动Kp指数在2003年较高,随后开始下降,在2009年达到极小值之后又开始上升,在2014年又达到极大值。太阳活动指数F10.7在2003年的值较大,随后开始下降在2009年达到极小值,之后又开始上升,在2014年达到极大值。Klobuchar模型的精度随时间变化明显,从2003年的最大负偏差的-19.7 TECu逐渐降低至2008年的最大负偏差-3 TECu;从2009年至2014年TEC含量又开始逐渐升高,说明模型在2003年较差,随着年份的增加精度逐渐提高,在2009年精度达到最高,之后精度又开始下降,在2014年精度又变的较差。说明模型的精度与地磁活动和太阳活动成负相关。

表1 2003-2014偏差的年均值的最大值和最小值统计

图1 2003-2014年的地磁活动Kp指数与太阳活动指数F10.7

图2 2003-2014年偏差的年均值

差值的月均值如图3所示,从图3中可以看出,Klobuchar模型的精度与月份的关系明显,一月份至三月份偏差的月均值逐渐增大,四月份至六月份偏差的月均值逐渐减小,七月份至九月份又开始逐渐增大,十月份至十二月份开始逐渐降低;呈现一个半年的周期。结合图3和表2可以看出,在一年中,七月份的精度最高,月均值的最小负偏差为-7.9 TECu;四月份的精度最低,差值月均值的最小值为-14.4 TECu;差值月均值的最大正偏差的变化范围为1 TECu～7.3 TECu,最大负偏差的变化范围为-7.9 TECu～-15.3 TECu,可以看出最大正偏差的变化范围小于最大负偏差的范围。

图3 一月至十二月的偏差月均值

月份一月二月三月四月五月六月七月八月九月十月十一月十二月最大正偏差/TECu5255646331112446627365最大负偏差/TECu-8-116-144-153-119-82-79-102-128-138-116-84

2.2 空间变化的分析

空间精度主要从两个方面进行分析,一是分析2003年至2014年偏差的总均值;二是分析偏差的标准差。

结合图4(MEAN)和表3可以看出,偏差在全球范围内大致以赤道为中心呈南北对称分布;在低纬度地区的Klobuchar模型的值低于CODE的值;在中高纬度地区,Klobuchar模型的值大部分区域高于CODE的值,最大负偏差为-6.2 TECu,最大正偏差为5.2 TECu,最大负偏差小于低纬度地区;在东半球的低纬度地区的偏差的较大,特别是在赤道附近最大负偏差达到了-10.1 TECu.结合图4(STD)和表4可以看出,标准差大致呈现南北半球对称分布;在赤道附近的标准差最大,特别是在东半球的赤道附近,最大值达到了5.8 TECu;由赤道向两极标准差逐渐减小,在中纬

度地区的最大值为3.5 TECu,在高纬度地区最大值为0.4 TECu.由上述可知,Klobuchar模型在全球范围内的精度大致呈南北对称分布,在低纬度地区的精度低,在中高纬地区精度高。

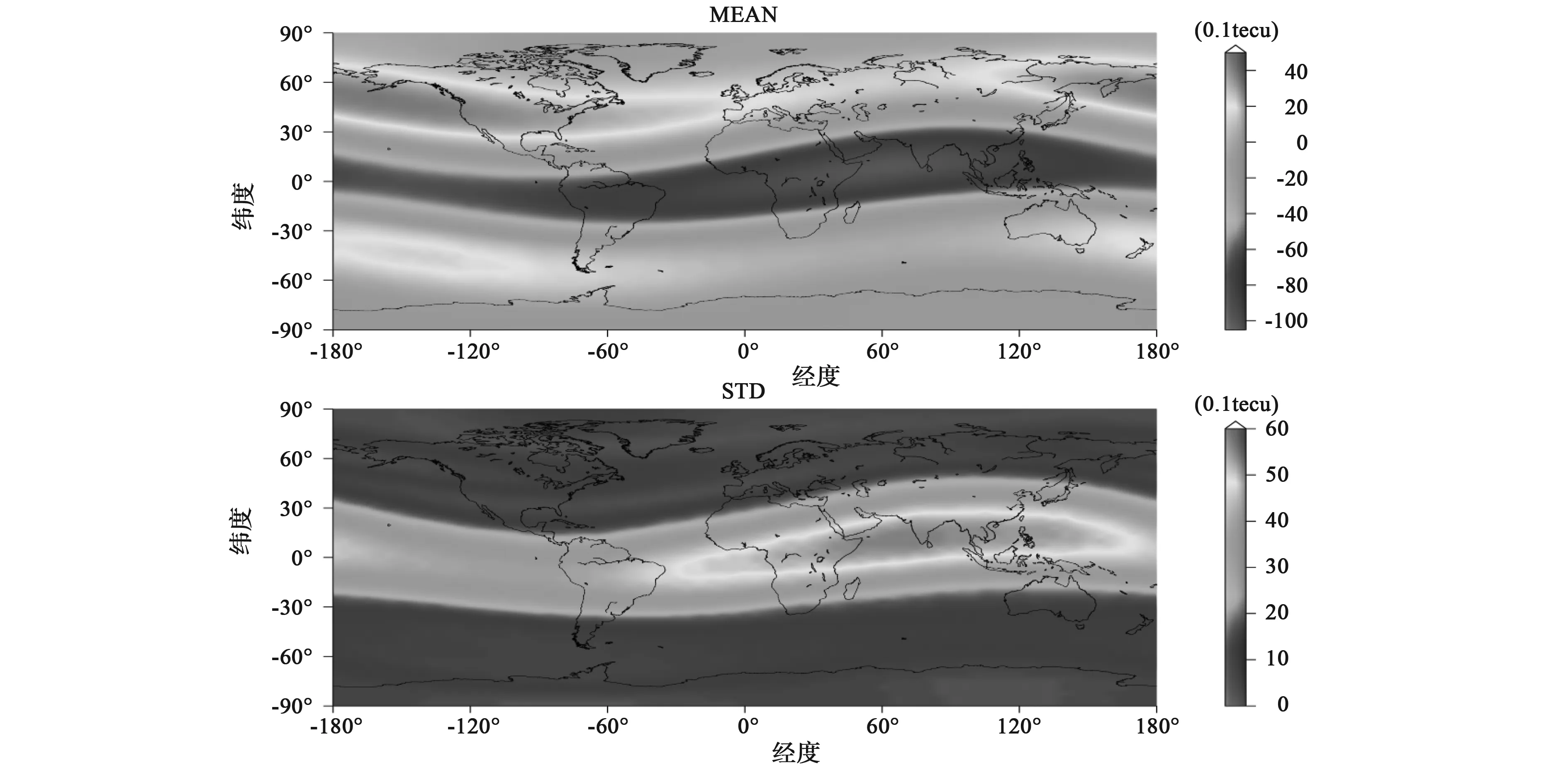
图4 2003-2014年的偏差的均值和标准差

纬度90°N-60°N60°N-30°N30°N-0°0°-30°S30°S-60°S60°S-90°S最大正偏差/TECu485207121905最大负偏差/TECu-07-62-101-95-25-2

表4 2003-2014年的偏差的标准差不同纬度段的最大值的统计

3 结束语

利用2003～2014年的GPS的广播星历计算得到了Klobuchar模型的电离层延迟,以CODE的高精度的电离层格网数据作为参考,分析Klobuchar电离层模型的时间和空间上的精度情况,探讨了模型精度与太阳活动和地磁活动的相关性,结果表明:

1) 按年份来看,太阳活动和地磁活动与Klobuchar模型的精度呈负相关。在太阳和地磁活动平静的年份,模型的精度较高;在太阳活动和地磁活动剧烈的年份,模型的精度较低,并且对低纬度地区的影响大于中高纬度地区。

2) 按月份来看,Klobuchar模型的精度与月份有关,并且呈现半年周期,一月份和七月份精度较高,四月份和十月份精度较低;一年中,七月份的精度最高,四月份的精度最低;

3) 空间上,Klobuchar模型精度在南北半球大致呈对称分布,在太阳和地磁活动较高的年份,低纬度地区的精度低,中高纬度精度较高;在太阳和地磁活动平静的年份,模型在全球范围的精度较高。

Klobuchar模型由于其特有的优势,很多专家学者让对其进行不断研究,但是大部分是研究模型的小范围区域化改进,如何大范围的区域改进或者全球范围内的模型改进是下一步的研究方向。

[1] 高杨,焦诚,刘萧,等. 利用中国区域电离层数据拟合Klobuchar参数[J].全球定位系统, 2014, 39(5):37-40.

[2] 张勇,张斌,马能武. 单频GPS接收机的电离层延迟改正模型研究[J]. 大地测量与地球动力学, 2012,32(2):69-73.

[3] 章红平. 基于地基GPS的中国区域电离层监测与延迟改正研究[D].上海:中国科学院上海天文台, 2006.

[4] YUAN Y B, LI Z S, WANG N B, ZHANG B C,etal. Monitoring the ionosphere based on the crustal movement observation network of China [J]. Geodesy and Geodynamics, 2015, 6(2):73-80.

[5] 章红平,平劲松,朱文耀, 等. 电离层延迟改正模型综述[J]. 天文学进展, 2006, 24(1):16-26.

[6] 李维鹏,李建文,戴伟. LOBUCHAR K电离层延迟改正模型精化方法的研究[J].测绘科学, 2015, 34(5):49-51.

[7] 牛飞,马刘海,刘芹,等. 电离层异常状态下的自适应平滑滤波算法及性能分析[J].测绘科学技术学报, 2015,32(4):331-335.

[8] 蔡成辉,刘立龙,黎峻宇, 等. 基于改进的Klobuchar模型家里南宁市区域电离层延迟模型[J]. 大地测量与地球动力学, 2015, 35(5):797-800.

[9] 杨哲,宋淑丽,薛军琛, 等. Klobuchar模型和NeQuick模型在中国地区的精度评估[J].武汉大学学报(信息科学版), 2012, 37(6):704-707.

[10] KLOBUCHAR J A. Ionospheric time-delay algorithm for single-frequency GPS users[J]. IEEE Transactions on Aerospace and Electronic Systems, 1987, 23 (3): 325-331.

[11] 郭金运,宗干,李旺, 等. GPS单星单历元模糊度与电离层延迟分类解算[J].山东科技大学(自然科学版), 2015, 34(1):54-59.

[12] 王军,党亚民,薛树强.NeQuick电离层模型在中国地区的应用[J]. 测绘科学,2007(4):38-40.

[13] 陈鹏,陈家君. 全球电离层格网模型精度影响因素分析[J]. 大地测量与地球动力学, 2014, 34(2):106-113

[14] WANG L, GUO J Y, YU X M,etal. Analysis of ionospheric anomaly preceding the Mw7. 3 Yutian earthquake[J]. Geodesy and Geodynamics, 2014,5(2): 54-60.

[15] 余明,郭际明,过静珺. GPS电离层延迟Klobuchar 模型与双频数据解算值的比较与分析[J]. 测绘通报, 2004(6):5-8.

[16] GUO J Y, WANG L, LIU X,etal. Temporal-spatial variation of global GPS derived total electron content, 1999-2013 [J]. PloS One, 2015, 10(7). doi:10.1371/Journal.pone.0133378.

[17] 李征航,黄劲松. GPS测量与数据处理[M].2版.武汉:武汉大学出版社, 2010.

Precision and Influential Factors Analysis of Klobuchar IonosphericModel Based on GIM on Global Scale

LIN Qingying1,GUO Jinyun1,YAN Jinfeng1,SHEN Yi1, LI Wang2

(1.CollegeofGeodesyandGeomatics,ShandongUniversityofScienceandTechnology,Qingdao266590,China；2.SchoolofEarthScienceandEngineering,HehaiUniversity,Nanjing210098,China)

The Klobuchar model parameters provided by GPS broadcast ephemeris of the year of 2003-2014 were used to calculate the global ionospheric delay, and then analysed the precision of the Klobuchar model by referring high-precision global ionospheric maps (GIM) data issued by CODE, and explore the accuracy of the model correlated with the solar activity and geomagnetic activity. The results showed that Klobuchar model accuracy with solar activity and geomagnetic activity was negatively correlated according to the mean results of years’ difference value. The period of Klobuchar model's precision is six-months and precision of model is higher in January and July and lower in April and October according to the mean results of months’ difference value. Precision of Klobuchar model presents roughly symmetrical distribution in north-south hemispheres with low precision in the low latitudes and comparatively high precision in the mid-high latitudes in the spatial distribution, in solar and geomagnetic activity calm year, model accuracy are similar on global scale.

Klobuchar model; GIM; ionospheric delay; precision analysis; TEC

10.13442/j.gnss.1008-9268.2016.05.019

2016-06-06

国家自然科学基金(批准号:41374009);山东省自然科学基金(批准号:ZR2013DM009);科技基础性工作专项(编号:2015FY310200)

P228

A

1008-9268(2016)05-0093-06

林清莹 (1989-),男,山东枣庄人,硕士生,主要从事电离层延迟研究。

郭金运 (1969-),男，山东菏泽人,博士、教授、博导,主要从事空间大地测量、海洋大地测量和物理大地测量等研究。

联系人： 林清莹 E-mail: Linqy0094@163.com