在初三几何教学中如何强化对称意识

广东省佛山南海实验中学(528200)黄业青

在初三几何教学中如何强化对称意识

广东省佛山南海实验中学(528200)黄业青

《义务教育课程标准实验教科书(2001年)·数学》(北京师范大学出版社)教材采取螺旋式上升的方式编排知识点,满足学生循序渐进的发展需求,对对称的知识的处理也是这样.在初三几何中,对称知识体现在九上第一章《特殊平行四边形》、九下第三章《圆》,涉及到菱形、矩形、正方形的性质和圆的垂径定理等等.到了初三阶段,学生应该习得利用对称的审美达到探索新知识、发现新结论、解决新问题的能力.

1．动手操作,经历利用对称探索新知识过程,体会对称的重要性

(1)九年级上册第一章《特殊平行四边形》第1节《菱形的性质》,在教授“菱形的性质”知识点时,让学生动手操作,通过折纸、画图,探索发现菱形的四条边相等、菱形的对角线互相垂直.

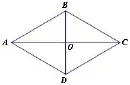
图1　

课前准备:让学生剪一个菱形.

课堂活动:用菱形纸片折一折,思考下列问题:

①菱形是轴对称图形吗?如果是,它有几条对称轴?对称轴之间有什么位置关系?

②菱形中有哪些相等的线段?

课堂总结:小组代表汇报,小结结论.

教师总结:图形的对称美可以发现图形有相应简洁的结论,如菱形有2条对称轴,相应有2个特殊的结论——菱形的四条边相等、菱形的对角线互相垂直.

(2)九年级上册第一章《特殊平行四边形》第3节《矩形的性质》,在教授“矩形的性质”知识点时,让学生动手操作,通过折纸、画图,探索发现矩形的四个角相等、矩形的对角线相等.

课前准备:让学生剪一个矩形.

课堂活动:用矩形纸片折一折,思考下列问题:

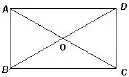
图2　

①矩形是轴对称图形吗?如果是,它有几条对称轴?

②矩形中有哪些相等的线段?

课堂总结:小组代表汇报,小结结论.

教师总结:图形的对称美可以发现图形有相应简洁的结论,如矩形有2条对称轴,相应有2个特殊的结论,即矩形的四个角相等、矩形的对角线相等.

(3)九年级上册第一章《特殊平行四边形》第1节《正方形的性质》,在教授“正方形的性质”知识点时,让学生动手操作,通过折纸、画图,探索发现正方形的四条边相等、四个角相等、正方形的对角线相等、正方形对角线互相垂直.

课前准备:让学生剪一个正方形.

课堂活动:用正方形纸片折一折,思考下列问题:

①正方形是轴对称图形吗?如果是,它有几条对称轴?

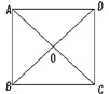
图3　

②正方形中有哪些相等的线段?

课堂总结:小组代表汇报,小结结论.

教师总结:图形的对称美可以发现图形有相应简洁的结论,如正方形有4条对称轴,相应有4个特殊的结论,即正方形的四条边相等、四个角相等、正方形的对角线相等、正方形对角线互相垂直.

(4)九年级下册第三章《圆》第8节《垂径定理》,在教授“垂径定理”知识点时,让学生动手操作,通过折纸、画图,探索垂径定理的结论.

课前准备:以小组为单位发给学生右图的基本图形.

课题活动:学生折一折,思考下列问题:

①这个图形是轴对称图形吗?有多少条对称轴?

②有哪些线段相等?

图4　

课题总结:小组代表汇报,小结结论.

教师总结:轴对称图形对应的线段相等.

2.回顾对称的典型例子,强化对称意识.

回顾初一初二一些经典定理和结论的证明,强化学生对对称的理解.

(1)回顾八年级下册第六章《平行四边形》的三角形中位线定理,证明这个定理为何这样作辅助线,对称的意识就是来源.

已知:如图,DE是△ABC的中位线．

图5　

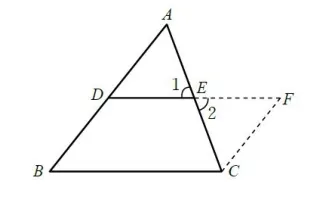
图6　

此题证明的思路是构造平行四边形,但是为何这样构造呢?因为要证明DE是BC的一半,可以将DE延长两倍,此时将△ADE绕着点E旋转180°,即作△ADE关于点E的中心对称图形,便有证明的思路了.通过回顾典型定理的证明,发现经典的证明也用到对称的意识,强化学生对对称的理解.

(2)回顾定理的证明:在直角三角形中,30°所对的直角边是斜边的一半.

已知:在Rt△ACB中,∠BAC= 30°

图7　

此题证明的思路是构造等边三角形,但是为何这样构造呢?因为要证明BC是AB的一半,可以将BC延长两倍,此时做△ABC关于AC的轴对称图形,便有证明的思路了.通过回顾典型定理的证明,发现经典的证明也用到对称的意识,强化学生对对称的理解.

3.利用对称解题,强化对称意识.

学生经历利用对称探索发现结论过程和回顾一些经典定理、结论的证明,强化了对称的意识,此时让学生利用对称解题,进一步强化对称的意识.

(1)如图,AD是锐角△ABC的高,其中AB+BD= CD,求证:∠B=2∠C

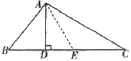
图8　

分析:这个证明题中,只有AB+BD=CD和AD是高这两个条件,那么可以思考是否能根据对称创设另一个关于线段的关系,可以相互替代,从而证明角之间的关系.可以考虑作AB关于AD的对称线段AE,创建一个轴对称图形,这样找到了证明的思路.

(2)如图,在△ABC中,∠A=90°,点D是BC中点,点E,F分别在AC、AB上,且∠EDF=90°,试说明: BF2+CE2=EF2.

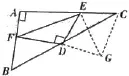
图9　

分析:要求证明三角形中边的关系,并且三条边不在一个三角形中,因此,考虑如何创设一个三角形,并且利用边角的关系来证明.作△BFD关于点D的中心对称图形,作EF关于DE的轴对称图形,便可以发现△BFD和△CDG全等,得到GE=ER,BF=CG,进而得到证明的思路.

这样,学生利用对称解题,进一步强化了对称的意识,体会到对称之美,美在内在的思维.

紧扣教材,根据学生认知的特点和规律,采取螺旋式上升的教学原则,从这三个方面即把握教材学生探索发现、回顾经典强化对称意识、利用对称解题进一步强化对称意识,从而有效地强化学生的对称意识,达到将美学原理应用于解题实践达到以美启智,提高学生解决问题的能力,提升了学生数学素养.