信道编码技术新进展

白宝明，孙 成，陈佩瑶，张 冀

(西安电子科技大学 综合业务网理论及关键技术国家重点实验室，陕西 西安 710071)



信道编码技术新进展

白宝明，孙 成，陈佩瑶，张 冀

(西安电子科技大学 综合业务网理论及关键技术国家重点实验室，陕西 西安 710071)

信道编码是可靠通信系统中不可或缺的一个环节。从逼近Shannon容量限的角度介绍了信道编码技术的发展历史及现状，描述了几种重要的信道编码方法。重点论述了Turbo码、多元LDPC码、LDPC卷积码和Polar码等可逼近信道容量的现代编码方案，给出了这几种码的特点以及它们在深空通信、5G通信系统和光通信系统中的应用。

信道编码；逼近容量；应用；5G

0 引言

自1948年Shannon创立信息与编码理论这一学科以来，在不可靠信道上实现可靠通信所必需的信道编码技术得到了广泛的关注和深入的研究，目前它已作为一项标准技术而广泛应用于各类数字通信系统和数据存储系统。Shannon于1948年在贝尔系统技术杂志发表的《通信的数学理论》的长篇论文中[1]，首次提出了通信系统模型，并指出系统设计的中心问题是在干扰噪声中如何有效而可靠地传送信息；同时，他指出可以用编码的方法实现这一目标。在这篇论文中，Shannon首次提出了熵与信道容量的概念。并指出：任一个通信信道都有一个参数C，称之为信道容量，如果信息传输速率R小于C，则存在一种编码方法，当码长充分长时，系统的错误概率可以达到任意小。这就是著名的信道编码定理。此后，构造可达到信道容量或者可逼近信道容量(Shannon限)的信道编码具体方法及其可实用的有效译码算法一直是信道编码理论与技术研究的中心任务。

在信道编码研究过程中，出现了许多优秀的编码方法，既包括经典编码，如BCH码[2-3]、RS码[4]及卷积码[5]等，也包括现代编码，如Turbo码[6]、LDPC码[7]及Polar码[8]等。

本文将描述信道编码的发展历史及研究现状，介绍信道编码发展中的重要编码方案，重点论述几种可逼近信道容量的现代编码方法及其应用。

1 经典编码的发展

自1948年Shannon论文发表起，在编码方法上，人们先后提出了Hamming码[9]、Muller码[10]、BCH码[2-3]、RS码[4]等线性分组码以及卷积码[5]等经典信道编码。经典编码的编、译码大多是使用代数方法，并以Hamming距离为其性能度量。设计的目标是要最大化码字之间的Hamming距离[11]，从而获得优异的性能。

Hamming码是由Hamming于1950年提出的[9]，它只能纠正一个错误。后来，Hocquenghem在1959年[2]，Bose和Chaudhui在1960年[3]，分别独立地发现了可以纠正多个错误的二进制BCH码。RS码是非二进制BCH码的一个子类，但它们却是由Reed和Solomon于1960年[4]，即发现BCH码的同一年，采用完全不同的方法独立构造出来的。BCH码和RS码均可以采用代数译码算法进行快速有效译码，如BM算法[11]等。RS码不但拥有优异的纠随机错误的能力，而且抗突发错误的能力同样出色，因而被广泛应用于CD、磁盘、Flash等存储领域。

卷积码是由Elias最早在1955年提出的[5]。不同于一般的分组码，卷积码编码器有记忆，即编码器的输出不仅取决于当前时刻的输入，也依赖于之前的输入。Wozencraft和Reiffen给出了卷积码的序列译码算法[12],Fano后来改进了该算法。1963年，Massey提出了一种效率较低但是易于实现的译码方法，即门限译码[13]。卷积码的一个重要进展是1967年Viterbi提出了Viterbi译码算法[14]，1973年Forney证明了Viterbi算法实际上是卷积码的最大似然译码算法。在Linkabit公司和美国国家航天局(NASA)JPL实验室的推动下，Viterbi算法很快成为了NASA深空通信标准的一部分，并且得到了广泛的商用。1974年，Bahl、Cocke、Jelinek和Raviv(BCJR)提出了最大后验概率(MAP)译码算法,也叫BCJR算法[15]。这一算法更进一步地推动了卷积码的应用。如今，BCJR算法已广泛应用于软判决迭代译码中。

上述各信道编码方案，虽然译码复杂度大多在可接受的范围内，然而由于码长较短，其性能受到了限制，一般离Shannon限有较大的距离。为了构造出译码复杂度可接受且差错控制性能优异的长码，Elias在发明卷积码的前一年便提出了乘积码[16]的概念，这是第一个由短码构造长码的方法。乘积码以两个(或多个)码长较短的线性分组码作为分量码进行阵列编码，其码长是各分量码码长的乘积，译码可通过对各分量码单独译码从而得到次优的结果。1966年，Forney提出了另一种由短分量码构造长码的编码方案：(串行)级联码[17]。级联码通过将内码和外码进行串行级联，在不增加译码复杂度的同时获得较大的性能提升。上世纪70年代，NASA采用以卷积码为内码(并用Viterbi译码)、RS码为外码的级联码作为深空通信的信道编码标准，在理论上展示了这种码距离Shannon限在3 dB以内，并在实际中取得了极好的效果。人们将深空通信与编码的结合称为“天仙配”。这是第一个构造出并在实际中使用的比较接近Shannon限的好码。

2 现代编码

现代编码始于1993年。在那一年的IEEE国际通信(ICC)会议上，来自法国ENST Bretagne的Berrou等人提出了对于信道编码界具有革命性意义的Turbo码[6]。从此，信道编码翻开了历史新的一页，进入了一个崭新的阶段。

Turbo码问世后不久，剑桥大学的MacKay[18]和MIT的Spielman等人几乎同时发现：Gallager早在1962年提出的低密度校验(LDPC)码在迭代译码算法下也能逼近信道容量。这些成果使得沉寂30多年的LDPC码重新焕发活力，同时迅速引发了又一轮对迭代译码研究的热潮。在之后的研究中，又提出了多种逼近信道容量的好码，如多元LDPC码[19]、空间耦合LDPC码[20]及Polar码[8]等。现代信道编码一般采用类随机编码方法，并结合迭代软译码以达到逼近最大似然译码性能；一般以与Shannon限的距离来衡量编码方法的性能。下面将主要介绍几种最具代表性的现代编码方法。

2.1 Turbo码

图1给出了CCSDS标准中的Turbo编码器结构。如图所示，Turbo码巧妙地将两个简单的分量码通过伪随机交织器并行级联在一起，以此构造了长码并实现了Shannon随机编码的思想。Turbo码一般选择卷积码为分量码，如果采用分组码作为分量码，则称为Turbo乘积码(或分组Turbo码)。在译码时，两个分量码译码器(对应于两个分量编码器)分别采用软输出译码算法(如MAP算法)进行译码；使用迭代译码，通过在两个分量译码器之间相互传递信息来获得逼近Shannon限的性能。仿真结果表明，码率为1/2的Turbo码在AWGN信道上距离信道容量限仅约0.5 dB。目前Turbo码已广泛应用于各种数字通信系统中，例如：CCSDS的深空通信标准、数字视频广播(DVB)标准、第三代移动通信系统以及3GPPLTE标准。

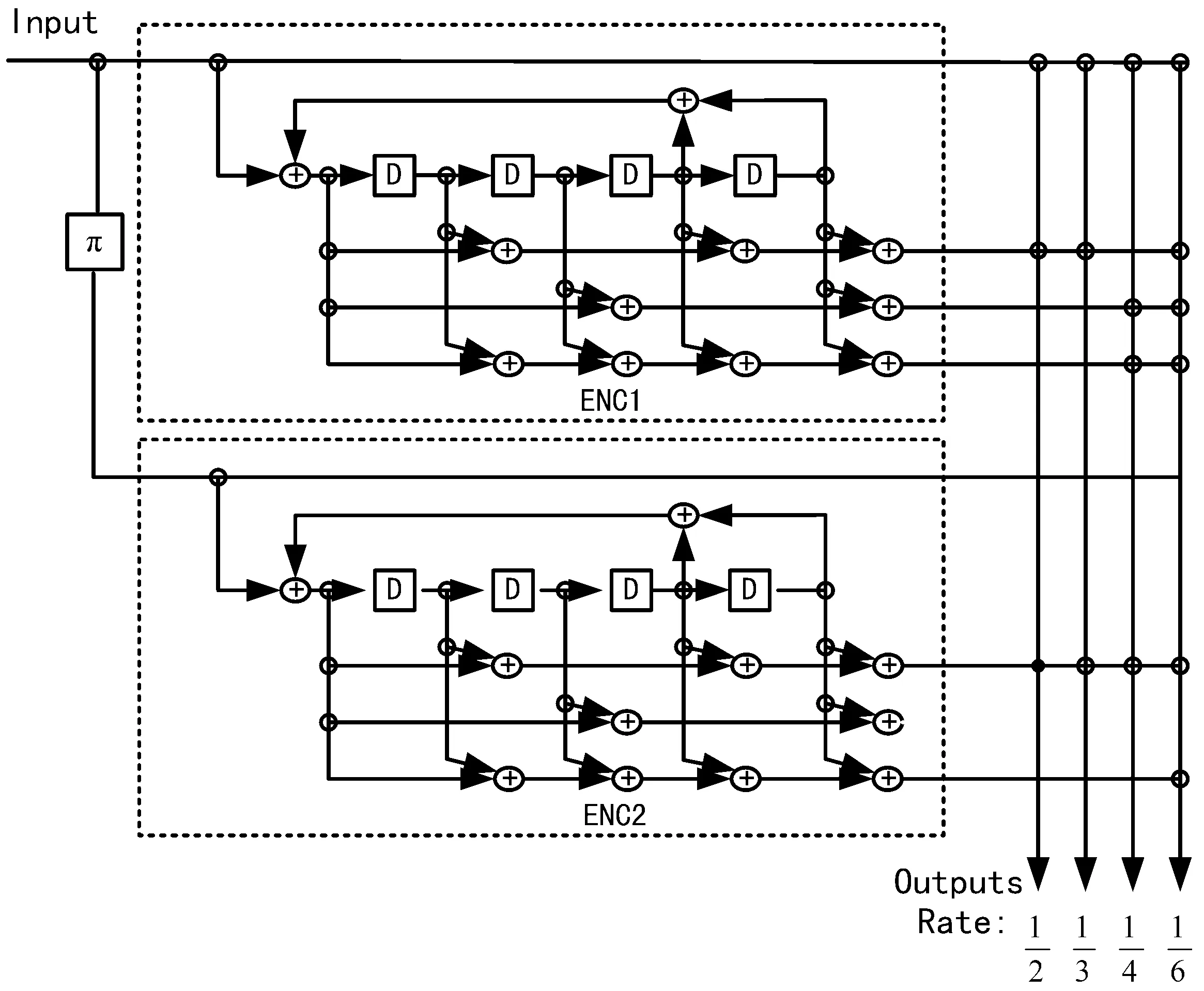
图1 CCSDS建议的Turbo码编码器结构

2.2 二元LDPC码

自LDPC码的再发现[18]以来，它一直是编码工作者研究的热点。目前，在二元LDPC码的构造、编译码方法以及性能分析方面都取得了极大的成果。LDPC码是一类线性分组码，名字中的低密度来源于其校验矩阵的稀疏性，即校验矩阵中只有数量极少的非零元素。相较于Turbo码，LDPC码已被证实有多个优点：① 不需要复杂的交织器，降低了系统的复杂度和系统时延；② 具有更好的误帧率(FER)性能，迎合了现代数字通信的需要；③ 错误平层大大降低，满足了极低误码率通信系统的需求；④ 译码算法为线性复杂度，译码器功耗更小，数据吞吐率更高。

在LDPC码的译码算法方面，Gallager的论文给出了软判决与硬判决两类迭代译码算法(现在称之为和积算法和比特翻转算法)。LDPC码的“再发现”之后，人们对高性能的简化译码算法进行了深入研究，提出了各种在性能与复杂度之间可以很好折中的译码算法，如最小和算法、基于可靠度的译码算法、迭代大数逻辑译码算法等。

研究结果表明：对于码率为1/2的非规则LDPC码，当其码长趋于无穷大时，在二进制输入AWGN信道上进行可靠通信所需的Eb/N0门限值距Shannon限仅为0.004 5 dB[21]。另外，Gallager的工作显示，规则LDPC码的最小距离随码长线性增加，这就保证了在码长充分大时，采用最大似然译码,规则LDPC码不会有错误平层现象。与Turbo类似，二元LDPC码已经成为CCSDS深空通信、光通信及数字视频广播等标准的一部分，得到了广泛的应用。

2.3 多元LDPC码

多元LDPC码最早也是由Gallager在其博士论文中基于模运算提出的[7]。1998年，Davey和Mackay将其推广，提出了定义在有限域GF(q)(q>2)上的多元LDPC码[19]，同时给出了一种q元和积译码算法(Q-ary Sum-product Algorithm，QSPA)。

为方便起见，这里的介绍限于定义在有限域的多元LDPC码。令GF(q)是一个包含q个元素的有限域，其中q是素数的幂次。一个长为n的q元LDPC码是由GF(q)上的m×n稀疏校验矩阵H的零空间所定义的线性分组码，其中m为校验方程的个数(矩阵行数)。这里要求H中的非零元素密度r很低(r定义为矩阵中非零元的个数与元素总个数的比值)。其码率为：

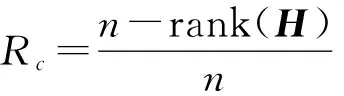
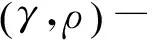
上述两条性质是在迭代译码时性能很好的码的常备条件，其中第①条常称为行列约束(RC-constraint)。

多元LDPC码还可以用Tanner图[22]来表示，Tanner是一个由校验节点和变量节点组成的二部图。校验矩阵H与Tanner图之间的关系如下：校验矩阵H的m行对应于Tanner图的m个校验节点；n列对应于Tanner图的n个变量节点；当且仅当H中的元素hij为非零元素时，Tanner图中第i个校验节点与第j个变量节点相连接。Tanner图中，最短环的长度称为围长(girth)。图2给出了一个多元LDPC码的校验矩阵及其对应的Tanner图表示。

近些年，多元LDPC在构造、译码和分析等方面取得了显著的成果。与二元LDPC码类似，多元LDPC码的构造方法大致可分为两类[23]：① 利用计算机穷搜索的随机或伪随机构造方法；② 基于代数或者组合工具的结构化构造方法。

在译码方面，虽然多元LDPC码具有优秀的性能，但是其较高的译码复杂度一直阻碍着其实际应用，因此多元LDPC码的低复杂度译码算法一直是研究热点和难点。QSPA译码复杂度主要集中在校验节点的更新过程中，因此MacKay和Davey将快速傅里叶变换(FFT)应用于QSPA算法的校验节点的运算，提出了多元LDPC码的FFT-QSPA算法[24]，该算法随后由Barnault等进一步作出完整描述[25]。为了进一步降低复杂度，Declercq等人于2007年提出了扩展最小和(Extended Min-Sum,EMS)译码算法[26]。

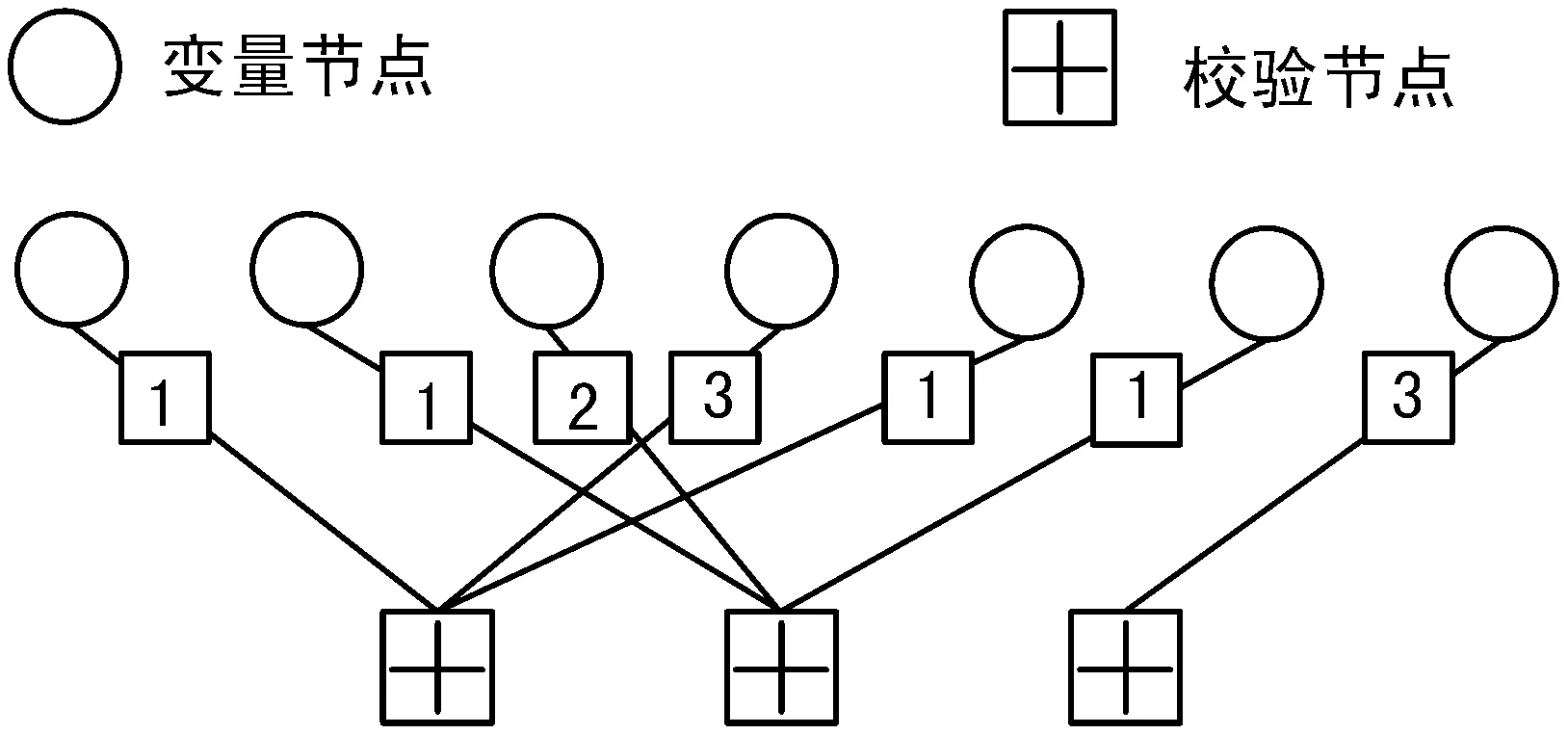
图2 多元LDPC码校验矩阵及其Tanner图

以上算法都是基于概率信息的；另一类复杂度更低的是基于可靠度的译码算法。2010年，Chen-Bai和Zhao-Ma等分别提出了两种低复杂度的基于符号可靠度的译码算法[27-28]。同年，Chen-Huang等也提出了基于迭代软/硬符号可靠度的译码算法[29]。2014年，Huang还研究了一种基于比特可靠度的低复杂度译码算法[30]。表1给出了q元LDPC码的几种代表性译码算法的复杂度。

表1 多元LDPC码的几种代表性译码算法复杂度比较

现有的研究结果表明，相对于二元LDPC码，多元LDPC码有如下优点：① 在中短码长下，多元LDPC码比二元LDPC码具有更优的纠错性能；② 多元LDPC码的抗突发错误能力比二元LDPC码强；③ 多元LDPC码是面向符号的，非常适宜与高阶调制方案结合从而提供更高的数据传输速率和频谱效率。

由此可见，多元LDPC码具有很高的应用价值。欧洲的ENSEA联合三星、意法半导体等诸多公司进行的“达芬奇计划”(DAVINCI Project)，便是围绕多元LDPC码展开的关于多元编码调制系统的研究，旨在为下一代移动通信系统提供更可靠的高频谱效率解决方案。

2.4 LDPC卷积码

上述LDPC码属于分组码，1999年Felstrom和Zigangirov提出了LDPC卷积码及其编译码技术[31]，它可以看作是将一些标准LDPC分组码以链的形式耦合在一起得到的，因而也被称为空间耦合(Spatial Coupling,SC)LDPC码。文献[32]给出了一个码率为R=b/c的LDPC卷积码的半无限检验矩阵的一般形式，如下所示：

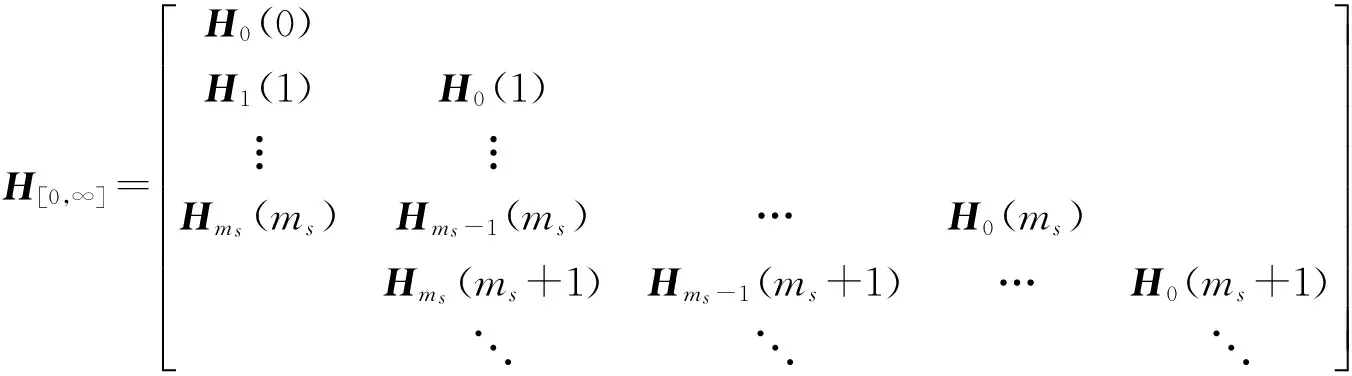
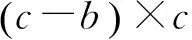
①Hi(t)=0,i<0或者i>ms,∀t。

② 存在t使得Hms(t)≠0。

③H0(t)≠0并且满秩，∀t。

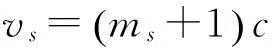
类似于LDPC分组码，LDPC卷积码的校验矩阵也具有稀疏特点，并可以通过基于滑窗结构的迭代译码算法进行译码，因而译码时延小。滑窗译码如图3所示。假设窗口大小W=3，在每个窗口内，采用一般LDPC分组码的译码算法进行译码(如和积算法、SPA)，一个窗口译码结束后，输出目标符号，滑动窗口，进行下一个窗口的译码，依次一直执行下去，直到输出所有符号，译码结束。

LDPC卷积码的性能分析于近几年得到了广泛的研究。Lentmaier和Costello等利用密度进化技术，对SC-LDPC码在BEC和AWGN信道下BP译码的收敛性进行了系统的分析，指出其译码门限优于相应的LDPC分组码[33]。Kudekar、Richardson和Urbanke给出了更多分析结果，证明了在BEC上二元SC-LDPC码的BP译码门限能达到其分量LDPC分组码的最佳MAP译码门限[20]，即分量码的空间耦合能够改进BP译码门限，最终达到“门限饱和”。

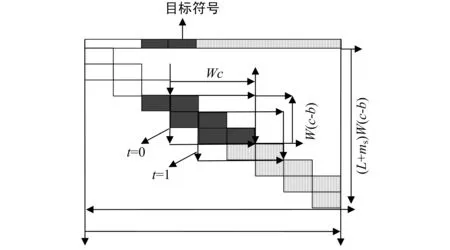
图3 LDPC卷积码的滑窗译码示意图

在文献[34]中，作者证明了在BMS信道上SC-LDPC码集合也表现出门限饱和现象，从而进一步展示了稀疏图码中，“空间耦合”这一结果特性的作用。大量的研究工作表明空间耦合技术对多种信道(BEC、BMS、MAC、Relay)和通信问题都表现出了优异性能。研究表明，具有类似结构的码[35]都具有优异的性能[36-37]。另外，多元空间耦合LDPC码也具有门限饱和现象[38]。Costello 等于2006年将LDPC卷积码同LDPC分组码进行了系统的比较，指出在相同运算复杂度下，LDPC卷积码的纠错性能优于LDPC分组码，并且更适合于不需要将数据分块的连续数据传输系统以及可变帧长的包通信系统，因为它通过结尾处理，可用来构造一类可变帧长码。2008年，Pusane等进一步研究了LDPC卷积码的硬件实现问题[39]，给出了一些硬件实现方案，进一步增强了LDPC卷积码的可应用性。

2.5 Polar码

虽然上述的Turbo码、LDPC码的性能已经非常接近信道容量，但都是通过仿真验证的。2008年，Arikan提出了极化(Polar)码[40]，这是第一个可理论证明达到任意二进制输入离散无记忆对称信道容量(BI-DMC)，也就是可以达到Shannon限的码，并且具有低编译码复杂度。Polar码的核心是“信道极化[8](ChannelPolarization)”。随着码长无限增大，由编译码产生的极化效应，使得多个独立二进制输入信道等效为容量接近于0或1的比特信道，从而信息可在容量接近1的无噪信道上传输。

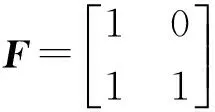
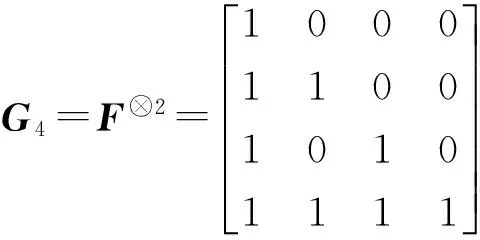
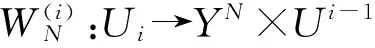
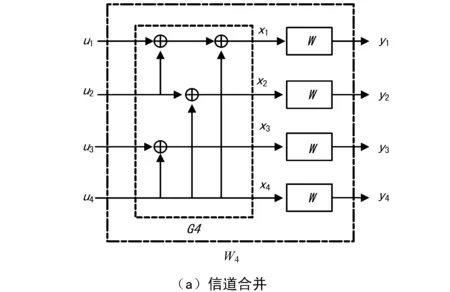
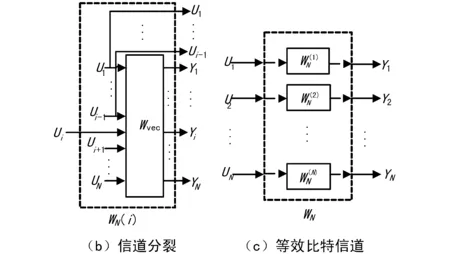
图4 信道合并与信道分裂(由编译码共同完成)

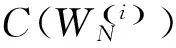
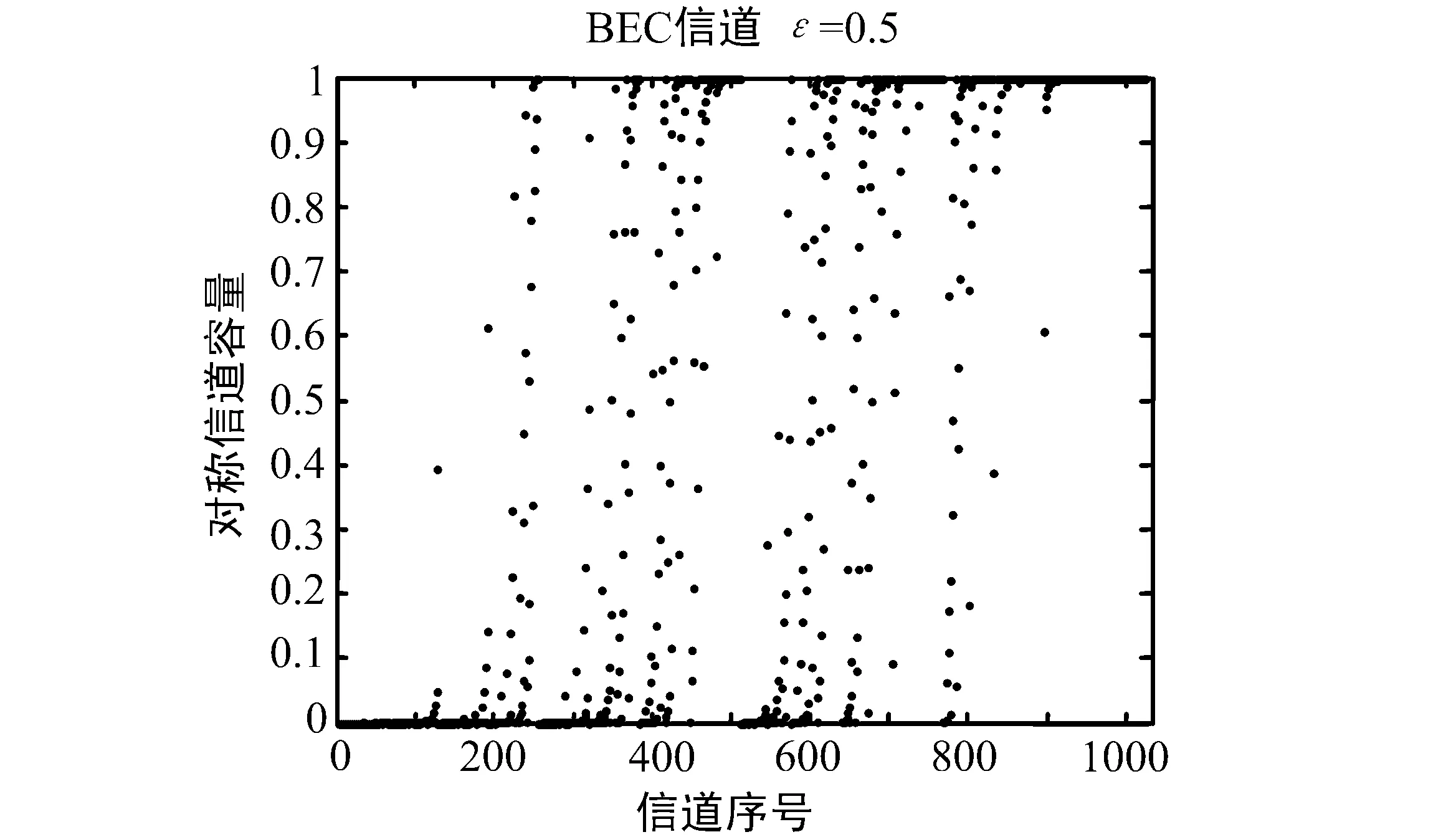
图5 信道极化后容量分布

在文献[8]中，Arikan提出了Polar码的逐次抵消(Successive Cancellation,SC)译码算法，但是在中短码长下译码效果不是很理想。因此，在SC译码算法的基础上，2011年Tal和Vardy、Chen和Niu分别提出了可以大大改善SC译码算法性能的列表译码算法[41-42]。

后来，为了进一步提高译码性能，又提出了CRC辅助的列表译码算法[43]，这是目前应用最广的Polar码译码算法。实际上，CRC辅助的Polar编码器可看作是一个串行级联编码系统，其中CRC码作为外码，Polar码作为内码。CRC的作用有两个方面：一是增加码的最小距离，从而改进高信噪比下的性能；二是帮助列表译码器选择正确路径。另外，还有众多其他学者做了许多尝试，如逐次抵消Stack译码等。

研究发现Polar码在多个方面都表现出优异的性能。目前，Polar码在编码调制、有记忆信道、窃听信道等方面的应用中也都展现出优异的性能。

除了上述介绍的几种逼近信道容量的编码外，还有一类应用广泛的面向数据包的编码：纠删码。它主要用来降低反馈与重传。Raptor类喷泉码被广泛用在广播与组播中，用来避免HARQ的反馈负担；在基于Aloha类协议的随机多址接入系统和点对点链路中，丢包以后，使用纠删码代替重传；另外，纠删码还被应用在CCSDS的近地卫星和深空通信中。

2.6 现代编码的应用

目前，能逼近信道容量的现代编码大多已经获得了实际的应用。在CCSDS的深空通信系统中，RS码和卷积码的级联一直是其标准中的一部分；如今，Turbo码和LDPC码也成为了其标准的一部分。CCSDS给出的Turbo码是由两个16状态递归卷积码并行级联而成的，编码器结构如图2所示,具体的码参数如表2所示。在表2中，同时给出了CCSDS建议的LDPC码的参数，这些LDPC码都具有准循环结构。

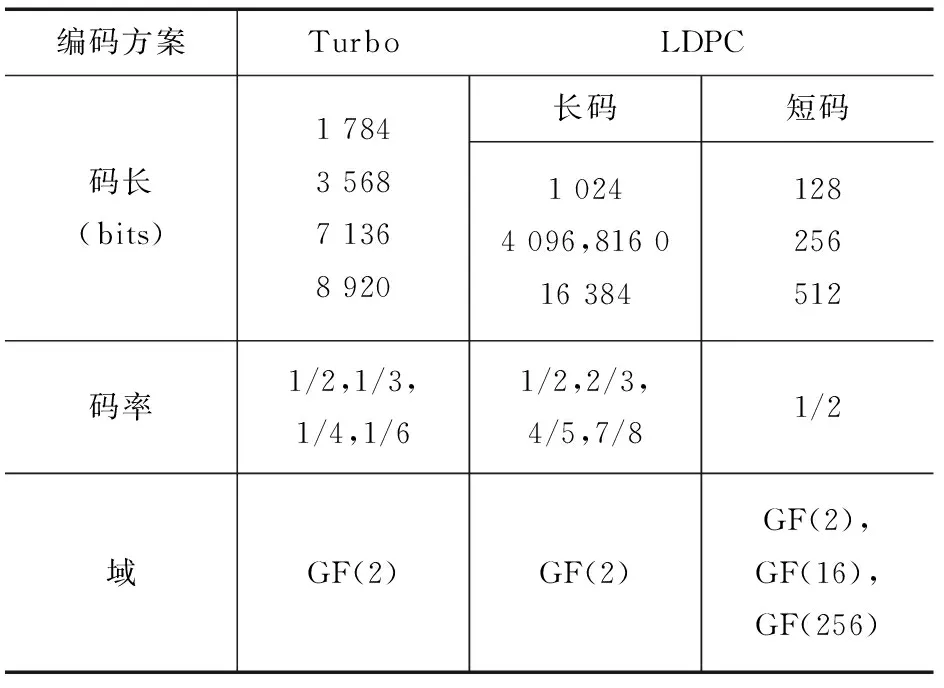
表2 CCSDS标准中Turbo和LDPC码参数

在下一代通信系统(5G)中，Turbo码、LDPC码、LDPC卷积码、Polar码都成为了强有力的候选者。5G通信系统主要定义了三类场景，分别是增强移动宽带业务(Enhanced Mobile Broadband，eMBB)、大规模机器通信(Massive Machine-type-communication,mMTC)和高可靠低时延通信业务(Ultra Reliable and Low Latency Communications,URLLC)；不同的场景具有不同的要求。eMBB场景要求支持更高的传输速率(峰值速率：上行链路达到10 Gbps，下行链路达到20 Gbps)、更高的谱效率(峰值谱效率：上行链路达到12 bps/Hz，下行链路达到30 bps/Hz)等；mMTC场景要求支持更大联接(每平方公里1×106个联接)，更低能耗(终端电池使用寿命达到15年)；uRLLC场景要求支持更低的延时(上下行链路0.5 ms，即端到端时延低于1 ms)，更高的可靠度(达到99.999 9%，即1ms内的误帧率低于10-6))，更低的错误平层等。从5G各个应用场景的关键性指标和现有信道编码技术的特点来看，采用原有4G中的信道编码技术方案已经难以满足5G的各种需求。目前Turbo码、LDPC码和Polar码都已经成为5G三个应用场景的热门候选方案。而对于mMTC和uRLLC场景来说，咬尾卷积码同样也成为了该场景的候选方案。表3和表4给出了其具体的候选方案。

表3 eMBB场景的候选编码方案

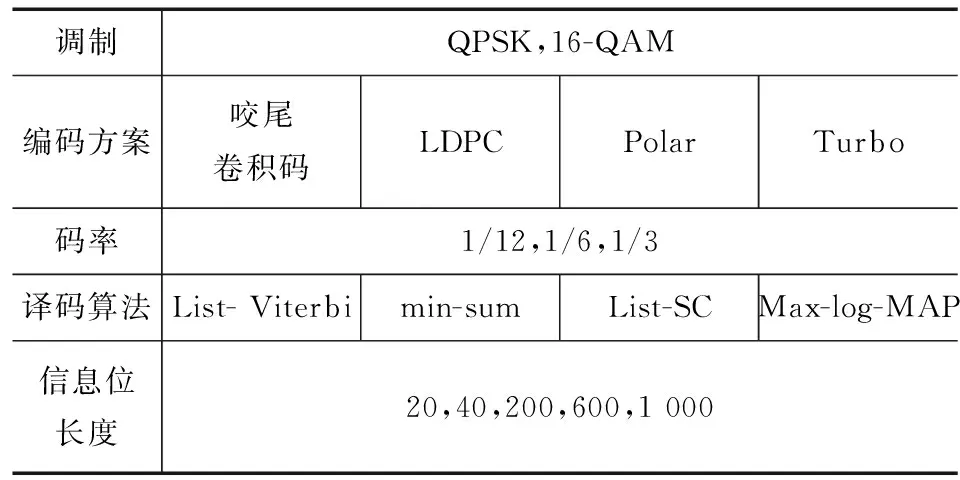
表4 mMTC和URLLC场景的候选编码方案

而在光通信系统中，最早使用的是经典信道编码如BCH码、RS码等；后来采用以它们为分量码构成的级联码；如今，LDPC码以及具有卷积结构的长码，如Staircase码也得到了广泛的应用。

另外，现代编码方案在其他一些系统也中得到了广泛应用如DVB和存储系统等。

3 结束语

从Shannon于1948年创立信息论算起，也已经过去了近70年了，人们在信道编码定理的指引下，一步步地从构造出比较接近信道容量的码到提出可逼近容量限的码，最后终于研究出能够达到容量限的实用编译码方法。本文重点介绍了几种能够逼近信道容量的现代编码：Turbo码、LDPC码、Polar码等；它们各具特点，各有应用场景：

① Turbo码：编码简单，适合于中短码长或FER要求不高的场景；② 二元LDPC码：译码简单，长码性能优异，错误平层低；③ 多元LDPC码：译码复杂度高，但中短码长下性能好，抗突发错误能力强，与高阶调制结合性能好，FER性能好，适合于突发短数据包的高可靠传输；④ 卷积LDPC码：长码下滑窗译码时延短，适合于连续流长数据包的低时延传输；⑤ Polar码：长码性能优异，短码性能好但其List译码复杂度高；⑥ 纠删码/喷泉码：数据包级的编码，可以用来代替HARQ。

目前，在时延非严格受限(允许码长充分长)的通信系统中，我们已经能够在简单的点对点信道上实现逼近容量限的信息传输。但是，在时延受限(有限长)的情况下，还需要继续寻找好码。

另外，在复杂信道环境以及网络通信情况下的信道容量，许多还是未知的，需要继续探索。

[1] Shannon C E.A Mathematical Theory of Communication[J].Bell System Technical Journal,1948,27(3):379-423.

[2] Hocquenghem A.Codes Correcteursd’erreurs[J].Chiffres,1959:147-156.

[3] Bose R C,Ray-Chaudhuri D K.On a Class of Error Correcting Binary Group Codes[J].Information and Control,1960,3(1):68-79.

[4] Reed I S,Solomon G.Polynomial Codes over Certain Finite Fields[J].Journal of the Society for Industrial and Applied Mathematics,1960,8(2):300-304.

[5] Elias P.Coding for Noisy Channels[J].IRE Convention Record,1955,4:37-47.

[6] Berrou C,Glavieux A,Thitimajshima P.Near Shannon Limit Error-Correcting Coding and Decoding:Turbo-Codes[C]∥ in Proceedings of IEEE International Conference on Communications (ICC).Geneva,1993:1064-1070.

[7] Gallager R.Low-Density Parity-Check Codes[J].IRE Transactions on Information Theory,1962,8(1):21-28.

[8] Arikan E.Channel Polarization:A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels[J].IEEE Transactions on Information Theory,2009,55(7):3051-3073.

[9] Hamming R W.Error Detecting and Error Correcting Codes[J].The Bell System Technical Journal,1950,23(2):147-160.

[10]Muller D E.Application of Boolean Algebra to Switching Circuit Design and to Error Detection[J].Transactions of the I.R.E.Professional Group on Electronic Computers,1954,EC-3(3):6-12.

[11]Lin S,Costello D J.Error Control Coding(Second Edition)[M].New York:Pearson Education,2004:194-270.

[12]Wozencraft J M,Reiffen B.Sequential Decoding[M].Cambridge:MIT Press,1961.

[13]Massey J L.Threshold Decoding[M].Cambridge:MIT Press,1963.

[14]Viterbi A.Error Bounds for Convolutional Codes and an Asymptotically Optimum Decoding Algorithm[J].IEEE Transactions on Information Theory,1967,13(2):260-269.

[15]Bahl L,Cocke J,Jelinek F,et al.Optimal Decoding of Linear Codes for Minimizing Symbol Error Rate[J].IEEE Transactions on Information Theory,1974,20(2):284-287.

[16]Elias P.Error-free Coding[J].Transactions of the IRE Professional Group on Information Theory,1954,4(4):29-37.

[17]Forney D.Concatenated Codes[M].Cambridge:MIT Press,1966.

[18]MacKay D J C,Neal R M.Near Shannon Limit Performance of Low Density Parity Check Codes[J].Electronics Letters,1996,32(18):1645-1646.

[19]Davey M C,MacKay J D.Low-Ddensity Parity Check Codes over GF(q)[J].IEEE Communications Letters,1998,2(6):165-167.

[20]Kudekar S,Richardson T J,Urbanke R L.Threshold Saturation via Spatial Coupling:Why Convolutional LDPC Ensembles Perform So Well over the BEC[J].IEEE Transactions on Information Theory,2011,57(2):803-834.

[21]Richardson T J,Shokrollahi M A,Urbanke R L.Design of Capacity-Approaching Irregular Low-Density Parity-Check Codes[J].IEEE Transactions on Information Theory,2001,47(2):619-637.

[22]Tanner R.A Recursive Approach to Low Complexity Codes[J].IEEE Transactions on Information Theory,1981,27(5):533-547.

[23]Ryan W E,Lin S.Channel Codes:Classic and Modern[M].New York:Cambridge University Press,2009.

[24]MacKay J D,Davey M C.Evaluation of Gallager Codes for Short Block Length and High Rate Applications[C]∥in Proceedings of IMA International Conference on Mathematics and Its Applications:Codes,Systems and Graphical Models.New-York,2000:113-130.

[25]Barnault L,Declercp D.Fast Decoding Algorithm for LDPC over GF(2q)[C]∥in Proceedings of Information Theory Workshop.Paris,2003:70-73.

[26]Declercq D,Fossorier M.Decoding Algorithms for Nonbinary LDPC Codes over GF(q)[J].IEEE Transactions on Communications,2007,55(4):633-643.

[27]Zhao D Y,Ma X,Chen C,et al.A Low Complexity Decoding Algorithm for Majority-Logic Decodable Nonbinary LDPC Codes[J].IEEE Communications Letters,2010,14(11):1062-1064.

[28]Chen C,Bai B M,Wang X P,et al.Nonbinary LDPC Codes Constructed Based on a Cyclic MDS Code and a Low-Complexity Nonbinary Message-Passing Decoding Algorithm[J].IEEE Communications Letters,2010,14(3):239-241.

[29]Chen C Y,Huang Q,Chao C C,et al.Two Low-Complexity Reliability-Based Message-Passing Algorithms for Decoding Non-Binary LDPC Codes[J].IEEE Transactions on Communications,2010,58(11):3140-3147.

[30]Huang Q,Zhang M,Wang Z L,et al.Bit-reliability Based Low-Complexity Decoding Algorithms for Non-binary LDPC Codes[J].IEEE Transactions on Communications,2014,62(12):4230-4240.

[31]Felstrom A J,Zigangirov K S.Time-varying Periodic Convolutional Codes with Low-Density Parity-Check Matrix[J].IEEE Transactions on Information Theory,1999,45(6):2181-2191.

[32]Costello D J,Dolecek L,Fuja T,et al.Spatially Coupled Sparse Codes on Graphs:Theory and Practice[J].IEEE Communications Magazine,2014,52(7):168-176.

[33]Lentmaier M,Sridharan A,Costello D J,et al.Iterative Decoding Threshold Analysis for LDPC Convolutional Codes[J].IEEE Transactions on Information Theory,2010,56(10):5271-5289.

[34]Kudekar S,Richardson T,Urbanke R.Spatially Coupled Ensembles Universally Achieve Capacity Under Belief Propagation[C]∥ in Proceedings of IEEE International Symposium on Information Theory(ISIT).Cambridge,2012:453-457.

[35]Smith B P,Farhood A,Hunt A,et al.Staircase Codes:FEC for 100 Gb/s OTN[J].Journal of Lightwave Technology,2012,30(1):110-117.

[36]Zhu M,Mitchell D G M,Lentmaier M,et al.Window Decoding of Braided Convolutional Codes[C]∥in Proceedings of IEEE Information Theory Workshop(ITW).Jeju,2015:143-147.

[37]Moloudi S,Lentmaier M,Amat A G.Spatially Coupled Turbo Codes[C]∥ in Proceedings of 8th International Symposium on Turbo Codes and Iterative Information Processing (ISTC).Bremen,2014:82-86.

[38]Huang K C,Mitchell D G M,Wei L,et al.Performance Comparison of LDPC Block and Spatially Coupled Codes Over GF(q)[J].IEEE Transactions on Communications,2015,63(3):592-604.

[39]Pusane A E,Feltstrom A J,Sridharan A,et al.Implementation Aspects of LDPC Convolutional Codes[J].IEEE Transactions on Communications,2008,56(7):1060-1069.

[40]Arikan E.Channel Polarization:A Method for Constructing Capacity-Achieving Codes[C]∥in Proceedings of IEEE International Symposium on Information Theory (ISIT).Toronto,2008:1173-1177.

[41]Tal I,Vardy A.List Decoding of Polar Codes[J].IEEE Transactions on Information Theory.2015,61(5):2213-2226.

[42]Chen K,Niu K,Lin J R.Improved Successive Cancellation Decoding of Polar Codes[J].IEEE Transactions on Communications,2013,61(8):3100-3107.

[43]Niu K,Chen K.CRC-Aided Decoding of Polar Codes[J].IEEE Communications Letters,2012,16(10):1668-1671.

Recent Progress in Channel Coding

BAI Bao-ming,SUN Cheng,CHEN Pei-yao,ZHANG ji

(State Key Laboratory of Integrated Services Networks,Xidian University,Xi’an Shaanxi 710071,China)

Channel coding is a key technique for reliable communication over noisy channels.This paper briefly introduces the development of channel coding and presents someimportant codes on the journey to channel capacity.Several capacity-approaching codessuch as Turbo codes,non-binary LDPC codes,LDPC convolutional codes and Polar codes are discussed.Then the characteristics of these codes and the applicationsofthese codesin deep-space communication,5G mobile communication and optical communication systemsare addressed.

channel coding;capacity-approaching;application;5G

10.3969/j.issn.1003-3114.2016.06.01

白宝明，孙 成，陈佩瑶，等.信道编码技术新进展[J].无线电通信技术,2016,42(6):01-08.

2016-07-27

国家973计划项目(2012CB316103)；国家自然科学基金项目(61372074)

TN911.22

A

1003-3114(2016)06-01-8

白宝明(1966—)，男，教授，博士生导师，西安电子科技大学通信与信息系统学科带头人、中国电子学会会士、电子学会信息论分会主任委员，主要从事信息与编码理论、编码调制技术、无线通信和量子通信方面的教学与科研工作。曾先后主持国家自然科学基金项目、国家863计划项目和国家科技重大专项课题的研究工作，获2012年度国家科技进步二等奖，在国内外刊物和学术会议上发表论文100余篇。