二次开发教材 拓展学生思维

江苏徐州市铜山区伊庄实验小学（221128） 赵 庭

二次开发教材 拓展学生思维

江苏徐州市铜山区伊庄实验小学（221128） 赵 庭

教师的教学内容要根据学情需要而定。对教材进行二次开发，可使教学素材更契合学生的认知水平，降低教学内容的难度，促进学生全面发展。

二次开发 思维能力 思维难度

二次开发教材是指根据实际教学需要，合理、科学地对教材进行扩充、删减、调整等优化处理，开发出适合学生学习的教学素材。

一、分层教学，降低思维难度

数学知识具有螺旋上升、环环相扣的特点。教材中的部分内容对学生来说难度很大，教师可以对教材内容进行二次开发，分层教学，实现新旧知识之间的有效过渡，降低学习的难度。

例如，“平均数”中有这样一道练习题：三名篮球运动员在6场比赛中的得分情况如下表（“——”表示没有上场比赛），那么谁的成绩最好呢？

?

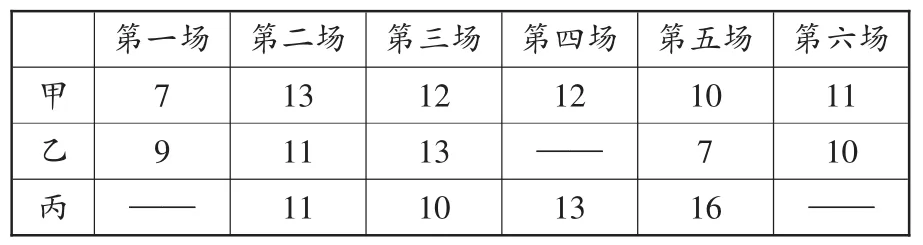
有的学生在思考这个问题时出现困难，无从下手，这是他们对平均数的含义理解不透彻的表现。这时，教师可以用分层教学的方法，引导学生将对这道题的思考分为三个层次：第一层次是求每名运动员的平均分，掌握求平均数的方法；第二层次是求三参加相同场数时的平均分，比如甲的4场比赛成绩分别是7、13、12、12，乙的4场比赛成绩分别是9、11、13、7，丙的4场比赛成绩分别是11、10、13、16，他们的平均分分别为11、10、12.5；第三层次是求三名运动员参加不同场数时的平均分，也就是题目所求。分层教学，可使学生明白用总分数除以总场数就能算出每名运动员的平均分，与参加场次是否相同无关。

这样的分层教学，拓宽了学生的思路，不仅让学生找到了解题思路，也让学生对平均数的意义和平均数在生活中的应用有了更深入的了解，提高了教学效果。

二、变“一”为“多”，丰富教学内容

变“一”为“多”包含两个层面，其一是一题多解，其二是一题多变。

一题多解是指对一道题进行深入挖掘，找出多种解法。例如，“简易方程”中的一道练习题：小红今年重36千克，比去年增加了2.5千克，小红去年的体重是多少千克？这道题目对于学生而言是非常简单的，利用在低年级时学习的方法就能根据“比去年少增加了2.5千克”直接列式求解：36－2.5＝33.5（千克）。但在这个阶段，学生的代数思维已经开始显现，教师可以引导他们用方程思想去解答这个问题：去年的体重＋2.5＝今年的体重或今年的体重－去年的体重＝2.5”，拓展学生的解题思维。

“一题多变”是在原题的基础上，开发出一系列与之相似或者相反的题目，把单一型的学习材料转变成综合型的学习素材。例如，“喝牛奶中的数学问题”中的一道题目：一杯牛奶，淘气喝了半杯后，觉得有点凉了，就去兑满了热水，然后又喝了半杯，请问淘气一共喝了多少杯牛奶，多少杯水？当学生解答出这个问题后，教师不妨改变条件，如把“又喝了半杯”改成“全部喝完”，让学生尝试回答改编后的问题。

教师对教学内容进行一题多解或一题多变的二次开发，不仅扩充了学习素材库，使得课堂更为丰满，还有效拓展了学生的思维，发展了学生举一反三的能力。

三、开放教学，促进思维灵活

教学中，教师可以适当对知识点进行延伸，开发出个性化的开放型学习材料。通过学习开放型知识，学生可以将零散的知识点联系起来，从而从宏观上把握方向，真正学会数学思考。

例如，教学“有余数的除法”后，我在课堂结束前给学生留下了一个开放性问题中的□里可以填哪些数字，使得商为2？首先，我让学生根据自己的经验猜一猜，然后再提示他们从被除数、除数、商和余数之间的关系出发去探究，即被除数＝除数×商＋余数，所以可以得到5□＝28×2＋余数。由于28×2＝56，那么被除数应该大于或等于56，且小于60，因此被除数可以是56、57、58、59，那么□里填6、7、8、9中的任何一个都能满足要求。

又如，教学“集合”后，我出示了一道开放性的题目：学校举行跳绳和跳高比赛，六（2）班参加跳绳比赛的有6人，参加跳高比赛的有4人，那么他们班一共有多少人参加了比赛？学生看完题目后纷纷说一共有10人参加了比赛，我质疑：“一定是10人吗？”教师的问题引起了学生的思考。结合本节课的知识点，学生意识到参加两个比赛的学生可能存在交叉的现象。顺着这个思路去思考，他们终于认识到参加比赛的人数可能是6人、7人、8人、9人或者10人。

通过增加开放性题目，学习素材库得到了扩充，学生的思维能力也得到了提高，增强了教学效果。

总而言之，二次开发教材是为了更好地开展教学活动，提高教学效果。教师对教材的二次开发要以学生的认知水平为基础，使教学素材更贴近学生的学习需求，从而使不同水平层次的学生都能有所进步和发展。

（责编 吴美玲）

G623.5

A

1007-9068（2016）35-043