基于COSMOS Motion的靶标传动机构选型分析

朱高贵，王德鑫，唐军军

(南京模拟技术研究所，江苏南京210016)



基于COSMOS Motion的靶标传动机构选型分析

朱高贵，王德鑫，唐军军

(南京模拟技术研究所，江苏南京210016)

基于SolidWorks软件平台的COSMOS Motion组件，对两种靶标传动机构设计方案进行运动仿真，得到两方案的运动机构的运行速率、力矩等随时间变化关系，从而直观判断方案的优劣，并确定该靶标系统的传动构型。该仿真方法可为其它相似传动结构的设计和选型提供借鉴。

靶标 COSMOS Motion 连杆机构 选型 仿真

0 引言

平面四杆机构以结构简单、构件数量少等优势在各类机械产品中广泛地应用[1-3]。但因各运动构件相互影响，常使机构产生的运行轨迹、传递的功率、扭矩等参数表达式复杂，计算、验证极其繁琐。在产品研发周期日趋紧张的形势下，要在极短时间内以传统的计算方法设计出一个满足性能要求、计算精确的四杆机构绝非易事。

典型靶标系统是以平面四杆机构作为控制靶板运动的执行机构。分别以曲柄摇杆机构和转动导杆机构两种型式的四杆机构作为某靶标系统执行机构的两种设计方案，需在两种方案中优选一种方案。使用SolidWorks软件建立两方案的理论模型，以CosMos Motion组件对两种方案进行运动仿真，得到的两种方案的四杆机构运行速率、力矩等变化规律，优选和确定该靶标系统的传动结构的设计方案，从而最大限度节约了分析计算的时间，缩短设计周期。

1 传动机构方案设计

在靶标内，四杆机构主要实现传递运动、牵引靶板在指定范围、一定时间内动作，如靶板的起倒、摇摆等等。按设计要求，实现该动作的主要结构方式是将靶板部件固结在从动件上，靶板在四杆机构运行平面上的投影通过从动件与机架的铰链轴，使靶板绕轴进行一定角度内的旋转。本文采取的四杆机构有两种方案，如图1所示，方案1为曲柄摇杆机构，方案2为转动导杆机构。在导杆机构中，导杆与滑块设计为丝杆-滑动螺母形式实现传动。在满足需求的条件下，需要对这两种机构的运行特性进行比较，分析各自的优势与缺点。

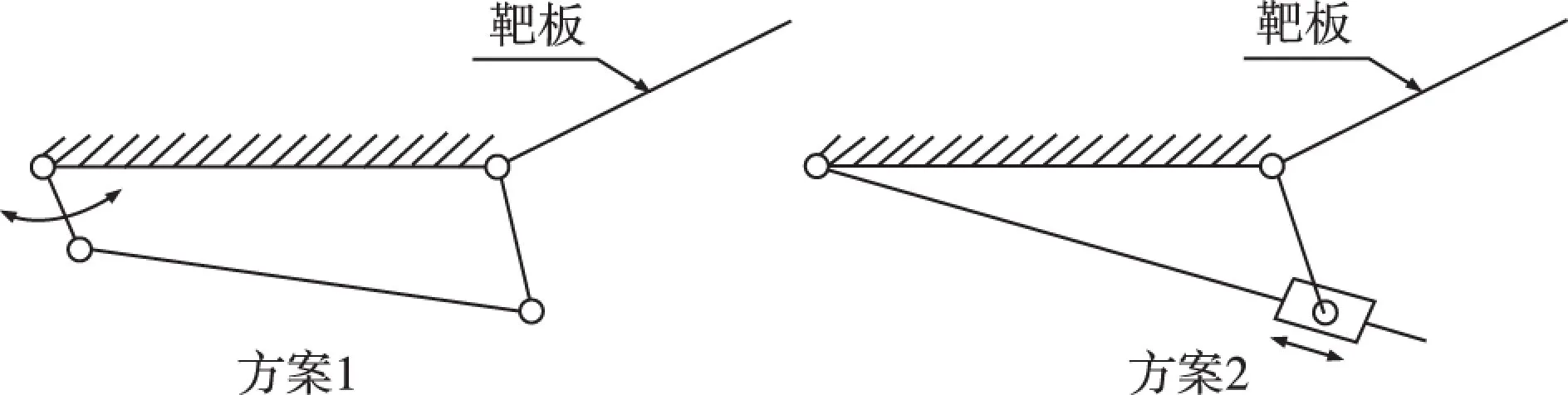
图1 靶标传动系统方案

靶标运动设计指标主要有：靶板从平放至竖起转动90°，运行时间不大于0.3 s，机构具有带动1 m左右高度铝制靶板的能力，该靶板质量约1.5 kg。

按以上要求，结合以往的靶板及靶板夹持机构的设计情况，估计整个靶板部件(包括靶板与夹持机构)质量会达到3.5 kg左右，而其平放时的重心在以转轴为原点255 mm的距离上。

图2 曲柄摇杆机构

以曲柄摇杆机构为例分析靶标传动机构运动特性。图2中杆1为主动件，以速度ω1转动。可通过图解法或解析法求得在任一位置(比如在杆1与杆4夹角为θ的位置)，杆3的角速度ω3，角加速度α3。根据刚体平面运动方程，杆3受到的力矩M=Jcα3，Jc为杆3及靶板部件的转动惯量，杆3受到的瞬时驱动功率P=Mω3。由于杆3的角速度和角加速度呈非线性，无论是通过图解法还是解析方法，要对机构运动全过程进行描述都是一件异常繁琐的工作，因而要进一步计算运动过程中的平均驱动功率等数据也非常困难。

2 建立理论模型与运动方式设定

为求得所述两方案的机构运动特性，利用COSMOS Motion组件进行运动仿真[5-8]，以期快速求得结果。

对图2所示曲柄摇杆机构，各杆长符合Ⅲ型机构，无急回特性[2,4]，以获得靶板组件起、倒行程时间相等；按靶板转动90°要求，杆1与杆3长度关系l3=1.414l1；l3初设为100 mm，l4设为320 mm。可以求出在极限位置该机构获得的最小传动角γ为44°～45°。

图3 转动导杆机构

对转动导杆机构也做类似编号(图3)。杆3长度l3设为100 mm，l4设为320 mm，杆3的左右极限位置与杆1夹角均为45°，以获得与曲柄摇杆机构基本相等的γ角。

在SolidWorks中启动COSMOS Motion组件，对上述两机构的运动方式进行设定。

对曲柄摇杆机构方案，软件将机架识别为静止零部件，杆1与杆4的铰接轴识别为第一个旋转副(Revolute)。设定运行环境，依次设定重力参数为Z轴负方向、仿真持续时间为0.6 s，即靶板组件完成一次起倒的时间。为第一个旋转副设定运动，即设定杆1的转速。按照杆3摆动90°时，杆1旋转半圈的关系，可知杆1速度为600°/s。

以上设定完成后，即可分别开始进行仿真，应注意开始时将靶板部件位置调整为平放的起始位置。

3 结果分析

图4和图5为靶板部件运动的角速度、角加速度以及驱动杆1旋转所需力矩三项参数合并成的曲线图。

图4 曲柄连杆机构运动特性图

对比两方案机构运行特性，主要有以下几点：

1)靶板部件的角加速度变化：曲柄摇杆机构-5 209～8 102°/s2，转动导杆机构为-3 292～2 076°/s2，运行过程中，在从动件(包括两机构中的杆3及靶板部件)尺寸、质量相同的情况下，前者的速度变化较大，因此靶板部件运动产生的惯性力较大，运行平稳性不及后者。在起或倒的瞬时，机构对靶板的冲击较大。

图5 转动导杆机构运动特性图

2)靶板部件的角速度变化：曲柄摇杆机构在靶板起、倒行程所用时间相等，即平均速度相等，但除正负号变化外，实际角速度曲线也不相同。在起行程中，速度变化更加不平均。

3)驱动力矩的变化：两套机构在旋转力矩(均为绿色)曲线上均有符号跳变的过程，显然，起始时力矩值的符号无论正负，都是使机构获得加速度的，即主动件(两机构中的杆1)功率输出的表现，正负符号只表示了COSMOS Motion组件对转矩方向的定义；而当力矩值越过零位变号时，理论上在主动件匀速转动状态下，从动件的运行受到阻碍，即表示此时靶板速度已获得最大值，主动件不再处于功率输出状态。在图4中0.2 s～0.3 s、0.4 s～0.6 s，图5中的0.2 s～0.3 s时间段均处于这种状态。在计算驱动功率时，可以不考虑该状态段。将力矩曲线数据输出后求出的均值(图6)，曲柄连杆机构为1 400 kgf·mm，即14 N·m，转动导杆机构为60 N·mm，即0.06 N·m。根据P=T·ω，可分别计算出两种机构运行全程的平均功率需求：

曲柄摇杆机构：P=T·ω=146.6 W

转动导杆机构：P=T·ω=44.4 W

另外，机构所需功率的瞬时值可由力矩曲线上的最大值求得，曲柄摇杆机构约200 W，转动导杆机构约240 W。

4 结论

1)从图6可以看出采用丝杆传动的转动导杆机构在运行平稳性、平均功率等特性上有一定优势。但因峰值功率较高，在设计时需考虑通过调整启动速度等手段进行调整，选择执行元件时也要根据功率平均值与峰值综合考虑。

图6 功率均值

2)机构的选型，除安全性能、尺寸、控制精确度以及成本等因素以外，运动特性的考察是非常重要的环节。通过仿真的方法，能够迅速获得以往数值计算方法很难求得的机构全程运动特性参数，精度也较高，能快速为机构的设计与选型提供重要的理论支撑。

[1] 丛爽，李泽湘．实用运动控制技术[M]．北京：电子工业出版社，2004．

[2] 郑文纬，吴克坚.机械原理:第七版[M].北京：高等教育出版社，1997.

[3] 吴宇泽，高志．机械设计[M]．北京：高等教育出版社，2009．

[4] 赵经文，王铎.理论力学:第五版[M].北京：高等教育出版社，1997.

[5] 张晋西，郭学琴.SolidWorks及COSMOS Motion机械仿真设计[M].北京：清华大学出版社，2001.

[6] 李大磊．SolidWorks 2009基础教程[M]．北京：北京邮电大学出版社,2009．

[7] 詹迪维．SolidWorks产品设计实例精解[M]．北京：机械工业出版社,2011．

[8] 张忠将．SolidWorks 2011机械设计完全实例教程[M]．北京：机械工业出版社,2011.

Selection of target transmission mechanism based on COSMOS Motion

ZHU Gaogui，WANG Dexin，TANG Junjun

The motion simulation of two kinds of design program on target driving mechanism was carried out, based on the COMOS Motion Componts of SolidWorks softaware platform. The variation of running speed and torque of the mechanism in the two schemes with time was obtained in the simulation, which could judgment schemes intuitively to determine the drive configuration of the target system. The simulation method can provide reference on the design and lectotype for other similar transmission mechanism.

target, COSMOS Motion, linkage mechanism, lectotype, simulation

TP391.9;E922.1

A

1002-6886(2016)06-0065-03

朱高贵，男，工程师，研究方向：机械设计、军训器材总体设计。

2016-08-29