基于ANSYS的齿轮根部裂痕故障诊断法*

王 龙，田怀谷，李 森，刘守法，董 锋

(1. 西京学院机械工程学院，陕西西安710123; 2. 西安热工研究院有限公司，陕西西安710032)



基于ANSYS的齿轮根部裂痕故障诊断法*

王 龙1，田怀谷1，李 森1，刘守法1，董 锋2

(1. 西京学院机械工程学院，陕西西安710123; 2. 西安热工研究院有限公司，陕西西安710032)

利用集总参数法建立了齿轮动力学模型，并以龙格-库塔数值法求解齿轮的振动响应。使用ANSYS 软件建立了无缺陷齿轮组与带齿根裂纹齿轮组模型，分析了两种齿轮组在多种转速下的振动特性。研究表明，齿根处裂纹对齿轮啮合刚度等效弹簧的振动频率影响不明显，且随着齿轮转速增大，带裂纹齿轮组振幅的均方根值略高于无缺陷齿轮组；带裂纹齿轮组在最大振幅附近产生边频现象，且齿轮转速越高边频越明显，此特征可用来判断齿轮组是否存在故障。

集总参数法 有限元分析 动态响应 等效弹簧

0 引言

齿轮广泛应用于工业机械、农业机械、航空航天和车辆的动力传输系统中，产生故障的形式有轮齿折断、疲劳点蚀和磨损等，这些故障会使齿轮产生周期性脉动力，在振动信号上体现为调制现象，在频谱图上会出现一系列的调制边频带[1-4]。振动的产生会使设备磨损严重、产生振动和噪音，造成严重经济损失，因此近年来齿轮动态特性一直都是工程领域的研究重点。

本文利用集总参数法和有限元法，对时域和频域内齿轮啮合振动特点进行了深入分析，讨论了齿根处有裂纹齿轮的振动特性，以期利用振动信号来判断齿根处是否出现裂纹。

1 动力学模型和运动方程

图1 齿轮系统数学模型

假设传动轴与轴承为刚性，利用集总参数法，使用等效质量、等效阻尼与啮合刚度等效弹簧的形式表达系统，忽略啮合点处的摩擦力与扭矩T1、T2的波动，所建模型如图1所示[5]，根据牛顿运动定律，由文献[6]得知齿轮1和2的系统运动方程式分别为：

(1)

(2)

其中I1、I2为齿轮的质量惯性矩，θ1、θ2为齿轮角位移，c为啮合阻尼系数，rb1、rb2为齿轮基圆半径，Kc(θ1)为啮合刚度，T1、T2为齿轮扭矩。

等效弹簧的位移为x=rb1θ1-rb2θ2，即为传递误差，将(1)与(2)组合可得等效弹簧的系统运动方程为：

(3)

表1 动力学模型各参数值

其中y1、y2、y3和y4的初始值由系统初始状态决定。

2 齿轮动态响应数值分析

齿轮为渐开线标准直齿圆柱齿轮，模数m=6 mm，齿数z1=23，z2=23，齿宽b=15 mm。在无缺陷齿轮的齿根处切出一条裂纹，裂纹的深度与齿宽比值为η=a/b，裂纹的位置系数β =vd/h(vd为裂纹与齿根圆距离，h为全齿高)，式中η = 0.1、β=0.11，生成的齿根处有裂纹齿轮模型如图2所示。齿轮使用的材料为钢，密度为7 850 kg/m3、杨氏模量为210 GPa、泊松比为0.3、材料屈服强度为250 MPa。

在ANSYS中设定齿面接触条件为无摩擦接触，接触力算法选择增广拉格朗日法，接触力Fc=knx+λ，其中kn为接触刚度，x为接触位移响应，λ为一外加的接触力变量，理想的接触是没有变形的，所以kn越大结果越精确，但收敛越慢。设定一齿轮轴孔为固定支撑，另一齿轮的轴孔为无摩擦支撑加扭矩100 N·m。

将几何模型划分成六面形状单元体，并在接触点附近划分加密网格如图3所示，加密区域网格尺寸设为0.2 mm。

图2 齿根处带裂纹的 图3 齿轮模型划分齿轮模型

2.1 啮合刚度等效弹簧的位移响应

给定齿轮一个初始转速，初始角位移为零，设定相对误差为10-4，时间步阶为10-4s，计算系统0～5 s的振动信号，截取系统稳态的振动信号。

取ζ =0.06，在不同转速下得到θ1和θ2的数值解，计算啮合刚度等效弹簧的位移响应x。齿轮旋转一周，则每对齿均啮合一次，则刚度变化呈周期性，所以在齿轮的振动成分中，存在啮合频率的成分。啮合频率的公式为fmesh=zω/60，图4为不同转速下位移响应x的时域图，可以发现啮合频率为45 Hz和90 Hz时振幅较大，啮合频率90 Hz时振幅最大。

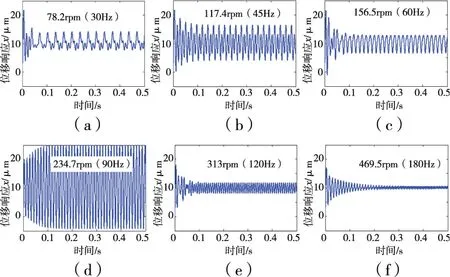
图4 无缺陷齿轮位移响应时域图

同样选取ζ =0.06，得到齿根带裂纹齿轮不同转速下啮合刚度等效弹簧的位移响应x的时域图，如图5所示，啮合频率为45 Hz和90 Hz时振幅较大，啮合频率90 Hz时振幅最大，与无缺陷齿轮相似。由于只有一个轮齿根部有裂纹，所以振动信号每经过23周期就出现一次较大的振幅。由此可见，无论齿轮有无缺陷，齿轮啮合频率接近啮合刚度等效弹簧固有频率或者固有频率的1/2时，等效弹簧的位移响应会很大，随着齿轮转速增大等效弹簧的位移响应迅速减小。因此齿轮的转速应该避免使啮合频率接近等效弹簧的固有频率或其半频，才能避免系统产生很大的振幅，齿轮工作时转速应远离这个区域。

科胡特曾说：“个体如果想要发展出健康、统合、连续的个体，关系背景是十分重要的；只有在这个关系中婴儿的自体客体需要通过养育者的情感协调得以满足，个体才有可能发展出健康的自我。也正是因为如此，如果养育者给予婴儿的反应并不协调，个体就有可能出现心理问题。”

图5 有缺陷齿轮位移响应时域图

2.2 振动特性对比分析

图6 等效弹簧位移的均方根曲线

获取振动达到稳态时的信号，截取3 s～5 s的时域信号，各转速下等效弹簧位移的均方根曲线如图6所示，可见转速为114.8 rpm(45 Hz)和227 rpm(90 Hz)对应的均方根处出现峰值，两种齿轮出现峰值的位置相同，但有裂纹齿轮组的均方根在很大范围内略大于无缺陷齿轮组，可见齿根裂纹会使齿轮啮合出现较大的振动。

2.3 有齿根缺陷齿轮振动频域分析

图7为带裂纹齿轮组在不同转速下的啮合频率频谱图，可见每个较大振幅旁均有边频出现，且齿轮转速越高边频越明显，边频的出现是由振幅调制现象引起的，振幅调制由数学原理解释为两种信号在时域上相乘相当于信号在频域上折积，若数值模拟的结果在频域啮合频率两侧出现边频，说明啮合频率为载波成分，齿轮转速频率为调制波成分。

随着齿轮转速增加，最大振幅先增大后迅速减小，齿轮转速227 rpm对应的最大振幅达到了14.69 μm，为所有情况下振幅最大值。

图7 有裂纹齿轮组的啮合频率频谱图

3 结论

1)无论齿轮有无齿根裂纹，齿轮啮合频率接近啮合刚度等效弹簧固有频率或者固有频率的1/2时，等效弹簧的位移响应均会增大，但随着齿轮转速提高，等效弹簧的位移响应迅速减小，可知使齿轮的啮合频率远离固有频率可避免共振产生。

3) 带齿根裂纹的齿轮组在最大振幅对应的频率附近出现边频现象，且齿轮转速越高边频越明显，此为带齿根裂纹的齿轮组的故障特征，这些都是无缺陷齿轮不具备的特征， 可依此来判断齿轮的齿根

处是否出现裂纹。

[1] 康传章，陈兵奎，张 靖，等. 齿轮系统振动信号的边频带研究及其应用[J]. 机械传动，2013，37(4): 41-43+76.

[2] Gosselin C M, Pereault L, Vailancourt C. Simulation and computeraided kinematics design of three-degreed-of freedom spherical parallel manipulators[J]. Journal of Robotic Systems, 1995, 12(12) : 857- 869.

[3] 刘辛军, 张立杰, 高 峰. 基于AutoCAD 平台的六自由度并联机器人位置工作空间的机械求解方法[J].机器人，2000，22(6)：457-464.

[4] 陈修龙, 赵永生. 并联机床运动仿真与运动学分析的新方法[J]. 中国机械工程, 2006, 17(5) : 467- 471.

[5] Kahraman A， Singh R．Non-linear dynamics of a geared rotor-bearing system with multiple clearances[J]．Journal of Sound and Vibration, 1991, 144(3)：469-506.

[6] Howard I, Jia S. The dynamic modeling of a spur gear in mesh including friction and crack[J]. Mechanical Systems and Signal Processing, 2001, 15(5):831-853.

Fault diagnosis method of gear root with rifts based on ANSYS

WANG Long, TIAN Huaigu, LI Sen, LIU Shoufa, DONG Feng

The dynamic model of the spur gear pair is built by lumped parameter method and the motion equations are solved by using Runge-Kutta method to acquire vibration response of the gear pair. The finite element model of defect-free gear pair and gear pair with root crack are established by ANSYS to analyze the vibration characteristics of the two gear pairs under conditions of different rotating speed. Results show that effects of the root crack on the vibration frequency of the meshing stiffness equivalent spring is not obvious. The RMS of the amplitude of gear pair with root crack is slightly higher than the defect-free gear pair as the speed increasing. There is side frequency in the vicinity of the maximum amplitude during meshing transmission of the gear pair with root crack, the higher the speed of the gear, the more obvious the side frequency, which can determine whether the gear pair has root crack.

lumped parameter method, finite element analysis, dynamic response, equivalent spring

TH132.413

A

1002-6886(2016)06-0048-04

陕西教育厅科学研究计划项目 (12JK1075)；西京学院教改项目(JGYB1616)。

王龙(1995- )，男，汉族，河南南阳人，校企合作试点培养学生。 刘守法(1980- )，男，汉族，河北沧州人，讲师，工学硕士，研究方向: 航空用有色合金FSW和 FSP技术及机床加工精度预测研究。

2016-06-20