超材料孔径成像雷达的辐射场自由度评价

吴振华，刘宏伟，张 磊，寇 娜

(1. 西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071; 2. 西安电子科技大学 信息感知协同创新中心，陕西 西安 710071; 3. 西安电子科技大学 天线与微波技术重点实验室，陕西 西安 710071)



超材料孔径成像雷达的辐射场自由度评价

吴振华1,2，刘宏伟1,2，张 磊1,2，寇 娜2,3

(1. 西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071; 2. 西安电子科技大学 信息感知协同创新中心，陕西 西安 710071; 3. 西安电子科技大学 天线与微波技术重点实验室，陕西 西安 710071)

针对目前尚无超材料孔径成像雷达辐射场评价体系的问题，提出使用辐射场测量矩阵列互相关系数的一阶和二阶统计量两个指标实现辐射场自由度评价的方法，并详细分析了超材料孔径成像雷达的重建性能．首先，分析了仅使用测量矩阵互相关系数均值评价指标的问题；然后，引入互相关系数方差指标来完善评价体系；最后，结合压缩感知理论，通过相变图在两个评价指标和成像重建精度之间建立了对应关系．仿真结果表明，所提方法可有效地对辐射场自由度进行评价，对超材料孔径成像雷达的设计具有指导作用．

超材料孔径成像雷达;自由度;互相关;压缩感知;相变图

当前雷达主动成像系统有两种主要的实现方式: 合成孔径成像[1]和实孔径成像．合成孔径成像原理是利用雷达与观测对象的相对运动来合成大尺寸的虚拟孔径，从而获得方位的高分辨能力．而实孔径成像是利用真实孔径天线产生很窄的波束来直接获得方位和俯仰的角分辨能力．一般来说，实孔径成像系统想要获得高的成像分辨率需要很大的天线孔径，而大天线孔径的实现往往需要庞大的天线阵列，这无疑使得成像系统的成本和系统规模大，实际应用难度大．

近几年出现的超材料实孔径成像系统[2-7]，是使用超材料孔径所辐射出来的辐射场对场景进行测量，结合压缩感知[8]来实现关联计算成像．超材料孔径天线类似于传统的漏波天线，在超材料表面随机分布着谐振频率在工作带宽内的不同谐振单元，在工作带宽内不同的工作频率下，每次产生谐振的谐振单元不尽相同，即随着激励源频率的改变，超材料孔径天线的发射方向图随之改变，实现了在操作带宽内通过频率扫描来获得许多不同的测量模式．该系统利用了超材料孔径的频率捷变特性，可以避免使用机械扫描和移相器，从而降低了成像系统的复杂度．文献[2]采用一维超材料孔径天线来实现对距离和方位的二维成像，系统在Ka波段 (17.5～ 26.5 GHz) 下发射包含101频点的扫频信号得到高度去相关的辐射场模式解，通过优化计算可获得 4 000 像素点的二维稀疏成像，系统成像帧率 10 Hz 实现动目标成像．该超材料孔径成像系统首次验证了超材料孔径微波关联成像的原理可行性，但该系统在超材料孔径设计和工作带宽选择上尚无完善的设计依据．文献[3]首先详细推导了在Ka波段 (17.5～ 26.5 GHz) 下超材料孔径天线关联成像的数学模型，定义平均互相关来评价测量矩阵的好坏，然后用偶极子模拟超材料谐振单元来验证二维超材料孔径天线对频率变化的敏感性，最后结合压缩感知重构算法实现了对俯仰、方位和距离三维前视场景的成像．文献[4]同样是在Ka波段 (17.5～ 26.5 GHz) 下，利用超材料孔径天线结合红外和光学传感器对前视场景实现全息计算成像．从原理上说，在保证测量能量的条件下，辐射场的空域自由度越丰富，最终的成像分辨力也会越强，这也是目前系统采用波形均是高波段大带宽的原因．虽然目前的原理系统和实验均证明了超材料孔径微波关联成像的可行性和优越性，但针对辐射场空间自由度尚未建立有效的评价体系，且辐射场自由度与成像重建性能之间的约束关系也并没有得到深入关注．从系统设计角度出发，亟需建立可以指导超材料孔径和波形设计的辐射场空间自由度评价体系，为超材料孔径天线提供可行的设计依据．

笔者在测量矩阵平均互相关的基础上引入互相关的方差指标来完善对辐射场自由度的评价，并通过对典型目标场景的微波凝视计算成像仿真实验来建立辐射场自由度与成像重建性能之间的约束关系．笔者首先将超材料孔径天线方向图进行等间隔采样来得到测量矩阵，然后量化表示出测量矩阵能够分辨对应场景单元的极限，在定义的成像质量评价标准下，通过仿真对比试验，来验证所提出的使用测量矩阵互相关的一阶、二阶统计量两个指标来评价辐射场自由度理论可行性，并且通过成像重建精度相变图[9]，在孔径设计与成像精度之间建立联系．

1 超材料孔径成像原理

超材料[10]是通过人工设计实现的具有超常微波电磁物理性质的复合结构或复合材料，通过在材料的关键物理尺度上的结构有序设计来获得超常的电磁物理特性，其本质是构建亚波长谐振结构来调控电偶极子和磁耦极子的极化特性，通过设计不同几何结构的亚波长基本谐振单元来调控产生不同的极化特性，从而产生不同的耦合电场或者磁场．超材料孔径天线由平行金属板微带线和基本谐振单元组成，基本谐振单元成条状分布在波导上面，输入不同频率的激励源，几何结构不同的电谐振单元在不同谐振频率产生谐振，将能量从波导辐射到自由空间．不同基本谐振单元的设计与分布会影响辐射场的特性，从而产生不同的方向图．

下面通过数学推导简单介绍超材料孔径微波成像原理．超材料孔径对电磁波进行调制形成空间散布的辐射场对场景目标进行照射，经目标反射的回波信号被接收天线接收，整个过程可通过一个线性测量方程表示．简便起见，这里使用一阶波恩近似散射模型[3]来描述此测量过程．假定辐射场为Ei，场景内目标散射形成的散射场为Esca，且有

其中，f(rs)表示目标的后向散射系数，用一阶散射模型对上式进行近似，上式可重写为

g(w)=∫ H(w，rs) f(rs)

其中，g(w)为天线接收的测量信号矢量，考虑超材料孔径天线固有的频率捷变性，使用测量矩阵H(w，rs)来表示辐射场，即

其中，Etx(w，rs)为天线工作在频率为w、距离rs处的辐射场大小，Erx(w，rs)为对应的散射场在距离rs处的大小．将场景目标离散划分为N个单元，超材料孔径成像雷达进行M个频点扫描测量，则式(2)重写成线性测量方程形式为

其中，gM是M×1维的接收测量信号，HM×N是 M×N 的测量矩阵，每一行对应着在不同工作频率下，经过采样后的天线方向图，fN为场景目标的后向散射系数，nM为 M×1 维的测量噪声项．

在测量方程式(4)条件下，对场景目标成像重建，可以认为是从观测值g恢复出场景目标后向散射系数f的过程．根据压缩感知理论，利用场景目标本身的稀疏性，可在有效测量模式情况下，使用l1稀疏重构优化将场景目标完整重构．稀疏约束的成像重建优化问题可描述为

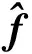
2 辐射场自由度

超材料孔径成像雷达的辐射场是由不同频率信号激励超材料孔径产生的，其具有高动态频率捷变特性，在成像过程中的作用等效于式(4)中的测量矩阵．根据压缩感知理论知识，测量矩阵需要满足较大的自由度，通常使用约束等距性(Restricted Isometry Property，RIP)描述，即便在噪声存在的情况下，使用重构算法依然可以以很高的概率将目标重构出来，需要说明，RIP特性是稀疏重建优化问题的充分条件，而非必要条件．针对超材料孔径成像雷达，测量矩阵对应的是频率捷变的辐射场，其纵向维度对应频率点数，横向对应成像空间网格数．对于有限带宽的超材料孔径微波成像测量矩阵而言，测量矩阵通常是横向维度比纵向维度高很多的扁矩阵，此时使用RIP作为评判辐射场自由度特性并不合适．另一种对测量矩阵进行评价的方法是分析列向量之间互相关特性，小的互相关系数通常能保证欠定测量下的有效稀疏重建精度，笔者将采用此思路进行工作．由式(2)可以看出辐射场是频率与空间的二维函数，定义空域相关函数来描述随机辐射场的随机统计特性，即

R(hk，hl)=

其中，hk和hl为测量矩阵不同的两列幅度方向图，由超材料孔径天线在成像场景内不同空间位置处进行频率扫描得到，·表示内积操作，(·)*为共轭转置运算．R为互相关函数．理想的随机辐射场满足如下的相关特性:

文献[11]定义了测量矩阵的列互相关平均值，描述为

图1 不同测量矩阵基列向量的互相关分布特性

图1(a)为随机测量矩阵，互相关系数幅值为1，是该列向量与其本身的互相关，不同列向量之间的互相关系数受彼此空间位置的差别影响不大，列向量之间的相关一致性较好．图1(b)为傅里叶基的情况，空间位置较近的时候互相关系数较高，距离较远时，互相关幅度值较低．图1(c)为某超材料孔径产生的辐射场形成的测量矩阵，不同位置之间的互相关系数一致性较差．在互相关系数有大的起伏时，对应基向量在重建过程中存在明显干扰，或有虚假目标出现，因此，单一均值并不能保证设计的完整性．笔者在考虑测量矩阵列互相关系数的均值基础之上，同时引入列互相关的二阶统计量来评价辐射场的自由度．在文中测量矩阵互相关的二阶统计量定义为

其中，Ri为测量矩阵中两两不同列向量之间的互相关值，m(m-1)/2表示列数为m测量矩阵H的列向量互相关值总个数，μg{H}为测量矩阵列向量互相关的均值．

在理想情况下，超材料孔径辐射场的互相关系数能够同时保持较小的均值和方差，这样既能保持整体重建性能，也能克服重建过程中引入的强虚假点．在设计实际超材料孔径成像雷达时，在预期成像精度的要求下，根据对应测量矩阵互相关的统计量值，来不断优化超材料孔径天线的设计，使其满足成像指标要求．下面通过仿真实验，来验证使用测量矩阵的一、二阶统计量来评价辐射场自由度的准确性．

3 仿真实验

下面进行超材料孔径雷达的成像设计实验，实验目的是建立对辐射场的有效评价体系，进而指导后续超材料孔径天线优化设计．文中所设计的超材料孔径天线采用印刷电路板(Printed Circuit Board，PCB)技术，属于漏波天线形式，阵面分布为CELC单元和耶路撒冷十字(Jerusalem)单元的0，1分布(0代表CELC单元，1代表耶路撒冷十字单元)，两种单元分别约占阵面的50%．天线尺寸为 250 mm× 250 mm，采用1分5的底馈形式，基板采用聚四氟乙烯板材，介电常数为2.65，损耗角正切为0.003，工作在 33～ 37 GHz 频段．

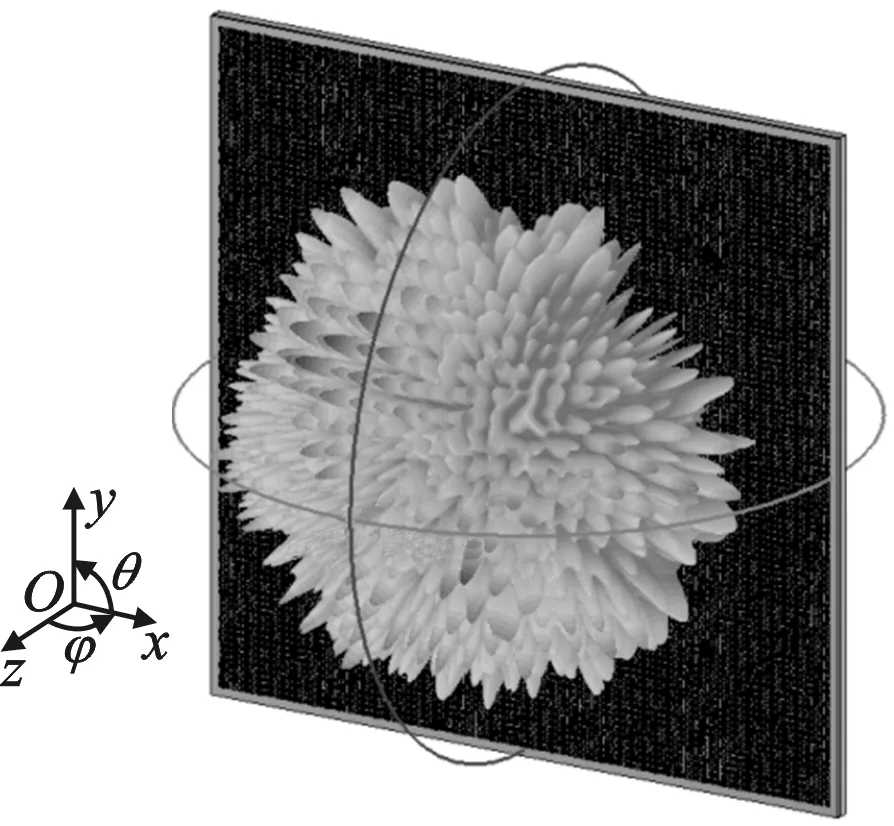
图2 全波仿真在35 GHz频率点处的辐射方向图

由于相邻谐振单元之间的互耦效应，想要对超材料孔径天线进行阵列计算分析来得到方向图变得非常困难，因此，采用全波分析的方法来得到天线的远场方向图．在中心频率 35 GHz 下，俯仰分辨率 Δθ= λcAx= 1.97°，方位分辨率 Δθ= λcAy= 1.97°，在工作带宽 33～ 37 GHz内，使用 25 MHz 间隔进行采样，产生161个频点．图2为 35GHz 时超材料孔径天线的三维方向图．

在进行仿真实验之前，首先需要确定所能恢复场景的有效像素单元大小，得出将场景划分的单元总数，通过不断增加俯仰与方位的采样间隔来观察设置目标恢复结果，最终确定俯仰与方位的维度均为26，实验的基矩阵维度为 161× 676．根据成像分辨率设计依据，汉字“十”目标具有一定的特殊性，设置原始目标为汉字“十”字，目标处的后向散射系数f幅值设为1，初相随机，没有目标处设置为0．

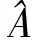
δ=

其中，N为每一组基的独立试验次数，计算N次试验相对重构误差的平均值．若恢复图像有虚假点或者遗漏点，则相对重构误差均能在数值上反映出来．为了观察测量基矩阵相关特性对成像性能的影响，需要使用对测量基矩阵相关特性敏感的数值优化算法．笔者使用的重构算法为文献[3]中使用的双步迭代收缩阈值算法(Two-step Iterative Shrinkage/Thresholding，TwIST)．TwIST算法是建立在迭代收缩阈值(Iterative Shrinkage/Thresholding，IST)稀疏重构求解算法基础之上的，其核心思想是在迭代求解过程中，利用前两步而非前一步的迭代值来更新当前迭代值，重构算法具有更快的收敛速度．

图3为原始目标和使用重构算法恢复出来的场景图像，场景均为超材料孔径成像雷达的前视区域．

图3 原始目标和使用重构算法恢复出来的场景图像

图3(b)中恢复图像对应的重建精度为0.733，相对重构误差为0.695．仅考虑测量矩阵列互相关的均值，观察重建精度和相对重构误差与互相关均值之间的关系，对每个测量矩阵进行50次蒙特卡洛实验．图4为重建精度和相对重构误差与测量矩阵互相关均值之间的关系图．

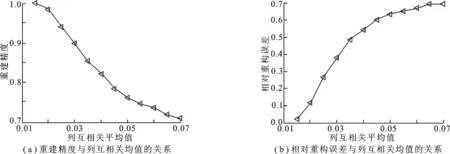
图4 重建精度和相对重构误差与测量矩阵列互相关平均值的关系图

从图4可以看出，随着测量矩阵列互相关均值的增大，重建精度会减小，相应的重构误差会增大，也即恢复的图像质量会降低，但成像质量的高低与测量矩阵列相关的均值之间并没有严格的线性关系，观察引入测量矩阵列互相关的方差值对实验结果的影响．图5为重建精度相变图与互相关均值和方差的对应关系．

在图5中，两条红线之外的数据不完整是因为在实验所用的测量基矩阵情况下，不同列相关均值和方差的范围不尽相同，因此，出现整个平面内未能铺满的情况．在均值很低时，方差的增大并不会明显降低重建精度，在均值增加到一定的固定值时，可以明显地看出重建精度会随方差的增大而减小; 在方差很低时，列互相关均值在较大的范围内可以保证重建精度，而方差较大时，能够保证重建精度的列互相关均值范围较窄．需要说明的是，在场景较为复杂时，得到的重建精度相变图同样表现为如图5所示的规律，提出的评价方法是可直接扩展到复杂场景的成像设计的．在实际设计过程中，可在预期重建精度的要求下，根据重建精度相变图得到对应的测量矩阵列互相关的一、二阶统计量值，通过不断的优化设计超材料孔径辐射场来满足测量矩阵的统计特性，成像重建精度相变图在超材料孔径设计与成像精度之间建立了对应关系．

4 结 束 语

超材料实孔径雷达作为一种新型的成像雷达，具有复杂度低，可以快速、实时成像的优点．针对辐射场自由度评价问题，笔者结合压缩感知理论，在测量矩阵互相关均值基础上，考虑引入测量矩阵互相关方差这一指标，并得出成像质量受测量矩阵列互相关的均值和方差共同影响的结论．通过仿真实验，验证了评价辐射场空间自由度指标的准确性，建立了辐射场自由度与成像重建性能之间的约束关系．

[1] 保铮, 邢孟道, 王彤. 雷达成像技术 [M]. 北京: 电子工业出版社, 2005.

[2]HUNT J, DRISCOLL T, MROZACK A, et al. Metamaterial Apertures for Computational Imaging [J]. Science, 2013, 339(6117): 310-313.

[3]LIPWORTH G, MROZACK A, HUNT J, et al. Metamaterial Apertures for Coherent Computational Imaging on the Physical Layer [J]. Journal of the Optical Society of America A, 2013, 30(8): 1603-1612.

[4]HUNT J, GOLLUB J, DRISCOLL T, et al. Metamaterial Microwave Holographic Imaging System [J]. Journal of the Optical Society of America A, 2014, 31(10): 2109-2119.

[5]LIPWORTH G, ROSE A, YURDUSEVEN O, et al. Comprehensive Simulation Platform for a Metamaterial Imaging System [J]. Applied Optics, 2015, 54(31): 9343-9353.

[6]YURDUSEVEN O, IMANI M F, ODABASI H, et al. Resolution of the Frequency Diverse Metamaterial Aperture Imager [J]. Progress in Electromagnetics Research, 2015, 150: 97-107.

[7]SLEASMAN T, IMANI M F, GOLLUB J N, et al. Dynamic Metamaterial Aperture for Microwave Imaging [J]. Applied Physics Letters, 2015, 107(20): 204104.

[8]DONOHO D L. Compressed Sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[9]ZHANG B C, HONG W, WU Y R. Sparse Microwave Imaging: Principles and Applications [J]. Science China Information Sciences, 2012, 55(8): 1722-1754.

[10]LAI A, ITOH T, CALOZ C. Composite Right/left-handed Transmission Line Metamaterials [J]. IEEE Microwave Magazine, 2004, 5(3): 34-50.

[11]DUARTE-CARVAJALINO J M, SAPIRO G. Learning to Sense Sparse Signals: Simultaneous Sensing Matrix and Sparsifying Dictionary Optimization [J]. IEEE Transactions on Image Processing, 2009, 18(7): 1395-1408.

(编辑：李恩科)

Degree of freedom evaluation in the radiation field for metamaterial aperture imaging radar

WUZhenhua1,2，LIUHongwei1,2，ZHANGLei1,2，KOUNa2,3

(1. National Key Lab. of Radar Signal Processing, Xidian Univ., Xi’an 710071, China; 2. Collaborative Innovation Center of Information Sensing and Understanding, Xidian Univ., Xi’an 710071, China; 3. Science and Technology on Antennas and Microwave Lab., Xidian Univ., Xi’an 710071, China)

There has no complete evaluation system to measure the radiation field of metamaterial imaging radar currently. This paper presents a method of using the first and second cross-correlation statistics of the measurement matrix to assess the degree of freedom of the radiation field, and the reconstruction performance of metamaterial imaging radar is analyzed based on the method. The inaccuracy caused by using only the mean value of measurement matrix cross-correlation is analyzed first. Then the cross-correlation coefficient variance indicator is introduced to develop a new evaluation system. Finally, combined with the compressed sensing theory, the corresponding relationship between imaging reconstruction precision and the two indicators is established through the phase diagram. Simulation results show that our method effectively evaluates the degree of freedom of the radiation field and guides the design of metamaterial imaging radar.

metamaterial aperture imaging radar; degree of freedom; cross-correlation; compressed sensing;phase diagram

2015-11-10

时间：2016-04-01

国家杰出青年科学基金资助项目(61525105)；国家自然科学基金资助项目(61271291，61201285，61301280)；新世纪优秀人才支持计划资助项目(NCET-09-0630)；全国优秀博士学位论文作者专项资金资助项目(FANEDD-201156)；中央高校基本科研业务费专项资金资助项目

吴振华(1993-)，男，西安电子科技大学博士研究生，E-mail:wudoufenglan@gmail.com．

http://www.cnki.net/kcms/detail/61.1076.tn.20160401.1622.014.html

10.3969/j.issn.1001-2400.2016.06.007

TN957.52

A

1001-2400(2016)06-0039-06