基于可信性理论的Mean-CVaR投资组合优化
李 淼,胡永宏
(1.北京市工商行政管理局 东城分局,北京 100007;2.中央财经大学 统计与数学学院,北京 100081)
【统计理论与方法】
基于可信性理论的Mean-CVaR投资组合优化
李 淼1,胡永宏2
(1.北京市工商行政管理局 东城分局,北京 100007;2.中央财经大学 统计与数学学院,北京 100081)
选取CVaR作为风险度量指标,在可信性理论的基础上构建Mean-CVaR投资组合模型,采用Markov过程预测作为模糊变量的预期投资收益率,并设计基于模糊模拟和遗传算法的混合智能算法以求解;选取上证50成份股2013—2014年的日度历史交易数据,将该模型应用到中国证券市场,结果发现该投资组合模型与中国证券市场的环境具有一定的适应性,能够为投资者的投资决策提供依据。
可信性理论;Mean-CVaR;混合智能算法
一、引 言
1952年Markowitz首次提出了均值-方差投资组合模型,该模型将方差作为风险度量的指标,开启了现代投资组合理论的大门[1]。此后,针对方差度量风险所存在的缺陷,Bawa、Konno、Rockafellar和Uryasev等先后提出了下偏矩、绝对偏差、VaR和CVaR等风险度量指标[2-4],CVaR是超过VaR部分的风险损失值,满足一致性风险度量的性质,具有良好的统计性质,也更符合对风险的预期。
传统投资组合理论的研究大多从概率论和线性规划理论出发,只考虑了证券市场的随机不确定性,而忽略了证券市场的另一种非常重要的不确定性表现形式——模糊性。1965年Zadeh提出了模糊集合的概念,创建了模糊数学理论;Liu定义了可信性测度,创建了可信性理论。此后,对投资组合的研究开始加入了对不确定性因素的考量,改进了Markowit衡量期望收益率的弊端。Tanaka、Huang、Qin等分别从模糊理论、可信性理论出发对收益率进行描述,并基于此构造投资组合模型,分别采用正交化、主成分分析法和混合智能算法对模型求解[5-7]。
针对以上两方面,中国学者也进行了研究,牛昂、姚刚对VaR的计算方法进行了介绍[8-9];荣喜民等研究了均值-VaR的有效前沿[10];林旭东等研究了均值-CVaR的有效前沿[11];庄新路、高振斌等将收益率描述为模糊变量,并建立投资组合模型,得出模糊环境下的投资组合模型能更好符合投资者主观愿望的结论[12-13]。
综上所述,对投资组合理论的研究主要是围绕风险和收益两个方面进行的,目前还没有学者对在可信性理论下综合考虑CVaR风险及市场双重不确定性的投资组合模型进行实证研究。因此,本文在构建投资组合模型时,综合考虑证券市场的双重不确定性,将收益率描述为随机模糊变量,采用CVaR作为风险度量指标,构建基于可信性理论的投资组合模型,利用模糊模拟和遗传算法的混合智能算法对模型进行求解,并利用上证50指数的50支成份股进行实证分析。
二、可信性理论基本概念
在对事件进行决策的过程中,为保证决策结果的准确性,需综合考虑事件的随机性和模糊性。1965年Zadeh最早对模糊集合的概念进行了阐述,建立了隶属函数,通过该函数较为精确地刻画出元素与集合之间的关系,并基于此创建了模糊集合理论。为了更详细地阐述随机性和模糊性之间的本质区别,Zadeh于1978年又进一步提出了可能性理论,而由于可能性测度缺少自对偶性会导致极端的可能性,Liu于2002年提出了可信性测度的概念,从而创建了可信性理论。下面对模糊集合理论、可能性理论和可信性理论的基本概念进行简单介绍。

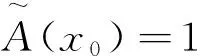
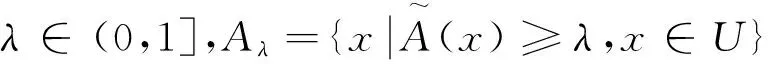

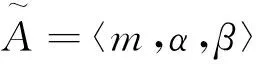
定义4 设Θ是一个非空集合,该集合存在幂集P,若集函数Pos满足如下定理:
公理1 Pos{Θ}=1。
公理2 Pos{φ}=0。
则Pos称为Θ的可能性测度,三元组(Θ,P,Pos)为可能性空间。
由于可能性测度缺少自对偶性,会导致极端可能性的出现,可信性测度使这一问题得到了改善。
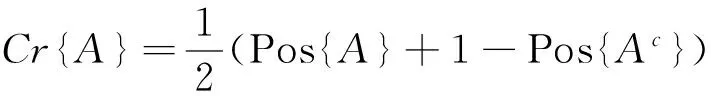
此外,可信性测度Cr满足以下四条公理:
公理1 规范性:Cr{Θ}=1。
公理2 单调性:如果A⊂B,那么Cr{A}≤Cr{B}。
公理3 自对偶性:有Cr{A}+Cr{Ac}=1,其中A表示任意事件。
则Cr{A}称为事件A的可信性测度,三元组(Θ,P,Cr)称为可信性空间。
基于可信性理论,给出模糊变量及其基本特征的概念:
定义6 令可信性空间为(Θ,P,Cr),存在一个可测函数,使该空间可以通过实数集一一表示出来,则这个可测函数就称为模糊变量。

定义8 模糊变量ξ的期望值为:
定义9 设ξ为一个模糊变量,e为该模糊变量的一个有限期望值,则模糊变量ξ的方差为:V[ξ]=E[(ξ-e)2] 。
三、基于可信性理论的Mean-CVaR投资组合模型
(一)模型的构建
模糊CVaR是指模糊风险资产在一定置信水平条件下未来一段时间可能遭受的超过VaR值的损失平均值,是对超过VaR值的可能遭受的潜在平均损失的测度,其数学定义为:
模糊CVaR满足一致性风险测度的四条性质,即平移不变性、单调性、正齐次性、独立次可加性,因此模糊CVaR风险测度属于一致性模糊风险测度。
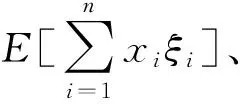


可得投资组合的模糊CVaR风险为:

其中[f(x,ξ)-ξVaR(α)]+=max{f(x,ξ)-ξVaR(α),0}
综上,基于模糊CVaR风险指标的投资组合模型有如下两种形式:
第一,保证收益水平且风险值最小。
(1)
其中r是收益标准,α是给定的置信水平。
第二,维持风险水平且收益最高。
(2)
其中δ是给定的风险标准,α是给定的置信水平。
(二)混合智能算法
由上述投资组合模型知,每种资产计算求得的三角模糊数是模型的输入数据,使模型具有模糊性的目标函数和约束条件,而一般的线性规划方法无法求解具有模糊性的投资组合模型,这时就需采用模糊模拟方法求解目标函数和约束条件;同时,为了找到满足条件的最优解,还需采用遗传算法来寻求全局最优解,所以本文基于上述两种算法,设计出混合智能算法对模型进行求解。
1.模糊模拟
当投资组合收益率为模糊变量且无法准确求出其期望值等时,可通过计算机程序近似求解其值,这样的方法就是模糊模拟。下面对模糊变量的期望、CVaR的模糊模拟方法进行介绍:
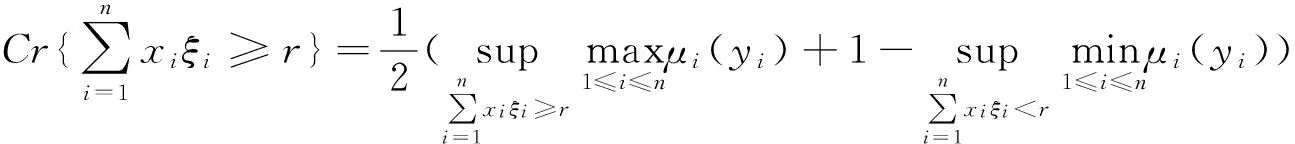
步骤1:设m=1,M是给定的正整数。
步骤2:随机生成n个实数wim,i=1,2,…,n。

步骤4:如果m>M,则继续;若m≤M,令m=m+1,返回步骤2。
(2)模糊模拟计算期望值。模糊变量的期望值可由模糊期望的定义式进行模糊模拟求得,即:
步骤1:令e1=0、e2=0、j=0、h=M/N,其中M是一个充分大的非负实数,N是一个充分大的正整数。
步骤2:把[0,M]和[-M,0]分别划分成N个区间[zj,zj+1]和[zj',zj+1'],其中zj=jh、z'j=-M+jh、j=0,1,…,N-1。

步骤4:如果j=N,该过程结束,返回e1-e2的值,即为模糊期望值;若j (3)模糊模拟计算VaR风险测度。当不等式Cr{∑xiξi≤r}≥α时,所求得的最小r值,即为模糊VaR风险测度,先令: 步骤1:设k=1,同时设定一个充分大的正整数N。 步骤2:随机生成n个实数wim,i=1,2,…,n。 步骤4:如果k>K,则继续;若k≤K,令k=k+1,返回步骤2。 步骤5:寻找满足L(r)≥α的最小的r值。 步骤6:返回r。 (4)模糊模拟计算CVaR风险测度。基于模糊VaR风险测度的模糊模拟步骤,可得到模糊CVaR风险测度的模糊模拟的具体算法: 步骤1:置e=0。 步骤3:找到满足L(ri)≥αi的最小值ri。 步骤4:置e=e+riαi。 步骤5:重复执行上述步骤2~5,共执行N次。 2.遗传算法 遗传算法借鉴了生物界的进化规律,对自然化过程进行一系列模拟,从而达到找到最优解的目的,这种方法能够有效解决复杂的全局优化问题。此外,对于所要优化的问题来说,遗传算法对数学性质的限制和要求较少,这都使得遗传算法具备极强的适应性。使用遗传算法求解优化问题一般需要通过以下几个操作步骤来完成:染色体的表示结构、处理约束条件、初始化过程、评价函数、选择、交叉和变异等。 处理约束条件:检验所生成染色体是否符合模型中约束函数的条件,若符合则保留,否则重新生成。 初始化过程:对随机生成的染色体进行约束判定,符合则保留并继续产生下一条染色体,否则再随机选择,直到产生事先设定的初始种群数pop-size。 交叉和变异操作:对染色体进行交叉和变异操作,目的是对父代染色体进行更新替代,从而生成更优的染色体组合。 3.混合智能算法 步骤1:随机产生pop-size个染色体,通过模糊模拟方法对所生成的染色体进行判定,直到生成pop-size个符合条件的染色体。 步骤2:通过模糊模拟的方法,对步骤1中最终产生的染色体进行求解,分别求得每个染色体的目标函数值,并根据计算结果对染色体进行排序。 步骤3:根据给定的评价函数,计算出每个染色体的适应度。 步骤4:通过轮盘赌轮技术对染色体进行选择。 步骤5:通过交叉和变异操作,对父代染色体进行更新换代,以获得新的可行染色体。 步骤6:重复步骤2~5,直到定义的次数为止。 步骤7:基于上述过程返回最优解。 考虑到证券市场的特点以及马尔可夫过程的特性,可以将证券市场不同期限的收益率看作是一个马尔可夫链,因此可以采用马尔可夫过程预测资产收益率。同时,由于证券市场的模糊不确定性的存在,将资产收益率描述为模糊变量,并用三角模糊集来刻画,具体预测方法如下: 步骤1:计算资产的历史收益率。根据历史交易数据中资产的开盘价、最低价、最高价和收盘价,计算出第i支股票在第t时刻最高价、最低价和收盘价的收益率的值,具体计算方法为: 根据上述公式显然可得到rit高≥rit收≥rit低。 步骤2:将历史收益率数据ritk(其中k=高、收、低)的取值区间作为收益率的分布状况,分别计算出第i支股票最高价、最低价和收盘价收益率在全部时刻的最大值、最小值,并将其分别定义为取值区间的上限和下限,根据上下界限将其等分为N个区间,记为状态1至状态N。 步骤4:建立线性方程组。求得证券投资收益率处于状态区间1,2,…,N的概率: 设上述方程组的唯一解为: 从而求得证券投资收益率处于区间1,2,…,N的概率分别为P1,P2,…,PN。 (一)样本选择与参数设定 本文选取上证50指数所包含的50支成份股2013年1月1日至2015年1月16日的历史交易日度数据(所选数据均来自于国泰安数据库),并基于可信性理论的Mean-CVaR投资组合模型(1)进行实证分析。首先对该模型构建其求解过程中所涉及的参数进行设定,见表1。 表1 参数设置表 其中区间数N表示将收益率的状态空间数量设置为3;最低收益率是50支股票期望收益率的平均值,表示的是模型(1)中的r值。此外,可以看到最低收益率的值为负数,在实际的投资过程中应该考虑更高的期望下限,但本文在研究的过程中完全从历史数据的角度出发,意在考察依照历史数据通过该模型进行投资的效果;表1中其他参数为混合智能算法求解过程中的相应数值。 (二)Mean-CVaR投资组合模型的静态实证 选取2013年1月1日到2014年12月31日的历史交易数据,通过C程序运用Markov过程预测出2015年1月5日全部50支股票的三角模糊收益率,具体结果见表2。 将得到的三角模糊收益率作为输入变量输入到Mean-CVaR投资组合模型中, 通过C程序运行混 表2 三角模糊收益率预测值及最优投资比例表 合智能算法的求解过程,最终得到最优的投资组合比例,所得结果同见表2。 通过上述结果,可以得到下一期的预期投资组合收益率为3.5%。 (三)Mean-CVaR投资组合模型的动态实证 为了验证Mean-CVaR投资组合模型在中国证券市场的适应性,选取2013年1月1日到2015年1月16日的历史交易数据,按照上述过程计算出连续10个交易日的预期投资组合收益率,并将得到的预期投资组合收益率与上证50指数的实际收益率值进行对比,具体结果见表3。 表3 投资组合与上证50指数收益率表 根据表3的计算结果,基于可信性理论构建的Mean-CVaR投资组合模型得到的投资组合收益率有7天要高于上证50指数的实际收益率,说明在中国证券市场环境下该模型的应用具有较强的实用性和有效性,该方法能够为投资者提供适应市场环境的投资策略。 本文综合考虑投资者对于风险和收益的双重需求,构建了基于可信性理论Mean-CVaR投资组合模型,并从静态和动态两个方面对投资组合模型进行了实证分析,结果表明该模型在中国证券市场环境下的应用具有较强的实用性,能够为投资者提供有效的投资策略,是投资组合理论在中国证券市场应用的一次有益尝试。 [1] Markowitz H. Portfolio Selection [J].Journal of Finance,1952,7(1). [2] Bawa T S. Optimal Rules for Ordering Uncertain Prospects[J]. Journal of Financial Economics,1975(10). [3] Konno H. Piecewise Linear Risk Function and Portfolio Optimization[J]. Journal of the Operations Research Society of Japan,1990,133(2). [4] Rockafellar R T, Uryasev S. Optimization of Conditional Value-at-Risk[J]. Journal of Risk,2000(2). [5] Tanaka H,Guo P,Turksen I B.Portfolio Selection Based on Fuzzy Probabilities and Possibility Distributions[J]. Fuzzy Sets and Systems . 2000(111). [6] Huang X X. Fuzzy Chance-Constrained Portfolio Selection[J]. Applied Mathematics and Computation,2006(177). [7] Qin Z, Li X , Ji X. Portfolio Selection Based on Fuzzy Cross-entropy[J]. Journal of Computational and Applied Mathematics,2009,228(1). [8] 牛昂.银行风险管理的新方法[J].国际金融研究,1997(4). [9] 姚刚.风险值测定法浅析[J].经济科学,1998(1). [10]荣喜民,武丹丹,张奎廷.基于均值-VaR的投资组合优化[J].数理统计与管理,2005(5). [11]林旭东,巩前锦.正态条件下均值-CVaR有效前沿的研究[J].管理科学,2004(3). [12]庄新路,庄新田,黄小原.基于VaR风险指标的投资组合模糊优化[J].数学的实践与认识,2003(3). [13]高振斌.基于可能度的模糊证券投资组合优化模型[J].统计与信息论坛,2015(5). (责任编辑:郭诗梦) 感谢审稿专家 尊敬的审稿专家: 各位好! 一份好的学术期刊是主办单位、编委、审稿专家、编辑、作者、读者精诚合作、齐心协力、共同努力的结晶。学术质量与水平是期刊的生命之根,质量的好坏、水平的高低,关键在于审稿专家的工作质量。长期以来,你们以严谨的治学态度和无私的奉献精神,为《统计与信息论坛》鼓实劲、出实力,默默付出了许多心血和劳动,为《统计与信息论坛》的发展做出了巨大贡献。因为有你们保驾护航,《统计与信息论坛》由无名小草成长为参天大树,跻身于中国优秀学术期刊行列。在此,向各位专家表示崇高的敬意和衷心的感谢! 秋叶落去,春芽复生,新的年轮又将启动。恭祝各位审稿专家在新的一年里身体健康,工作顺利,阖家幸福!新的一年里,在你们的继续帮助支持下,我们将更加努力,不断提高期刊学术水平和服务质量,把《统计与信息论坛》办得更好,为统计学的发展做出更大贡献。 《统计与信息论坛》编辑部 Portfolio Optimization of Mean-CVaR Based on Credibility Theory LI Miao1,HU Yong-hong2 (1.Dongcheng Branch, Beijing Administration for Industry and Commerce,Beijing 100007, China;2.School of Statistics and Mathematics, Central University of Finance and Economics, Beijing 100081, China) Constructing Mean-CVaR portfolio model based on credibility theory, the CVaR is chosen as the risk measurement index and according to the Markov process to predict fuzzy profit rate and designed a hybrid intelligent algorithm based on fuzzy simulation and genetic algorithm to solve. It makes the model to apply to the stock market in China selected SSE 50 constituent stocks of 2013-2014 years of historical transaction data. The result shows that the model of portfolio investment has certain adaptability with the stock market in China and can provide the basis for the investment decisions of investors. credibility theory;Mean-CVaR;hybrid intelligent algorithm 2016-08-18;修复日期:2016-10-15 国家自然科学基金面上项目《稳健投资组合选择的并行最优化算法研究与实现》(61272193) 李 淼,女,辽宁锦州人,经济学硕士,研究方向:金融统计分析; 胡永宏,男,陕西韩城人,管理学博士,教授,博士生导师,研究方向:金融计量分析,综合评价方法与应用。 F830.9∶O211.62 A 1007-3116(2016)12-0023-07

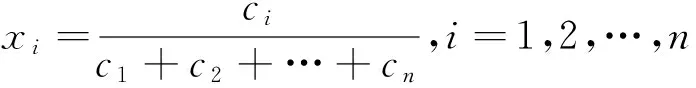

四、基于马尔可夫过程的模糊收益率预测方法

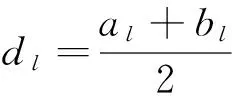

五、实证分析



六、总 结

