统计显著性:一个被误读的P值——基于美国统计学会的声明
郝 丽,刘乐平,申亚飞
(天津财经大学 大数据统计分析中心,天津 300222)
【统计理论与方法】
统计显著性:一个被误读的P值
——基于美国统计学会的声明
郝 丽,刘乐平,申亚飞
(天津财经大学 大数据统计分析中心,天津 300222)
美国统计学会“关于统计显著性与P值”的官方声明发布之后,再次引发国内外研究学者对P值的广泛关注。在介绍国内统计教材中假设检验的基本内容和步骤的基础上,以“硬币投掷”与“背影识人”为例直观性解释P值、统计显著性与统计功效等相关概念,并引用心理学统计经典调查案例分析P值被误读的原因。同时,基于美国统计学会的声明,给出正确使用P值的建议。
统计显著性;P值;心理统计学;贝叶斯统计
一、引 言
2014年2月,在美国统计学会(ASA)召开的一次重要学术论坛上,来自美国曼荷莲女子学院(Mount Holyoke College)的数学和统计学荣誉退休教授George Cobb,以一问一答的方式提出了如下有趣的问题:“为什么那么多大学和研究院都在教P=0.05?因为那是科学社团和期刊编辑仍然都在用的标准”;“为什么还有那么多人在用P=0.05?因为大学和研究院里还在这么教”。
Cobb教授关切的问题并非一时兴起,因为在此之前,心理学、循证医学和社会学的学者就早已针对P值和使用P<0.05进行科学推断的弊端展开了激烈的学术争论,“地球是圆的(P<0.05)”早已成为讽刺滥用统计推断的经典笑话,这些现象引起了美国统计学会理事会的高度关注[1]。
2010年, Siegfried在《Science News》撰文言辞激烈地指出:“这是科学界中最不可告人的秘密:统计分析中检验假设的‘科学方法’建立在一个脆弱的基础之上”;2014年2月7日,他继续在《Science News》上撰文批评:“检验各种科学假设中用到的统计方法……比Facebook隐私条款中的缺陷还要多”。一周之后,Regina Nuzzo在《Nature》杂志科学方法专栏中发表了名为《统计误差》的论文[2],目前已成为该杂志阅读次数最多的文章之一。国内“果壳网”科学人专栏将此文进行了编译,取名为“统计学里‘P’的故事:蚊子、皇帝的新衣和不育的风流才子”,随后“数据工作室”微信公众号的推文《P值之死》在朋友圈和各类网络媒体中盛传。
2016年3月7日,美国统计学会执行主任Ronald L. Wasserstein代表美国统计学会理事会在《The American Statistician》杂志(网络版)上发表了名为《关于统计显著性与P值》的官方声明。之后,在中国统计学门户网站“统计之都”上,邱怡轩发表博文“美国统计协会开始正式吐槽(错用)P值啦”;2016年3月23日,在微信公众号“科研圈”上,谭坤编译了“美国统计学会权威发布:P值应该这么用,学界有错须改正”的有关内容。
P值究竟怎么了?统计显著性到底是否科学?鉴此,笔者从被误读与误导的P值入手,基于国内统计学教材和文献的“假设检验”内容,通过示例和几何图示,直观地解释P值、统计显著性与统计功效等不易理解的概念;回顾心理学统计研究经典文献《显著性误读:一个师生共存的问题》,讨论P值是如何被误读与怎样被误导的,并基于美国统计学会的官方声明,给出正确使用P值的建议。
二、假设检验、统计显著性与统计功效
(一)假设检验
1.假设检验的临界值法。目前,国内的《概率论与数理统计》和《统计学》教材中,都会至少用一章的内容介绍假设检验的基本原理与步骤。如果检验需要利用“Z检验(或t检验)的临界值表”,则被称为假设检验的“临界值法”,并已被广泛应用于实际问题中。在此,以“假设检验在审计抽样工作中的应用研究”为例[3],将教材所传授的假设检验“四部曲”总结如下:
第一步,根据实际问题的要求,提出原假设H0及备择假设H1。例如,假设X1, X2,…,Xn是取自正态总体N(μ,σ2)的一组样本,要检验如下假设:
H0:μ=μ0,H1:μ≠μ0(双侧检验;或H1:μ<μ0左侧检验;H1:μ>μ0右侧检验)。
第二步,根据总体分布情况及方差是否已知,选择合适的统计量。
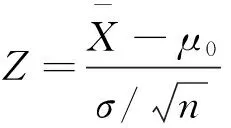
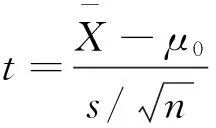
第三步,给定显著性水平α,确定相应临界值水平。显著性水平α表示假设H0为真时拒绝原假设的概率,也就是拒绝原假设所面临的风险,一般是人为给定,取值通常很小,如 0.1、0.05、0.01 等,表明原假设为真时,检验统计量落在其拒绝区域内的概率只有α,而落入其接受区域内的可能概率是 1-α 。
第四步,依据假设检验的规则,由样本数据计算出检验统计量的实际值,与查表获得的临界值进行比较,视实际值落入接受区域还是拒绝区域,做出是否拒绝原假设H0的结论。
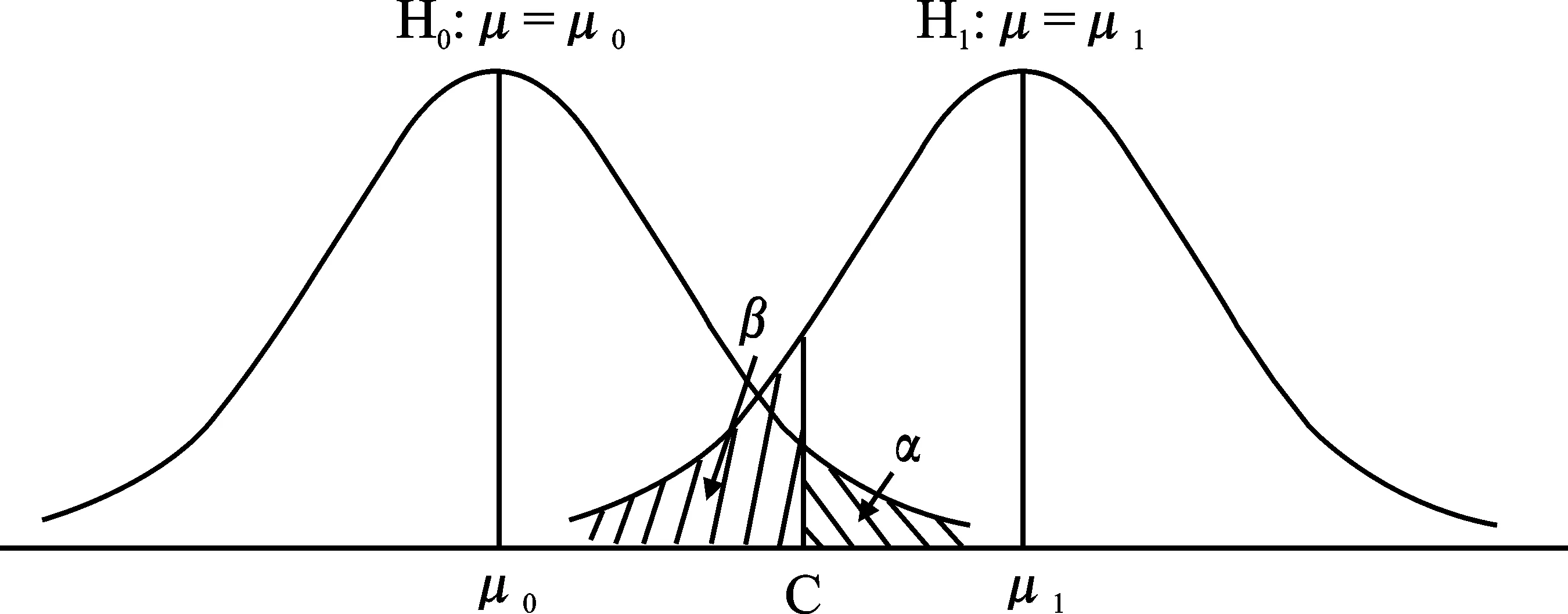
具体来说,当需要采用 Z统计量进行右侧检验时,检验规则为:当Z≥zα时,拒绝H0;当Z 2. 假设检验的P值检验法。随着计算机软件的普及和发展,在假设检验“临界值法”的基础上,部分教材还简要介绍了假设检验的P值检验法的一般步骤,并讨论了两种检验方法的区别[4]214-216。 “假设检验问题的P值是由检验统计量的样本观测值得出的原假设可被拒绝的最小显著性水平”,在现代计算机统计软件中一般都给出检验问题的P值,按P值的定义,对于任意给定的显著性水平就有: (1)若P值≤ α,则在显著性水平α下拒绝H0。 (2)若P值>α,则在显著性水平α下接受H0*正取的说法应为“不能拒绝”。。 P值法给出了拒绝H0的最小显著性水平,因此P值法比临界值法给出了有关拒绝域更多的信息。 3. P值的几何图示。我们以右侧假设检验H0:μ=μ0,H1:μ>μ0为例,图示临界值与P值的关系。假设显著性水平为α在H0为真的条件下,PH0(Z≥zα)=α (总体方差已知时的Z检验)。 zα为临界值,可通过标准正态分布表查出具体数值,如α =0.05时,zα= 1.65。P值是由检验统计量的样本观测值得出的原假设可被拒绝的最小显著性水平,正态分布概率密度函数条件下,假设检验的临界值和P值几何意义如图1所示。 (二)P值与统计显著性 1. P值。以上教材和文献中的P值概念比较晦涩难懂。美国统计学会的声明中也给出了P值的非正式定义:“P值就是基于某个特定统计模型之下, 图1 正态分布概率密度函数下临界值和P值图 对于数据的某个统计量(如两个对照组的样本平均值之差)与观测值相等或比观测值更极端的概率”,此定义也有些绕口,不易理解;百度或维基百科上关于P值的概念要相对精炼简要:“P值就是当原假设为真时,所得到的样本观察结果或更极端结果出现的概率”,但“更极端”的含义似乎也不够直观。 下面通过“硬币投掷”直观性试验,尽可能用非数学语言来解释以上P值的概念*更加深入浅出、图文并茂的解读详见谢益辉、胡江堂等在“统计之都”上的博文和张之昊在“协和八”微信公众号上连载的“说人话的统计学”系列。。 (1)原假设。你从钱包中拿出一枚硬币,随手向空中一抛。一般来讲,如果一枚硬币没有做假是“均匀”的,那么结果出现正面和反面的可能性(概率)应该都是1/2。现在,如何来证明你手中的硬币是“均匀”的呢? 除了直接观察,人们会想到用试验的方法来证明,即将硬币抛2次,结果2次都是正面或者2次都是反面,这时是否会怀疑你的硬币?假如结果正好是1正1反(或1反1正),是否能肯定你的硬币是均匀的?你可能不会轻易下结论,因为凭直觉会认为硬币抛2次太少了。以上每种结果的出现都很正常,此证据不足以否定硬币的“均匀”性。 增加投掷硬币的次数,即将硬币投掷5次,每次抛掷的结果都做记录;最后把出现正反面的次数分别统计,假设某一次试验的结果是:正面4次,反面1次,这时将如何判断硬币是否“均匀”呢? 按照R. A. Fisher(1890—1962)创建的“显著性检验(Significance Testing)”理论(注意:非J. Neyman(1894—1981)与E.S. Pearson(1895—1980)创建的“一致最优检验(Uniformly Most Powerul Test)”理论*两者的区别可参见Lehmann EL. The Fisher, Neyman-Pearson Theories of Testing Hypotheses: One Theory or Two? Journal of the American Statistical Association, 1993(88):1242-1249.),首先“假设”硬币是均匀的,也就是抛出来正面和反面的概率都是0.5,这就是P值定义里的“原假设”。 (2)所得到的样本观察结果或更极端结果出现。硬币试验中的“样本”就是抛5次硬币,得到了“4正1反”;如果抛了5次,得到的观察结果是“5正0反”,这就是比“样本4正1反”“更极端的结果”。 假设硬币是均匀的(“原假设”为真),连抛5次硬币得到都是正面的概率就是0.5的5次方,也就是0.031 25,这就是所定义的P值。换言之,这种结果的出现,在32次试验中才可能出现1次。 2. 统计显著性。从日常生活的经验中人们能感觉到,对于一块均匀的硬币来说,5次抛掷中可能性最大的结果应是“3正2反或3反2正”,而得到“4正1反”这样的结果就有些怀疑了*此例设计硬币投掷5次,是为了使概率计算过程简单,便于理解。实际上,试验次数设计偏少,若改为100次投掷后,结果90正10反,则更符合实际。,得到比“4正1反”更极端的结果“5正0反”实在是不太可能了。与其相信这样的小概率事件在一次试验中真的发生了,还不如怀疑“原假设”硬币均匀的正确性,而认为更合理的解释是这块硬币可能是“不均匀”的。 那么,多小的P值算是小呢?在统计学中,按惯例事先给出的界线是0.05,因为以上试验的样本结果为“5正0反”,则对应的P值=0.031 25,因为P值<0.05,所以就拒绝“原假设”,否定硬币的“均匀性”,这就是常见的“具有统计学意义上的显著性”,可以推断该硬币是一枚偏向正面的非均匀硬币。 P值的定义中蕴含了“显著性检验”的基本统计思维方法,这种统计归纳思维方法几乎被运用在所有学科领域的主流统计分析之中,对它的准确理解不仅是通向掌握各种具体统计学测试的大门,更影响着人们对统计分析结果的解读。 P值本质上是什么?它是基于特定假设和实际样本进行统计推断的一个工具。某种意义上说,P值体现了如果原假设成立时研究者看到样本的奇怪程度。P值越小,所获得的样本在原假设成立的前提下就越不可能出现;而当P值小到一定程度时,不得不认定其假设是错误的,因为可能性这么小的事件,实在是在一次试验中太难发生了。 根据P值进行统计推断的思想与数学中的反证法具有一定的相似性。但是,由于归纳与演绎逻辑的不同,两者有一个关键的区别,由于随机性的存在,在统计推断中无法像在数学反证法中一样千真万确地认定原假设是绝对错误的,只能根据“小概率事件在一次随机实验中不会发生”的原理做出有较大可能性推翻原假设的统计决策。 (三) 统计功效 1.第一类错误与第二类错误。统计功效与统计显著性有着极为密切的联系,而它们又都是建立在统计假设检验的两个基本概念“第一类错误”和“第二类错误”之上。为了更加生动形象介绍多数统计教材没有涉及的“统计功效”的概念与含义,用“背影识人”为例进行直观性说明: 某一大型商场的经理,在月末盘点时需要了解该月光临商场顾客中女性的比例。假设只有商场出口的监控记录可以调用,且监控摄像只摄录到了顾客出门时的头部影像而无法看到脸部,故只能从背部看清顾客头发的长短。那么,如何辨别顾客的性别呢?有人给出建议,即如果顾客是长发则为女性;如果顾客是短发则为男性。 改用统计学的语言来描述:由于旨在找出女性顾客,每当看到一个顾客背影的头像时,就先假设这是个女人(“原假设”)。如果此人头发太短,那就认为他不是女人(“拒绝原假设”); 如果此人头发够长,那就认为她是女人(“接受原假设”,更严格地说应为“不能拒绝原假设”)。 但是,这种判别方法可能会犯以下两类错误:一是把一小部分短发女人当成了男人,也就是在原假设其实为真时错误地拒绝之(弃真),这在统计学中被称为“第一类错误”;二是把另一小部分长发男人当成了女人,也就是在原假设其实为假时错误地接受之(取伪),这在统计学中被称为“第二类错误”。 2. 统计功效。教科书中通常用希腊字母α代表犯第一类错误的概率;β代表犯第二类错误的概率,α和β的几何意义如图2所示。在这个例子中,α就是被误判的女人在所有女人中的比例,而β则是被误判的男人在所有男人中的比例。 第一类错误与之前讨论的统计显著性密切相关,α就是事先给定的显著性水平(通常为0.05),之所以要在P值足够小的时候才拒绝原假设,就是为了让犯第一类错误的可能性尽可能低,而如何知道这个建议的最终识别率有多高呢?既然商场经理的目的是想区别出男性顾客,那就要看到底多大比例的男性顾客被识别了出来,这个比例就是1-β,即所有男人减去误判的男人(长发男人)在所有男人中的比例,“1-β”正是“统计功效”。 第一类错误用α值和P值来控制,第二类错误由什么来控制呢?用统计功效。统计功效指的就是:如果我们感兴趣的效应或差异的确存在,在给定的显著性水平的规定下能够正确地拒绝原假设的概率,这其实就是不犯第二类错误的概率,因此统计功效的值可以用1减去β得到。 在任何统计学问题上,以上两类错误都是此消彼长的。如果商场经理想少犯第二类错误,增加头发长度的标准,把中长发男性尽量排出,那么必然会有更多中短发女性被误判;相反,如果经理想少犯第一类错误,降低头发长度的标准,那么男性错判的可能性就增加了。 图2 假设检验犯两类错误概率示图 (一) 经典案例“显著性误读,一个师生共存的问题” 关于P值的争议由来已久,主要集中在大量应用统计假设检验进行实证研究的心理学和医学领域中。2000年,德国柏林自由大学(Free University of Berlin)教育科学与心理学系的Heiko Haller教授与马克思·普朗克人类发展研究所(Max Planck Institute for Human Development)的Stefan Krauss研究员,在德国的6所大学中进行了一项小型的关于“显著性(Significance)误读:一个师生共存的问题”的问卷调查[5],调查结果大大出乎他们的意料。 此次问卷的调查对象是德国6所大学的心理学系师生。调查对象被分成三组:第一组是教师组(N=30名),包括给心理学系学生讲授统计学和假设检验的教授和辅导新生的高年级研究生助教;第二组是研究员组(N=39名),包括没有讲授统计学的教授和研究人员;第三组是学生组(N=44名),全部由心理学专业的学生组成。 问卷非常简短,只包含一个问题和6个“是非”选项:“假设你进行了一项对照组试验,需要比较两组实验结果的均值(每组样本个数为20),采用的方法是独立均值t检验,检验结果为:t = 2.7,df(自由度)= 18, p(P值)= 0.01。”请判断以下6个陈述是“正确”还是“错误”(“错误”意指该陈述不能由以上检验结果得出,以下错误结果可能不止1个)。 1.你可以完全否定“总体均值无差异”的原假设。[ ]正确/错误[ ] 2.你已经知道了原假设为真的概率。[ ]正确/错误[ ] 3.你可以完全肯定“总体均值有差异”的备择假设。[ ]正确/错误[ ] 4.你可以推断出备择假设为真的概率。[ ]正确/错误[ ] 5.如果你决定拒绝原假设,你就可以推断你做出错误决定的概率。[ ]正确/错误[ ] 6.如果以上同样的试验重复很多遍,将有99%的试验获得显著性的结果。[ ]正确/错误[ ] Haller教授与Krauss研究员将113份有效调查问卷进行统计分析,最终结果如表1所示。表1中的比率值为各组回答的“错误率”,即在每组参加调查者的回答中至少出现一个错误的人数占小组人数的百分比;表1第4列的比例是Oakes在1986年所做类似研究的结果。 表1 2000年德国六所大学师生关于“显著性误读” 问卷调查结果比较表 注:资料来源于参考文献[5]。 (二)P值被误读的原因分析 Haller教授与Krauss研究员对以上调查结果表示极其惊讶,“尽管Oakes(1986)的调查结果和研究著作发表已经过去了15 年,而且有关讨论显著性检验误解的论文也发表了很多篇,但是似乎一切都没改变”。*2015年,笔者也将以上问题对30名统计专业的本科生进行了调查。同样,距离2000年德国大学的调查,15年时间过去了,我们的结果也惊人地相似,学生组错误率100%,没有1名学生全部答对。 表1显示,问卷调查结果中学生组全部答错,错误率100%;近 90%的心理学科学研究人员至少将一个含有错误“意义”的P值误认为是正确的;更加重要的是,造成以上结果的重要原因在于,讲授假设检验方法的教师们的错误率也高达80%,可以想象他们对显著性的“误解”正在课堂的讲解中一遍又一遍地重复,不断“误导”着一批又一批的学生,对于这种现象,两位学者表示“实在是令人目瞪口呆、无言以对”。 事实上,Haller教授与Krauss研究员调查问题中的6个“是非”陈述选项答案全是错误的。 陈述选项1 和 3 容易答对,两者的错误比较明显:显著性检验绝对不能证明 (或否定) 假设;显著性检验只能提供“可能的”信息,这些信息最多只能用来对某些理论进行印证;统计推断不可能得出“完全肯定(或否定)”的“绝对”结论。 一般来说,通过显著性检验不可能得到任何假设成立的概率:既不能得到概率值为1(陈述选项1 和 3) 也不能得到其他概率值 (陈述选项2 和 4)。所以,陈述选项2 和 4也都是错误的。对假设给出概率的描述只可能在贝叶斯统计中出现[6]。 陈述选项 5 看起来与第一类错误的定义非常相似(即当原假设为真时拒绝原假设的概率),但实际上如果你决定拒绝原假设 (陈述选项 5所述 ),当且仅当原假设是正确的情况下,你的这个决定才是错误的,因此在陈述选项 5中的“概率 ”(“你做出错误决定”) 其实是“原假设”为真的概率,而这个概率如选项 2所述,是不可能由这种检验方法得到的。 陈述选项 6是所有选项中极易混淆的难题,它实际上反映的是所谓“重复谬误”。在Neyman 和 Pearsons的检验范式中,以频率学派的观点,可以通过P=0.01解释 “如果原假设为真,在多次重复试验中拒绝原假设的相对频率”,但在本例中你只进行了一次试验,没有证据证明原假设是真的。在许多人的脑海里,会对“P=0.01”的含义“过度”引申,将1-p错误地演变成拒绝原假设的相对频率,即显著性结果可以被重复的概率。实际上,如果你将以上同样的试验重复多遍,由于影响试验条件的不确定性,你很难每次试验都获得显著性的结果。 所以,我们不能简单地停留在“P值是什么”的问题上,而要将重点放在“P值为什么”,而真正理解“统计显著性”,又要从了解“P值不是什么”开始。 P值是目前科学界广泛使用的主流统计学方法中最重要的一个概念,同时也可能是被误读和误导最多的一个概念。翻阅各学科的文献,很容易就发现对P值的错误理解和表述,即便是发表在《Science》和《Nature》之类顶级期刊的文章也不可避免。 对P值定义的误解一般可分为两个层面:一是基本层面,将P值简化误认为“P值是原假设为真的概率”;二是引申层面,先按“原假设为真”推断至“备择假设为假”,再将“P值是原假设为真的概率”引申到“P值是备择假设为假的概率”。 当P值很小时就拒绝原假设,认为备择假设是真的吗?那难道不是说P值代表原假设有多真吗?不是,这个问题最简单的解释是:对于任何一个假设它为真的概率都是固定的。然而,已经知道P值是根据具体的样本数据计算得出的,同样的实验重复做几次,每次得到不同的样本,P值也自然会有区别。因此,P值不可能是原假设为真或备择假设为假的概率。 进一步,回顾“显著性检验”的统计思维逻辑:P值越小,样本提供的支持“原假设正确”的证据就越少,少到一定程度时则可以(统计)推断原假设是不正确的。P值只描述样本与原假设的相悖程度,原假设的真与假是我们“仅仅以一次试验观察为根据”做出的一个判断。事实上,P值并不是刻画“原假设为真假”或“备择假设为真假”的概率。 所以,P值既不是原假设为真或假的概率,也不是备择假设为真或假的概率。目前,所广泛使用的一整套统计推断和假设检验方法及其思想体系,均属于统计学的 “频率学派”,P值能做的就是在特定的原假设条件下,对数据未知特征进行推断分析。但是,如果要对这些假设本身作出判断,仅凭数据本身是不够的,还需要根据相关学科的理论知识,了解研究对象中除了人们感兴趣的假设以外其他假设存在的概率。 实际上,假设本身成立与否的概率是统计学科中另一个近年来日渐受到重视的流派“贝叶斯学派”试图解决的问题[7]。随着大数据时代的到来和计算机技术的发展,需要大量计算辅助的贝叶斯统计方法逐渐受到了重视[8],也有不少统计学者呼吁学术界应当用贝叶斯方法补充如今仅以P值为中心的频率学派方法。 P值只是在特定数据和模型的条件下,利用显著性检验理论框架进行统计推断,以表明总体未知特征是否具有统计显著性的一个简化阈值标准。但是,随着研究问题的复杂性和不确定性的增加,P值已逐渐被研究人员“异化”成为论文能否发表的“关键之值”,部分研究人员似乎忘了研究本来的真正目标,而是将研究目的变为竭尽全力追逐一个小于0.05的P值。进而,一个小小的P值引发了许多重大的“科学”发现。 由于在各学科实际问题的数据统计分析研究中,P值经常被误读和滥用。鉴于此,美国统计学会在声明中提出了以下6条正确使用P值的准则[1]。笔者基于这6条准则,建议在理论探讨和应用研究方面注意以下三方面的问题: (一) 重点关注P值的“一个可以,三个不能” 对于一个特定的数据集,常用的研究方法是对此数据集在一定的假设条件下设定一个模型,由于不确定性,数据与模型之间总会存在不相容性,将这些假设的条件与设定的模型统称为“原假设*也翻译成“零假设”,心理学中常翻译成“虚无假设”。”。一般来说,“原假设”表示某种效应不存在,例如两个试验组之间不存在差异,或一个因素与一种结果之间的没有关系。如果在给定的“原假设”(假设的条件与设定的模型)下计算得到了一个P值,而此P值越小,数据与“原假设”之间统计的不相容性就越大,这种不相容性可以用来诠释对“原假设”存疑的程度,或提供反对“原假设”成立的证据。所以,P值可以表明数据与一个设定统计模型之间不相容的程度。不过,对于研究者来说,更加重要的是要特别关注P值的“三个不能”。 1.P值不能度量某个研究假设为真或假的概率,也不能度量数据仅由随机因素影响的概率。研究人员非常希望将P值转化成一个“原假设”为真的证据,或者能够度量观测数据仅由随机事件造成的概率,但P值两者都做不到,P值只能解释数据与特定假设之间的关系,而并不能解释假设本身。 2.P值或统计显著性并不能度量某个效应的大小,也不能度量某种结果是否重要。统计上的显著性并不等于科学、人文或经济上的重要性。较小的P值并不一定意味着有更大或更重要的效应;较大的P值也不代表重要性缺乏或更小的效应。所以,不管某个效应的影响有多小,当样本量足够大或测量精度足够高时,有可能得到一个较小的P值;反之,无论某个效应影响有多大,当样本量很小或测量不精确时,也可能会得到一个较大的P值。相类似,对于相同的估计效应,当估计的精度不同时也会得到不同的P值。 3.P值本身并不能对统计模型或研究假设的可信度进行一个充分的评价。研究者应该在研究中清楚地意识到:在没有充分的专业理论背景和其他相关证据时,P值所能表示的信息极其有限。例如以0.05为标准,较小的P值只能为拒绝“原假设”提供非常弱的信息。同样,相对较大的P值也不一定意味着信息就偏向支持“原假设”,因为可能还有其他的“假设”与观测数据具有更强的一致性。因此,如果还存在其他可靠的研究证据,研究者对数据的分析就不应仅仅停留在对P值的计算上。 (二) 基于P值的推论需要完整的研究报告和透明的研究过程 研究者不应选择性地报告P值和相关分析。某项研究可能使用了多种分析方法,而研究者只报告其中的一部分P值的结果(特别是那些通过显著性标准的),这些P值难以从本质上解释研究结论。在已发表的文献中,用“樱桃采摘式”的只挑好不选坏的研究方法,诸如数据疏浚、 显著性追逐、 显著性探索、 选择性推断和“P值黑客”,得到了许多虚假的统计显著结果。如果不对问题进行多项统计检验,容易产生如下结果:无论研究者选择哪种基于统计结果的结论,由于读者无法得知研究者所采用的全部依据和选择,研究结果的有效性就打了大大的折扣。研究者应该尽量展示研究过程中所使用过的假设、所有数据收集的过程、所有进行的统计分析和所有计算得到的P值。如果连进行了多少次分析、进行了哪些分析以及得到了什么样的分析结果(包括P值)都不知道,基于P值和相关统计量的研究结论就不能推断出有效的科学结论。 (三) 科学研究的结论、商业企业的决策或公共政策的制定,都不应该只取决于看一个P值是否达到了一个认为给定的标准 在实践中,为了给某种科学主张或论断提供佐证,将数据分析或科学推断简化为一个机械的“明线”规则 (如“P< 0.05”) ,这种做法可能会导致错误的结论和失误的商业决策。事实上,一个科学结论的正确与否,并不会随着研究者算出的P值大于还是小于0.05而改变。研究人员需要将更多专业理论背景和其他相关证据纳入到科学推断的过程中,包括研究的有效设计、样本数据的质量评价、研究问题的非样本信息以及数据分析时所采用的合理假设等。出于简化实用的考虑,商业决策者常需根据研究结论做出“是与否”的决策,但这并不意味着仅凭P值本身就可以单独断定这一商业决策的正确与否。 总之,数据分析不能仅仅局限于计算P值,而应探索其他更拟合数据的模型。科学的世界中,不存在哪个单一的指标能替代科学求真的思维方式。 大数据时代,小小的P值已引起了国际学术界和美国统计学会理事会的高度关注,因为它对统计学的科学性提出了严重质疑。所以,希望国内相关部门也能引起高度重视,将以上P值的“注意事项”早日编入中国的统计教科书,重编假设检验相关章节,不要再让美国教授嘲讽“我们教它是因为我们用它,我们用它是因为我们教它”的这种循环误导、以讹传讹的现象,在中国的大学和研究生院里继续重演。 [1] Wasserstein R L, Lazar N A. The ASA's Statement on P-Values: Context, Process, and Purpose[J]. The American Statistician, 2016 (3). [2] Nuzzo R . Statistical Errors[J]. Nature, 2014 (2). [3] 王芳,王景东. 统计假设检验在审计抽样工作中的应用研究[J]. 审计研究,2010(5). [4] 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 4版.北京:高等教育出版社,2008. [5] Haller H, Krauss S. Misinterpretations of Significance: A Problem Students Share with Their Teachers? [J]. Methods of Psychological Research, 2002(7). [6] 丁东洋,周丽莉. 基于贝叶斯方法的信用评级模型构建与违约概率估计[J]. 统计与信息论坛, 2010(9). [7] 王佐仁,杨琳. 贝叶斯统计推断及其主要进展[J]. 统计与信息论坛,2012(12). [8] 刘乐平,高磊,杨娜. MCMC方法的发展与现代贝叶斯的复兴——纪念贝叶斯定理发现250周年[J]. 统计与信息论坛,2014(2). (责任编辑:郭诗梦) Statistical Significance a Misreading of P-Values:Based on the Official Statement of ASA HAO Li, LIU Le-ping, SHEN Ya-fei (Big Data Statistics Research Center, Tianjin University of Finance and Economics, Tianjin 300222, China) After the ASA's statement on p-values and significance, p-value was brought to the attention of the scholars. The paper briefly explains p-value, statistical significance, and statistical power concepts, through "Coin-Throwing" and "Hair Length Determine Person's" intuitive examples, analysis the reason of p-value misreading with the classic case of psychological statistics. The paper strongly recommends that researchers in accordance with the "Six Principles" of proper use the p-value, based on the official statement of ASA. statistical significance; p-values; psychological statistics; Bayesian statistics 2016-04-06;修复日期:2016-10-11 国家社会科学基金项目 《基于大数据分析的城市社区养老模式研究》(15BRK002) 郝 丽,女,安徽寿县人,经济学硕士,副教授,研究方向:体育与健康大数据统计分析; 刘乐平,男,江西萍乡人,经济学博士,教授,博士生导师,研究方向:贝叶斯数据分析,精算与风险管理; 申亚飞,男,山西黎城人,硕士生,研究方向:大数据统计分析。 C829.29∶O211.9 A 1007-3116(2016)12-0003-08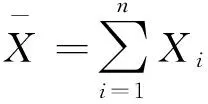

三、P值误读经典案例及其原因分析

四、正确使用P值的建议

