云南省测绘成果向2000国家大地坐标系转换的方法

周峻松，李石华,，李文华，彭双云

(1. 云南省基础地理信息中心，云南 昆明 650034； 2. 云南师范大学旅游与地理科学学院，云南 昆明 650500)



云南省测绘成果向2000国家大地坐标系转换的方法

周峻松1，李石华1,2，李文华1，彭双云2

(1. 云南省基础地理信息中心，云南 昆明 650034； 2. 云南师范大学旅游与地理科学学院，云南 昆明 650500)

以国家测绘地理信息局对2000国家大地坐标系(CGCS2000)推广使用的要求为指导，根据坐标系建立的原理，结合云南省现有测绘成果实际，利用布尔莎七参数模型和栅格模型法，开展了云南省省级基础测绘成果由1954北京坐标系、1980西安坐标系向2000国家大地坐标系转换方法研究。结果表明：①两种方法的残差中误差均在其反转时的残余误差范围内，证明了七参数法和栅格模型法是可靠的；②从对两种方法的检验结果来看，模型法比栅格法的改算点位残差小；③栅格模型改正法可用于高精度要求的坐标改算，而七参数法可用于对精度要求不高或需要保持旧成果整体精度的坐标转换。

1954北京坐标系；1980西安坐标系；2000国家大地坐标系；坐标转换；布尔莎模型；栅格模型

此前，关于启用2000国家大地坐标系(CGCS2000)的提议已获国务院批准，国家测绘地理信息局规定：自2008年7月1日启用CGCS2000，并用8～10年的时间完成现行国家大地坐标系向CGCS2000的过渡和转换。国家测绘地理信息局提供了CGCS2000的技术参数，并对新旧坐标系的转换和使用作出了说明。由于1980西安坐标系已采用20多年，大量的测绘成果都采用的是1980西安坐标系，甚至是1954北京坐标系[1]，因此面临着大量的坐标转换问题。众多学者就其转换方法开展了深入研究与试验[2-5]，其研究思路与方法可为后续研究提供借鉴与参考。

根据国家测绘地理信息局《关于加快2000国家大地坐标系推广使用的通知》(国测国发〔2013〕11号)的要求，尚未开展此项工作的省份，应尽快完成各自省份地理信息成果的梳理、省级成果转换，推动市县级成果转换。为此，云南省测绘地理信息局将该项工作作为2014年度基础测绘任务之一，由云南省基础地理信息中心承担并完成“云南省基础测绘成果2000国家大地坐标系转换”任务。本文分析了现有坐标系转换方法，在调研其他省份的工作经验与充分分析相关文献研究结论的基础上，结合本省基础测绘成果和地域实际，有必要就省级测绘成果坐标系转换方法展开研究，以期为1954北京坐标系、1980西安坐标系向CGCS2000转换方法提供案例。

一、资料利用与转换方法

1. 资料利用

本研究中充分利用了国家、省级、地方现有的测绘成果。具体包括：

1) 云南省内的天文大地网与高精度GPS2000网联合平差地面网点CGCS2000成果2168个点，但经过与现有的旧成果进行人工比对、检核和甄别，预选2100个点作为公共已知点使用。

2) 为改善已知点的图形分布结构、提高转换精度，从西安大地数据处理中心补充收集到省外周边428个点CGCS2000坐标系成果、省内68个点1980西安坐标系与1954北京坐标系的成果。经过与现有的成果比对，将343个点(省内68个点、省外275个点)作为预选公共已知点使用。

3) 似大地水准面精化成果(CGCS2000坐标系)，获取高程异常值，将正常高换算为CGCS2000坐标系大地高。

4) 利用《1980西安大地坐标系统成果图集》，采集其中的1954北京坐标系、1980西安坐标系高程异常图等值线，用于高程异常值空间分布的内插，获取高程异常值。

5) 国家测绘地理信息局提供的“1980西安坐标系到CGCS2000坐标系空间格网改正量”，主要用于结果比较及检验。

6) 云南省1980西安坐标系、2000国家大地坐标系两套成果的GPS B级点31个点、GPS C级点1311个点，作为结果的检验。

7) 以似大地水准面精化工作时联测转换的成果40个点作为结果检验。

8) 利用少量国家Ⅱ等点的控制成果。联测了安宁、玉溪交接区域的高鲁山Ⅱ、鸡背山Ⅱ、大黑山(二)Ⅱ，对送鬼山ⅢⅡ进行了联测检验工作。

2. 转换方法

利用布尔莎模型系统转换后，在已知点上还有残留误差，且各已知点的模型误差表现出明显的区域差异性。而这种区域差异性期望用一种二维空间场模型来描述，常用的场模型有6种(如图1所示)。

图1 二维空间场模型

这些场模型的核心是利用已知点进行空间插值。空间内插可分为几何方法、统计方法、空间统计方法、函数方法、随机模拟方法、物理模型模拟方法和综合方法[6]。其中几何方法主要是基于“地理学第一定律”的基本假设[7]，即邻近的区域比距离远的区域更相似。最常用的几何方法有泰森多边形(最近距离法)和反距离加权方法。反距离加权法是最常用的空间内插方法之一，认为与未采样点距离最近的若干个点对未采样点值的贡献最大，其贡献与距离成反比可表示为

(1)

式中，Z为待插值的栅格点；Zi为第i个已知点的改正值；di为拟合点到第i个已知点的大圆距离；n为用于拟合插值的已知点的数目。

用该方法计算出每一个点空间分布的模型残差改正值，最后形成两个二维分量上的改正量栅格集，在本研究中将其定义为栅格改正法。

移动拟合法的计算模型中，其定权用的是空间直线距离d，而在实际操作时用的是地理坐标，其计算的距离与空间直线距离有一定差异。但由于其作用范围只是附近的点，比较地理坐标距离计算的权值与空间直线距离计算的权值发现，其权值的比重基本一致，而计算工作量得到大大简化，故用地理坐标代替计算。

二、计算过程与结果分析

1. 布尔莎模型七参数解算

在求解七参数时，先将大地坐标转换到空间直角坐标系下，再求解七参数，流程如图2所示。

图2 计算流程

(1) 大地坐标与空间直角坐标系之间的转换

大地坐标(B、L、H)转换为空间直角坐标(X、Y、Z)的公式为

(2)

空间直角坐标(X、Y、Z)转换为大地坐标(B、L、H)的公式为

(3)

式(3)用迭代法计算。

(2) 七参数转换

七参数转换模型采用布尔莎模型，它在两空间直角坐标系之间存在严密的转换关系，其形式非常简单，物理意义也非常明晰，即

(4)

式中，(X1，Y1，Z1)为原坐标系下三维坐标；(X2，Y2，Z2)为新坐标系下三维坐标；ΔX、ΔY、ΔZ、εX、εY、εZ、m为7个参数。

通过这样的过程改进，不但计算结果更为精确，7个参数的物理含义也很明晰。

(3) 转换步骤

1) 利用GPS C级点计算的1980西安坐标系/1954北京坐标系→CGCS2000坐标系的参数，将参与1980西安坐标系/1954北京坐标系天文大地网联合平差的地面网点概略改算到2000国家大地坐标，然后根据点名、点位(B，L)，对照CGCS2000系成果查找重合点。以此为基础，利用新旧成果的正常高信息，检查正常高是否发生大的变化，以此来确认该标石是否发生变动，进一步甄选重合点。

2) 将重合点坐标换算为大地坐标及空间直角坐标。

3) 使用筛选出的全部重合点求取转换参数(三维转换)，再利用该转换参数回代，求得已知点的坐标，计算已知点的残差。

4) 分析残差值大于2～3倍残差中误差的点的可靠性，检查点位和成果的正确性，重新确定重合点。

5) 再重复步骤3)和4)，直到回代残差到一定范围内为止，最终确定参与求解参数的已知点。

根据上述步骤，可计算出1980西安坐标系/1954北京坐标系→CGCS2000坐标系的参数(见表1)。

表1 七参数及中误差统计

2. 栅格法改正模型

(1) 改算步骤

①甄选已知点，剔出与周围互差较大的异常点；②确定栅格改正量的空间格网大小；③根据已知点分布及空间插值特点，划定栅格改正量的有效范围；④计算经度B、纬度L两个分量的栅格改正量；⑤结果检验。

(2) 改算过程

1) 根据已知点改正量，利用TIN计算已知点构成的每一个三角区的变化梯度，得出已知点经度、纬度改正量的差分值，在不影响使用精度的前提下确定格网大小。其中，纬度的残差梯度最大值0.002 45°、经度的残差梯度最大值0.003 72°，对应到平面距离上，每1000 m分别对应64.9、42.8 mm。

2) 经反复试算得出，改正量的格网大小为100 m时，在改正量变化最大的区域，由规则格网存储引起的误差：在X方向<6.49 mm、在Y方向<4.28 mm。因此，本省改正量的格网大小定为100 m左右(实际执行为3″)。

3)虽然收集了云南省周边一定缓冲区域的已知点成果，但云南地处边境，国外部分没有可用的已知点。并且采用的IDW方法要对已知点的残差改正量进行空间插值，该方法具有一定外推特性，若外推距离远，则精度低。结合现有已知点及本省1∶1万地形图生产的需要，确定了栅格改正量的有效值范围。

(3) 栅格改正量的计算

利用布尔莎模型系统转换后，在已知点上还有残留误差，可对这些残差再次进行改正。利用式(2)计算各栅格点的残差改正量，再利用模型计算系统改正量，两者叠加(系统+残差)形成最后成果。

3. 精度评定

模型坐标转换的精度是通过求取转换参数的重合点的残差来体现的。坐标转换精度估计依据以下公式计算

1) 残差V=重合点转换坐标-重合点已知坐标。

2) 空间坐标X与平面坐标x的残差中误差为

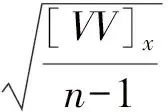
(5)

3) 空间坐标Y与平面坐标y的残差中误差为

(6)

4) 空间坐标Z与大地高H的残差中误差为

(7)

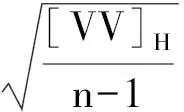
(8)

此外，对转换成果还采用了外业联测检测和与GPSC级点成果进行对比检验的方式开展了精度检核工作。

(1) 七参数模型计算精度评价

此次验证工作，使用的点共有2443个，其中已知点1222个、检验点1221个。为验证“模型残差(已知点残差中误差)”评定指标的可靠性，将筛选出一半的重合点用作已知点计算模型参数，而另一半重合点用作检验点进行改算精度检验。七参数模型的误差见表2。最后，再与全部作为已知点的模型残差作比较(见表3)。

表2 七参数模型误差统计

表3 模型残差与检验中误差的比较 m

从表3可以看出，1222个点与2443个点的模型残差与1221个点的检验中误差基本相当。再从检验中误差的大小、空间分布(图略)上看，两者也基本一致。

依据式(6)—式(8)可计算出，1980西安坐标系到CGCS2000改算模型残差：RMS dS=0.283 69 m，dS<0.3 m的占73.33%，最小值为0.012 002 m，最大值为0.88 m，在贡山县境内(麻纪娃Ⅱ)；1954北京坐标系到CGCS2000改算的模型残差：RMS dS=0.718 46 m，dS<0.5 m的占61.2%，最小值为0.011 4 m，最大值为3.124 m，在贡山县境内(卡瓦嘿Ⅱ)。转换模型残差区间统计见表4。

从表4中可以看出，1980西安坐标系到CGCS2000改算模型残差和1954北京坐标系到CGCS2000改算的模型残差差异较大，各点位差值范围的统计比例差异明显。1980西安坐标系到CGCS2000改算模型残差的点位误差差值范围集中在[0～0.15]、[0.15～0.3]，占73.33%；而1954北京坐标系到CGCS2000改算模型残差的点位误差差值范围集中在[0.3～0.5]、[0.5～0.883 6]，占63.67%。

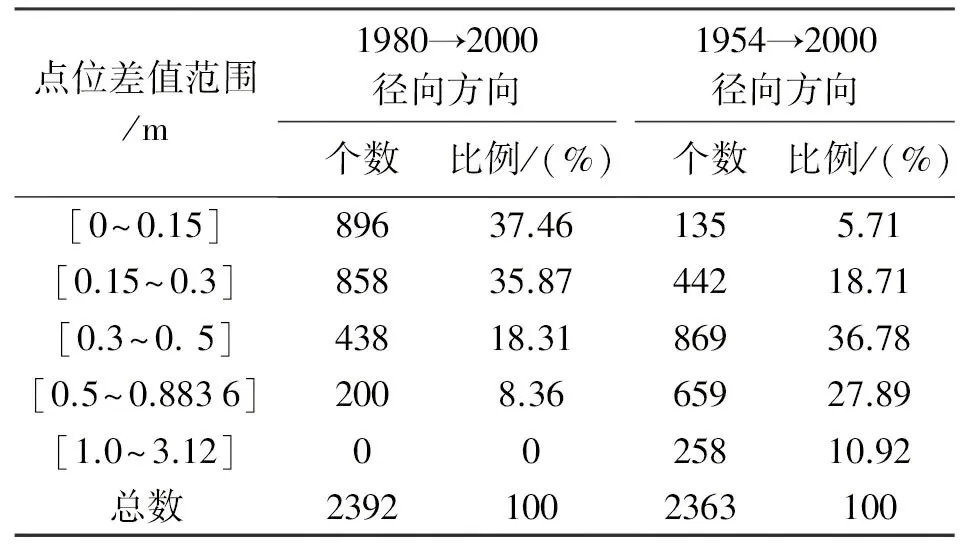
表4 转换模型残差区间统计

(2) 栅格模型计算精度评价

按照常理，改正量在空间分布上不应有大的突变；另外，按照计算改正量公式(式(2))的特点，在已知点上应有残差为0的特性。

① 图面检验

对1980西安坐标系到CGSC2000的经度(dL)、纬度(dB)，分别用色彩表示(图略)，色彩过渡均匀，没有突变现象。

对1954北京坐标系到CGCS2000的经度(dL)、纬度(dB)，分别用色彩表示(图略)，除西北角色彩稍有不均匀外，其余色彩过渡均匀，没有突变现象。

② 已知点残差检验

1980西安坐标系已知点残差检验，对在有效范围内的2374个已知点，读取栅格改正量、转换到CGCS2000后，与国家新成果比较，差异均为0，说明1980西安坐标系栅格改正量正确。

1954北京坐标系已知点残差检验，对在有效范围内的2369个已知点，读取栅格改正量、转换为CGSC2000后，与国家新成果比较，差异均为0，说明1954北京坐标系栅格改正量正确。

对1980西安坐标系转换为CGCS2000检验：栅格法计算2392个已知点的平面位置残差，结果均为0；对1954北京坐标系转换为CGCS2000检验：计算2369个已知点的平面位置残差，结果均为0。说明栅格法坐标改正量计算正确。

(3) 其他检验

利用国家测绘地理信息局提供的云南省1311个1980西安坐标系、CGCS2000的GPS C级点两套成果，通过筛选128个重合点，利用布尔莎七参数坐标转换模型解算CGCS2000成果。经检验，模型法转换平面位置残差中误差为0.110 m；栅格法转换平面位置残差中误差为0.287 m。

三、结 论

本文根据云南省基础测绘成果坐标转换的工作需求，基于坐标系建立的原理，对其转换方法进行讨论与分析，并对结果进行验证，结论与建议如下：

1) 利用七参数方法和基于七参数的栅格模型改正方法对云南省的基础测绘成果数据进行CGCS2000大地坐标改算，从概算精度的评价结果来看，两种方法是可靠的，均可使用。

2) 从两种方法的检验结果来看，模型法比栅格法的改算点位残差要小，但这不能说明模型法的结果更好，只能说明模型法与国家测绘地理信息局的转换法方法更接近。栅格改正法可用于高精度要求的坐标改算。对精度要求不高或需要保持旧成果整体精度的场合，只需利用七参数方法进行改正即可。

3) 在高等级控制点较稀少的地区，可酌情考虑选用三、四等控制点成果作为已知点，以保证图形结构。

4) 由于空间坐标转换需要用到大地高，而GPS测量可直接获取大地高，CGCS2000的新成果就直接提供了大地高。但1954北京坐标系、1980西安坐标系不是真三维空间的坐标，其提供的正常高成果是通过水准、三角高程测量得出的，与坐标成果是相互独立的，大地高需要间接推算获取。王文利等的研究结果表明[8]，重合点的大地高误差对布尔莎参数模型转换的平面结果影响较小，大地高误差在10 m以内时，基本不影响转换的平面结果。而转换点的大地高误差对布尔莎七参数模型转换的平面结果影响非常小。转换点大地高误差≤100 m时，可用正常高代替大地高进行转换，且转换结果不受影响。因此，在本次研究中，1954北京坐标系、1980西安坐标系的高程异常值可通过《1980西安大地坐标系统成果图集》获取，且精度不受影响。

5) DEM、DOM数据由于生产单位提交的原始数据部分缺少坐标信息，没有头文件或头文件格式不对的均转换失败，须补充头文件，手工将头文件里的坐标值加改正量平移。

6) 靠近中央子午线的图幅，DLG数据中的部分要素难以获取改正量，需重新设置带号进行转换。

[1] 钟业勋,童新华,王龙波.从1980西安坐标系到2000国家大地坐标系的坐标变换[J].海洋测绘,2010,30(1):1-3.

[2] 过家春,赵秀侠,吴艳兰.空间直角坐标与大地坐标转换的拉格朗日反演方法[J].测绘学报,2014,43(10):998-1004.

[3] 王海栋,柴洪洲,宋国大. 大地坐标系换代对海图的影响分析[J].测绘通报,2009(1):6-9.

[4] 曾安敏. 基于拟合推估的1980西安坐标系到2000国家坐标系的变换[J].大地测量与地球动力学，2008,28(5):125-128.

[5] 吕志平,魏子卿,李军,等. 我国CGCS2000高精度坐标转换格网模型的建立[J]. 测绘学报,2013,42(6):797-791.

[6] 李新,程国栋,卢玲.空间内插方法比较[J].地球科学进展,2000,15(3):260-265.

[7] 李小文,曹春香,常超一.地理学第一定律与时空邻近度的提出[J].自然杂志,2007(2):69-71.

[8] 王文利,郭春喜,程传录.大地高误差对Bursa七参数平面转换精度的影响[J].测绘科学,2011,36(5):37-38.

Study on Coordinate System Conversion Methods from BJ54，XA80 to CGCS2000 of Surveying and Mapping Archives in Yunnan Province

ZHOU Junsong，LI Shihua，LI Wenhua，PENG Shuangyun

2016-07-19

国家自然科学基金(41561086)；国家测绘地理信息局地理国情监测示范项目(测国土函〔2014〕35号)

周峻松(1968—)，男，高级工程师，主要从事地图制图、遥感与地理信息工程和应用项目管理等工作。E-mail: 78121467@qq.com

李石华。E-mail：lsh8010@163.com

周峻松，李石华，李文华，等.云南省测绘成果向2000国家大地坐标系转换的方法[J].测绘通报，2016(11)：80-84.

10.13474/j.cnki.11-2246.2016.0371.

P258

B

0494-0911(2016)11-0080-05