基于散射特性的单脉冲角跟踪雷达相干干扰方法*

陈秋菊,莫翠琼,孙 杰,戴幻尧

(1 电子工程学院,合肥 230037;2 中国洛阳电子装备试验中心,河南洛阳 471003)



基于散射特性的单脉冲角跟踪雷达相干干扰方法*

陈秋菊1,莫翠琼1,孙 杰1,戴幻尧2

(1 电子工程学院,合肥 230037;2 中国洛阳电子装备试验中心,河南洛阳 471003)

当雷达目标为复杂目标时,目标回波相位将受目标复杂的散射特性影响,传统的两点源相干干扰方法无法产生与目标回波相干的信号。针对该问题,基于目标的电磁散射特性,利用目标多散射点模型来调制接收到的雷达发射信号,以产生与目标回波具有相对稳定相位关系的干扰信号。为合理评估该技术的效果,根据单脉冲角跟踪雷达的典型应用场景,建立了单脉冲角跟踪末制导雷达作战模型,包括信号产生、处理模型及弹道模型,并搭建了闭环仿真平台;在该仿真平台上,进行了干扰效果验证实验,实验结果可为战术巡航导弹对抗研究提供有效和实际的参考依据。

相干干扰;单脉冲角跟踪雷达;目标散射特性;信号仿真

0 引言

单脉冲角跟踪雷达在一个脉冲内即可提取跟踪误差信息,测角既快又准,因此在机载雷达及末制导雷达等平台中获得了广泛应用。对这类雷达,传统的干扰方法包括噪声干扰、两点源干扰等,其中最常用的是相干两点源干扰[1-4],即在目标外布设干扰源,对入射信号直接射频存储,随后调制为与点目标回波有固定相位关系及相近幅度的信号[3],利用相位波前失真实施干扰。在相干两点源干扰方法的干扰信号产生过程中,对目标调制信息往往利用点目标模型来近似。对简单目标而言,依据点目标产生的相干干扰可以满足要求。但实际作战中,如果目标相对于雷达为复杂目标,则回波相位所受目标自身散射特性调制的影响则不容忽视[6-7]。此时,目标外布设的干扰源如果仅仅简单按点目标产生干扰,将无法真正与回波相干。

文中基于复杂目标的散射函数,研究针对单脉冲角跟踪雷达的相干干扰方法。利用相应姿态角下被掩护目标的散射函数对接收到的发射信号进行调制,以便保留目标散射特性对信号相位的调制信息,在此基础上产生与复杂目标回波具有稳定相位关系的干扰信号;为合理评估该方法的效果,以单脉冲角跟踪雷达在末制导雷达场景下的应用为例,设计了末制导雷达系统仿真模型及导弹六自由度弹道模型,完成了闭环仿真平台;基于该平台的干扰效果验证实验表明,与传统的相干两点源干扰相比,基于散射特性的相干干扰方法可以导致更大的脱靶量,具有更有效的干扰效果。

1 相干两点源干扰原理分析

相干两点源是在目标外,雷达跟踪波束内设置干扰源,当干扰信号到达雷达接收机时,与回波信号的相位相干,原理如图1所示[1]。

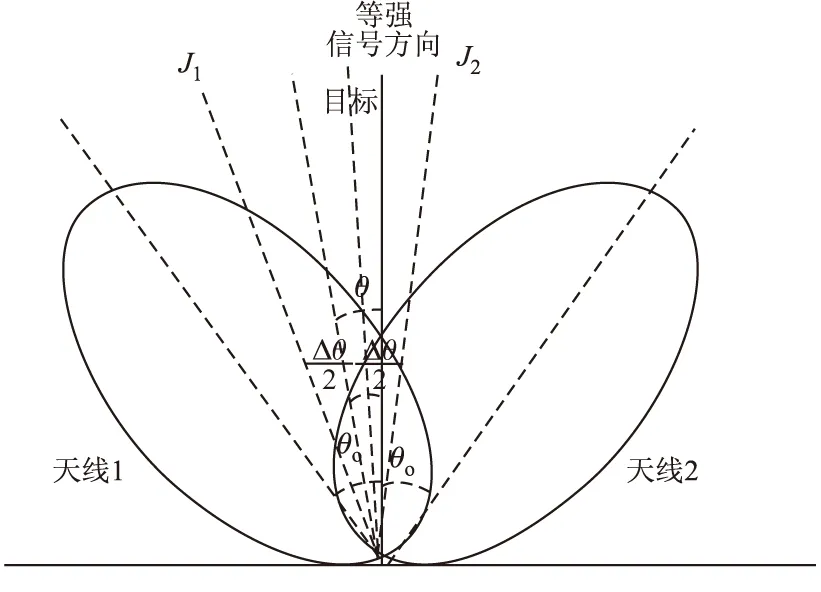
图1 相干两点源干扰原理

J1、J2分别为回波信号与干扰信号。如图1,设J1、J2在雷达天线处的相位差为Δφ,J1、J2的幅度分别为AJ1、AJ2。θ0是两波束增益最大方向和等信号方向夹角,θ是回波方向和等信号方向夹角,则J1、J2到达雷达接收天线时信号强度表达式为:

(1)

通过波束形成网络进行和差运算后,得到和信号EJΣ、差信号EJΔ分别为:

(2)

EJΣ、EJΔ分别经接收机混频、中放、相位检波等一系列处理后,输出S(t):

2AJ1AJ2cosΔφ[F(θ0-θ1)F(θ0+θ2)-

F(θ0+θ1)F(θ0-θ2)]}

(3)

式中:θ1=Δθ/2+θ,θ2=Δθ/2-θ。

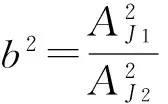
(4)

误差信号S(t)=0,则跟踪天线的指向角θ满足:

(5)

因此,相干干扰利用雷达天线口面形成相位波前失真来引起雷达指向误差,导致雷达错误跟踪。如果能够使得两路信号的相位差接近180°,两路信号将在空间形成干涉,此时式(5)中分母最大,可以使波束产生较大的偏差,从而增大单脉冲雷达的角跟踪误差,使它不能满足瞄准的要求。

2 基于散射特性的相干干扰方法

由式(5)可知,相干两点源干扰在原理上完全可行。但实际上对于复杂目标,其信号回波是雷达发射信号经过目标复杂的散射函数调制后的结果,其到达天线口面时的信号相位很难与基于点源产生的干扰信号保持相干。因此,干扰机侦测到导引头的入射信号时,应先与目标散射特性进行匹配调制。

2.1 目标散射特性建模仿真

理论计算和实验测量证明[6],在高频区,目标总的电磁散射可认为是某些局部位置上电磁散射的合成,这些局部的散射源即多散射中心。给定工作频率及姿态角情况下,可以利用多散射点模型来描述目标散射特性。文中根据目标三维CAD模型,利用电磁计算软件FEKO建立其全姿态角一维距离像模板库,在此基础上重构多散射点模型。

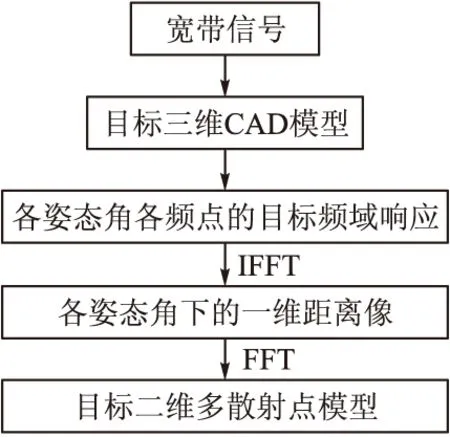
图2 目标散射函数建模仿真流程

如图2所示,在每个姿态角下用宽带信号对目标进行照射,利用FEKO算得该频域内不同频点的目标响应,然后利用逆傅里叶变换获得该姿态角下的一维距离像。由散射理论可知,当姿态角变化较大时,会发生遮蔽和散射点游动等现象,故需对目标建立不同姿态角小角区内的散射函数模型,以保证模型相对于姿态角的一致性。文中在以某目标0°俯仰角下的二维多散射点模型建立为例:首先,采用140 MHz的宽带信号(中心频率17.0 GHz),对目标进行方位角维度全360°的照射,角度间隔0.01°,建立一维距离像模板库;随后,以2.55°为间隔将方位角划分为多个小角区,在每个小角区内利用目标相应的256个一维距离像模板,借鉴ISAR的距离多普勒成像方法进行傅里叶变换,重构目标各小角区内的二维多散射点模型。图3给出了某目标方位角为1°时的一维高分辨距离像及该目标在0°～2.55°角区内的二维多散射点模型。

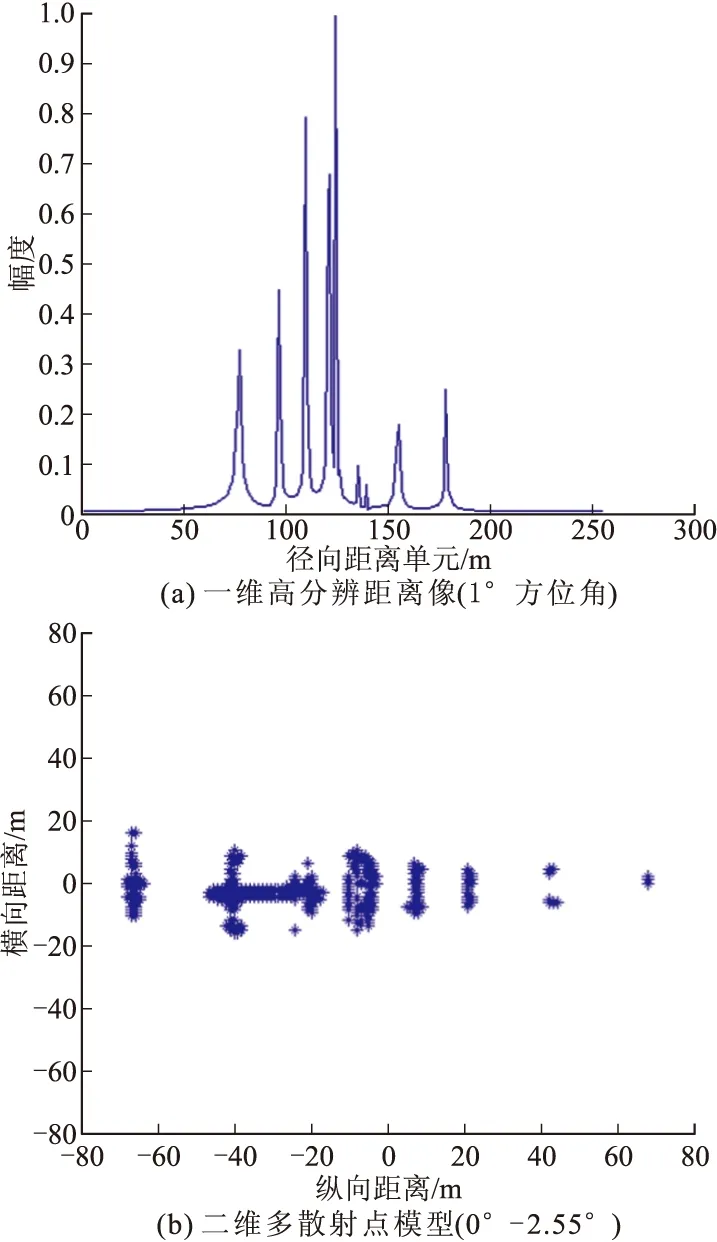
图3 某目标一维高分辨距离像(1°方位角)及二维多散射点模型(0°～2.55°方位角)

2.2 基于散射特性的相干干扰生成流程

图4给出了基于散射特性的单脉冲角跟踪雷达相干干扰生成流程。

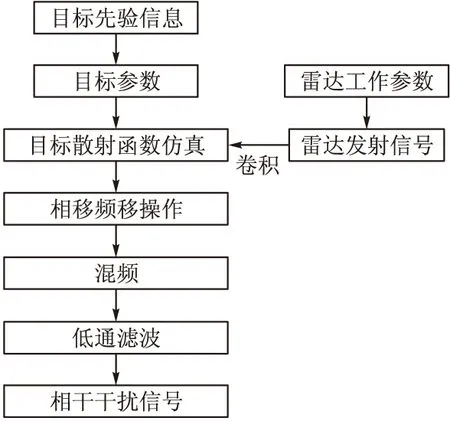
图4 基于散射特性的单脉冲角跟踪雷达相干干扰生成流程

为完整产生含有目标散射信息的相干干扰信号,需要多种因素配合,主要包括:

1)目标散射特性特征,即目标散射函数的提取和建模,以用于卷积运算;

2)我方电子支援系统所接收到的雷达发射信号或者所侦察到的雷达发射信号参数,以用于信号重构;

3)卷积操作,将重构出的雷达发射信号与目标散射函数模型进行卷积,以保证干扰信号中保留目标散射特性;

4)卷积操作完成后,须按指向角误差计算公式来附加相移、频移,以为达到相干干扰的效果;

5)通过混频等操作,将干扰信号调制到发射信号载频,并发射出去。

3 单脉冲角跟踪末制导雷达仿真平台

由于测角快,精度高,单脉冲角跟踪雷达在导弹末制导雷达中获得了广泛应用。为了验证和对比各干扰方法对单脉冲角跟踪雷达的干扰效果,文中结合实际应用场景,在单脉冲角跟踪末制导雷达仿真平台[8]上复现雷达从信号发射、传输、接收、接收机处理、信号处理、数据处理、输出制导信息的全过程;并通过弹道解算,实现与导弹制导控制系统的闭环仿真,以便观察各因素对导弹制导误差的影响,为评估干扰方法对导弹作战效能的对抗效果提供决策依据和平台支撑。

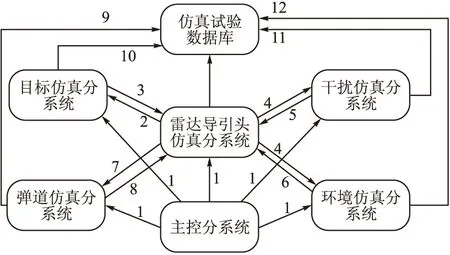
图5 仿真系统构成框图及信息交互关系

整个仿真系统由主控、末制导雷达仿真、弹道仿真、目标仿真、干扰仿真、环境仿真、仿真试验数据库等7个分系统构成,见图5。其中,雷达导引头、弹道、目标、干扰和环境5个模块通过建立相应的信息处理流程,实现仿真解算,完整地实现干扰对抗条件下的六自由度弹道仿真。完成参数设置后,将导弹和目标运动数据送入雷达导引头分系统中的接收机模型,通过该分系统中的天线模型、目标仿真分系统中的散射模型引入的遮挡损耗,相对运动引入的多普勒频移以及距离变化引入的电波传播时间差综合计算接收机输出的回波信号,随后将信号送入窄带滤波器进一步处理,以提取频谱的中心谱线,通过杂波对消和后续多普勒滤波处理在速度域形成闭环速度跟踪。利用单脉冲测角原理来提取指向误差,即框架角误差,这些误差信号送入跟踪滤波器。寻的制导通过修正比例制导律完成。导引头的相对运动状态估计送入弹道仿真分系统,弹道控制单元生成的舵偏角指令可以引导导弹向指定目标寻的,弹道解算分系统响应导引头输出的制导指令,进行弹道解算,实时地输出运动状态数据,进而完成闭环仿真全过程。表1给出了各分系统之间的信息交互关系。

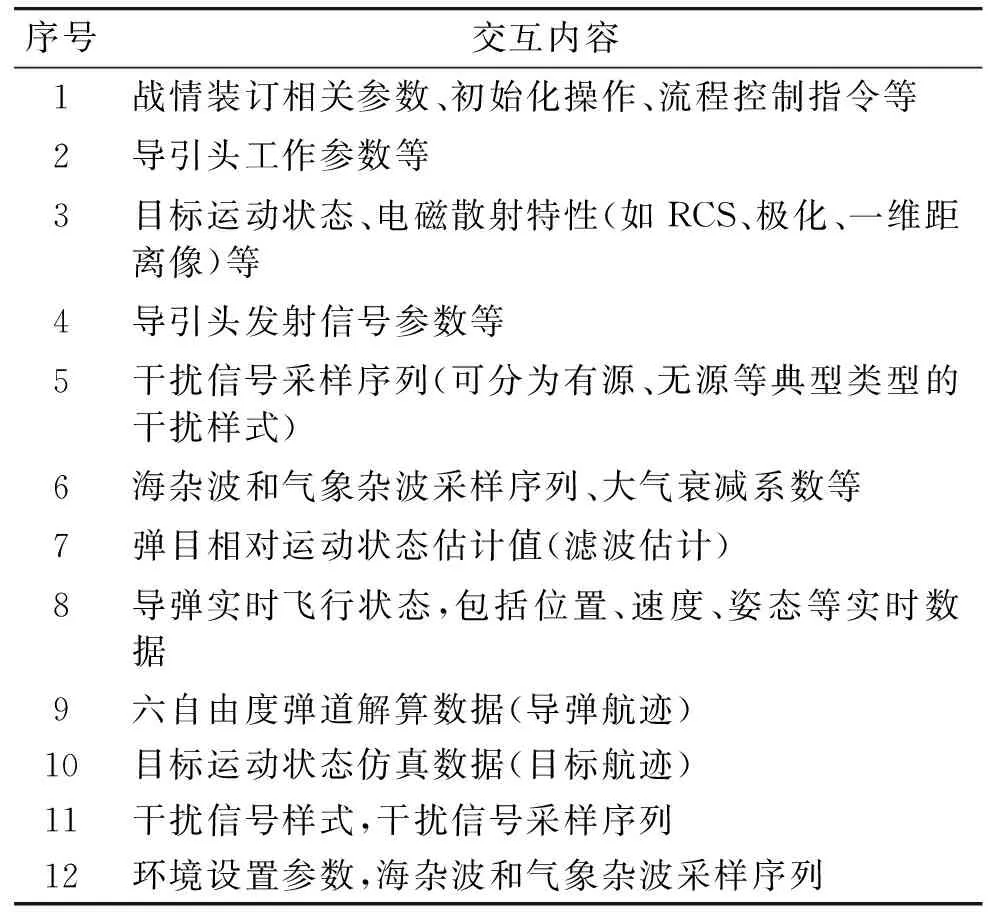
表1 仿真系统各分系统信息交互关系一览表

4 干扰方法对比验证仿真实验

在单脉冲末制导雷达仿真平台上,考虑基于点目标模型的相干干扰场景及基于散射特性的相干干扰场景进行干扰对抗的对比验证仿真实验。末制导雷达采用脉冲多普勒体制,工作载波频率17.4 GHz,脉冲宽度2.0 μs,平均发射功率300 W,发射综合损耗1.8 dB,接收综合损耗3.2 dB,大气传输综合损耗值1.0 dB,接收机热噪声系数6.8 dB,最大工作距离35 km;信号采用准连续波波形,相参处理子脉冲数512,接收机中频频率5 MHz,重频为280 kHz,系统采样频率20 MHz,工作帧周期40 ms。导弹在发射坐标系内的初始位置(0,200 m,-400 m),初始速度矢量为(400 m/s,0,0),初始航向角、俯仰角和滚动角均为0°,加速度矢量为(0,0,0),角速度矢量为(0,0,0)。目标在发射系内的目标初始位置为(7 000 m,0,0);目标舰船长度130 m,角闪烁系数取为0.35。弹体初始质量为1 030 kg,推力为6 350 N,滚动、方位、俯仰通道的转动惯量分别为56.7 kg·m2,3 996 kg·m2,3 983 kg·m2,制导律计算环节中的滞后时间常数为0.2 s,自动驾驶仪环节中的滞后时间常数为0.03 s,比例导引系数5.0,弹道解算积分步长1 ms。

相干干扰对抗仿真实验相关参数见表2。

表2 基于点目标模型的相干干扰参数设定

基于散射特性的相干干扰实验干扰相关参数与点目标模型相干干扰条件下基本相同,不同之处在于干扰信号生成流程按照图4所示的干扰信号生成流程执行。

图6给出了基于点目标模型的相干干扰下的导引头方位、俯仰框架误差角提取曲线测量值与真实值之间的比对。

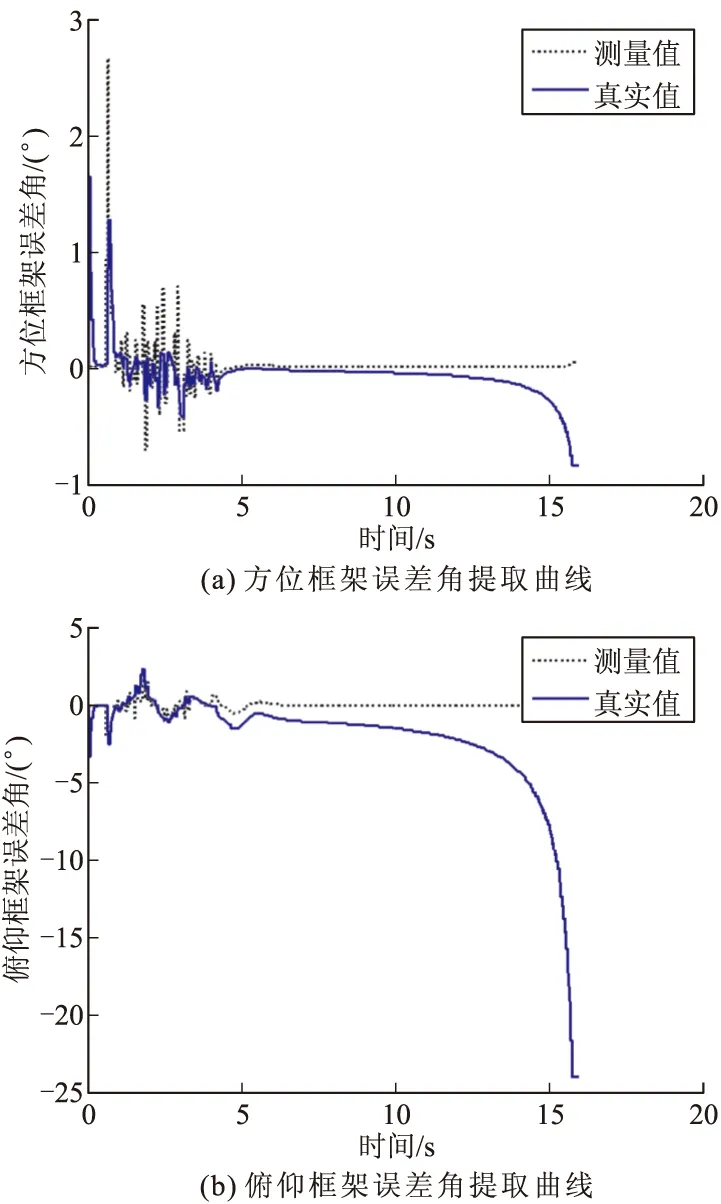
图6 基于点目标模型的相干干扰下的导引头框架误差角提取曲线

图7给出了基于散射特性的相干干扰下的末制导雷达方位、俯仰框架误差角提取曲线测量值与真实值之间的比对。

图8分别给出了基于点目标模型的相干干扰下及基于散射特性的相干干扰下发射系内的全弹道飞行航迹图,即三维攻防对抗态势图。发射系的定义是以发射点为坐标圆心的当地北天东地理坐标系,从图中可清晰地看出导弹的飞行航迹。在基于点目标模型的相干干扰下,导弹最终脱靶量为78.5 m;而在基于散射特性的相干干扰下,导弹最终脱靶量为146.3 m。

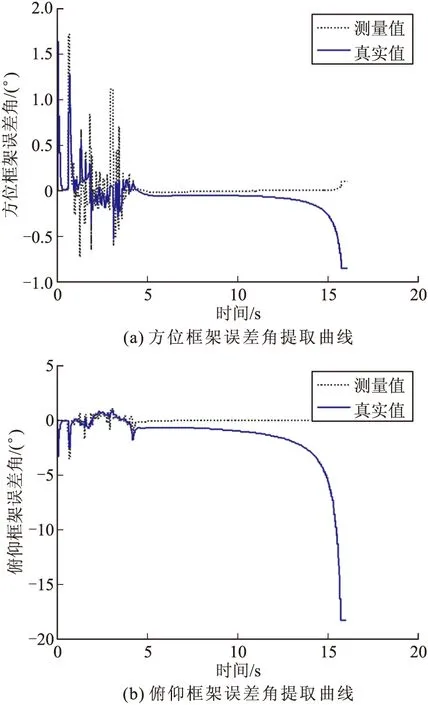
图7 基于散射特性的相干干扰下的导引头框架误差角提取曲线

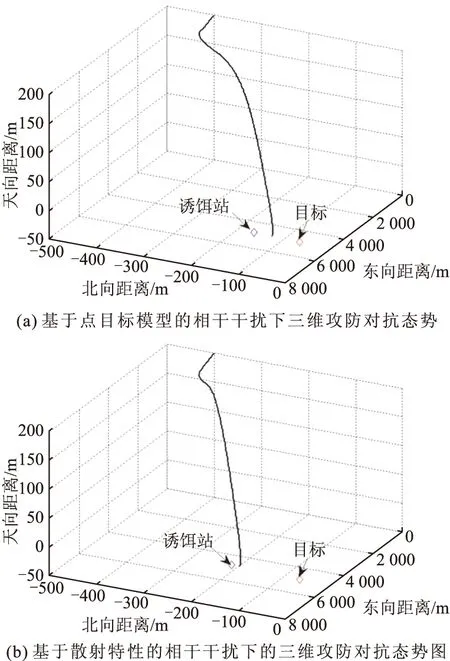
图8 两种相干干扰下的三维攻防对抗态势图

由图7、图8可以看出,当采用基于点目标模型的相干干扰方法时,具有一定的干扰效果,但脱靶量与目标尺寸相比不够大,仍有可能对目标造成毁伤。当通过目标多散射点模型来近似目标散射函数,以生成PD导引头相干干扰信号时,实施干扰后,方位框架误差角在3～5 s处出现震荡的力度更大,诱偏效果比基于点目标模型的相干干扰有所提高。从脱靶量与目标尺寸的比较来看,在采用基于散射特性的相干干扰方法的情况下,导弹命中点能够被有效诱骗至目标尺寸之外。

5 结束语

从仿真实验中可看出,当通过目标多散射点模型来近似目标散射函数生成PD导引头相干干扰信号,能够达到较好的诱骗效果,理论上具有可行性,具体的诱骗距离与散射模型精度及相干干扰参数设置均密切相关,可借助末制导雷达系统仿真平台进行多次闭环仿真,以便定量分析各干扰参数对导引头的影响效应,为实际作战提供依据与指导。实际作战中,受系统精度和导弹、目标、干扰机平台位置关系等各种误差源因素影响,形成精确的相干干扰信号非常困难。今后,将进一步研究目标散射函数的精确仿真、时间同步及相位控制技术以及相位误差对相干干扰效果的影响。

[1] 陈安娜. 对单脉冲雷达的相干两点源干扰机理研究 [J]. 航空兵器, 2007(2): 7-11.

[2] 张曦, 王星, 王红卫, 等. 单脉冲雷达的相干干扰研究 [J]. 现代雷达, 2013, 35(12): 21-25.

[3] 李相平, 赵腊, 胡磊. 相干两点源对反舰导弹导引头的干扰研究 [J]. 制导与引信, 2008, 29(3): 48-52.

[4] JIA Z S, SI X C. Analysis on the tracking performance of active radar seeker under the condition of coherent interference [C]∥ IEEE International Conference on Intelligent Computing and Intelligent Systems, 2009: 418-422.

[5] 张仕山, 靳学明. 一种SAR相干干扰信号产生快速算法 [J]. 电子学报, 2009, 37(1): 108-111.

[6] 安红, 杨莉. 脉冲多普勒雷达导引头仿真研究 [J]. 中国电子科学研究院学报, 2009, 4(6): 624-629.

[7] 焦彦华. 主被动复合制导雷达性能评估研究 [D]. 长沙: 国防科学技术大学, 2004.

[8] 王阳. 主被动复合雷达导引头抗噪声干扰仿真评估 [D]. 长沙: 国防科学技术大学, 2011.

[9] 莫翠琼, 李加海, 戴幻尧, 等. 速度欺骗干扰对反舰PD导引头的相干视频仿真 [J]. 系统仿真学报, 2015, 27(5): 1024-1029.

[10] 莫翠琼, 陈秋菊, 戴幻尧. 反舰导弹雷达导引头舰船目标回波仿真技术 [J]. 计算机仿真, 2014, 31(10): 16-19.

Coherent Jamming Method of Mono-pulse Angle Tracking Radar Based on Scattering Function

CHEN Qiuju1,MO Cuiqiong1,SUN Jie1,DAI Huanyao2

(1 Electronic Engineering Institute, Hefei 230037, China;2 Luoyang Electronic Equipment Testing Center, Henan Luoyang 471003, China)

In coherent dual point-source jamming, it’s not suitable to use a particle model for simulation of a target if the target’s scattering function is complex, so a coherent jamming method based on scattering function of complex target was developed. Jamming signals are obtained from radar-transmitting signals modulated with the scattering function to be coherent with echoes. In view of evaluation of the jamming effect, the mono-pulsed angle tracking PD seeker is taken as an example to be analyzed in six degree-of-freedom trajectory simulation in the closed loop (PDRS). The results of the verification tests could provide an effective and practical solution for parameters design and performance evaluation of tactical cruise missile.

coherent jamming; mono-pulse angle tracking radar; target scattering characteristics; signal simulation

2015-06-23

陈秋菊(1982-),女,江苏如东人,讲师,博士研究生,研究方向:雷达对抗与雷达信号处理。

TN974

A