基于灰色层次分析法-BP神经网络的数据链系统效能评估*

陈 强,陈长兴,陈 婷,程蒙江川

(1 空军工程大学理学院,西安 710051;2 西安邮电大学,西安 710051)



基于灰色层次分析法-BP神经网络的数据链系统效能评估*

陈 强1,陈长兴1,陈 婷2,程蒙江川1

(1 空军工程大学理学院,西安 710051;2 西安邮电大学,西安 710051)

为进一步提高效能评估的可信性及智能化水平,提出了一种基于灰色AHP理论的数据链系统BP神经网络效能评估模型。从数据链系统性能结构出发,针对数据链信息优势的特点,建立了数据链系统作战效能评估指标体系。通过专家组依据标准打分的方式,采用AHP确定指标的权重向量,考虑借助灰色理论白化指标,最后与不同灰类分效能值聚合生成综合效能评价值从而建立了效能输出模型。构造三层BP神经网络模型,以专家的知识与经验作为输入,以灰色AHP综合效能评价值作为输出训练网络。最后通过实例验证,由于该模型运用BP神经网络非线性拟合的优势继承并有效聚合了专家的知识与经验,结果与专家评定一致,从而论证了模型的有效性及可靠性,为数据链系统效能评估提供了智能化的算子,在数据链的发展和应用中发挥重要作用。

数据链系统;指标体系;灰色系统理论;层次分析法;BP神经网络

0 引言

数据链系统是指一种能够按照统一的数据格式和约定的通信协议,通过有线或者无线信道(以无线信道为主)对格式化信息进行实时、可靠、安全、保密传输的数据通信与处理系统[1]。数据链系统的应用,使独立的作战单元相互“铰链”、“耦合”,各作战单元彼此构成一个数据通信网络,同时还可以对接收到的各种有效信息(本作战单元的传感器信息及目标威胁信息以及从其他作战单元接收的信息)进行(融合)处理,在一定程度上实现大量信息共享、高效实时的战场指挥、实时精确的武器协同、态势共享等功能[1-2]。数据链系统在现代信息化条件下的战场上扮演了愈发重要的角色,是现代信息战争的“倍增器”,

因此研究数据链系统的效能评估将对数据链装备的发展和应用起到极大的推进作用。

灰色系统理论实现了不确定性系统在信息贫乏条件下由“灰”生成“白”,从而很好的提高系统指标量化的准确性和可信度。而层次分析法通过定量分析与定性分析相结合的方式解决了层级之间、指标之间权重问题。二者的结合为效能评估提供了新思路,同时克服了专家主观性及最大限度的利用专家的评判结果,使评估结果更为准确和可信。

现有文献中,大多集中在利用评估理论和方法支撑指标到效能的数据对应关系,造成评估过程繁琐结果缺乏可信性。在文献[3]倚靠BP(back propagation)神经网络的非线性拟合能力很好的解决了评估指标到效能值的映射问题,但网络训练以“灰色”贫样本的专家打分值作为输出值其结果显然缺乏可信度和准确性。文献[4]从系统内部权重因子耦合出发,引用经典理论分层分析法(analytic hierarchy process,AHP)来构造BP神经网络训练样本,有一定的借鉴意义。文献[5]吸收灰色系统理论指标评判“漂白”的优点,评价值具有一定的可信性和准确性。文献[6]聚合灰色理论的“漂白”功效及AHP的权重耦合特性,具有理论借鉴意义,但文中过程较为复杂,亟待在继承专家经验和知识的基础上简化指标到效能的映射过程。

文中在灰色层析分析法的基础上利用BP神经网络的非线性拟合能力,以白化的专家评判值作为输入,以灰色AHP评估结果作为输出,从而合理的继承了专家的知识与经验,为数据链系统评估提供了算子化的思路。

1 基本思路

1)建立系统指标体系H递阶层次结构;

2)利用层次分析法确定指标权重ω及ωi,再运用灰色系统理论白化指标向量进而求解最大限度地包含专家水平与经验的评判值;

3)构建BP神经网络评估模型结构;

4)选取经过白化的专家评分输入样本及灰色AHP评估结果输出样本,训练网络直至满足精度。

具体流程如图1所示。

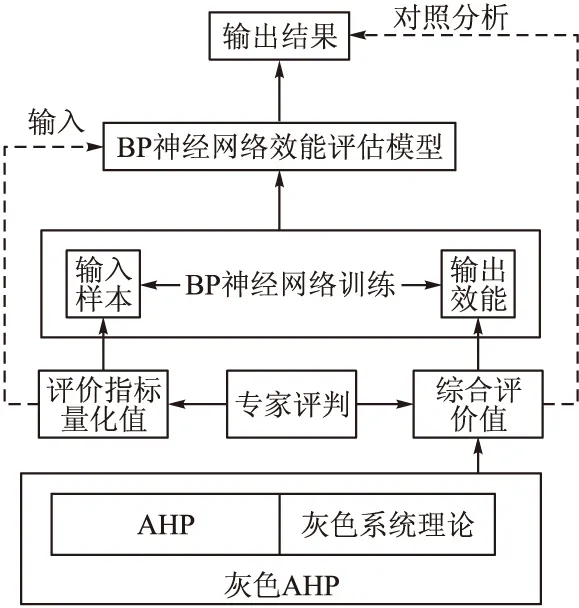
图1 灰色AHP-BP神经网络评估模型

2 数据链系统作战效能评估指标体系

数据链系统作战效能评估指标体系的构建必须遵循系统性原则、可比性原则、定性和定量相结合原则、独立性原则、层次性原则和客观性原则,同时又要考虑到影响数据链系统作战能力影响因素比较多的特点[5]。在分析数据链系统功能、结构和特点的基础上,根据数据链信息传递的实时性、信息处理的可靠性、安全保密及交互战术信息的要求,文中从信息处理能力、信息传输能力、网络管理能力、信息安全防护能力、可用性及可信性六个方面来分析数据链系统的效能,建立了如图2所示的数据链系统作战效能评估指标体系[6]。

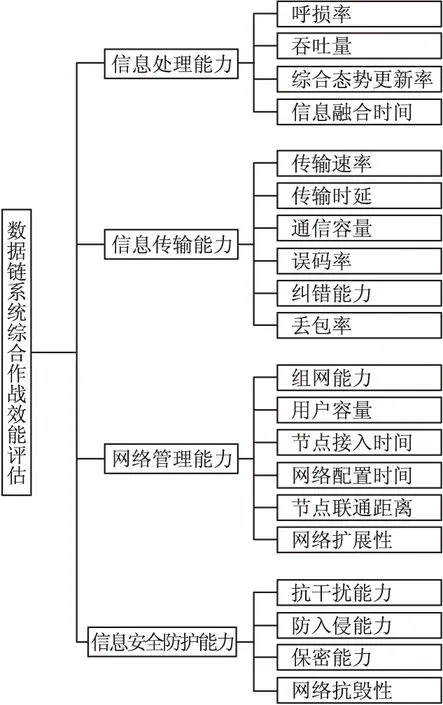
图2 数据链系统效能评估指标体系

3 灰色AHP模型的建立

3.1 评价指标权重的确定

依据层次分析法的基本原理,在已构建的指标体系的基础上,选取相关领域专家参照1-9标度针对各层元素关于准则层的重要性进行两两比较从而形成判断矩阵。这里采用和积法来计算生成的判断矩阵A的最大特征值λmax及特征向量ωi,即为指标层评价指标hij的相对权重并同样记为ωi,其中一级指标相对权重记为W,具体运算步骤如下:

1)将矩阵A中元素按列分别归一化,即求得:

(1)

2)将归一化矩阵按行分别相加,即:

(2)

3)将wij按列归一化即得权重向量,即:

(3)

4)计算矩阵A的最大特征根,记为:

(4)

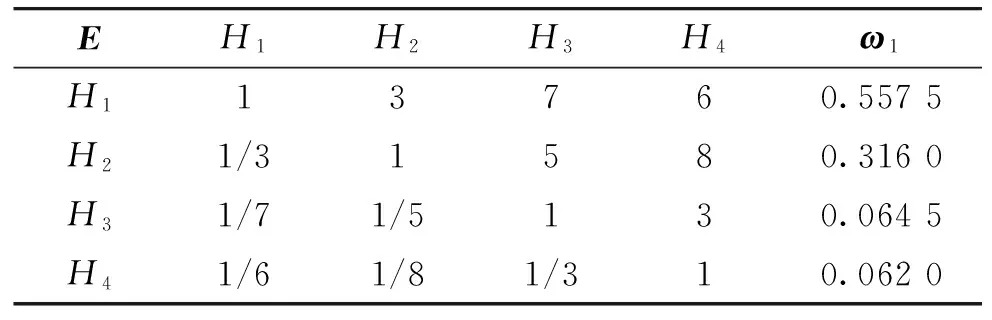
表1 系统效能H1的判断矩阵及权重向量ω1

3.2 构造评价指标样本矩阵

将指标评分等级划分为4类,分别对应优、良、中、差4个评分标准,对应分值分别为4、3、2、1分,考虑到评判过程中出现的模糊类别,细化增加了3个中间等级标准,赋值分别为3.5、2.5、1.5分。

依据以上评分标准,遴选了n位专家分别对某型数据链系统各评价指标评判打分,制作了如表1所示的按递阶层次结构给出的评分表,依据指标优劣分别在发放的评分表中给出对应分值。

综合n位专家的评分结果得到某型数据链系统的评估样本矩阵:

其中:i=4,j=25,hijl表示第l位专家对指标hij的评分值。

3.3 确定评估灰类

评估灰类涉及的3个重要属性分别是评估灰类的等级数、灰类的灰数及灰类的白化权函数[6],三者的确定是关键。根据指标评分等级标准设定4个评估灰类,即e=1,2,3,4,分别对应优、良、中、差4个等级,相应的白化权函数依次为:

1)第一灰类“优”(e=1),灰数设定为⊗∈[4,+∞),其对应的白化权函数为f1,如图3所示;

2)第二灰类“良”(e=2),灰数设定为⊗∈[0,3,6),其对应的白化权函数为f2,如图4所示;

3)第三灰类“中”(e=3),灰数设定为⊗∈[0,2,4),其对应的白化权函数为f3,如图5所示;

4)第四灰类“差”(e=4),灰数设定为⊗∈[4,∞),其对应的白化权函数为f4,如图6所示。

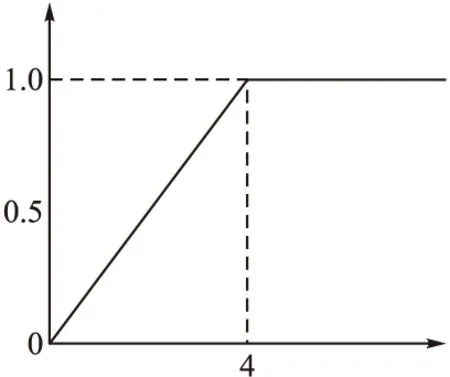
图3 第一灰类

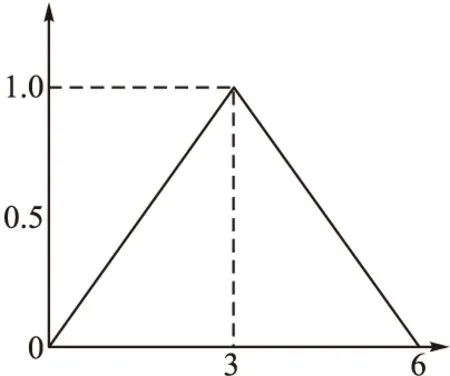
图4 第二灰类

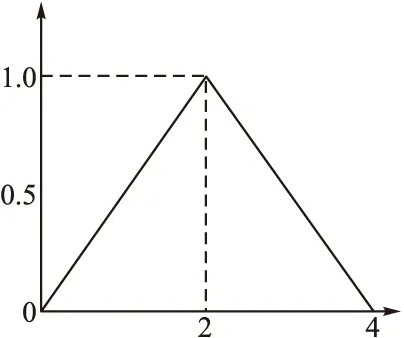
图5 第三灰类

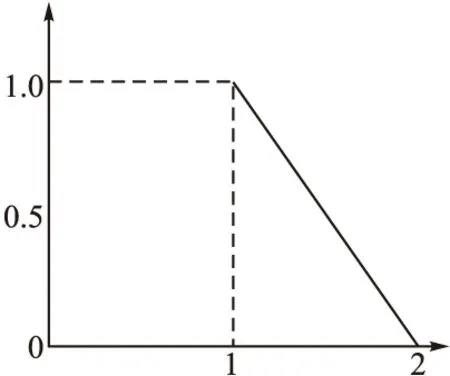
图6 第四灰类

3.4 计算灰色评价权重及构造灰色评价矩阵

对于数据链系统指标Hi对应的二级指标层评价指标hij,将n位专家评判打分值依次代入e(e=1,2,3,4)灰类相应的白化权函数得e灰类灰色评估系数,记为xije,总评估系数记为xij,具体数学表达式为:

则e灰类的灰色评价权系数为:

rije=Qije/Qij

由以上关系,容易得出数据链系统底层指标hij对于4个等级灰类的灰色评价矩阵Ri为:

3.5 计算数据链系统作战效能的综合评估值

1)将灰色评估权矩阵Ri与数据链系统评价指标Hi对应二级指标hij的相对权重结合,得到综合效能评估值,记为Di,即:

2)由评价指标Hi的综合评估效能值Di聚合得到系统一级指标H总的灰色评估矩阵R。

据此可以求出数据链系统总的灰色评估结果D为:

D=ωT·R=[d1,d2,…,d5]

3)将四灰类依据等级标准赋予不同的分效能值,其组成的分效能向量设定为C=[9,7,5,3],以此对总的灰色评估矩阵进行归一化处理,得到数据链系统作战效能评估值E为:

E=D·CT=[d1,d2,…,d5]·[9,7,5,3]T

数据链系统综合评估效能值即为所求。

依据上述理论及计算方法,考虑各指标等级划分及对应量化赋值不同,可将综合评价值按标准划分为4个档次。当专家对指标Hij一致评定为4分时,得到的综合评价值为E=8.200;评定一致为3.5分时E=7.638 3;评定一致为3分时E=7.222;评定一致为2.5分时E=6.886 8;评定一致为2分时E=6.538 3;评定一致为1分时E=4.840。从而根据综合评价值区间等级分类如表2所示。

表2 5个分类等级评估值区间

4 灰色AHP-BP神经网络评估模型的实现

BP神经网络的非线性逼近能力对于解决数据链系统效能评估问题提供了一个新的思路[4,6],为系统效能评估设计了算子化的模型。文中采用典型的三层BP神经网络模型,即包含输入层、隐含层及输出层[3]。具体结构如图7所示。其中输入层神经元节

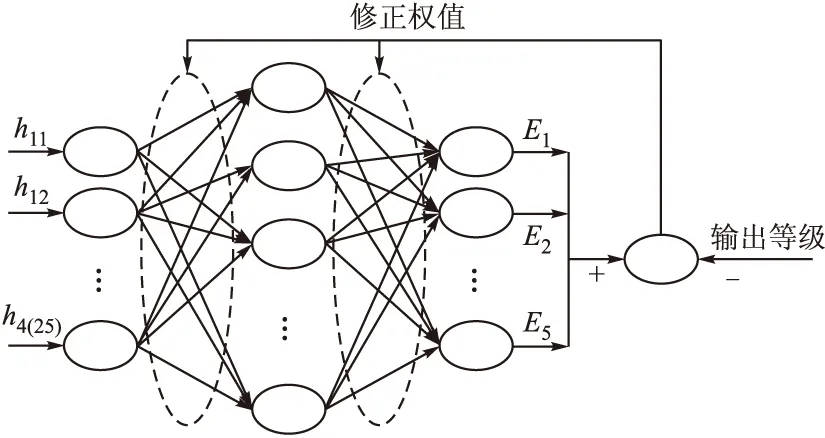
图7 BP神经网络结构示意图

其中隐含层激活函数f设置为S型函数:

4.1 选取训练样本

训练样本的选取对网络的性能至关重要,关系着效能评估的可信性和准确性。文中从这两点出发,选取10位专家分别依次对各指标评判打分,抽取灰色层次分析法白化指标作为输入值,灰色层次分析法评估值作为输出值作为原始训练样本。具体数据如表3所示(由于篇幅限制仅截取部分样本值)。

表3 专家评判打分及综合评估值

4.2 网络训练及仿真学习

将上述样本值用于对网络进行训练,直到满足设定的精度要求才结束。部分网络性能参数设置如下:

net.trainParam.epochs=7 000;

%设置网络训练次数

net.trainParam.show=100;

%设置显示间隔的训练次数

net.trainParam.mc=0.09;

%设置附加动量常数

net.trainParam.goal=1e-50;

%设置允许误差范围

net.trainParam.lr=0.15;

%设置网络学习速率

网络训练的误差曲线如图8所示,当学习到100次时训练结束,表明网络已经满足了误差精度要求,此时BP神经网络已建立了从专家评价到系统效能等级评价的映射。

为了验证BP神经网络评估模型的准确性及实用性,以某型数据链系统为例,以专家依据等级评价作为输入送到训练好的网络中,输出结果与专家总体评价进行对比分析。结果如表4所示。显然从表4中容易得到神经网络输出值与专家总体评价吻合,同时结合灰色层次分析法结果进行对照分析结论一致,从上述结果可以得出BP神经网络数据链系统评估模型结构合理,结果比较理想,可以用于数据链系统的效能评估,进一步为数据链系统的应用提供了理论参考及智能化的评估,具有一定的应用价值,也为评估方法和理论开辟了一个新的方向和创新点。

表4 仿真结果对照分析表

图8 误差曲线图

5 结束语

针对数据链性能特点及信息优势建立数据链系统效能评估指标体系,并采用基于灰色AHP-BP神经网络的评估方法。首先构建灰色AHP模型建立从专家评判值到效能评价值的输出模型,以此采集网络输入输出样本,接下来采用BP神经网络非线性拟合能力把体现专家知识与经验的等级评分值映射到系统效能,最后通过实例分析结果理想可靠,为评估理论指明了一个新的方向。文中也只是在贫样本环境下训练网络,下一步将结合其他优化算法进行探索研究,考虑拟和能力更强的优化算法在大样本训练条件下评估的准确性。

[1] 潘寒尽, 张德和, 邱学军. 基于模糊灰色理论的数据链系统作战效能评估 [J]. 现代防御技术, 2001, 39(4): 60-64.

[2] 吕娜. 数据链理论与系统 [M]. 电子工业出版社, 2011: 36-40.

[3] 周燕, 陈烺中, 李为民. 基于BP神经网络的弹炮结合系统作战效能评估 [J]. 系统工程与电子技术, 2005, 27(1): 84-86.

[4] 陈佳昀, 武斌, 唐唐. AHP和BP神经网络在通信效能评估中的应用 [J]. 现代电子技术, 2009, 25(7): 65-67.

[5] 潘寒尽, 张德和, 邱学军. 基于模糊灰色理论的数据链系统作战效能评估 [J]. 现代防御技术, 2011, 39(4): 60-64.

[6] 陈士涛, 张志峰, 归建洲. 基于灰色理论的电子维修车保障效能综合评估 [J]. 系统工程与电子技术, 2009, 31(4): 994-996.

[7] 李志猛, 徐培德, 冉承新. 武器系统效能评估理论及应用 [M]. 北京: 国防工业出版社, 2013: 50-56.

[8] 王锐, 张安, 史兆伟. 基于幂指数法和AHP的先进战斗机效能评估 [J]. 火力与指挥控制, 2008, 33(11): 73-76.

[9] 孙继银, 付光远. 战术数据链技术与系统 [M]. 北京: 国防工业出版社, 2009: 80-95.

[10] 韩晓明, 张金哲, 张君. 基于指数法的航空装备对比优势评估模型 [J]. 系统工程与电子技术, 2009, 31(6): 1409-1414.

[11] 轩永波, 黄长强, 王勇. 基于灰色层次分析法的空间武器作战效能评估 [J]. 空军工程大学学报, 2011, 12(2): 32-37.

[12] LEE B R, JUNG E K, CHOE S. Link-16 simulator design over jamming environments and Link-16 performance analysis with or without time synchronization [J]. Telecom Reviewm, 2013, 23(2): 261-275.

Efficiency Evaluation of Data Link System Based on Gray AHP-BP Neural Network

CHEN Qiang1,CHEN Changxing1,CHEN Ting2,CHENG Mengjiangchuan1

(1 Science College, Air Force Engineering University, Xi’an 710051, China;2 Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

In order to improve the level of credibility and intelligence of efficiency evaluation, a BP neural network effectiveness evaluation frame of data link system on the basis of gray AHP theory was proposed. Considering performance and structure of data link system, according to the characteristics of advantage of data link information, the operational effectiveness assessment index system of data link was established. Through expert marking by standard, using AHP to determine the weight vectors of index, considering to use the albino indicators index of gray theory aggregate with different gray class efficiency value to generate comprehensive efficiency evaluation so that the output efficiency model was established. A three-layer BP neural network model was structured with the expert’s knowledge and experience as input, and the grey AHP comprehensive efficiency evaluation value as the output of the training network. Finally, the experiment validated that the result was consistent with the expert evaluation. Since the model uses the advantage of nonlinear fitting inheritance of BP neural network and aggregates the expert’s knowledge and experience effectively, therefore, it demonstrates validity and reliability of the model and provides intelligent operator for the data link system effectiveness evaluation. The model plays an important role in development and application of the data link.

data link system; index system; gray system model; analytic hierarchy process; BP neural network

2015-07-10

陕西省自然科学基础研究项目(2014JM8344)资助

陈强(1989-),男,江西南昌人,硕士研究生,研究方向:数据链系统效能评估及影响分析。

TN919

A