固冲发动机导弹方案弹道设计与优化*
张磊扬,孙振华,贺永杰
(中国空空导弹研究院,河南洛阳 471009)
固冲发动机导弹方案弹道设计与优化*
张磊扬,孙振华,贺永杰
(中国空空导弹研究院,河南洛阳 471009)
文中针对以固冲发动机为动力装置的导弹弹道特性与推力特性高度耦合的特点,建立了相应的方案弹道优化模型,并采用基于遗传算法与序列二次规划算法的组合优化方法,以最大射程为目标进行内外弹道一体化优化设计。弹道仿真结果表明:所得到的优化后的飞行弹道方案,在满足飞行条件约束和发动机设计约束的情况下,射程提高了约21.7%。从而验证了所用优化方法的有效性以及一体化优化设计的必要性。
固冲发动机;方案弹道;一体化设计;优化
0 引言
随着现代武器技术的进步及作战模式的发展,传统的火箭发动机已难以满足现代空战对机载武器动力装置的需求。固体火箭冲压发动机(以下简称“固冲发动机”)具有结构简单、工作可靠、维护使用方便及推力可调节等优点,在相同的体积和质量条件下,能够提供比常规火箭发动机更多的能量,从而显著增加导弹的射程和机动性能。这对于体积和质量约束较为严格的机载导弹来说更具吸引力,因此高性能可变流量固冲发动机是远程机载导弹首选的动力装置[1]。
以固冲发动机作为动力装置的导弹弹道特性与发动机特性具有强耦合性。一方面,固冲发动机的性能指标(推力、比冲)随着导弹外弹道参数(高度、速度、攻角等)及实际进入发动机的空气流量的变化有明显变化;另一方面,固冲发动机的工作特性将直接影响导弹的飞行性能。因此在固冲发动机导弹的弹道设计过程中,必须考虑在各种约束条件下,将弹道特性与固冲发动机特性结合起来进行优化[2-3]。
1 弹道计算模型
1.1 飞行方案弹道设计
以机载方式发射的固冲发动机为动力的导弹,经过助推器助推至转级马赫数后固冲发动机开始工作,并继续加速爬升至巡航高度,并在巡航马赫数下开始等马赫数巡航飞行,接近目标后,对目标进行俯冲攻击。导弹弹道由助推段加速、最优爬升段、平飞巡航段以及俯冲攻击段构成。具体过程如图1所示。
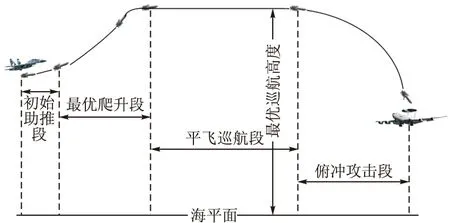
图1 固冲发动机导弹方案弹道示意图
1.2 弹道假设条件及飞行力学方程
为了研究方便,采用以下假设:1)将导弹看作可控质点,仅研究导弹在垂直平面内的运动;2)导弹控
制系统理想的工作,既无误差,也无延迟,忽略随机干扰影响;3)不考虑地球曲率和自转的影响。
基于上述假设,导弹的运动方程组如下所示[4]:
(1)
式中:V为导弹速度;P为推力;m为导弹质量;α、θ分别为攻角和弹道倾角;x、y为水平距离和高度;X、Y分别为气动阻力和升力,分别由以下公式求得:
(2)
式中:ρ为大气密度;AR为参考面积;CX和CY分别为气动阻力系数和升力系数,可通过对应马赫数和攻角进行插值求得。
2.3 控制规律模型
对于铅垂平面内的方案飞行来说,可采用给定弹道倾角、俯仰角、攻角、高度、法向过载等的控制规律而实现。对于使用固冲发动机的导弹来说,为了保证固冲发动机能够正常工作,需要将攻角限制在一定范围内,但由于目前测量导弹攻角的传感器精度比较低,所以一般不直接采用控制导弹攻角参数,而是将其折算成俯仰角,通过对俯仰角的控制来实现对攻角的控制。因此,文中选用给定俯仰角指令作为导弹的控制规律。由于爬升到巡航高度后要进行等高飞行,可将爬升段和巡航段的控制规律一起设计。为了获得合适的爬升快速性和较小的高度超调,将俯仰角指令设计成高度差和垂直速度变化的函数。经过仿真确定冲压发动机工作期间的俯仰角ϑ指令控制规律如下:
对于爬升/巡航段:
ϑ=ϑ0+k1(H-Hc)+k2Vsinθ
(3)
式中:ϑ0为导弹能够进行等高飞行所能维持的常值俯仰角;Hc为指定的巡航高度。
对于俯冲下降段:
ϑ=ϑ*+k3(H-Hc)
(4)
式中ϑ*表示为使导弹从巡航段转入俯冲下降段所预先设定的常值俯仰角。
1.4 导弹质量模型
导弹在整个工作过程中质量是逐渐减少的。在助推段,可以近似按等质量流率计算,在固冲发动机工作阶段,其质量流率与飞行性能参数有关。导弹质量的变化规律(考虑转级装置质量)如下:
(5)
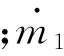
2.5 发动机推力计算模型
导弹发射后,需要使用助推发动机加速至接力马赫数后,固冲发动机才能开始正常工作,因此,导弹飞行过程中发动机提供的推力由助推发动机工作段推力和固冲发动机工作段推力组成[5]。
在弹道设计中,为简化计算,可近似认为助推段燃气流量恒定,产生的推力为一定值。固冲发动机推力的计算与分析过程使用基于等熵流动的一维计算模型,具体可见参考文献[6]。经过进行仿真分析,可得到发动机推力P的变化规律为:
(6)
式中:Pboost为助推发动机推力,Ma为飞行马赫数;αg为余气系数。
2 优化模型
2.1 设计变量选取
优化设计变量是指飞行弹道设计方案中对于目标影响较为显著,并具有关键作用的参数变量。基于上述章节所述的飞行弹道方案,结合固冲发动机性能计算模型以及飞行力学方程,根据优化目标和设计经验,选择以下参数作为设计变量:
1)爬升/巡航段控制规律参数k1、k2;
2)俯冲下降段控制规律参数k3;
3)巡航高度Hc;
4)巡航马赫数Mac;
5)固冲发动机补燃室喉部直径Dt;
6)固冲发动机进气道捕获面积Ai。
其中,k1、k2、k3为控制参数,影响着导弹控制规律的变化;Hc和Mac为飞行弹道参数,对导弹的爬升和巡航性能有着重要影响;Dt和Ai作为固冲发动机的内弹道参数,对发动机的性能起关键作用。通过将这些参数结合起来优化,可以更好的发挥固冲发动机的性能,提升导弹的弹道性能。
2.2 约束条件
根据所设计方案弹道的特点和固冲发动机的工作需求,设定以下约束条件:
1)马赫数约束:固冲发动机只有飞行马赫数保持在一定范围内才能进行工作,因此,在导弹飞行过程中,要对固冲工作段马赫数加以约束。同时,基于目标的机动特性和导弹末制导的需求,需要使得在俯冲下降段结束时,导弹仍具有较高的末端马赫数Maend,以保证导弹在接近目标时仍具有较高的机动性能。
2)攻角约束:为保证固冲发动机正常工作,需要使得导弹攻角限制在一定范围内,即αmin≤α≤αmax。
3)冲压补燃室压强约束:在固冲发动机工作过程中,若冲压补燃室压强pb过低,燃烧效率会大幅下降,甚至有可能造成熄火,因此,需要对其进行限制。
4)进气道裕度约束:在固冲发动机工作过程中保证其大于0以避免进气道进入亚临界状态。
2.3 目标函数
工程设计中设计方案是否最优需要使用特定的准则或者指标进行评判,这种准则和指标一般使用目标函数来表示。基于一体化设计的思想[7],结合固冲发动机导弹的弹道特性和发动机特性,文中选用导弹射程作为目标函数。即:
J=xmax=f(k1,k2,k3,Hc,Mac,Dt,Ai)
(7)
2.4 优化方法
现有的优化方法可以分为两大类:基于梯度的数值优化方法和智能优化方法。在数值优化方法中,序列二次规划法(SQP)[8]是应用最为广泛的一种方法,具有收敛性好,计算效率高,局部搜索能力强的优点,但其得到的往往是局部最优解而非全局最优解。相对于数值优化方法来说,以遗传算法(GA)[9]为代表的智能优化方法具有不依赖于梯度信息,全局搜索能力强,鲁棒性好的优点,但同时也存在着收敛速度慢,计算效率低的缺点。
综合上述两种算法的互补特性,针对固冲发动机导弹方案弹道优化问题高度非线性、约束复杂、求解难度较大的特点,文中采用将遗传算法与二次序列规划法进行结合的组合优化方法。该方法的基本思想为:首先使用遗传算法进行全局寻优,判断优化空间的性质和最优解所在区间。然后在此区间内使用序列二次规划法得到满足精度要求的最优解。因而,该组合方法既具有遗传算法的良好的全局搜索能力,又具有二次序列规划法的较高的计算效率。该方法具体流程如图2所示。
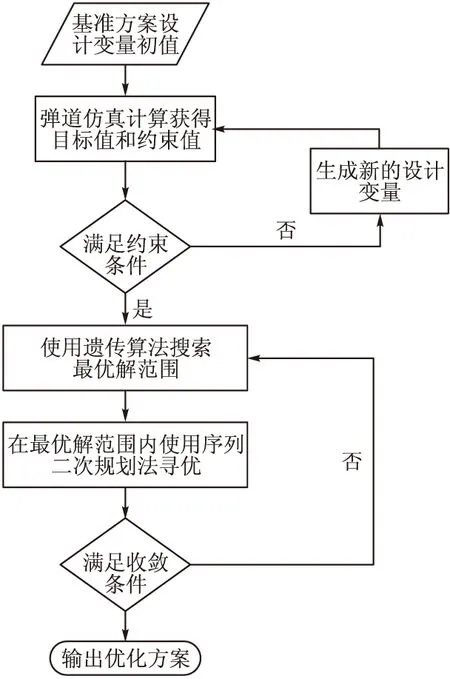
图2 组合优化方法流程图
3 算例及结果分析
3.1 仿真算例及初始条件
文中采用上述优化模型对某型固冲发动机导弹的方案弹道进行仿真计算,其中,飞行力学模型采用四阶龙格-库塔方法进行解算,其主要计算条件为:
导弹在H=15 km,Ma=1.4的初始飞行条件下发射,经过爬升-巡航-俯冲等飞行阶段后,当导弹俯冲至目标高度时结束计算。将待优化的方案弹道定为基准弹道。
3.2 优化结果及分析
采用上述优化方法经过优化计算后,得到优化后的设计变量,将其代入弹道仿真程序中,可以得到相应的性能参数。以基准弹道各参数值作为参考,经过无量纲化处理后,对应的设计变量与基准方案弹道对比如表1所示。
从表1可以看出,优化之后虽然飞行时间有所增加,但末端马赫数与基准方案基本一致,保证了战术技术的需求。与此同时,在满足各种约束条件的前提下,优化方案的射程比基准方案增加了约21.7%,增程效果显著。
图3~图7给出了基准方案以及优化方案进行弹道仿真后的弹道曲线及各性能参数的变化曲线(图中数据均经过无量纲化):
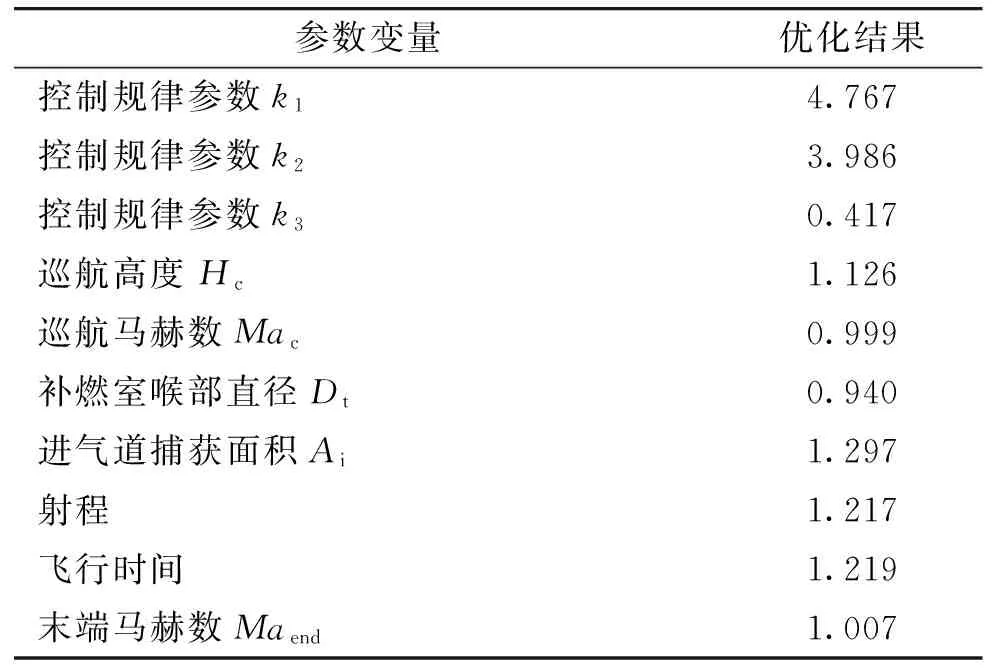
表1 优化弹道方案各参数无量纲化结果
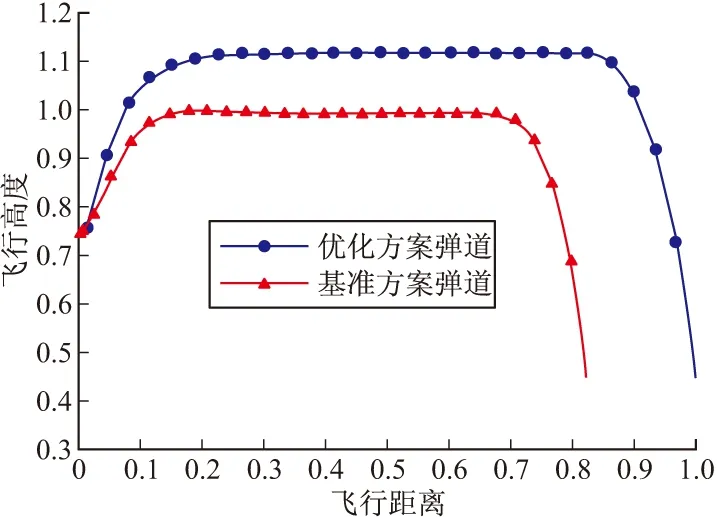
图3 铅垂平面弹道曲线
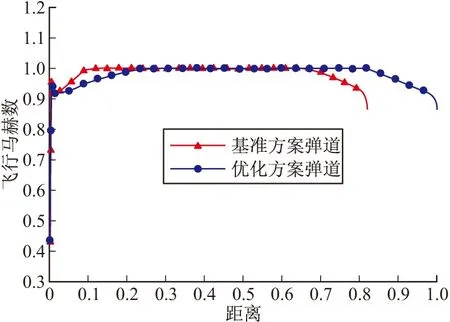
图4 马赫数变化对比曲线
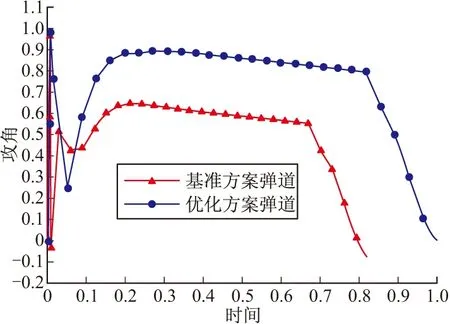
图5 攻角变化对比曲线
由以上各图可以看出,优化弹道方案相对于基准弹道方案来说,在保持巡航马赫数基本不变的情况下,巡航高度有所增加。虽然优化之后的冲压发动机推力有所下降,但由于空气密度减小使得导弹的气动阻力减小的更多,这使得导弹飞行过程中合力增大;而且固冲发动机燃气流量的减小使得固冲工作段时间延长,因此,优化后的弹道方案能够在保持末端马赫数基本一致的条件下增加了射程。同时,由于固冲发动机的设计参数(冲压喷管喉部直径,进气道捕获面积)也参与了优化,从而使得固冲发动机特性与导弹的飞行弹道特性更为匹配,满足了一体化设计的需求。
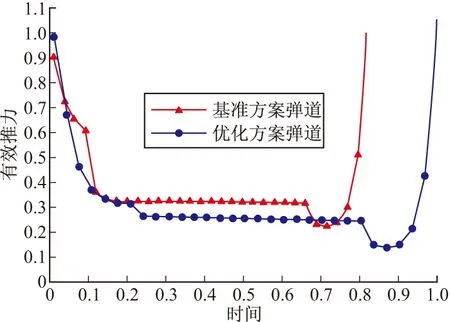
图6 冲压发动机推力变化对比曲线
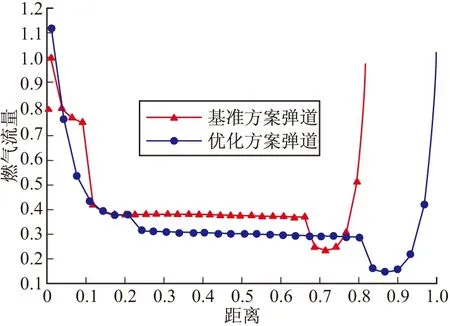
图7 冲压发动机燃气流量变化对比曲线
4 总结与展望
综上所述,可得出以下结论:
1)文中所用优化方法结合了遗传算法鲁棒性较好、全局寻优能力较强和二次序列规划法算法计算效率高、收敛性好的优点,是一种行之有效的组合优化方法。
2)以固冲发动机为动力装置的导弹其内外弹道参数相互之间具有强耦合性,在弹道方案设计中,需要对其进行综合分析。通过内外弹道一体化优化设计,可较好的兼顾固冲发动机的性能和导弹的弹道性能,提升导弹的设计潜力。
文中所做的工作是基于射程最大而进行优化的,是一个单目标优化问题。而在导弹的方案弹道实际设计过程中,需要考虑的因素很多,如为保证突防性和机动性,需要使得导弹的末速度最小;为减小对载机的影响,需要使得导弹发射质量最小等等。因此,如何在各项任务和目标中取得折衷,对固冲发动机导弹方案弹道进行多目标优化,将是未来研究的方向。
[1] 曹军伟, 王虎干. 固体火箭冲压发动机在空空导弹上应用的优势 [J]. 航空兵器, 2009(2): 47-49.
[2] 刘恒军, 沙建科, 王华. 冲压发动机导弹弹道多目标优化 [J]. 系统仿真学报, 2009, 21(9): 2764-2766.
[3] HARTFIELD Roy J, JENKINS Rhonald M, BURKHALTER John E. Ramjet powered missile design using a genetic algorithm: AIAA 2004-0451 [R]. 2004.
[4] 李新国, 方群. 有翼导弹飞行动力学 [M]. 西安: 西北工业大学出版社, 2005: 55.
[5] BAUER Christoph, DAVENNE Francois, HOPFE Norman, et al. Modeling of a throttleable ducted rocket propulsion system: AIAA 2011-5610 [R]. 2011.
[6] 鲍福廷, 黄熙君, 张振鹏, 等. 固体火箭冲压组合发动机 [M]. 北京: 中国宇航出版社, 2006: 291-293.
[7] 沙建科, 施雨阳, 万自明, 等. 冲压发动机导弹轨迹/总体参数一体化优化设计 [J]. 系统仿真学报, 2014, 43(3): 37-42.
[8] 陈宝林. 最优化理论与算法 [M]. 北京: 清华大学出版社, 1989: 314-315.
[9] 汪定伟, 王俊伟, 王洪峰, 等. 智能优化方法 [M]. 北京: 高等教育出版社, 2007: 20-24.
欢迎订阅《弹箭与制导学报》
《弹箭与制导学报》是由中国科学技术协会主管、中国兵工学会主办、中国兵器工业第203研究所承办的学术性刊物。本刊的宗旨是报道导弹、火箭、弹药、弹道及制导兵器技术相关专业的学术性论文,突出报导高新技术在本专业领域方面的理论研究成果,反映科研、生产、使用、教学上的最新应用成果,为我国国防现代化建设服务。
本刊为中文核心期刊。被美国《剑桥科学文摘:工程技术》(CSA)、美国《乌利希期刊指南》(UPD)、英国《物理学、电技术、计算机及控制信息社数据库》(INSPEC)、 日本《日本科学技术振兴机构数据库》(JST)收录。是《中国科技论文统计与分析》、《中国学术期刊文摘》、《中国科学引文数据库》、《中国学术期刊综合评价数据库》源刊;已入网“万方数据——数字化期刊群” 、“中国知网”即《中国学术期刊(光盘版)》以及《中文科技期刊数据库》(维普)。本刊国内外公开发行。
《弹箭与制导学报》为双月刊,大16开,彩色印刷,定价:每期50.00元、全年300.00元。
邮局汇款:西安市丈八东路10号学报编辑部 邮编:710065
收款人:弹箭与制导学报学报编辑部
银行汇款: 户名:西安现代控制技术研究所
开户银行:中国工商银行西安南大街支行 账号:3700 0201 0900 3706 536
联系人:何晓东 电话:02988293167 传真:02988293333
通信地址:西安市丈八东路10号学报编辑部 E-mail:djzdxb@163.com 邮编:710065
Solid Ramjet Powered Missile Project Trajectory Design and Optimization
ZHANG Leiyang,SUN Zhenhua,HE Yongjie
(China Airborne Missile Academy, Henan Luoyang 471009, China)
In view of strong coupling of thrust and trajectory characteristic of solid ramjet powered missile, a corresponding project trajectory optimization model was established, and an integrated method of genetic algorithm and sequence quadratic program was used for integrated trajectory missile optimum design which focuses on maximum range. The trajectory simulation result demonstrates that the range is improved by 21.7% while all flight condition and engine design constraints are met. The result also validates effectiveness of optimization method used by this article and necessity of integrated optimum design.
solid ramjet; project trajectory; integrated design; optimization
2015-07-12
张磊扬(1989-),男,河南洛阳人,硕士研究生,研究方向:固体火箭冲压发动机总体设计。
V435
A

