惯导/数据链组合导航技术在诱饵导弹中的应用*

温 琦,陈 凯,闫 杰

(西北工业大学航天学院,西安 710072)



惯导/数据链组合导航技术在诱饵导弹中的应用*

温 琦,陈 凯,闫 杰

(西北工业大学航天学院,西安 710072)

针对作战飞机在突入敌方防空范围时,会面临地面防空武器和空空导弹拦截的问题,提出诱饵导弹基于惯导/数据链组合导航的编队飞行模式来提高飞机生存概率。考虑该编队由领机和诱饵导弹组成,诱饵导弹通过伪距测量,利用卡尔曼滤波器,得到自身的精确相对位置。采用编队飞行轨迹发生器产生运动轨迹,通过系统仿真表明:纬度和经度误差均小于5 m(1σ),高度误差小于20 m(1σ)。仿真结果证明了该方法的有效性与可行性。

数据链;伪距;组合导航

0 引言

在现代战争中,近战格斗作战飞机容易受到地面防空武器和空空导弹的拦截,因此经常需要预先抛射诱饵导弹,组成飞行编队,模拟作战飞机的飞行轨迹,对导弹进行干扰,从而保证作战飞机的安全。

文献[1]提出了一种基于数据链无线电测距功能实现智能导弹协同定位的方法,推导了编队作战的协同定位模型;文献[2]提出利用数据链测距来跟踪高导航精度的主导航源,来改善长航时协同定位中导航精度不高的问题;文献[3]提出了一种利用H∞滤波来确定精确相对位置和相对速度的方法;文献[4-5]对JTIDS/SINS组合导航的编队飞行模式进行了全面系统的介绍,提出了编队飞行中基于四元数的无迹卡尔曼滤波融合技术,来减小相对定位解算误差。

依据以上思想,文中基于诱饵导弹编队飞行工作方式,研究了在相对网格坐标系下,惯导/数据链基于伪距测量的组合导航的方式,通过数学仿真对该组合导航系统进行仿真。

1 问题的描述

1.1 诱饵导弹编队飞行模式

文中研究的编队主要由领机(即作战飞机)和诱饵导弹组成。领机到预定区域前,可预先发射诱饵导弹,模拟作战飞机编队飞行,诱骗敌方防空武器系统攻击,消耗敌防空武器,饱和敌防空系统雷达,建立安全空中走廊,掩护领机执行作战任务[6]。系统编队飞行模型示意图如图1所示。

1.2 系统组合导航原理

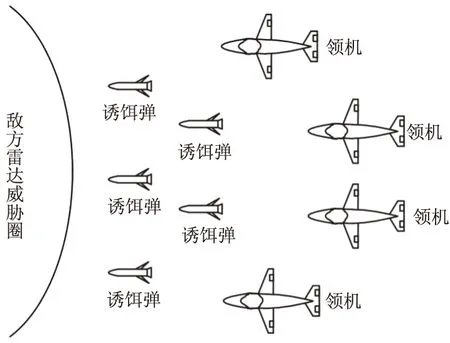
图1 系统编队飞行模型示意图

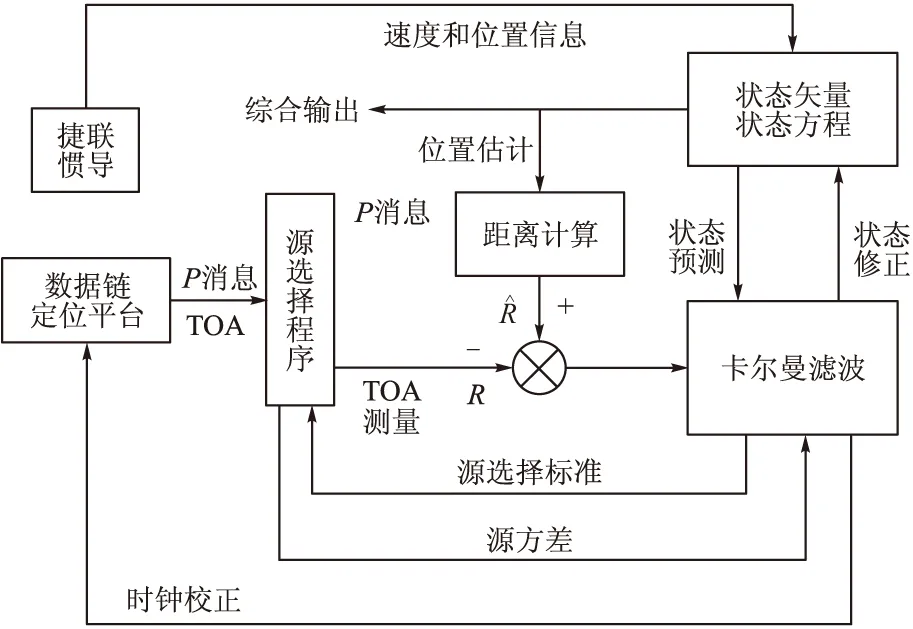
图2 系统组合导航原理图

2 相对网格坐标的计算

2.1 相对网格坐标系的定义

在相对网格坐标系中进行导航时,首先要指定一个导航控制成员(简称为导航源),将其在地球海平面高度上的投影点作为网格原点,由其来建立一个与地球表面相切的切平面网格,作为相对导航网格[8]。相对网格坐标系为直角坐标系,通常将通过该点的当地东向和北向分别作为相对网格坐标系的东向U和北向V,通过网格原点并垂直于切平面网格向上的轴作为相对网格坐标系的第三条轴W。相对网格坐标系在海平面假设静止(事实上,由于导航控制成员有航位推算误差,网格原点和V轴是在缓慢移动的。)。所有成员均在相对网格坐标系中确定自己的位置。

2.2 坐标计算

1)由经纬度坐标计算地球系坐标

(1)

式中:Re为地球卯酉圈曲率半径;e为地球第一偏心率。

2)由经纬度坐标计算相对网格坐标

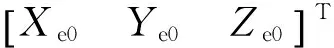
(2)

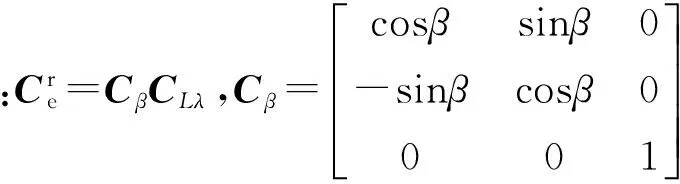
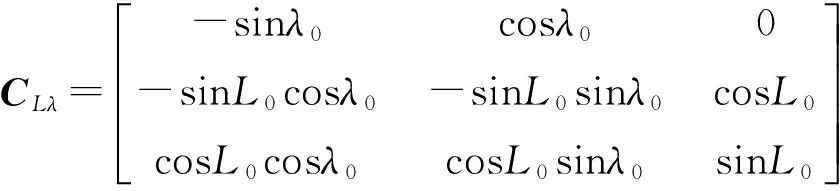
3 基于惯导/数据链的组合导航

3.1 状态方程的建立

选择相对网格坐标系为导航坐标系,系统的状态由捷联惯导参数误差、惯性元件零偏、数据链测距时钟误差和相对网格坐标系的漂移及偏转误差组成,共有22维状态。

捷联惯导参数误差和惯性元件零偏即为经典的15维捷联惯导误差方程,故不再赘述。

数据链测距时钟误差组成系统的2维状态,由与时钟误差等效的距离误差δtu和与时钟频率误差等效的距离率误差δtru组成。其误差微分方程为[1]:

(3)

式中:ωtu和ωtru分别是与时钟误差等效的距离误差和与时钟频率误差等效的距离率误差的驱动白噪声;βtru为一阶马尔可夫过程相关时间的倒数。

相对网格坐标系误差组成系统的5维状态,由网格原点沿U轴和V轴的位置漂移为δxCU、δyCV,速度漂移δvCU、δvCV和网格偏转误差β这五部分组成,其误差模型为[8]:

(4)

式中T为滤波周期。

由此,建立相对网格坐标系下惯导/数据链组合导航系统的状态方程如下:

(5)

上式中的各参数均可根据相应的误差模型得到。

3.2 量测方程的建立

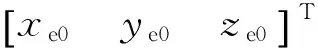
(6)

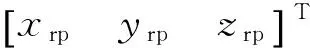
(7)

同理,在已知诱饵导弹真实位置[λLh]T时,可以得到它在相对网格坐标系下的真实坐标[xryrzr]T。

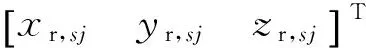
(8)

诱饵导弹上数据链接收机测得的相对于领机Sj的伪距为:

ρrL,j=rrj+δtu+νρj

(9)

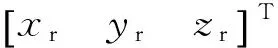
式中ej1、ej2、ej3分别为相对网格坐标系中诱饵导弹与领机之间的方向余弦值。

取4个绝对定位精度和网格定位精度都较高的领机作为导航源,则上式可具体写为:

(11)

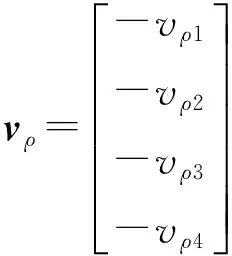
由于状态量是在地理坐标系下选取的,因此要把δxr、δyr、δzr用δL、δλ、δh表示。

将式(7)进行微分,并考虑到网格原点在W轴无位置误差,整理化简,可以得到:

(12)

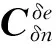
将式(12)代入式(11),可得系统量测方程为:

ZG(t)=HG(t)XG(t)+VG(t)

(13)

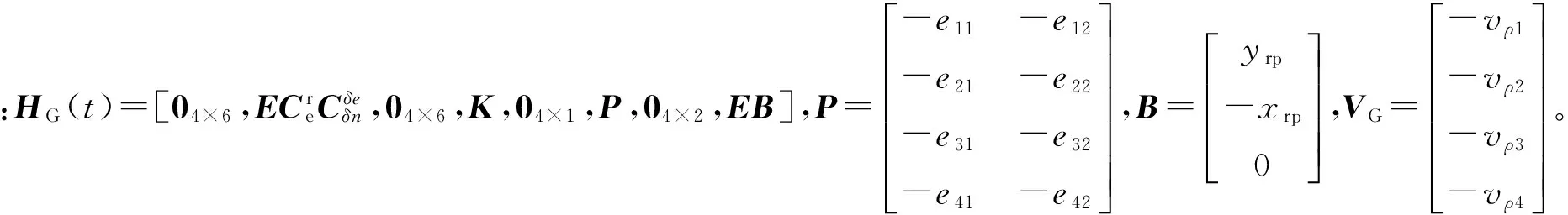
4 仿真分析

4.1 仿真条件

4架领机作为导航源,以编队的形式在空中进行飞行。诱饵导弹在领机的导引下,沿某一特定轨迹飞行。诱饵导弹的初始状态及系统误差如下:

1)诱饵导弹初始状态

航向角20°,俯仰角、横滚角均为0°;东向速度102.6m/s,北向速度281.9m/s,天向速度0m/s;纬度34.16°,经度108.95°,高度5 500m。

2)诱饵导弹初始误差

航向角误差200′,俯仰角、滚转角误差均为100′;东向速度误差0.5m/s,北向速度误差0.4m/s,天向速度误差0.6m/s;纬度误差200m,经度误差250m,高度误差300m。

3)网格坐标系误差

由原点设U轴、V轴的漂移为20 m,网格偏转误差为1°。

4)系统白噪声

陀螺仪0.5°/h(1σ),加速度计10-4g(1σ);网格原点漂移1 m(1σ),网格坐标系偏转0.1°/h(1σ)。

4.2 仿真结果

惯导/数据链组合导航姿态误差、速度误差和位置误差分别如图3～图5所示。

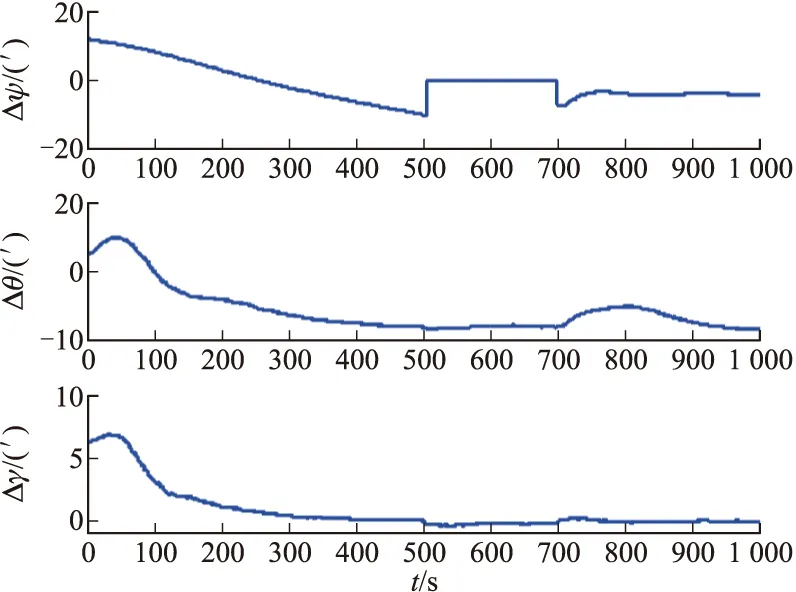
图3 惯导/数据链组合导航姿态误差

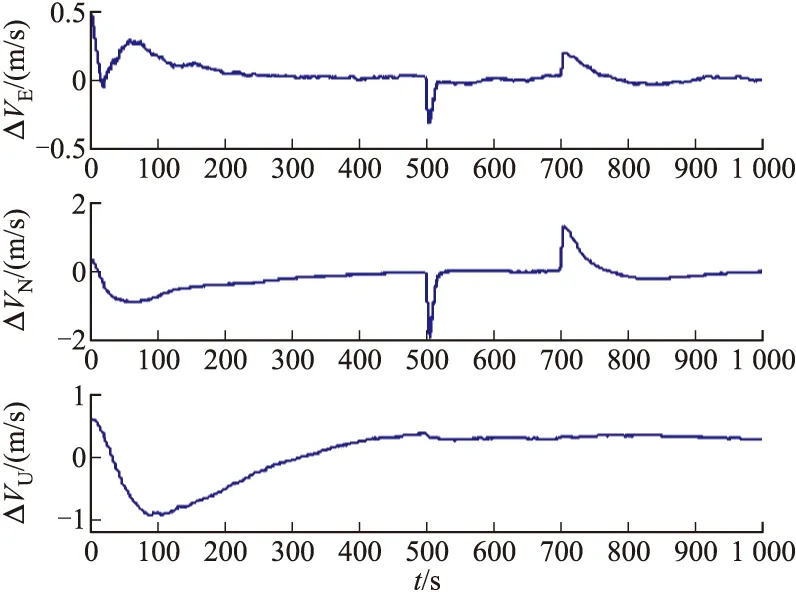
图4 惯导/数据链组合导航速度误差

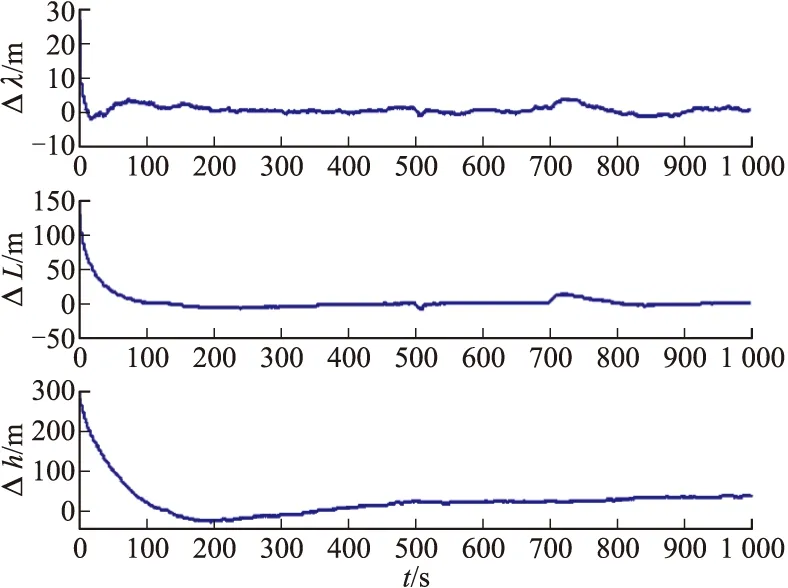
图5 惯导/数据链组合导航位置误差

从图3～图5可以看出,经过组合导航对系统状态的调整,诱饵导弹各导航参数误差均获得了显著的收敛效果:在1 000 s的仿真结束时,组合导航系统的航向角和俯仰角误差稳定在2′以内,横滚角误差稳定在1′以内;东向、北向、天向速度误差均稳定在0.3 m/s以内;纬度和经度误差稳定在5 m以内,高度误差则稳定在20 m以内。可见,组合导航系统具有较高的定姿、定位和测速精度,而且导航误差不随时间发散。

通过图4可以看出,当在500 s作快速左转弯机动,在700 s作快速右转弯机动后,诱饵导弹东向、北向速度误差仍能快速趋于收敛。而天向速度精度要低很多,这是由系统天向速度误差的可观测性较弱所引起的。

通过图5可以看出,系统的高度误差相对于纬度和经度误差要大很多,这是由于相对定位是在相对网格坐标系中进行的,而建立的相对网格坐标系是一个切平面直角坐标系,即二维坐标系,对高度方向的误差没有校正能力所导致的,在实际使用时应引入外部高度阻尼进行校正。

因此,根据上述仿真结果可以得出以下结论:惯导/数据链组合导航系统具有较高的定姿、定位和测速精度,其状态误差能很快趋于收敛。

5 结论

通过对诱饵导弹编队飞行导航原理的分析,建立了相对网格坐标系下,基于数据链伪距测量的惯导/数据链组合导航模型。将领机与诱饵导弹之间的相对位置信息与诱饵导弹的捷联惯导信息相结合,实现了诱饵导弹的精确定位。文中的相关理论对提高作战飞机生存概率具有重要的意义,也为诱饵导弹编队飞行模型及机动控制模型的建立打下了良好的基础。

[1] 王小刚, 郭继峰, 崔乃刚. 基于数据链的智能导弹协同定位方法 [J]. 中国惯性技术学报, 2009, 17(3): 319-323.

[2] CUI Tianshu, ZHANG Qingzhen, ZHANG Yaolei. A new method of cooperative localization for a long range

flightformatio [C]∥Instrumentation, Measurement, Computer, Communication and Control, 2011 First International Conference on IEEE, 2011: 933-936.

[3] WANG Yandong, YANG Shaoshuai, HU Huafeng, et al. Relative navigation algorithm based on robust filter for UAV formation flight [C]∥Proceedings of the 2012 International Conference on Control Engineering and Communication Technology. IEEE Computer Society, 2012: 249-252.

[4] WILSON D B, GOKTOGAN A H, SUKKARIEH S. A vision based relative navigation framework for formation flight [C]∥Robotics and Automation (ICRA), 2014 IEEE International Conference on IEEE, 2014: 4988-4995.

[5] WIDNALL W S, GOBBINI G F, KELLEY J F. Decentralized relative navigation and JTIDS/GPS/INS integrated navigation systems [R]. Massachusetts, America: Department of Aeronautics and Astronautics Massachusetts Institute of Technology, 1982.

[6] 杨会林, 邹敏怀, 王少锋. 空射诱饵发展分析 [J]. 教练机, 2012(1): 48-51.

[7] 林伟, 邹俊锋, 占明锋. CEC/SINS组合的相对导航与定位算法 [J]. 海军工程大学学报, 2011, 23(1): 51-57.

[8] Myron kayton, Walter R Fried. Avionics navigation systems [M]. New York: John Wiley & Sons, 1997: 288-289.

Integrated SINS/Data Link Navigation Technology Applied to Decoy Missiles

WEN Qi,CHEN Kai,YAN Jie

(School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China)

Since combat aircrafts are faced with ground-air defense weapons and air-to-air missile interception when assaulting enemy anti-aircraft range, a method using decoy missiles’ formation flight was proposed, which is based on integrated SINS/data link navigation, to increase combat aircrafts’ survival probability. Considering the formation is composed of leader fighters and decoy missiles, decoy missiles obtain pseudo range measurements from data link. Combining with Kalman filtering method, decoy missiles get its precise relative position. The trajectory is generated by the formation trajectory generator, and the results of digital simulation show that the latitude and longitude error are less than 5 m(1σ), and the height error is less than 20 m(1σ). Effectiveness and feasibility of the method have been verified.

data link; pseudo range; integrated navigation

2015-06-04

国家自然科学基金(90816027);航空科学基金(20135853037);航天技术支撑基金(2013-HT-XGD-15)资助

温琦(1992-),男,陕西洛南人,硕士研究生,研究方向:惯性导航、组合导航。

V249.3

A