关于“贝特朗悖论”的思考

石青玉

中图分类号：G634文献标志码：A文章编号：2095-9214（2016）11-0051-01

1899年，法国学者贝特朗（Joseph Bertrand）提出来一个有多种相悖解法的问题：在圆内任取一条弦，求弦的长度超过圆内接等边三角形边长的概率。百多年来，争论不断，主要的有如下三种解法：

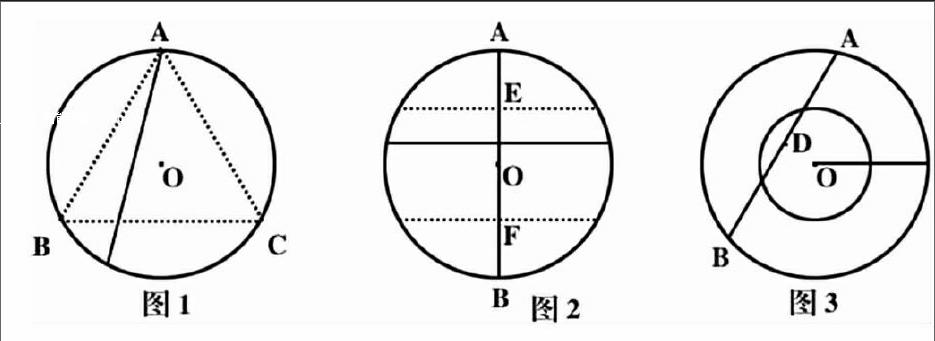
解法一：由于对称性，在圆周上任取一点A，以此为端点做一等边三角形ΔABC，从A点发出的无数条弦，显然只有那些落在ΔABC内的弦才满足条件，其对应的弧长BC为整个圆周的1/3，则所求概率为1/3（见图1）。

解法二：由于对称性，可预先指定弦的方向。作垂直于此方向的直径AB，只有交直径于1/4（E点）与3/4（F点）间的弦，其长才大于内接正三角形边长。EF等于AB的一半，故所求概率为1/2（见图2）。

解法三：以圆半径的一半为半径做一小圆，当弦的中点D在小圆内时，弦长大于，此时所求概率为小圆面积与大圆面积之比即1/4（见图3）。

同一个问题，有三种解法，通行的意见认为这三种解法是由于取弦时采用不同的等可能性假定造成的，第一种解法假定弦的端点在圆周上均匀分布，第二种解法假定弦的中点在直径上均匀分布，第三种解法假定弦的中点在圆内均匀分布。这三种假定构成了三种不同的随机试验，所以，对于各自的随机事件而言，三种解法都是正确的。还有其他的一些意见，各自支持三种解法的一种。

但是，通过使用遍历法取弦，笔者产生了不同的看法，在此提出，希望能起到抛砖引玉的作用。

考虑原题，“在圆内任取一条弦”，如何任取才能让每条弦都等可能的被取到呢？换个角度想，这种等可能取弦法一定能够遍历圆内所有的弦同样的次数。

我们先看解法一的取弦法，在圆周上任取一点A作为弦的端点，另一端点从A点开始（不含A点）逆时针旋转遍历圆周一圈，然后A点逆时针移动一点，B点再移动一圈，如此重复，等A点也移动一圈时，圆内所有弦都遍历到了2次（由于对称性），可见，解法一的取弦法是等可能性的取弦法。

再看解法二的取弦法，任取一条直径，从直径一端到另一端，遍历做垂直于此直径的弦，然后，直径逆时针移动一点，再遍历此直径做垂直的弦，等直径移动一圈，圆内所有弦也都遍历2次（由于对称性），所有，解法二的取弦法也算是等可能性的取弦法。

最后看看解法三的取弦法，在圆内任取一点D，做过此点的弦，然后再移动D点，遍历圆内所有点，重复做过此点的弦，就会发现，当D点不是圆心时，过D点的弦只有一条，而当D点遍历到圆心时，过该点的弦有无数条，因此，解法三的取弦法不能算作等可能性的取弦法，解法三应该从正确的解法中去除。

我们再来看看解法一和解法二，想象一下，两个人分别用解法一和解法二的取弦法遍历同一个圆，分别构造了圆内所有弦的两个样本空间，不妨命之为空间一和空间二。不难想象，对于空间一的每一条弦，都有空间二的一条弦相对应，而对于空间二的每一条弦，也都有空间一的一条弦相对应，也就是说，空间一和空间二的元素一一对应，即两个样本空间是等价的。

综上所述，笔者认为，解法一和解法二都是符合题意中等可能性的，也是等价的，都是正确的，而解法三是错误的。至于为什么样本空间等价的解法一和解法二会有不同的概率值，笔者大胆的提出一个猜测：对于具有无穷事件组成的样本空间而言，概率值不是固有的属性，是和取样法高度相关的。不知对否，还希望各位专家提出宝贵意见。

（作者单位：山东省实验中学）

参考文献：

[1]黄晶晶，黄世同.关于贝特朗悖论的新思考.昆明师范高等专科学校校报，2004，26（4）：10-12.

[2]苏同安.都是圆心惹的祸——“贝特朗悖论”新说.山东省桓台第一中学.中学数学，2010（1）：64.

[3]黄加流.也谈“贝特朗悖论”——驳“都是圆心惹的祸”.广东省珠海市第一中学.中学数学，2011（11）：61-62.

[4]张敏，何小亚.贝特朗悖论之争的终结.华南师范大学数学科学学院.数学教育学报，2015，24（3）：51-54.

[5]石启亮.解读贝特朗悖论.山东省郯城县美澳学校.数学教学，2015（10）：32-34.