立体几何中的探索性与存在性问题例说

山东省枣庄二中 韩宏帅

立体几何中的探索性与存在性问题例说

山东省枣庄二中 韩宏帅

探究性与存在性问题是指一类在条件不完备的情况下探讨某些结论能否成立的问题。立体几何中的探究性与存在性问题，既能够考查同学们的空间想象能力，又可以考查同学们的观察、分析和探究能力。

热点题型

1.对命题条件的探索

探索条件，即探索能使结论成立的条件是什么。对命题条件的探索常采用以下三种方法：（1）先猜后证，即先观察与尝试给出条件，再进行证明。

（2）先通过命题成立的必要条件探索出命题成立的条件，再证明充分性。

（3）把几何问题转化为代数问题，探索出命题成立的条件。

2.对命题结论的探索

探索结论，一种是在给定的条件下命题的结论是什么，常从条件出发，探索出要求的结论是什么；还有一种是探索结论是否存在，常假设结论存在，再寻找与条件相容还是矛盾的结论。

解题技巧

立体几何的探索性与存在性问题一般都是条件开放性的探究问题，采用的方法一般是执果索因的方法：假设求解的结果存在，寻找使这个结论成立的充分条件，运用方程的思想或向量的方法转化为代数的问题解决，如果能找到符合题目结果要求的条件，则存在；如果找不到符合题目结果要求的条件，或出现了矛盾，则不存在。

典例选析

例1 如图1，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，P A⊥PD，PA=PD，AB⊥AD，AB=1，AD=2，AC=CD=。

图1

（1）求证：PD⊥平面PAB。

（2）求直线PB与平面PCD所成角的正弦值。

（3）在棱PA上是否存在点M，使得BM∥平面PCD？若存在，求的值；若不存在，说明理由。

分析 （1）由面面垂直性质定理可知AB⊥平面PAD，根据线面垂直性质定理可知AB⊥PD，再由线面垂直判定定理可知PD⊥平面PAB。

（2）取AD的中点O，连接PO、CO，以O为坐标原点建立空间直角坐标系O-xyz，利用向量法可求出直线PB与平面PCD所成角的正弦值。

图2

点评 平面与平面垂直的性质的应用：当两个平面垂直时，常在其中一个面内作交线的垂线，把面面垂直转化为线面垂直，进而可以证明线线垂直（必要时可以运用平面几何的知识证明垂直关系），构造（寻找）二面角的平面角或得到点到面的距离等。

例2 如图3，在梯形ABCD中，AB∥CD，AD=DC=CB=a，∠ABC=60°，四边形ACFE是矩形，且平面ACFE⊥平面ABCD，点M在线段EF上。

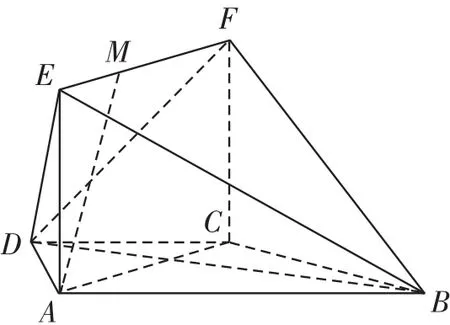
图3

（1）求证：BC⊥平面ACFE。

（2）当EM为何值时，AM∥平面BDF？证明你的结论。

分析 （1）证明线面垂直的方法：一是利用线面垂直的判定定理，二利用是面面垂直的性质，三是利用平行线法（若两条平行线中的一条垂直于这个平面，则另一条也垂直于这个平面）。解题时，注意线线、线面与面面关系的相互转化。

（2）证明线面平行常用方法：一是利用线面平行的判定定理，二是利用面面平行的性质。

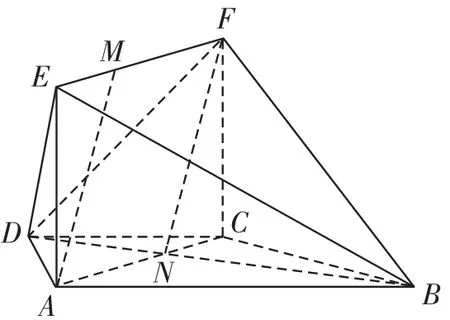
图4

点评 本题考查了直线与平面垂直的判定和直线与平面平行的判定。这类探索性题型通常是找命题成立的一个充分条件，所以解这类题采用下列两种方法：（1）通过各种尝试探索出条件。（2）找出命题成立的必要条件，再证明充分性。