城市轨道交通列车运行能耗优化研究
赵 迪 刘 格 杨贝贝
(湖北工业大学机械工程学院,430068,武汉∥第一作者,讲师)
城市轨道交通列车运行能耗优化研究
赵 迪 刘 格 杨贝贝
(湖北工业大学机械工程学院,430068,武汉∥第一作者,讲师)
研究了单列和多列列车运行能耗优化决策问题。城市轨道交通系统对能源的需求量非常大,通过对列车的合理调度,可使列车的运行能耗进一步降低。列车运行环境和线路路型的复杂性,导致列车运行过程中其本身所受到的力是随时变化的。通过模拟现实列车运行状态得出优化模型,具有十分重要的理论意义和应用价值。主要采用极大值原理、非线性方程模型、多目标二次规划对列车消耗的能量进行优化。在能量最优化的情况下,对速度与位移和时间与速度的变换规律进行了研究。
城市轨道交通; 列车; 能耗; 节能
Author′s address School of Mechanical Engineering, Hubei University of Technology,430068,Wuhan,China
低碳环保、节能减排日益受到关注,在城市轨道交通领域,减少列车牵引能耗的列车运行优化控制近年来已成为重要的研究方向。城市轨道交通系统的能耗是指列车牵引、通风空调、电梯、照明、给排水、弱电等设备产生的能耗。根据统计数据,列车牵引能耗占城市轨道交通系统总能耗的40%以上。本文主要通过优化城市轨道交通列车运行的速度距离曲线和多列车运行的停站间隔时间,以达到运行能耗最低的目标。
目前,国内外针对城市轨道交通列车节能的研究较多。有学者通过列车节能优化操纵算法研究,提出列车运行中如果能够按限速运行时就尽量减少制动;有学者同样认为,节能性列车操控应该是避免损失列车的动能,少用制动操作,在上下坡过程中可合理利用车辆的势能,将其转化为列车必须的动能,同时减少由于基本阻力所造成的能量损失。
1 问题描述
列车在站间运行时会根据线路条件、自身列车特性、前方线路状况等计算出一个限制速度,限制速度会周期性更新,列车运行速度不允许超过此限制速度。在此约束下,列车运行工况通常包括牵引、巡航、惰行和制动4个阶段,每个阶段所受到的牵引力和阻力都不相同。
对于单列车节能运行优化控制,主要是寻找一条速度距离曲线,使得列车在相邻两站间的规定总运行时间内能耗最低。对于多列车多站运行节能优化控则要考虑停站时间、制动能量回收与利用等影响因素。
2 列车运行过程分析
图1为列车站间运行曲线。
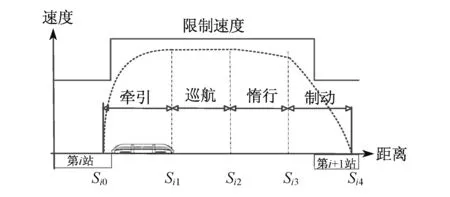
图1 列车站间运行曲线
根据图1所示,对每个工况阶段的分析如下:①牵引阶段,列车加速运行,电机耗能;②巡航阶段,列车匀速运行,是否需要牵引取决于当时受到的总阻力;③惰行阶段,列车既不牵引也不制动,列车运行状态取决于总阻力,电机不耗能;④制动阶段,列车减速运行,电机不耗能(电阻制动方式除外)。如果列车采用再生制动技术,此时可以将动能转换为电能反馈回供电系统供其他用电设备使用。
如果当车站间距离较短时,列车一般采用“牵引—惰行—制动”的策略运行。如果站间距离较长,列车通常会采用牵引到接近限制速度后,交替使用惰行、巡航、牵引3种工况,直至接近下一车站采用制动进站停车。
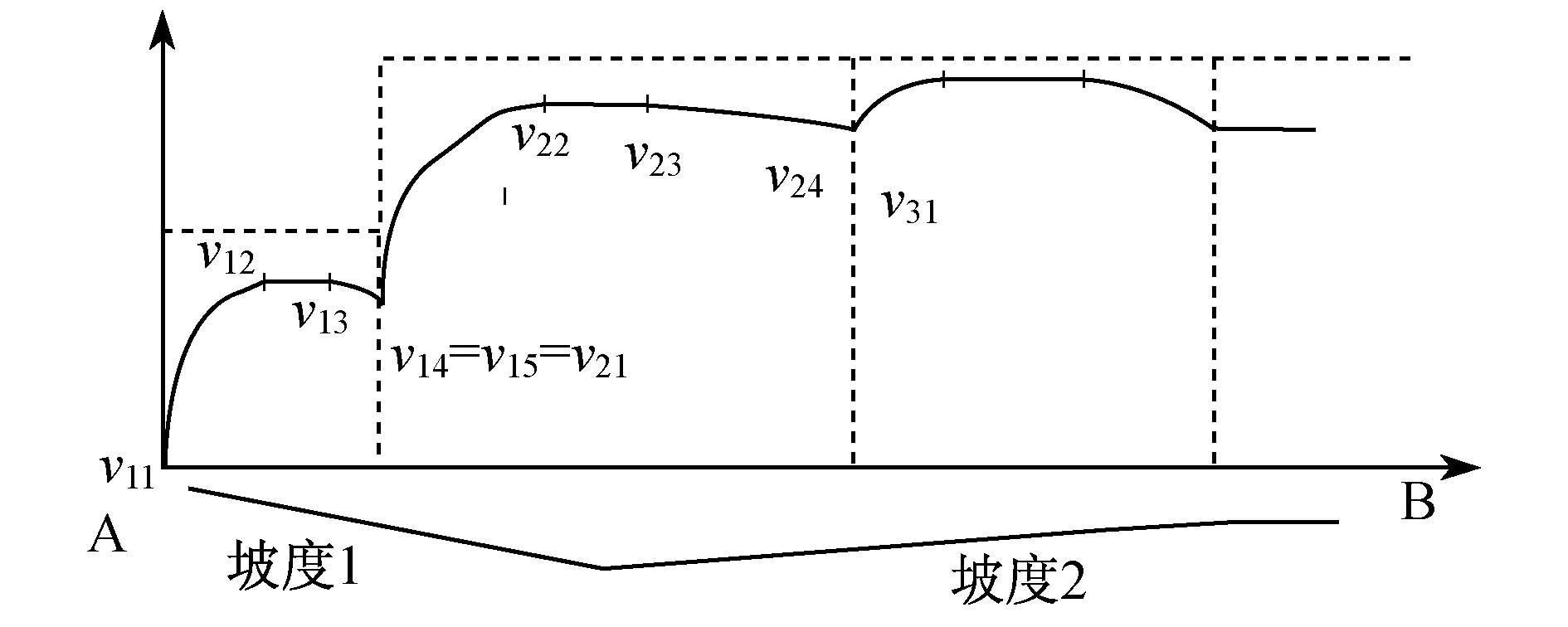
节能驾驶运行状态序列由6种最优控制模式和5种轨迹结合按顺序组成[1]。按照所有运行工况也可以分为6个阶段,即:最大牵引变速—匀速(最大牵引或部分牵引)—变速(惰行)—匀速(惰行或部分制动)—减速(制动)—加速(最大牵引)[2]。
3 列车物理特性分析
列车在运行过程中,实际受力状态非常复杂。本文采用单质点模型,将列车视为单质点,列车运动符合牛顿运动学定律。其受力可分为4大类:重力G、牵引力F、制动力B和总阻力W。
列车牵引力在不同加速度下存在不同的最大值。根据受力平衡分两种情况:
当列车处于下坡(包括平路)轨道时:
B+W=μFmax+G×sinθ
(1)
式中:
μ——实际牵引加速度与最大加速的比。
Fmax——列车最大牵引力。
当列车处于上坡轨道时:
B+W+G×sinθ=μFmax
(2)
假设一:在列车减速阶段,电机不耗能量,车辆采用常用制动方式[8](为了简化模型并未考虑制动电阻的能耗)。
假设二:由于列车实际受力状态非常复杂,可以把列车当做质点来研究。
假设三:列车运行中除运动部件所受的总阻力之外不受其他的阻力。
假设四:列车运行中可以严格按照要求进行制动和牵引操作,不存在人为因素。
假设五:所有列车处于同一供电区段,其他条件都是一样的。
当列车在站间运行时,存在着多条速度距离曲线供选择。不同速度距离曲线对应不同的站间运行时间和不同的能耗。一般认为,列车站间运行时间和能耗存在近似的反比关系。
4 单列车运行能耗优化
列车在不同线路条件(水平、下坡和上坡)受到的阻力是关于速度的二次函数曲线。分析可知,单列车的运动方程可以用式表达:
(3)
(4)
式中:
uf,ub——分别为牵引力和制动力系数;
v——列车运行速度;
Bmax——列车最大制动力;
v(x),t(x)——分别为列车速度在路程x处的速度和位移。
由此可以得到能耗模型为:
(5)
式中:
J——列车能耗;
据此可以得到以下四种可能的优化控制模式:
(1) 用最大牵引力加速运行,即uf=1,ub=0;
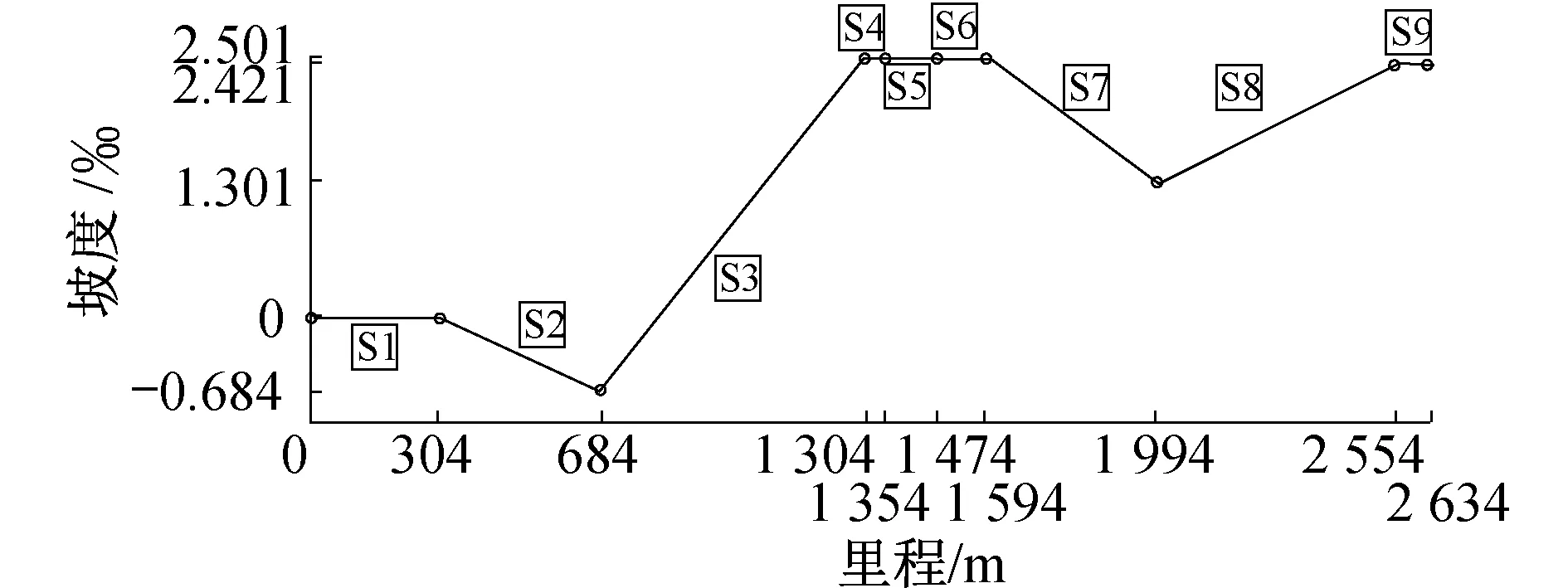
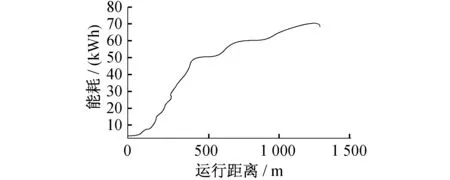
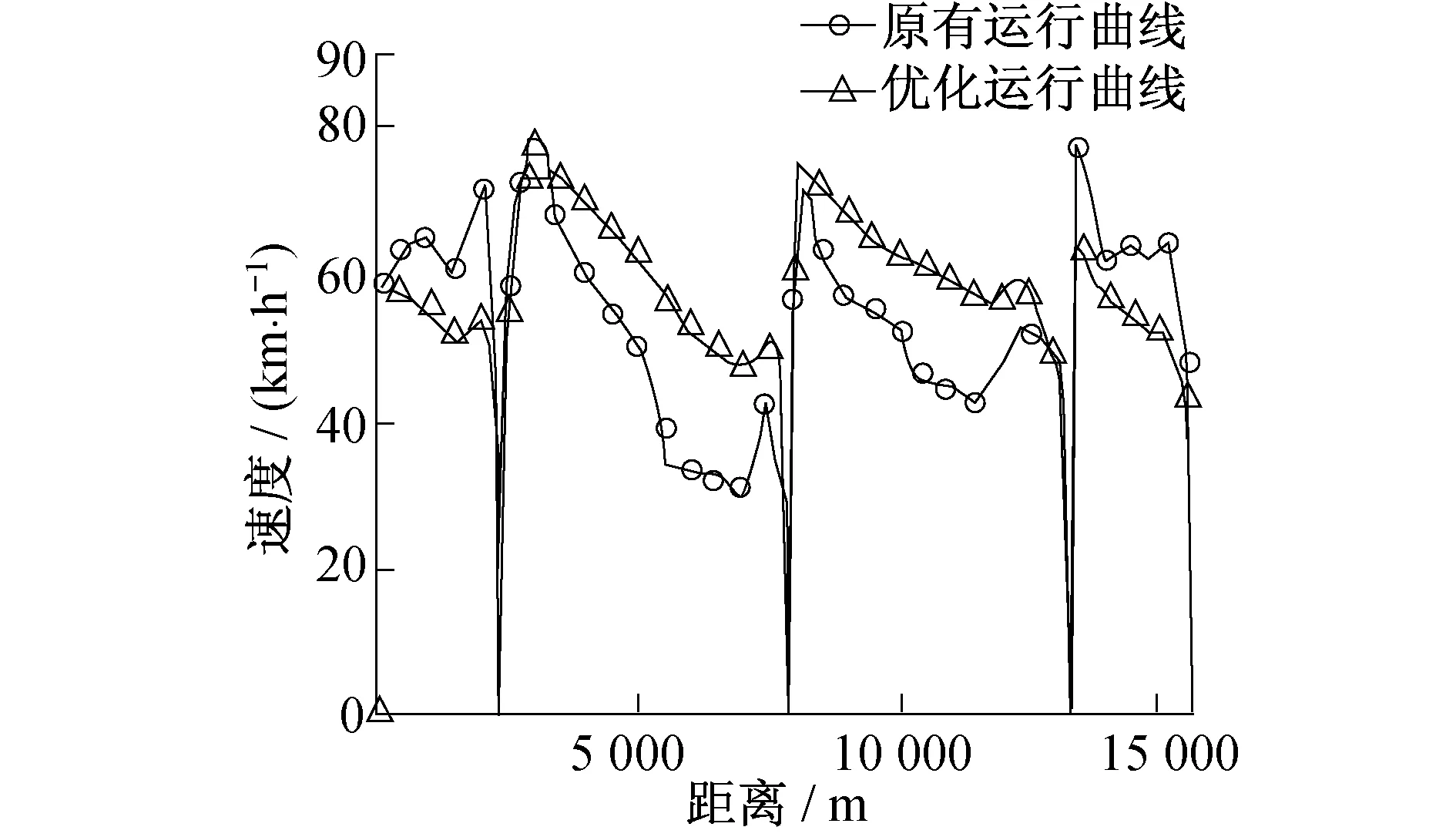
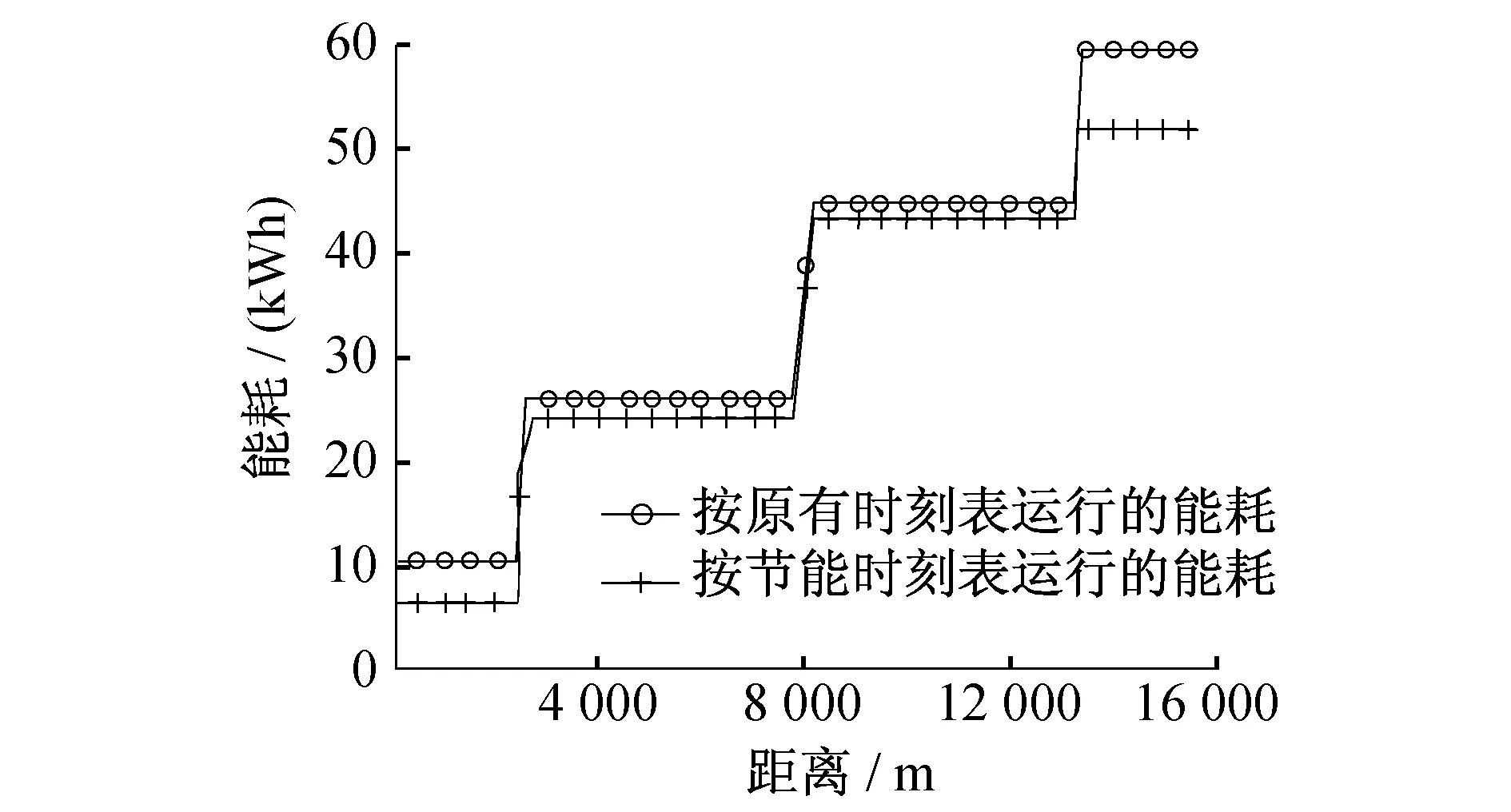
(2) 使用部分牵引力或部分制动力维持匀速运行,即0 (3) 既不牵引也不制动,列车处于巡航状态,即uf=ub=0; (4) 用最大制动力制动,即uf=0,ub=1。 由以上分析可知,在某种路型段消耗的总能量可表示为: (6) 式中: a——减速度; g(x)——坡道阻力; w0——运行租力; h——坡道的运行时间; r——其他阻力; S——列车平均运行时间; T——列车平均时间; 上述目标函数的求解可看成非线性目标规划问题,而其约束条件是运行时间、路程和限制速度。本文选择速度vi作为决策变量,使用优化控制方法可得如图所示的最低能耗速度与距离曲线。 图2 最低能耗时的速度与距离曲线 城市轨道交通常见坡道纵断面形式有V型坡(坡度3‰~26‰)、单面坡和W型坡(坡度2‰~25‰)[14]。某城市轨道交通线路两站之间坡度与距离实际路况如图3所示。图4为拟合模型的列车消耗能量与距离关系图(以W坡为例)。 图3 某城市轨道交通线路两站(A6到A8)的实际路况图 图4 拟合模型的列车消耗能量与运行距离关系图 多数情况下两站点之间并不是单一路型,实际上可能会有多个坡度。因此,根据上文所建模型,按限速将站点间距离分割为N个部分,用i标记,i∈[1,N],每一段运行时间和运行距离分别为ΔTi,ΔSi,每一段的限速为vi,lim。由单一路段建立的模型可知,优化控制序列在不同部分是不同的。在速度限制不变的部分,列车不需要制动。将每一部分分成4个控制阶段,如图5所示,在每个部分中,vi1和vi2之间是加速阶段,vi2和vi3之间是匀速阶段,vi3和vi4之间是巡航阶段,vi4和vi5之间是匀速阶段。但由于第一部分和第二部分为一般坡度,故vi4=vi5。在每个部分中,用j作为表示控制阶段,j=1,2,3,4。i部分j阶段的速度为vij,并且易知vi5=v(i+1)1。 图5 速度与制动力的特征曲线 根据单一路况模型和能量守恒原理易知,在i部分单位质量能耗为: g·Δhi+ΔEi,w0 (7) 每部分运行时间和运行距离可参照上述模型计算,故可以得到优化模型: (8) 该模型是一个同时含有等式约束和不等式约束的非线性规划问题。可采用序列二次规划方法(SQP)求解。记约束总数为m,其中有n个等式约束、m-n个不等式约束。约束个数取决于子区间个数和坡度。将模型改写为下式: (9) 本文所采用的SQP算法使用以上拉格朗日函数的二次近似来求解前文提到的二次规划(QP)子问题,此时的约束是线性的。之后再把线性关系转化成非线性约束条件得到问题的解,因而求解的结果是近似解。 由于整条线路均采用一条供电线路,即产生再生能源可用于行驶在线路上正处于牵引状态的各列车共享。因此能量再生模式可归为单供电系统模式。 再生制动能量利用的核心是:通过调度,使列车制动能量在同一时刻能够被同一供电区段内有需求的牵引列车使用。这时列车的牵引时间、惰行时间、巡航时间和制动时间都是系统的调节变量。优化这些变量,能够提高再生制动能量的使用效率。针对城市轨道交通系统,本文所建立模型不考虑两车间距超过一个站间的情况。 设n车出i+1站加速,n+1车进i+1站减速,如果n+1车和n车的供电区段重叠,n车可以使用n+1车的再生制动能量进行牵引;n车进i+1站减速,n+1车出i站加速,如果n+1车和n车的供电区段重叠,n+1车可以利用n车的再生制动能量牵引。 基于节能的列车调度表,其优化目标是整条线路总能耗最低,理想状态是列车再生制动能源全部被回收用于列车牵引。调度、再生制动能量和牵引能耗的关系为: W(H,H9,2H4-H2,H2-H4,H1-H2,H8)= H1-H2,H8) (11) 式中: Hi——第i列列车的发车时隔; Wbi——回收动能。 根据列车的牵引功率,列车牵引能耗为: (12) 式中: P——制动功率。 由上述分析可知,可将节能时刻表制定问题规划为如下模型: Wmin(H,H9,2H4-H2, H2-H4,H1-H2,H8) (13) 模型约束条件如下: Dmin≤H≤Dmax 式中: D——列车发车间隔。 在仿真软件Matlab中建立仿真模型,仿真结果如图6、图7所示。 图6 距离与速度的特征曲线 图7 距离与能量消耗特征曲线 从仿真结果中能看出,考虑制动能量回收利用,节能优化后的列车最高运行速度并没有显著降低,平均速度在全线无明显变化,列车运行效率未受到明显影响。而能量消耗在全线都有所降低,在0~2.0 km阶段和1.3~1.6 km阶段下降最为明显,起到了良好的节能效果。 该仿真模型按照同一客流量进行设计,未考虑不同时间段的客流量。实际运行过程中客流量是变化的,停站时间还可以进一步优化。若将每天按时段划分并分析,能够得到更详细的列车运行调度方案,但仿真模型将会更加复杂。通过调度列车运行间隔能够优化再生制动能量的使用效率,从而达到整条线路能耗最优。 本文以列车牵引力学为依据,从调度操控方面着重分析了城市轨道交通列车的运行节能问题。研究了列车节能控制方法,充分利用进出站坡道高差建立了列车节能控制的仿真计算模型,在已知线路条件下求解并优化了列车运行时刻。通过在仿真软件Matlab中进行仿真分析,用较小的系统开销得出了一个较为满意的列车运行方案。 仿真结果表明,采用本文所建立的能耗模型作为优化目标,对单一子区段用序列二次规划方法进行快速求解,可以使列车能耗减少。当两车在站间追踪运行时,综合两车运行信息,将两车追踪节能驾驶场景归类为节能优化问题,并建立非线性规划模型。最后釆用序列二次规划方法进行快速求解。仿真结果表明,采用本文提出的方法可以节能21%。 本文的研究过程做了部分简化和近似,算法并未考虑多种制动方式带来的能耗波动,为适应实际调度操作尚有待进一步研究。 [1] KHMELNITSKY E.On an optimal control problem of train operation[J].IEEE Transactions on Automatic Control,2000,45(7):1257. [2] LIU R F,LAKOV M.Golovitcher.Energy-efficient operation of rail vehicles[J].Transportation Research Part A:Policy and Practice,2003,37(10):917. [3] HOWLLET P.An Optimal Strategy for the Control of A Train[J].Journal of the Australian Mathematical Society.Series B.Applied Mathematics,1990,31(4):454. [4] SU S,TANG T,LI X,et al.Optimization of Multi-train operations in a subway system[J].IEEE Transactions on Intelligent Transportation Systems,2014,15(2):673. [5] MIYATAKE M,KO H.Optimization of Train Speed Profile for Minimum Energy Consumption [J].IEEE Transactions on Electric Engineering,2010,5(3):263. [6] MASAFUMI M,KUNIHIKO M.Energy Saving Speed and Charge/Discharge Control of a Railway Vehicle with On-board Energy Storage by Means of an Optimization Model [J].IEEE Transactions on Electrical and Electronic Engineering,2009,4(6):771. [7] 程国忠.轨道车节能运行方法的研究[J].管理学家(学术版),2014(12):42. [8] 夏竟成.新加坡地铁车辆牵引与制动控制系统的结构和控制技术[J].沿海企业与科技,2013(3):21. [9] 刘炜,李群湛,郭蕾,等.基于多种群遗传算法的城轨列车节能运行优化研究[J].系统仿真学报,2010,22(4):921. [10] 胡晓丹,张杰.城市轨道交通节能坡寻优研究[J].铁道工程学报,2013(5):27. [11] 中华人民共和国铁道部.列车牵引计算规程[M].北京:中国铁道出版社,1990. [12] 朱金陵,李会超,王青元,等.列车节能控制的优化分析[J].中国铁道科学,2008,29(2):104. [13] 陈必壮,王忠强,王祥.上海市轨道交通网络化客流特征分析及启示[J].城市交通,013(6):28. [14] 马小毅,金安,刘明敏,等.广州市轨道交通客流特征分析[J].城市交通,2013(6):35. [15] 陈富安.地铁节能坡设计研究[J].铁道工程学报,2013(8):104. [16] 宋云.城市轨道交通ATO模式下列车节能运行研究[J].铁路通信信号工程技术,2014,11(2):41. Optimization of Energy Consumption in Metro Train OperationZHAO Di, LIU Ge, YANG Beibei Energy consumption of metro in operation is studied, including both the single train and the multiple trains. Since the energy consumption of urban rail transit is very large, reasonable scheduling of trains will effectively reduce the energy consumption, because the stress on the train changes due to the operation conditions and the line complexities. By simulating the operation of metro train, an optimum model is established, which has important theoretical and practical values. Maximum principle, nonlinear equation model and multi-objective quadratic programming are used to optimize the energy consumption. Finally, in the optimization condition, the changing laws of subway train speed and movement, speed and time are studied. urban rail transit; train; energy consumption; energy conservation U 284.48; TK 018 10.16037/j.1007-869x.2016.05.008 2016-01-12)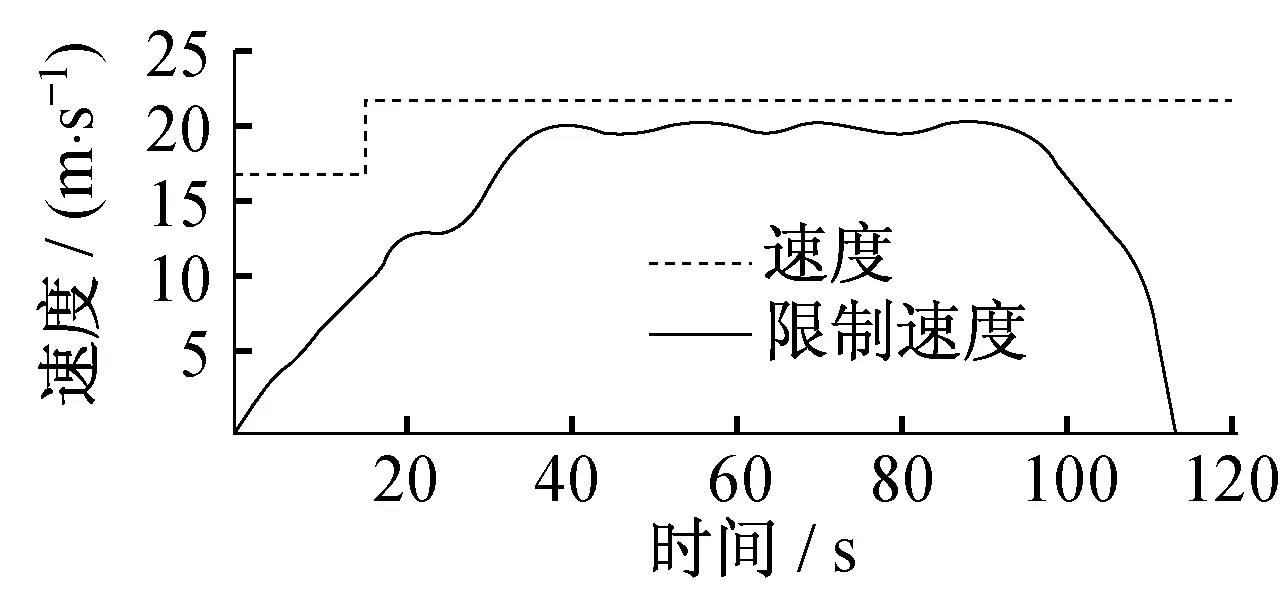
5 多列车运行能耗优化
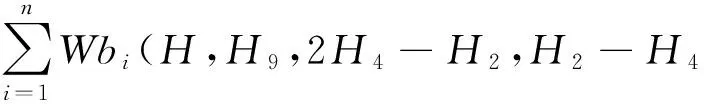
6 仿真分析结果
7 结论分析

