Jordan标准形理论解析方法的难点分解

鲍炎红

(安徽大学数学科学学院，合肥230601)



Jordan标准形理论解析方法的难点分解

鲍炎红

(安徽大学数学科学学院，合肥230601)

Jordan标准形理论是线性代数中的核心内容之一. 运用解析方法证明Jordan标准形的存在性也是线性代数的教学难点. 结合教学实践，通过分析其数学思想和数学方法，对Jordan标准形的解析方法进行难点分解.

Jordan标准形； 不变子空间； 根子空间； 循环子空间

1 引 言

相似标准形理论是线性代数中最精彩也是最深刻的部分，同时也是整个线性代数中最难掌握的部分. 一般精彩的数学理论往往都是自然的数学思想与精妙的数学方法技巧的结合. 无论是培养数学思维还是具体知识记忆，学生能体会这一数学思想的自然性更为重要. 一旦体会到这种自然性，首先就有了整体上的把握，思路也就变得清晰；其次在具体实现过程中，都会感觉到每一步也都充满着某种“必然性”.

diag(J(λ1,m1),J(λ2,m2),…,J(λs,ms))，

其中J(λi,mi) (i=1,2,…,s)为mi阶Jordan块矩阵

传统教材上Jordan标准形理论证明的方法多数采用λ-矩阵[1, 2]和解析方法[2, 3]. 在后续教学研究过程中，也不断有一些新方法出现[4, 5, 6]. 但在实际教学过程中，大多数高校都只讲授λ-矩阵的方法，即寻找矩阵相似关系的全系不变量， 并利用这些全系不变量直接构造Jordan标准形. 该方法易于直接计算线性变换的Jordan标准形，但绕开了对应的基与过渡矩阵. 因此对应的过渡矩阵需要另行计算[7, 8]，而且不容易理解Jordan标准形矩阵对应基的几何意义. 而解析法是从空间分解入手，通过寻找合适的基，使得线性变换在该组基下的矩阵恰为Jordan标准形. 这一方法的难点主要在于需要引入很多的抽象概念，如根子空间、循环子空间等. 一般初学者都难以理解为什么要这样做，每一步又是怎样做的. 在实践教学过程中，我们从介绍不变子空间开始，就以Jordan标准形为“终极目标”，逐步介绍这些概念如何运用到Jordan标准形理论中，从而起到目标明确，难点分解的效果.

本文只介绍Jordan标准形理论解析方法的基本思想与基本方法，相关结论的证明详见教材[1, 2, 3]，在此不再赘述.

2 不变子空间与空间分解

设A为复线性空间V上的一个线性变换. 往往整个空间V上的线性变换比较复杂，难以把握. 一个自然的想法就是“化整为零”，即考虑V的子空间. 设W为V的子空间，我们自然希望A能直接给出子空间W上的线性变换，即A将W中的向量仍送到W中，即对任意α∈W，都有A(α)∈W. 这就引入了不变子空间的概念. 将A自然诱导的W上线性变换记为A|W，称为A在其不变子空间W上的限制，即对任意α∈W,A|W(α)=A(α).

若能将V分解成若干个A的不变子空间的直和， 即存在A的不变子空间W1,W2,…,Ws，使得

V=W1⊕W2⊕…⊕Ws.

再对于每一个i, 选取Wi的一组基αi1,αi2,…,αiri,设A|Wi在该基下的矩阵为Ai，则α11,…,α1ri,…,αs1,…,αsrs构成V的一组基，且A在该基下的矩阵为

diag(A1,A2,…,As).

此时，也可将线性变换A写成

A=A|W1⊕A|W2⊕…⊕A|Ws.

相似标准形理论解析方法的基本思想是“化整为零，各个击破”. 具体来说，是分成两步来完成：

第一步，将V分解成若干个A的不变子空间的直和，

V=W1⊕W2⊕…⊕Ws.

使得A在每个不变子空间上的限制A|Wi都具有非常好的性质.

第二步，对于每个A的不变子空间Wi，选取合适的基，使得A|Wi在该基下的矩阵具有最好的形式.

剩下的就是数学方法与技巧的事情了. 事实上，这里也充满着很多“必然性”. 在本节，我们还需要介绍构造A的不变子空间的两种重要方法.

(i) 由向量组生成的不变子空间. 设S⊂V，则V中包含S的最小的A的不变子空间，称为由S生成的A的不变子空间. 特别地，设C(α)为由一个向量α生成的不变子空间，称为循环子空间，即

C(α)=L(α,A(α),…,Ak(α),…).

此处，我们应注意到V是有限维线性空间，因此，存在充分大的k，使得

C(α)=L(α,A(α),…,Ak(α)).

详见教材[3]定义7.3.1.

(ii) 可交换的两个线性变换相互给出不变子空间. 设A,B为V上线性变换，且AB=BA，则KerB,ImB均为A的不变子空间. 特别地，任取多项式f(x)∈[x]，f(A)与都是可交换的，因此Kerf(A),Imf(A)都是A的不变子空间.

3 可对角化的线性变换

设A为n维线性空间V上的线性变换. 按照空间分解理论，最理想的情况，也是分解最彻底的情况，就是整个线性空间A可以分解成n个1维不变子空间的直和，即

V=W1⊕W2⊕…⊕Wn,

其中Wi=L(αi)为A的1维不变子空间. 据此，我们可引入特征值与特征向量的概念. 上述最理想情况的等价描述为A有n个线性无关的特征向量α1,α2,…,αn.此时,A在基α1,α2,…,αn下的矩阵为

diag(λ1,λ2,…,λn),

其中αi为A的属于特征值λi的特征向量，i=1,2，…,n，称A为可对角化线性变换.

在教学过程中，分析线性变换可对角化的各种条件也是教学重点之一.

4 幂零变换

除可对角化的线性变换外，幂零变换也是一类非常重要的线性变换. 今后我们会看到，任一个线性变换都可以写成一个可对角化线性变换与一个幂零变换之和，分别称为该线性变换的半单部分和幂零部分.

所谓幂零变换，是指存在正整数m，使得Am=0.若Am=0，且Am-1≠0，则称A为m次幂零变换，m称为A的冪零指数. 针对幂零变换我们有如下重要结论.

引理4.1 设A为线性空间V上的的m1次幂零变换.因此存在α1∈V，使得Am1-1(α1)≠0.设C(α1)为向量α相对A生成的循环子空间.

(i)α1,A(α1),…,Am1-1(α1)为C(α1)的一组基，且A|C(α1)在基α1，A(α1),…,Am1-1(α1)为C(α1)下的矩阵为

(1)

(ii) 存在A的不变子空间V1，使得V=C(α1)⊕V1，且A|V1也是幂零变换，且冪零指数小于等于m1.

证明见教材[1]例4.5.7.

在引理4.1(ii)中，幂零变换A|V1的幂零指数m2≤m1.再用引理4.1可知，存在α2∈V1,使得α2,A(α2),…,Am2-1(α2)为C(α2)的一组基，A|C(α2)在该基下的矩阵也形如矩阵(1)，且存在A的不变子空间V2，使得

V1=C(α2)⊕V2.

再考虑A|V2，得到V2=C(α3)⊕V3，依次进行分解. 因为V是有限维的，所以必存在α1,α2,…,αk，使得

V=C(α1)⊕C(α2)⊕…⊕C(αk).

这样就将V分解成若干个冪零变换的循环子空间的直和，且A在基

α1,A(α1),…,Am1-1(α1),…,αk,A(αk),…,Amk-1(αk)

下的矩阵为

(J(0,m1),J(0,m2),…,J(0,mk)).

5 根子空间与空间第一分解定理

数学中，从不同角度理解一个概念往往会得到很多意想不到的结果，有时只需要作一个简单的变形.

回到线性变换最理想的情况，即可对角化线性变换. 线性变换A可对角化的一个等价条件是

V=Vλ1⊕Vλ2⊕…⊕Vλs,

其中Vλi为A的属于特征值λi的特征子空间，λ1,λ2,…,λs为A的所有两两不同的特征值. 对于一般的线性变换，只有“直和”，未必有“等号”，即

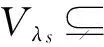
(2)

原因可以理解为某个或某几个特征子空间“不够大”. 于是一个自然的想法就是将这些“小了”的特征子空间扩大为另一个较大的不变子空间，即所谓的根子空间，使得(2)式不仅还是直和，而且等号成立. 这里需要下面的引理.

引理5.1 设A为线性空间V上一个线性变换，则

KerA⊂KerA2⊂…⊂KerAk⊂…

且存在k，使得KerAk=KerAk+1=KerAk+2=….

如果换个角度来看特征子空间，即Vλ0=Ker(A-λ0Z)，其中λ0为A的特征值，Z为V上的恒等变换.则不难想到可将特征子空间按照引理5.1的方式来扩大，即考虑Ker(A-λ0Z)k，其中k为一充分大的正整数，记为Wλi，称为A的属于特征值λ0的根子空间.

为什么能这样做？首先，因为(A-λ0Z)k是A的多项式，所以Wλ0=Ker(A-λ0Z)k一定是A的不变子空间；

其次，对每个Wλi, (A-λiZ)|Wλi=A|Wλi-λiZWλi都是幂零变换，正好可以利用上述对幂零变换的讨论结果；

最后，可以验证Wλ1+Wλ2+…+Wλs的确是直和，且等于V.

定理5.2(空间第一分解定理) 设A为复线性空间V上的线性变换，λ1,…,λs为A的所有两两不同特征值，则

V=Wλ1⊕…⊕Wλs,

其中Wλi为A的属于特征值λi的根子空间，i=1,…,s.

6 循环子空间与空间第二分解定理

有了空间第一分解定理，只需讨论线性变换A在每个根子空间Wλ0上的限制即可. 注意到，A|Wλ0=(A-λ0Z)|Wλ0+λ0ZWλ0,其中Wλ0上的线性变换(A-λ0Z)|Wλ0恰为一个幂零变换, 而λ0ZWλ0为一个数乘变换. 于是可以利用前文对幂零变换的讨论，直接给出如下结果.

定理6.1(空间第二分解定理) 设Wλ0为线性变换A属于特征值λ0的根子空间， 则存在向量α1,…,αk，使得

Wλ0=C(α1)⊕C(α2)⊕…⊕C(αk),

其中C(αi)为由αi生成的相对A|Wα0-λ0ZWλ0的循环子空间，i=1,…,k.

上述分解中，按照引理4.1(i)，可以选取循环子空间C(αi)的基

αi, (A-λ0Z)(αi),…,(A-λ0Z)mi-1(αi)，

其中mi为(A-λ0Z)|C(αi)的幂零指数，即满足(A-λ0Z)mi(αi)=0，但(A-λ0Z)mi-1(αi)≠0.将所有这些向量拼成Wλ0的一组基

α1(A-λ0Z)(αi)…,(A-λ0Z)mi-1(α1)，

…,

αk(A-λ0Z)(αi)…,(A-λ0Z)mk-1(αk)，

则A|Wλ0在该基下的矩阵为

diag(J(λ0,m1),…,J(λ0,mk)).

7 Jordan标准形存在性定理

综合空间第一、二分解定理, 线性空间V有如下直和分解

V=Wλ1⊕…⊕Wλs

=C(α11)⊕…⊕C(α1k1)⊕…⊕C(αs1)⊕…⊕C(αsks),

其中C(αij)为αij相对于A-λiZ生成的循环空间.设(A-λiZ)|C(αij)的幂零指数为mij，则A在V的基

α11,(A-λ1Z)(α11),…,(A-λ1Z)m11-1(α11)

…,

α1k1,(A-λ1Z)(α1k1),…,(A-λ1Z)m1k1-1(α1k1)

…,

αs1,(A-λsZ)(αs1),…,(A-λsZ)ms1-1(αs1)

…,

αsks,(A-λsZ)(αsks),…,(A-λsZ)msks-1(αsks)

下的矩阵为

diag(J(λ1,m11),…,J(λ1,m1k1)，…，J(λs,ms1)，…，J(λs,msks)).

最后，给出从Jordan标准形中直接读出的不变量.若

mi1≥…≥miki≥1,i=1,…,s.

则

(i)A的全部特征值为λ1,…,λs；

(v)特征值λi的几何重数为ki.

[1] 杜先能，叶郁，殷晓斌，范益政. 高等代数[M]. 北京：高等教育出版社，2013.

[2] 李炯生，查建国. 线性代数[M]. 合肥：中国科学技术大学出版社，2005.

[3] 李尚志，线性代数(数学专业用)[M]. 北京：高等教育出版社，2006.

[4] 全洪正，黄小英. 求矩阵Jordan标准形的一种新法[J]. 大学数学，2014，30(1)：107-113.

[5] 易福侠，王金林. 矩阵若当标准化的一种新方法[J]. 大学数学，2009，25(3)：164-167.

[6] Sergeichuk V V. Canonical matrices for basic matrix problems [J]. Linear algebra and its applications, 2000，317(1/3)：53-102.

[7] 刘学质. Jordan标准形过渡矩阵求法的补充条件[J]. 大学数学，2007，23(4)：148-151.

[8] 刘合国，徐涛. Jordan标准形定理的一个矩阵证明[J]. 湖北大学学报，2011，33(4)：437-443.

The Difficulty Decomposition of Analytic Method of Jordan Canonical Form Theory

BAOYan-Hong

(School of Mathematical Sciences, Anhui University, Hefei 230601, China)

Jordan canonical form theory plays an important role in linear algebras. However, it is a teaching difficulty to show the existence of Jordan canonical form theory by using analytic method. Combining with the teaching practice, the difficulties are decomposed by analysing the mathematical idea and technique of analytic method of Jordan canonical form theory.

Jordan canonical form; invariant subspace; root subspace; cyclic subspace

2016-01-16； [修改日期]2016-06-08

安徽省教育厅教学改革与质量提升计划(2014zdjy022)，安徽大学研究性教学示范课程项目(J10118443005)

鲍炎红(1981-),男，博士，副教授，从事代数表示论研究.Email:baoyh@ahu.edu.cn.

O151.21

C

1672-1454(2016)05-0096-05