浅析数学物理方程求解中的延拓思想——以波动方程为例

苏新卫

(中国矿业大学(北京)理学院数学系,北京100083)



浅析数学物理方程求解中的延拓思想
——以波动方程为例

苏新卫

(中国矿业大学(北京)理学院数学系,北京100083)

应用延拓方法和无界波动方程定解问题的达朗贝尔公式，求解半无界波动方程的定解问题，其中的边界条件分别为第一类和第二类非齐次型.旨在拓宽学生的解题思路，使学生灵活掌握解题方法，并为《数学物理方程》课程的教学提供些许参考.

波动方程； 达朗贝尔公式； 齐次化； 延拓

1 引 言

在很多有关数学物理方程的教材和偏微分方程求解的文献中[1-8]，对三大类数学物理方程—波动方程、热传导方程和泊松方程的几种重要求解方法作了详尽的描述.其中，行波法主要用来求解无界波动方程的初值问题.

首先，对于一维的问题

(1)

利用代换ξ=x+at,η=x-at将方程化简为标准型uξη=0，从而得到方程的通解为

u(x,t)=f1(x+at)+f2(x-at)，

(2)

进而应用初始条件得到上述问题(1)的解的公式—达朗贝尔公式

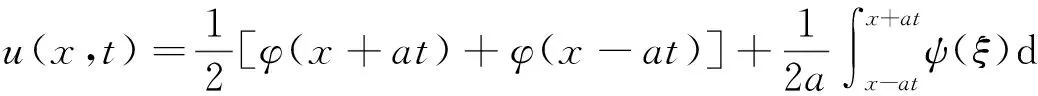
(3)

其次，应用公式(3)推导三维无界波动方程初值问题解的公式——泊松公式.最后，由泊松公式和降维法，得到二维无界波动方程初值问题的求解公式.因此，问题(1)的求解即公式(3)在用行波法求解无界波动方程的定解问题中起着至关重要的作用.为了加深对问题(1)及其求解公式(3)的理解和应用，在有关的教材中[1-3]，利用奇延拓的方法求解了带有齐次边界条件的半无界问题

(4)

数学中的延拓法，即在保持问题本身不变的条件下，拓展到更广的范围内讨论问题，其应用的广泛性是不言而喻的.就求解数学物理方程的定解问题而言，除上述在行波法中可以应用之外，在用积分变化法求解时，也可将有界或半无界问题延拓成无界问题再求解.在有关教材内容安排上，问题(4)的求解无疑可以启示学生用延拓法求解某些数学物理方程的定解问题，但仅此一例，对初学者来说稍有欠缺.

本文以半无界波动方程定解问题为例，具体说明延拓法在解数学物理方程定解问题中的应用，旨在拓宽学生的解题思路，使学生灵活掌握解题方法，并为《数学物理方程》课程的教学提供些许参考.不同于问题(4)，本文讨论的问题分别具有第一和第二类非齐次边界条件，从而更具一般性，应用更广.

2 第二类非齐次边界条件的半无界问题

本部分求解问题

(5)

2.1 分析问题

在问题(4)的求解中，边界条件齐次性是将函数φ(x),ψ(x)奇延拓，从而可以应用公式(3)求解的关键所在.而在问题(5)中，g(t)≠0，最简单常用的奇延拓方法失效，应该将函数φ(x),ψ(x)如何延拓呢？ 假设延拓后问题为

(6)

其中函数Φ(x)=φ(x),Ψ(x)=ψ(x),x≥0.由(3)可知(6)的解为

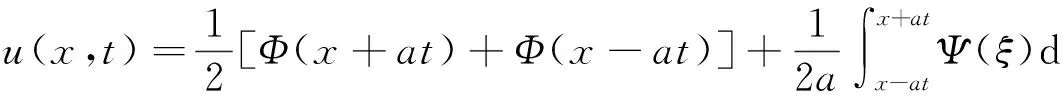
将(6)中边界条件代入上式得

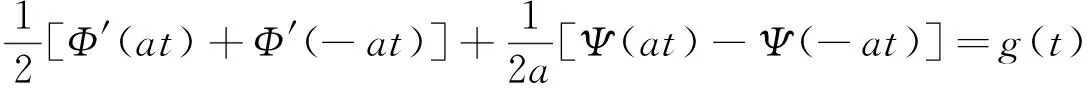
由此很难确定当x<0时函数Φ(x),Ψ(x)的定义.

2.2 边界条件齐次化

显然，为应用延拓方法，应先将问题(5)进行处理.注意到第一类齐次边界条件可奇延拓，不妨先将(5)边界条件齐次化.引入辅助函数w(x,t)满足wx(0,t)=g(t)，令v(x,t)=u(x,t)-w(x,t),则问题(5)化为

(7)

为求解(7)方便，让辅助函数同时满足wtt(x,t)=a2wxx(x,t),wx(0,t)=g(t).由(2)可知我们在函数类f1(x+at)+f2(x-at)中找一个满足wx(0,t)=g(t)的函数即可.不妨令f2(x-at)=0，即

w(x,t)=f1(x+at), wx(0,t)=g(t).

(8)

易知(8)的一个解为

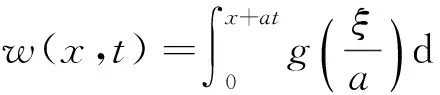
(9)

将(9)代入(7)可得

(10)

具有齐次边界条件的问题(10)就可以延拓了.

2.3 齐次边界条件问题的解

设将问题(10)延拓成无界问题

(11)

由达朗贝尔公式(3)和(11)中的边界条件可得

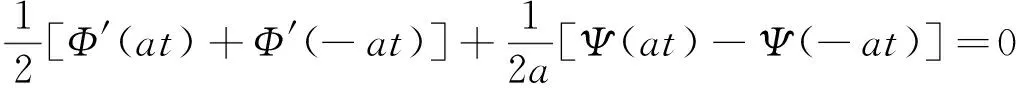
由此易知函数Φ和Ψ应该是偶函数，即(11)是将问题(10)进行的偶延拓， 因此

(12)

由(3)可知(11)的解为

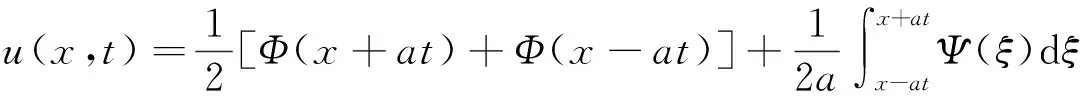
其中函数Φ和Ψ如(12)式定义.将解函数u(x,t)中的变量x限制到x≥0上，从而可得半无界问题(10)的解为

最后，得到问题(5)的解为u(x,t)=w(x,t)+v(x,t)，即

3 第一类非齐次边界条件的半无界问题

对于第一类非齐次边界条件问题

4 结 语

本文用延拓法求解了具有非齐次边界条件的半无界波动方程的定解问题，是对教材有关内容的补充和深入推广.为方便问题的求解，在阐释延拓法重要性的同时，展现了边界条件齐次化技巧.延拓法不仅可以用来求解半无界问题，有些有界问题，用延拓法也可以求解.例如对于x∈[0,l]上的波动方程的定解(混合、初边值)问题，可以先将问题延拓到x∈[-l,l]上，然后再进行周期延拓到x∈上成为无界问题，无界问题的解在x∈[0,l]上的限制既是原问题的解.当然，对于有些问题用延拓法求解未必方便简单.因此，在求解数学物理方程时应根据问题本身灵活选用不同的方法.

[1] 梁昆淼.数学物理方法[M]. 3版. 北京：高等教育出版社，2010.

[2] 谷超豪，等.数学物理方程[M]. 3版. 北京: 高等教育出版社，2012.

[3] 季孝达，等.数学物理方程[M]. 2版. 北京: 科学教育出版社，2009.

[4] 王元明.数学物理方程与特殊函数[M]. 3版. 北京：高等教育出版社，2004.

[5] 王志军,郭城.非线性波动方程的各向异性有限元方法[J].大学数学，2011，27(3): 150-152.

[6] 齐远节,刘利斌.求解二阶波动方程的三次样条差分方法[J].大学数学，2011, 27(1): 59-64.

[7] Pikulin V, Pohozaev S. Equations in Mathematical Physics [M]. New York: Springer, 2001.

[8] Kirkwood J. Mathematical Physics with Partial Differential Equations[M]. Amsterdam: Elsevier, 2013.

Analysis on the Extension Method of Solving Mathematical Physics Equations

SUXin-wei

(Department of Mathematics, School of Science, China University of Mining and Technology, Beijing 100083,China)

Applying the extension method and D′Alembert formula about the unbounded problem of wave equations, we solve the wave equations on semi-infinite interval, in which the boundary conditions are non-homogeneous types of the first and the second class respectively. The aims of this paper are to broaden the students′ problem-solving ideas and enable students to master the problem-solving methods. We expect that this paper can offer some advice for the teaching of mathematical physics equations.

wave equation; D’Alembert formula; homogenization; extension

2016-04-29； [修改日期]2016-06-15

中国矿业大学(北京)课程建设与教改项目(K150702)；国家自然科学基金项目(11371364)

苏新卫(1971—)，女，硕士，副教授，从事微分方程定性理论研究.Email:kuangdasuxinwei@163.com.

O175.24

C

1672-1454(2016)05-0092-04