条件分布计算的几个问题研究
宁荣健,周 玲
(合肥工业大学数学学院,合肥230009)
条件分布计算的几个问题研究
宁荣健,周 玲
(合肥工业大学数学学院,合肥230009)
主要通过举例,介绍二维连续型随机变量(X,Y)当fY(y)=0或fX(x)=0时相应的条件分布的几种情况.其结论表明条件分布可能是连续型分布,也可能是离散型分布,甚至还可能是非连续型非离散型分布,以此加深对条件分布的认识.
二维连续型随机变量; 条件分布; 条件密度函数; 条件分布函数
1 问题的提出
在诸多概率论与数理统计教材中,关于二维连续型随机变量(X,Y)的条件分布的概念描述为
设二维连续型随机变量(X,Y)的密度函数为f(x,y),如果已知Y的取值为Y=y,且fY(y)>0,就称
为在条件Y=y下X的条件密度函数.
同理,如果已知X的取值为X=x,且fX(x)>0,就称
为在条件X=x下Y的条件密度函数.
问题是,当Y=y时,如果fY(y)=0,那么在条件Y=y下,X的条件分布可能会怎么样?同理,当X=x时,如果fX(x)=0,在条件X=x下,Y的条件分布也可能会怎么样?
对此问题,教材中并没有作进一步描述.因此,有人认为上述条件分布不存在,这是不正确的.
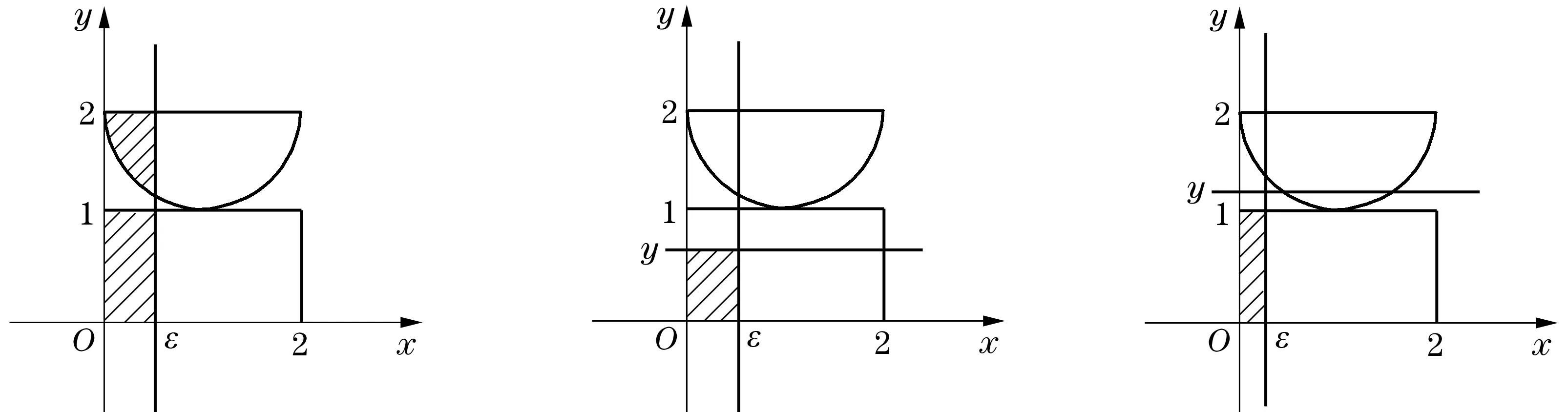
事实上,当Y=y或X=x时,尽管有fY(y)=0或fX(x)=0,但此时的条件分布也可能存在,除非条件Y=y或X=x不成立.例如,设随机变量(X,Y)在区域D:0 本文通过举例介绍当fY(y)=0或fX(x)=0时条件分布的几种情况,以丰富对条件分布的认识. 1.当fY(y)=0或fX(x)=0时,条件分布可能为连续型的分布 例1 设随机变量(X,Y)的密度函数为 求在X=0条件下Y的条件分布. 解 计算得 由于f(x,y)=fX(x)fY(y),所以X和Y相互独立,其条件分布就是其无条件分布,故在X=0条件下Y的条件密度为 例2 设随机变量(X,Y)的密度函数为 求在X=0条件下Y的条件分布. 解 对任意的ε(0<ε<1),有 当-∞ 图1 图2 当1≤y<+∞时,有P{Y≤y,-ε 综上可得 由此可知,此条件分布为[-1,1]上的均匀分布,其条件密度函数为 显然,例1和例2中相应的条件分布都是连续型的分布.需要指出的是,例1也可以利用条件分布函数求出Y的条件密度函数,其结果完全一样. 2.当fY(y)=0或fX(x)=0时,条件分布可能为离散型的分布 例3 设平面区域 随机变量(X,Y)在区域D上服从均匀分布,求在X=0条件下Y的条件分布. 故也不能按照 解 对任意的ε(0<ε<1),由几何概型计算得 当-∞ 当1≤y<+∞时,有P{Y≤y,-ε 综上可得 图3 图4 图5 图6 由此可得出,当X=0时,Y的条件分布是离散型的分布.且其条件分布律为 3.当fY(y)=0或fX(x)=0时,条件分布可能为非离散型,也非连续型的分布 例4 设随机变量(X,Y)的密度函数为 求在X=0条件下Y的条件分布. 解 对任意的ε(0<ε<1),计算得 由于 所以当ε→0+时, 当-∞ 所以 图7 图8 图9 当2≤y<+∞时,有P{Y≤y,-ε 综上可得 由此发现,该例中,当X=0时Y的条件分布既不是离散型,也不是连续型的分布. 条件分布是概率论与数理统计、随机过程等分支的重要内容之一.本文通过实例,分析和介绍了基于二维连续型随机变量的联合分布求边缘分布的常见方法和相关类型,供读者交流和参考.对于二维非连续型非离散型随机变量,其边缘分布也有类似的问题.由于内容比较复杂,此处不再多述. [1] 陈希孺.概率论与数理统计[M].合肥:中国科学技术大学出版社,1992:73-78. [2] 茆诗松,等.概率论与数理统计教程[M].北京:高等教育出版社,2007:185-192. [3] 盛骤,等.概率论与数理统计[M].北京:高等教育出版社,2010:90-110. [4] 杜雪樵,凌能祥,等.概率论与数理统计[M].合肥:合肥工业大学出版社,2009:110-130. Study on Several Problems of Conditional Distribution Calculation NINGRong-jian,ZHOU-ling (School of Mathematics, Hefei University of Technology, Hefei 230009, China) The paper introduces several cases of two-dimensional continuous random variable (X,Y)’s conditional distribution when fY(y)=0 or fX(x)=0 through examples. The conclusion shows that conditional distribution may be continuous distribution, may also be a discrete distribution, it may even be non continuous non discrete distribution.We may deepen the understanding of conditional distributions by it. two dimensional continuous random variable; conditional distribution; conditional density function; conditional distribution function 2015-10-12; [修改日期] 2016-06-12 合肥工业大学教学改革研究项目(重点项目) YJG2015Z01 宁荣健(1962-),男,副教授,从事计算数学研究. Email:nrjian@126.com 周玲(1970-),女,副教授,从事概率统计方面研究.Email:hfdxsx@163.com O211.3 C 1672-1454(2016)05-0061-062 主要举例

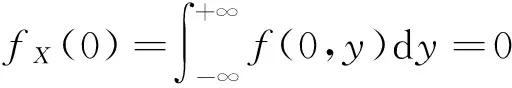

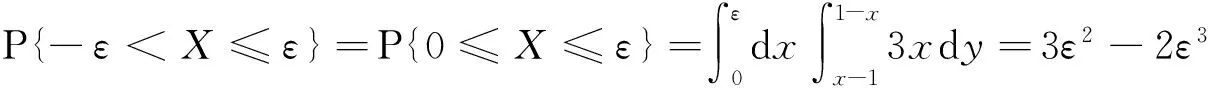
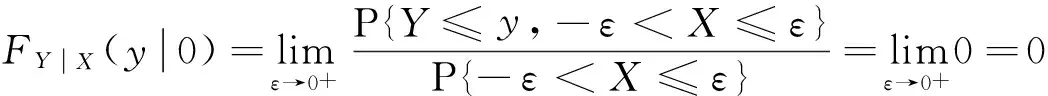
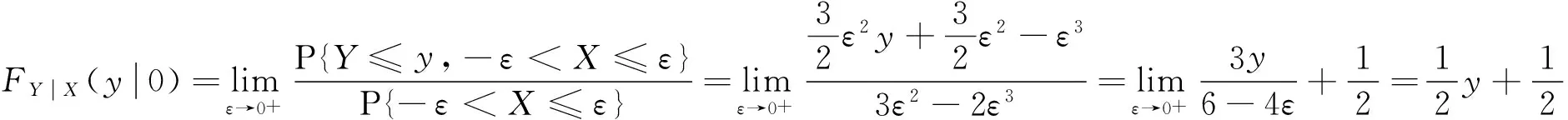

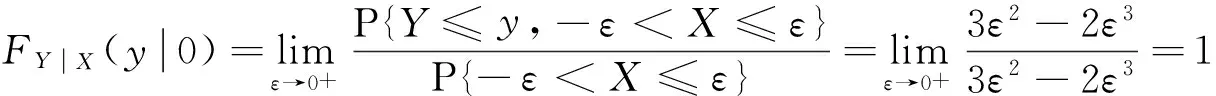
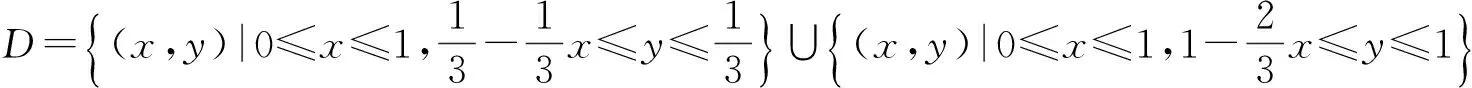
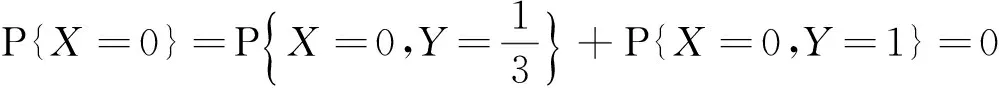
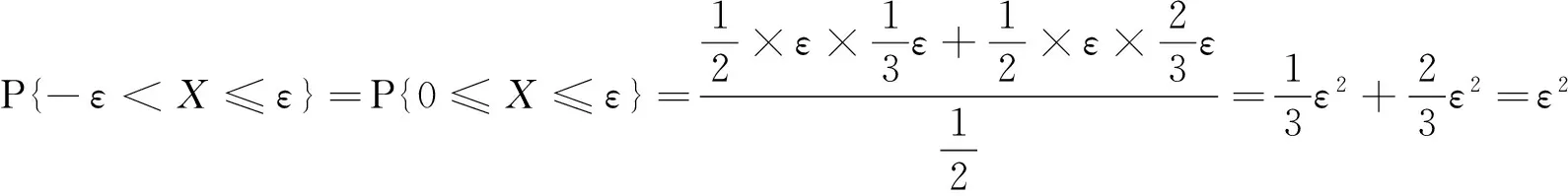
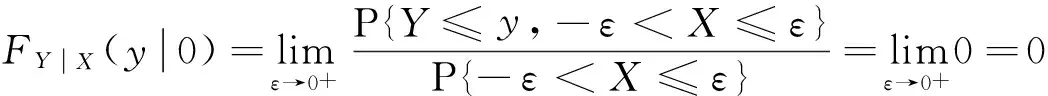

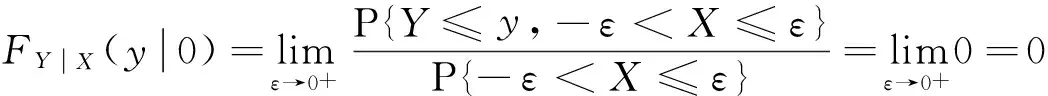

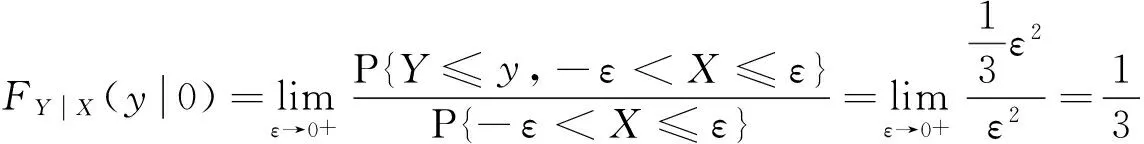
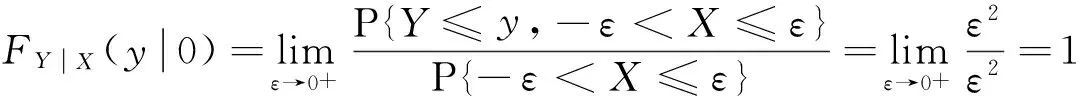

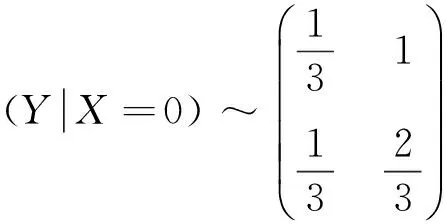
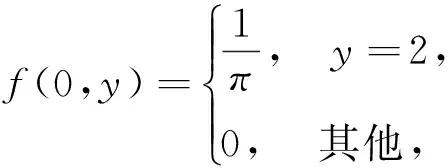
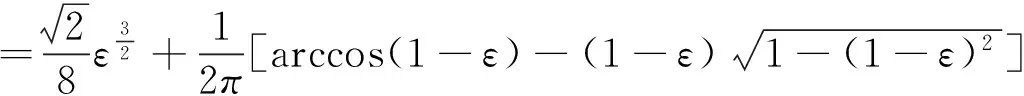
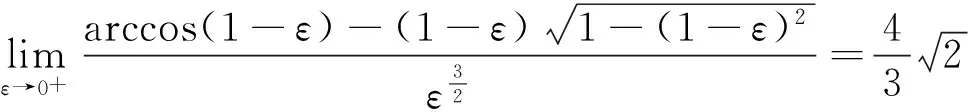

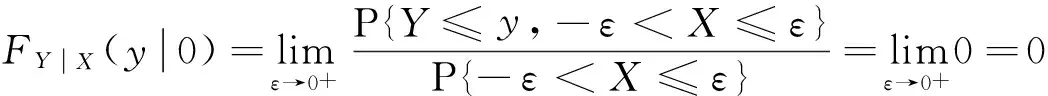
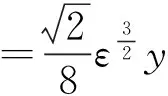
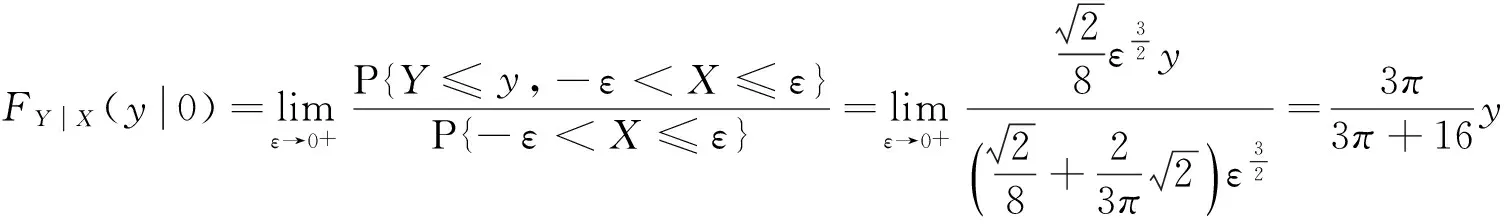
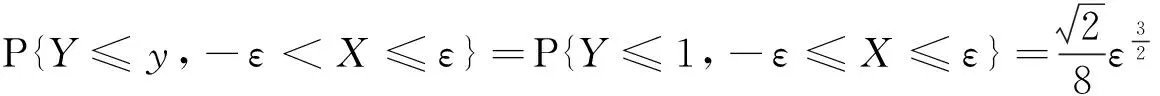
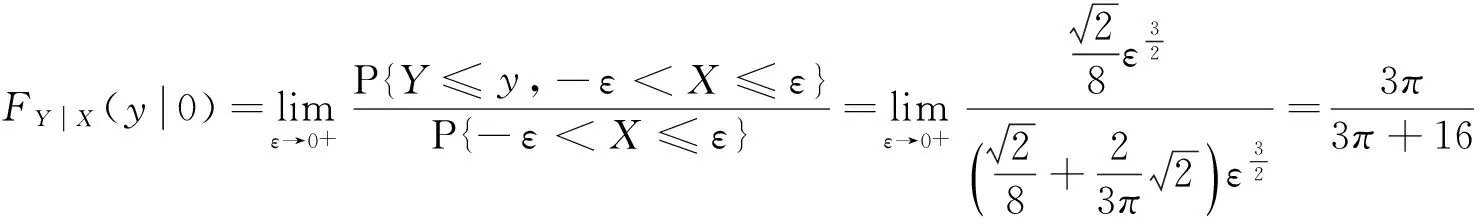
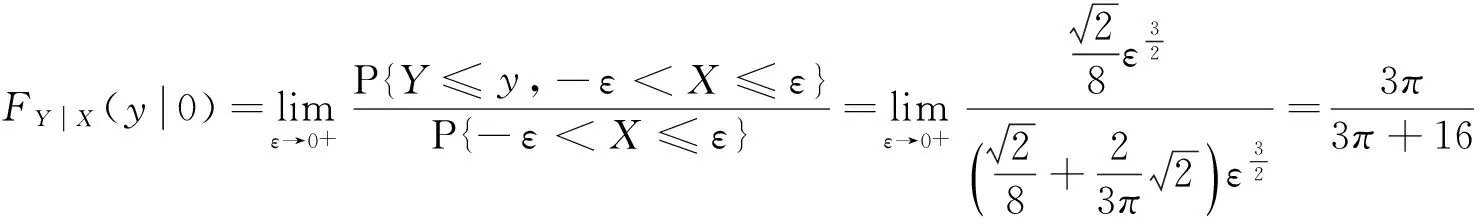

3 结束语

