土坡悬臂式抗滑桩一种抗震设计计算方法*
肖世国 祝光岑
XIAO Shiguo①② ZHU Guangcen③
土坡悬臂式抗滑桩一种抗震设计计算方法*
肖世国①②祝光岑③

在强震动力作用下,边坡常会产生较大的永久位移,且抗滑桩锚固段顶端前侧局部地层易进入塑性屈服状态,这在传统的悬臂式抗滑桩抗震设计计算中没有给予充分考虑。基于Nemark滑块位移法和极限分析原理,提出了考虑边坡设计安全系数和地震永久位移的作用于抗滑桩上设计滑坡推力的计算方法; 同时,根据锚固段地层进入塑性屈服状态的情况提出把锚固段分为塑性区锚固段和弹性区锚固段分别计算,前者按极限地层反力法采用悬臂梁模型计算,后者按照弹性地基梁模型计算,在两者界面处需满足桩体内力和变形以及地层反力的连续条件。结合一土质边坡工程算例,给出了所提出的悬臂式抗滑桩抗震设计三段分析法的具体计算过程和结果,进一步表明所提出的方法具有技术合理性和经济性。
土质边坡 抗滑桩 抗震设计 永久位移 塑性区锚固段
XIAO Shiguo①②ZHU Guangcen③

0 引 言
目前,悬臂桩法、地基系数法、p-y曲线法、有限元法等是普通抗滑桩内力计算分析的主要方法(Stecen et al.,1979; Dunnawant et al.,1989; Dawson et al.,1999; Griffiths et al.,1999; 戴自航等, 2003; 李海光等, 2004; 郑颖人等, 2004; 胡晓军等, 2010)。在静力条件下,传统的边坡抗滑桩加固工程设计通常仅考虑抗滑桩的强度要求(铁道部第二勘测设计院, 1983; 周德培等, 2004; 郑颖人等, 2007),以强度设计安全系数作为主要设计控制指标,而不考虑加固后的坡体位移条件。然而,在地震动力条件下,虽然抗滑桩的有限元强度折减法设计计算也有所应用(叶海林等, 2010),有一定的实际参考意义,但其主要依赖于数值模型,操作过程有时存在一定的主观性且较为繁琐,尤其是只考虑强度条件控制的设计方法未必合理。如: 5·12 汶川地震震害调查结果表明(李乔等, 2008; 肖世国等, 2011),某些道路边坡尽管采用抗滑桩加固,但在地震影响下边坡抗滑桩仍产生了较大的歪斜变形,存在一定的安全隐患。
普通抗滑桩在设计计算时,其地层反力通常被限制于弹性范围之内。然而,当锚固段地层塑性区长度不超过该段总长的 1/4~1/5时,地层通常并不会破坏(赵肃菖等, 2003)。因此,传统的弹性设计方法偏保守,特别在地震力作用下,其缺陷尤甚。
以往研究中曾提出了静力条件下抗滑桩的弹塑性设计模式(陈立新等, 1997; 王士川等, 1997; 周春梅等, 2008),对地层建立了楔形体破坏模式,给出了地层弹塑性区临界高度算法,对实际工程有一定的参考意义。但采用此方法确定的临界高度,假定弹塑性平衡区是底面为平面的空间楔形体,采用了较多的近似简化,在具体工程应用时仍有局限性。
鉴于以往研究的相关问题,本文考虑采用强度安全系数和边坡永久位移相结合的方式,并考虑抗滑桩锚固段地层的塑性变形和屈服问题,对土质边坡抗滑桩的抗震设计方法进行讨论,以建立一种新的抗滑桩抗震设计计算方法,为工程实践中更合理加固高烈度地区的边坡提供理论参考。
1 分析方法
1.1 设计滑坡推力与边坡永久位移的关系
对于加固边坡的抗滑桩,在某设计安全系数下,作用于受荷段桩后侧压力与桩前侧压力合力之差即为作用于抗滑桩上的设计滑坡推力。可将其简化为作用于滑面处的一水平力和力矩,根据极限分析原理,则其对滑体所做功率可以确定,进而由极限分析上限定理可定义坡体的设计安全系数,从而可导出在地震作用下设计滑坡推力与相应的设计安全系数Fs之间的关系。
(1)
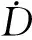
关于屈服加速度的确定,可分两种情况:(1)对滑面已知的土坡,可根据设计边坡推力计算; (2)对于滑面未知的土坡,以产生最小屈服加速度的滑面作为设计滑面来计算确定。
根据Newmark的滑块位移法(Newmark, 1965),将刚性滑体产生的所有瞬时位移累加得到其永久位移,这里以抗滑桩与滑面交点处的水平位移作为计算量。若令地震加速度系数k=a/g,a和g分为地震和重力加速度;kc为屈服加速度系数(屈服加速度/重力加速度); 则仅当k>kc时,坡体产生瞬时滑动变形,并产生速度和位移。因此,地震边坡永久位移u即为g(k-kc)在地震全持时T范围内对时间t的二次积分。
u=C∫T∫Tg(k-kc)dtdt
(2)
式中,C为与滑体重度及滑体几何形态有关的积分计算系数。
上述相关公式推导,具体参见文献(肖世国等, 2013)。这样,通过边坡的地震屈服加速度即可建立起设计滑坡推力与坡体永久位移之间的关系。于是,若边坡工程抗震设计中在某安全系数下又限定了加固边坡的地震永久位移,则可以反算确定作用于抗滑桩上的设计滑坡推力。具体可通过电算实现,这里不再赘述。

图1 抗滑桩分段计算模型
1.2 锚固段地层塑性区高度的确定
(1)假定桩体锚固段地层为理想弹塑性体,当其所受水平向应力大于地层侧向容许承载力[σ]时,其即进入塑性屈服状态。
(2)按弹性地基梁法对桩锚固段进行试算,比较计算得到的地层水平向应力与[σ],则大于[σ]的区段为塑性区,将此段的地层抗力均调为[σ],重算锚固段的地层水平向应力。
(3)重复(2)的操作,直到弹塑性地层界面上的水平应力等于[σ]为止。
1.3 抗滑桩的内力计算
1.3.1 受荷段
在根据1.1节的方法计算确定出设计滑坡推力后,在地震作用下的滑坡推力分布模式,近似按矩形分布处理。将抗滑桩受荷段看作滑面处固定的悬臂梁进行计算,可以得到桩身内力及变形。
1.3.2 塑性区锚固段
由1.2节阐述,可得图1 所示的抗滑桩在地震作用下的简化受力模式,抗滑桩分为3段计算,从上而下依次为受荷段(即滑面以上部分,高度为h1)、塑性区锚固段(简称塑性段,高度为h2)、弹性区锚固段(简称弹性段,高度为h3)。其中滑面以下的塑性区锚固段(地层达到塑性极限状态),桩侧地层水平抗力q1为[σ],桩体受荷段底端作用有剪力Q1和弯矩M1。因而,仍可按悬臂梁模型计算该段桩内力,该段桩体内力和位移表达式为:

(3)
式中,yx、φx、Mx、Qx为塑性区锚固段桩身任意截面的位移(m)、转角(°)、弯矩(kN·m)和剪力(kN); σx为塑性区锚固段地层抗力(kPa); y0,φ0为弹性区锚固段顶面处的桩身水平位移(m)、转角(°); x为计算点到塑性区锚固段顶端距离(m); h2为塑性区锚固段桩体长度(m)。
由静力平衡条件,可得在弹、塑性区锚固段界面处抗滑桩的剪力Q0和弯矩M0。
(4)
1.3.3 弹性区锚固段
根据锚固段不同地层特征,弹性区锚固段内力可根据弹性地基梁理论采用地基系数法求解,详见文献(铁道部第二勘测设计院, 1983),这里不再赘述。然而,需要注意的是,弹性区锚固段顶端的内力应与塑性区锚固段的底端内力一致,且弹性区锚固段顶端地层侧向抗力为地层横向容许承载力,需要以此作为附加条件进行弹、塑性区锚固段的内力计算,其间需要经过有限次的迭代试算。其主要计算流程(图2),其中,塑性区锚固段深度h2可从零开始逐渐增大取值试算。

图2 弹、塑性区锚固段计算流程
2 计算步骤
考虑设计安全系数和边坡永久位移共同控制,并兼顾考虑锚固段地层塑性屈服的抗滑桩弹塑性抗震设计计算方法,主要步骤为:
(1)根据坡体地层条件合理确定桩位;
(2)考虑设计安全系数、峰值加速度和永久位移等主要因素,合理计算边坡设计推力,并确定其分布模式,一般可考虑近似采用矩形分布;
(3)对抗滑桩分受荷段、塑性区锚固段、弹性区锚固段共3段进行计算;
(4)采用悬臂梁模型计算抗滑桩受荷段的内力和变形;
(5)根据弹性地基梁理论,采用试算法计算锚固段地层的塑性区深度;
(6)分别计算塑性区、弹性区锚固段的桩体内力和变形,将3段的内力和位移分别叠加。

图3 某工程边坡算例
3 算例分析与讨论
如图3所示的某工程边坡,滑床为强风化泥岩,饱和单轴抗压强度为8MPa,横向容许承载力[σ]取为1.0MPa,地基水平抗力系数为1.5×105kN·m-3,其上覆粉质黏土,重度γ=20kN·m-3,内摩擦角φ=23°,黏聚力c=18kPa。边坡高度为16m,坡顶面倾角为0°,坡面倾角为35°,坡顶面处滑面距坡顶前缘约10.8m。边坡采用抗滑桩加固,桩体为C30混凝土,桩长16m,其中锚固段长8m,抗滑桩设置在距离坡脚(受荷段桩前土体全部挖除)11.4m的位置。取设计安全系数Fs=1.15。采用汶川地震波(卧龙台站东向)作为设计地震波(Xiao et al.,2010),抗滑桩与滑面交点处的设计水平永久位移限制取为10cm(取桩长的0.5%~1%)。
为便于利用1.1节所述的相关公式分析问题,采用曲线拟合方法,将滑面简化为对数螺旋面,如图3 中虚线所示,曲线方程为r=r0·exp[(θ-θ0)tanφ],其中,r0=20.4m,θ0=47°,θ变化区间为47°~105°。
根据已知设计参数,按照前述分析方法,可得到加桩后的边坡在地震作用下的屈服加速度为0.42g,进而算得桩后设计水平滑坡推力为976kN·m-1。抗滑桩截面尺寸拟取为2.0m×3.0m,桩间距为5m。
桩后的坡体压力按矩形分布模式计算,可算得设计滑坡推力沿受荷段的线分布力为610kN·m-1。从而,计算可得受荷段的内力,并且可得到锚固段地层塑性区为滑面下0.96m深度范围内(距桩顶8~8.96m范围),对其进行应力调整后,按前面所述的方法即可计算出塑性区锚固段、弹性区锚固段的内力。全桩计算结果如图4 所示。
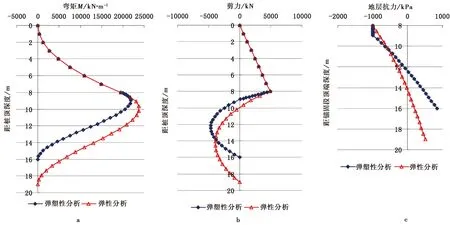
图4 桩身内力与地层反力
由图4可见,按前述的弹塑性分析法(锚固段分塑性区和弹性区)确定的桩身最大弯矩为21900.8kN·m,位于滑面下0.976m,最大剪力为4880kN,位于滑面处。若按以往的弹性设计方法,算得桩前地层最大抗力为1.7MPa,大于其横向容许承载力1.0MPa,需要调整桩体设计参数,此时,需将桩截面调整为2.5m×3.5m,且锚固段长度达到11m,方能满足地层横向容许承载力的要求,其内力与地层反力如图4 所示。可见,桩身最大弯矩为23790kN·m(滑面下2.2m处),最大剪力为4880kN(滑面处)。最大弯矩较采用本文方法计算的结果增大了8.6%,而最大剪力则相同。此外,由于桩体截面和锚固深度的增大,单桩的桩孔挖方量和混凝土用量均增加了70.25m3,明显增加了工程造价。因此,综合而言,对悬臂式抗滑桩加固的边坡抗震设计,采用弹塑性设计计算方法更为符合实际,且在一定程度上提高了经济效益。
4 结 语
在强震作用下,工程边坡可产生较大的永久位移,在边坡抗滑桩设计时除了要考虑强度控制条件外,还应考虑对这一变形参数的限制,即采用强度和变形共同控制设计的方法。边坡永久位移与屈服加速度有关,后者又与抗滑桩上的设计滑坡推力有关,因而限制永久位移即为限定了设计滑坡推力。在这种较大设计滑坡推力作用下,边坡抗滑桩(尤其土质或似土质边坡)锚固段桩前地层易出现塑性屈服区(尤其近滑面处),可以对锚固段分塑性区锚固段和弹性区锚固段分别计算,其中塑性区锚固段可采用地层横向容许承载力作为控制设计参数,通过极限地层反力法和弹性地基梁法计算(其间经过有限次迭代)得到塑性区锚固段和弹性区锚固段的内力和变形。于是,在这种抗滑桩弹塑性设计方法下,实际是将抗滑桩的计算分析分为受荷段(悬臂梁模型)、塑性区锚固段(悬臂梁模型)、弹性区锚固段(弹性地基梁模型)三段实现。
本文所提出的方法主要针对土质边坡或似土质边坡的抗滑桩抗震设计,较传统的弹性设计方法有明显的合理性和经济性。至于岩质边坡的抗滑桩抗震设计,可以在本文方法的基础上,进行进一步深入研究。
Chen L X,Wang S C. 1997. The analysis of elastic-plastic design theory of anti-slide piles[J]. Industrial Construction,27(7): 28~33.
Dai Z H,Shen P S,Peng Z B. 2003. Study on the finite difference method in calculation of internal forces of prestress-anchored antislide piles[J]. Chinese Journal of Rock Mechanics and Engineering,22(3): 407~413.
Dawson E M,Roth W H. 1999. Slope stability analysis by strength reduction[J]. Géotechnique,49(6): 835~840.
Dunnawant T W,O’Neill M W. 1989. Experimental p-y model for submerged stiff clay[J]. Journal of Geotechnical Engineering,115(1): 95~114.
Griffiths D V,Lane P A. 1999. Slope stability analysis by finite elements[J]. Géotechnique,49(3): 387~403.
Hu X J,Tan X H. 2010. Foundation counter force loading method for calculating internal forces of a whole elastic anti-sliding pile[J]. Rock and Soil Mechanics,31(1): 299~303.
Li H G,et al. 2004. Design method and practice of new-type earth retaining structures[M]. Beijng: China Communications Press.
Li Q,Zhao S C. 2008. Analysis of engineering damages caused by Wenchuan earthquake[M]. Chengdu: Southwest Jiaotong University Press.
Newmark N M. 1965. Effects of earthquakes on dams and embankments[J]. Géotechnique,15(2): 139~160.
Stecen J B M,Audibert J M E. 1979. Re-examination of p-y curve formations[C]∥Proc.11th Offshore Technology Conference, Houston, Texas, USA: [s.n.]: 397~403.
The Second Survey and Design Institute of Railway Ministry. 1983. Design and analysis of stabilizing piles[M]. Beijing: China Railway Press.
Wang S C,Chen L X,Zhang J. 1997. The rational analysis on the elastoplasticity of anti-slide piles(Ⅱ)[J]. Journal of Xi’an University of Architecture & Technology,29(4): 426~429.
Xiao S G,Feng W K,Zhang J J. 2010. Analysis of the effects of slope geometry on the dynamic response of a near-field mountain from the Wenchuan earthquake[J]. Journal of Mountain Science,7: 353~360.
Xiao S G,Zhang J J,Ma Y X. 2011. Investigation of failure of side-hill gravity retaining walls in regions of the Wenchuan earthquake[J]. Chinese Journal of Underground Space and Engineering,7(1): 174~178.
Xiao S G,Zhu G C. 2013. Seismic permanent displacement of clay slopes reinforced with cantilever stabilizing piles[J]. Rock and Soil Mechanics,34(5): 1345~1350.
Ye H L,Zheng Y R,Huang R Q,et al. 2010. Study of application of strength reduction dynamic analysis method to aseismic design of anti-slide piles for landslide[J]. Rock and Soil Mechanics, 31(S1): 317~323.
Zhao S C,Du Y T. 2003. Design method and practice in landslide control engineering[M]∥Proceeding of landslides(Volume sixteen).Beijing: China Railway Press: 21~22.
Zheng Y R,Chen Z Y. 2007. Slope and Landslide Engineering Control. Beijing: China Communications Press.
Zheng Y R,Zhao S Y. 2004. Calculation of inner force of support structure for landslide/slope by using strength reduction fem[J]. Chinese Journal of Rock Mechanics and Engineering,23(20): 3552~3558.
Zhou C M,Yin K L,Jian W X. 2008. Calculation of critical height of rock-soil elastoplastic area before anti-slide pile on declining sliding surface[J]. Rock and Soil Mechanics,29(7): 1949~1954.
Zhou D P,Xiao S G,Xia X. 2004. Discussion on rational spacing between adjacent anti-slide piles in some cutting slope projects[J]. Chinese Journal of Geotechnical Engineering,26(1): 132~135.
陈立新,王士川. 1997. 抗滑桩的弹塑性理论分析[J]. 工业建筑,27(7): 28~33.
戴自航,沈蒲生,彭振斌. 2003. 预应力锚固抗滑桩内力计算有限差分法研究[J]. 岩石力学与工程学报,22(3): 407~413.
胡晓军,谭晓惠. 2010. 弹性抗滑桩全桩内力计算的地基反力荷载法[J]. 岩土力学,31(1): 299~303.
李海光等. 2004. 新型支挡结构设计与工程实例[M]. 北京:人民交通出版社.
李乔,赵世春. 2008. 汶川大地震工程震害分析[M]. 成都:西南交通大学出版社.
铁道部第二勘测设计院. 1983. 抗滑桩设计与计算[M]. 北京:中国铁道出版社.
王士川,陈立新,张进. 1997. 抗滑桩的弹塑性理论分析(Ⅱ)[J]. 西安建筑科技大学学报,29(4): 426~429.
肖世国,张建经,马耀先. 2011. 汶川地震区路堑重力挡墙震害调查[J]. 地下空间与工程学报,7(1): 174~178.
肖世国,祝光岑. 2013. 臂式抗滑桩加固黏土边坡地震永久位移算法[J]. 岩土力学,34(5): 1345~1350.
叶海林,郑颖人,黄润秋,等. 2010. 强度折减动力分析法在滑坡抗滑桩抗震设计中的应用研究[J]. 岩土力学,31(增1): 317~323.
赵肃菖,杜寅堂. 2003. 滑坡整治工程设计思想与实践[M]. 滑坡文集(第十六集).北京:中国铁道出版社: 21~22.
郑颖人,陈祖煜. 2007. 边坡与滑坡工程治理[M]. 北京:人民交通出版社.
郑颖人,赵尚毅. 2004. 用有限元强度折减法求滑(边)坡支挡结构的内力[J]. 岩石力学与工程学报,23(20): 3552~3558.
周春梅,殷坤龙,简文星. 2008. 滑动面倾斜时抗滑桩弹塑性区临界高度的计算[J]. 岩土力学,29(7): 1949~1954.
周德培,肖世国,夏雄. 2004. 边坡工程中抗滑桩合理桩间距的探讨[J]. 岩土工程学报,26(1): 132~135.
JournalofEngineeringGeology工程地质学报 1004-9665/2016/24(5)- 01028- 09
A SEISMIC DESIGN METHOD FOR CANTILEVER-TYPE STABILIZING PILES IN SOIL SLOPE
Permanent displacement and plastic zone in the stable strata of a soil slope occur generally in the slope reinforced by stabilizing piles under the condition of intensive seismic action. However, the two important factors are usually omitted in the traditional aseismic design and analysis for slopes with cantilever-type stabilizing piles. Based on the principle of the rigid Newmark sliding model and limit analysis, the computational method is proposed that engineered landslide thrust on a stabilizing pile can be determined, by taking into consideration design safety factor and permanent displacement of the slope with piles. Meanwhile, according to the condition that some area in the stable strata of the slope is in the plastic state, the section of a stabilizing pile in the stable strata can be further divided into the segment in plastic zone of the strata and the segment in elastic zone of the strata. Therefore, the former can be regarded as cantilever beam model with uniformly lateral limit ground reaction; the latter can be analyzed by use of elastic foundation beam model. Their continuous conditions including internal forces and deformation of a pile and lateral ground reaction should be met at the interface between the two segments. The proposed method is demonstrated by a soil slope engineering example, in which calculation procedure and corresponding results are given in detail by the three section analysis method for the aseismic design of a cantilever-type stabilizing pile. The results show further that the proposed method is reasonable and cost effective.
Soil slope, Stabilizing pile, Aseismic design, Permanent displacement, Plastic zone in the stable strata of a slope
10.13544/j.cnki.jeg.2016.05.034
2016-05-20;
2016-07-20.
国家自然科学基金项目(51278430),新世纪优秀人才支持计划(NCET-13-0976)资助.
肖世国(1973-),男,博士,教授,博士生导师,主要从事边坡稳定性与支挡结构研究. Email: shgxiao3852@sina.com
TU443
A

